7.1 銷售趨勢分析
利用歷史銷售數據統計月銷售額,計算季節化因子,獲取去季節化銷售數據,然后進行線性擬合,最后預測接下來的某個月的銷售額。
第一步:讀數,統計月銷售額
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(orderDate,quantity,price,discount) |
| 2 | =A1.groups(month@y(orderDate):YMonth;sum(quantity*price*discount):Amount) |
A2 month@y(orderDate) 中選項@y表示返回的是yyyyMM這樣格式的數據
第二步:統計月銷售額的總均值
| A | |
|---|---|
| 3 | =A2.avg(Amount) |
第三步:計算去季節化因子
| A | |
|---|---|
| 4 | =A2.groups(YMonth%100:Month;avg(Amount)/A3:seasonal_factor).keys@i(Month) |
A4 YMonth%100 表示 YMonth 除以 100 的余數,這樣返回的就是 MM 這樣格式的整數,按這樣的月份數據分組匯總,可以分別統計 1 月的均值、2 月的均值……,用當前月份的均值除以 A3(總均值),即可獲得當前月份的季節因子。
keys@i(Month) 表示對當前序表設置主鍵字段和索引字段為 Month,方便后續按月份查找季節因子,效率更高。選項 @i 表示同時設置索引字段,如果無 @i 選項,則僅設置主鍵字段。
第四步:計算去季節化后的月銷售額
| A | |
|---|---|
| 5 | =A2.derive((YMonth\100-2020)*12+ YMonth%100:period_num,Amount/A4.find(YMonth%100).seasonal_factor:deseasonalized) |
A5 (YMonth\100-2020)*12+ YMonth%100表達式的含義:以 2020 年 1 月份為 1,之后月份遞增,從而獲得一個月份的自然數列,作為橫軸
Amount/A4.find(YMonth%100).seasonal_factor 表達式的含義:用當前月份的月銷售額除以當前月份的季節因子,返回值作為去季節化的銷售額。其中 A4.find(YMonth%100) 表示從 A4 序表中用其主鍵索引查找 YMonth%100 對應的記錄,因此 A4 必須事先建主鍵和索引。
A5 的運行結果:
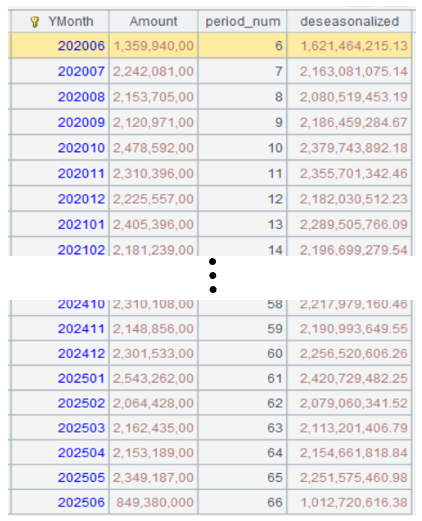
第五步:線性擬合
| A | |
|---|---|
| 6 | =linefit(A5.(period_num),A5.(deseasonalized)) |
A6 將 A5 中算得的月份的數列和對應月份的去季節化月銷售額進行線性擬合,其中 linefit 為線性擬合函數。本例中兩個參數均為一維的向量,因此對應的方程為:y=ax,函數中第一個參數為 x,第二個參數為 y,返回值為 x 的系數 a。
第六步:預測未來的月銷售額
| A | |
|---|---|
| 7 | =A6*67 |
| 8 | =A7*A4.find(67%12).seasonal_factor |
A7 從前面 A5 的運行結果可以看出,總數據是到 period_num 為 66,因此我們預測 67 的月銷售額,用 A6 乘以 67,即可得到 67 的去季節化銷售額。
A8 用 A7 中的去季節化銷售額乘以季節因子,就可以得到 67 對應的真正月銷售額。
知識點:linefit 函數
線性擬合(Linear Fitting)是一種通過線性模型(通常是一條直線)來近似描述數據集中變量之間關系的統計方法。它假設因變量(目標變量)與一個或多個自變量(特征變量)之間存在線性關系,并通過最小化誤差來找到最佳擬合的線性方程。
核心概念
1. 線性模型:
- 一元線性擬合(單變量):形式為 y=ax+b,其中:
- y 是因變量
- x 是自變量
- a 是斜率(回歸系數)
- b 是截距
- 多元線性擬合(多變量):形式為 y=a1x1+a2x2+?+b,適用于多個自變量的情況。
2. 目標:
- 找到參數(斜率和截距),使得模型預測值與實際數據點的誤差最小(通常使用最小二乘法)。
3. 最小二乘法:
- 通過最小化殘差平方和(預測值與真實值之差的平方和)來確定最佳擬合直線。
函數語法
linefit(A,Y) 用最小二乘做線性擬合,系數矩陣為A,常數Y
@1 當Y是向量時,返回向量而非矩陣
應用場景
- 預測房價與面積的關系。
- 分析廣告投入與銷售額的關聯。
- 實驗數據的趨勢分析。
優缺點
- 優點:簡單、計算高效、易于解釋。
- 缺點:對非線性關系擬合效果差,易受異常值影響。
7.2 銷售趨勢分析 2
上例僅對月份和銷售額做分析,實際應用中,銷售額和產品價格也會有很大的依賴關系,同時還會有系數的影響,即上例中提到的方程 y=ax+b 中的截距 b,本例就來分析銷售額和月份、產品價格之間的關系,對應的方程是 y=a1x1+a2x2+b,其中 x1代表月份,x2代表產品價格。
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(orderDate,quantity,price,discount) |
| 2 | =A1.groups(month@y(orderDate):YMonth,price;sum(quantity*price*discount):Amount) |
| 3 | =A2.avg(Amount) |
| 4 | =A2.groups(YMonth%100:Month,price;avg(Amount)/A3:seasonal_factor).keys@i(Month,price) |
| 5 | =A2.derive((YMonth\100-2020)*12+ YMonth%100:period_num, Amount/A4.find(YMonth%100,A2.price).seasonal_factor:deseasonalized) |
| 6 | =linefit@1(transpose([A5.(period_num),A5.(price),A5.(1)]),A5.(deseasonalized)) |
| 7 | =file(“product.csv”).import@tc(productID,listPrice) |
| 8 | =A7.derive((67*A6(1)+listPrice*A6(2)+A6(3))*A4.find(67%12,listPrice).seasonal_factor:Predicted) |
A2、A4 分組匯總時加上產品價格price字段,A4 的主鍵索引也加上 price 字段
A6 linefit 函數加上 @1 選項,表示返回值是個序列而非矩陣。參數transpose([A5.(period_num),A5.(price),A5.(1)])表示由period_num、price、數列1三個序列組成的矩陣,數列 1 表示截距 b*1。
A6 的運行結果:
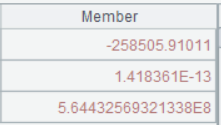
A7 從產品表讀取 productID,listPrice
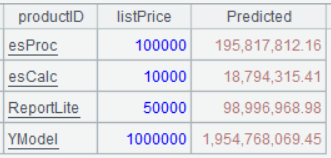
A8 預測下個月 (即月份期數為 67) 幾種不同價格產品的銷售額,其計算公式為 y=a1x1+a2x2+b,其中 a1、a2、b 分別對應 A6 返回的三個值,x1為月份期數,x2為產品列表價
A8 的運行結果:
7.3 銷售數量與折扣的相關性分析
銷售數量是否與折扣有關?訂貨量大折扣大嗎?相關性分析可以回答這些問題:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@ct(quantity,discount) |
| 2 | =pearson (A1.(discount),A1.(quantity)) |
A2 計算折扣與銷售數量之間的 Pearson 相關系數
知識點:pearson 函數
Pearson 相關系數(記作 r)是一種衡量兩個連續變量之間線性關系強度和方向的統計量,取值范圍為 [?1,1]。
核心概念
1. 定義:
- 衡量兩個變量 X 和 Y 的線性相關性。
- 計算公式:
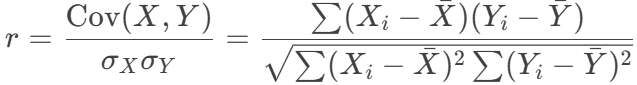
- 其中:
- Cov(X,Y) 是協方差
- σX,σY 是標準差
是均值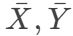
2. 取值范圍:
- r=1:完全正相關(變量呈嚴格遞增線性關系)
- r=?1:完全負相關(變量呈嚴格遞減線性關系)
- r=0:無線性相關性(但可能有非線性關系!)
3. 特點:
- 僅適用于線性關系,無法捕捉非線性關聯(如 y=x2y=x2)。
- 對異常值敏感,極端值可能顯著影響 rr。
- 取值范圍在 [?1,1][?1,1],絕對值越大,相關性越強。
函數語法
pearson(A,B) 計算向量A和B的 pearson 相關系數,B省略時用 to(A.len())
@r 計算 r2,即 pearson(norm@0(A),norm@0(B))
@a(…;k) 計算調整后的 r2,自由度為k
如何解釋 Pearson 相關系數?
| rr值范圍 | 相關性解釋 | ||
|---|---|---|---|
| 0.8< | r | < 1 | 強相關 |
| 0.5< | r | < 0.8 | 中等相關 |
| 0.3< | r | < 0.5 | 弱相關 |
| 0 < | r | < 0.3 | 極弱或無關 |
7.4 分析產品之間的銷量均值差異
產品 esProc 和其它產品之間的銷量均值是否存在較大差異?使用 t-test 分析即可得到答案:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(product,quantity) |
| 2 | =ttest_p(A1.(if(product==“esProc”:0;1)),A1.(quantity)) |
A2 ttest_p 函數為 SPL 中的 t-test 分析函數,輸入參數為兩組序列,第一組序列為 0、1 的二值序列,第二個序列為對應要分析的數值,該函數會自動根據 0、1 把第二個序列拆成兩組數進行比較。
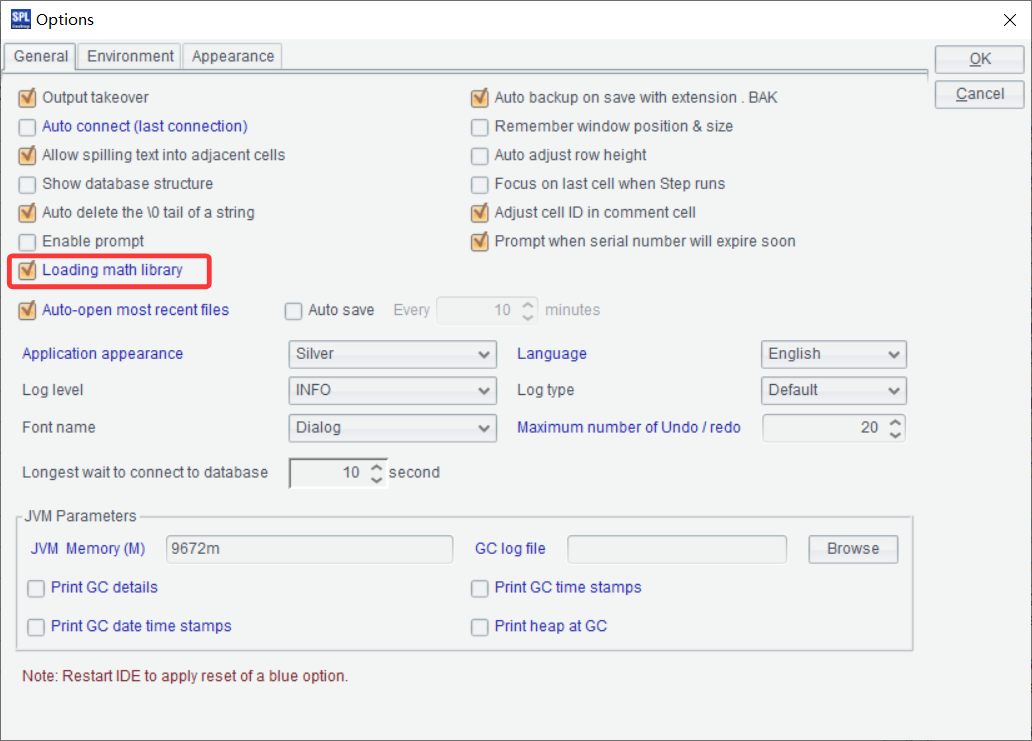
ttest_p 函數在外部庫中,需要先加載外部庫才能使用,加載步驟:
1、 點擊 Tool/Options
2、 勾選 Loading math library
知識點:ttest_p 函數
T 檢驗是一種統計假設檢驗方法,用于判斷兩組數據的均值是否存在顯著差異。它基于t 分布(Student’s t-distribution),適用于樣本量較小(通常 n<30)且總體方差未知的情況。
核心概念
- 目的:比較兩組數據的均值,判斷差異是否由隨機誤差引起,還是具有統計學意義。
- 適用條件:
- 數據近似服從正態分布(或樣本量足夠大,依賴中心極限定理)。
- 方差齊性(某些 T 檢驗要求組間方差相等)。
- 結果輸出:
- p 值:若 p<0.05(通常顯著性水平),則認為差異顯著。
函數語法:
ttest_p(X, Y) T 檢驗求p值。
應用舉例
- 比較 A/B 測試中兩組用戶的點擊率是否有顯著差異。
- 比較同一組樣本在不同條件下的差異(如服藥前后的血壓變化)。
- 檢驗減肥訓練前后學員體重的變化是否顯著。
如果想分析所有產品之間的銷量均值差異,可以使用 ANOVA 分析,在 SPL 中為 fisher_p 函數:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(product,quantity) |
| 2 | =fisher_p(A1.(product),A1.(quantity)) |
A2 fisher_p 函數適合多組數據之間的均值差異比較,不需要將數據拆成多組,而是直接把分組字段的值序列和數值序列傳給 fisher_p 函數即可,函數會自動根據分組字段將數值拆成多組進行比較
知識點:fisher_p 函數
fisher_p 函數采用 ANOVA(Analysis of Variance,方差分析),是一種用于比較三個或更多組均值是否存在顯著差異的統計方法。它的核心思想是通過分析數據中的方差(變異性)來判斷組間差異是否顯著大于組內差異。
核心概念
(1) 為什么要用 ANOVA?
- T 檢驗的局限性:T 檢驗只能比較兩組均值,而多組比較時,若逐一兩兩比較會增加Type I 錯誤(假陽性)的概率。
- ANOVA 的優勢:一次性檢驗多組均值差異,控制整體錯誤率。
(2) 基本假設
- 正態性:各組數據近似服從正態分布(或樣本量足夠大)。
- 方差齊性(Homogeneity of Variance):各組的方差應相近(可通過 Levene 檢驗判斷)。
- 獨立性:觀測值之間相互獨立(如不同組的樣本無關聯)。
(3) 假設檢驗
- 原假設(H?):所有組的均值相等(μ? = μ? = … = μ?)。
- 備擇假設(H?):至少有兩組的均值不等。
函數語法
fisher_p(X, Y) F 檢驗求p值。
ANOVA vs T 檢驗
| 對比項 | ANOVA | T 檢驗 |
|---|---|---|
| 比較組數 | ≥3 組 | 2 組 |
| 適用場景 | 多組均值差異 | 兩組均值差異 |
| 后續分析 | 需要事后檢驗 | 直接解釋結果 |
| 統計量 | F 值 | t 值 |
4. 結果解釋
- p 值:
- 若 p<0.05,拒絕 H?,認為至少有兩組均值不同。
- 若 ANOVA 顯著,需通過事后檢驗確定具體差異組。
7.5 客戶交易數據的 RFM 分析
通過評估客戶購買行為,對交易數據進行 RFM(最近一次消費、消費頻率、消費金額)分析。通過定義一個自定義函數,它接收三個輸入參數:交易數據、參考日期。其中最近消費時間(R)計算為客戶最后一次購買距今的天數,數值越小越好;消費頻率(F)是購買總次數,數值越高表示互動越頻繁;消費金額(M)指總支出金額,花費越多代表客戶價值越高。為統一量綱,每個分量會被排序并轉換為 0 到 5 分的標準分——最近消費時間按降序排列(因近期交易更理想),而消費頻率和消費金額按升序排列(因更多消費次數和更高金額更優)。
| A | B | |
|---|---|---|
| 1 | =file(“sales.csv”).import@ct(customer,orderDate,quantity,price,discount) | |
| 2 | func rfm_score(data,current_date) | |
| 3 | =data.groups(customer; interval(max(orderDate),current_date):recency, count(1):frequency, sum(quantity*price*discount):monetary) | |
| 4 | =B3.len() | |
| 5 | =B3.derive(:r_score,: f_score,:m_score) | |
| 6 | =B5.sort(recency:-1).run(r_score=rank(recency)/B4*5) | |
| 7 | =B5.sort(frequency).run(f_score=rank(frequency)/B4*5) | |
| 8 | =B5.sort(monetary).run(m_score=rank(monetary)/B4*5) | |
| 9 | return B5 | |
| 10 | =rfm_score(A1,now()) | |
A1 從文件 sales.csv 讀數
A2 定義了一個函數,函數名為 rfm_score,參數為 data, current_date
B3 將輸入參數 data 按客戶分組,統計最近一次下單距離參考日期的時長,下單次數、總下單金額
B4 統計 B3 的總記錄數
B5 添加三個字段 r_score,f_score,m_score
B6-B8 分別計算 r_score,f_score,m_score 三個字段的值,表達式 rank(recency)/B4*5 的含義是:按 recency 計算排名,然后除以總記錄數,獲得位次占比,最后乘以 5,返回值即為 0-5 分。其余兩個字段類似,只是排序規則相反。
B9 函數返回結果
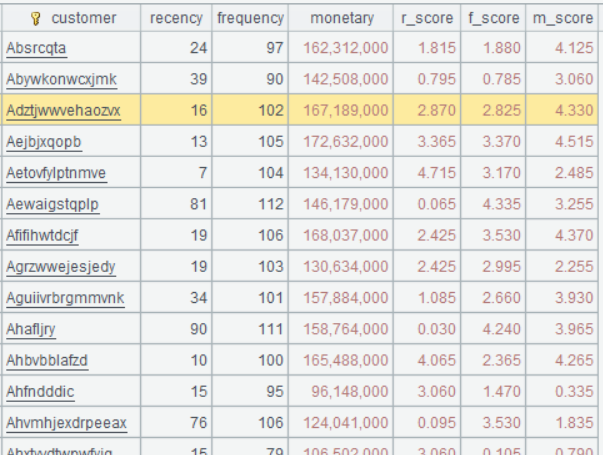
A10 調用自定義函數 rfm_score,傳入參數 A1,now()。
A10 的運行結果:
知識點:什么是代碼塊?
如下圖所示:
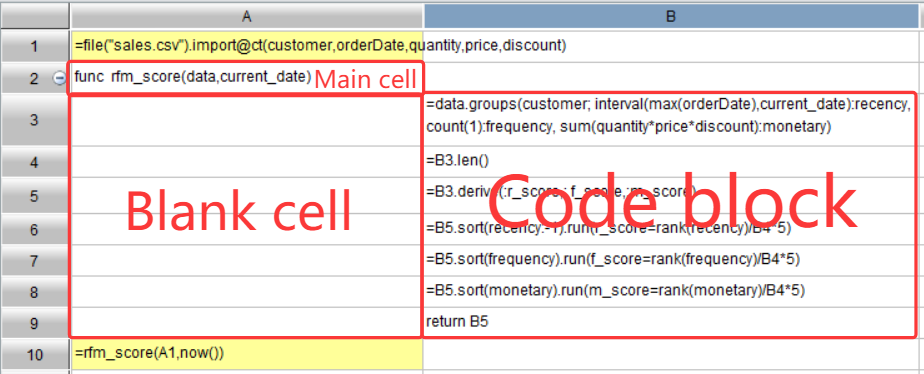
A2 為非空單元格,其下單元格片區 A3:A9 均為空白格,A10 非空,那么 B3:B9 單元格稱為以 A2 為主格的代碼塊。
代碼塊的核心特性
- 縮進敏感:
- 相同縮進層級屬于同一代碼塊
- 通常使用一個空白單元格作為縮進單位
- 作用域規則:
- 代碼塊內定義的變量只在塊內有效
- 可以訪問外部作用域的變量
- 流程控制:
- 分支和循環語句通過縮進形成代碼塊
主要應用場景
1. 函數定義
| A | B | C | |
|---|---|---|---|
| 1 | =func factorial(n) | ||
| 2 | if n==1 | ||
| 3 | return 1 | ||
| 4 | else | ||
| 5 | return n*factorial(n-1) | ||
2. 條件判斷
| A | B | |
|---|---|---|
| 1 | =x=10 | |
| 2 | if x>5 | |
| 3 | =“>5” | |
| 4 | else | |
| 5 | =“<=5” | |
3. 循環結構
| A | B | |
|---|---|---|
| 1 | =i=1 | |
| 2 | for i<=5 | |
| 3 | >output=output+" "+string(i) | |
| 4 | >i=i+1 | |
4. 異常處理
| A | B | |
|---|---|---|
| 1 | try | |
| 2 | =1/0 | |
| 3 | if A1!=null | |
| 4 | =“error” | |
| 5 | else | |
| 6 | =“correct” | |
多級代碼塊示例
| A | B | C | D | |
|---|---|---|---|---|
| 1 | =func process(data) | |||
| 2 | =result=[] | |||
| 3 | for data | |||
| 4 | if #B3%2==0 | |||
| 5 | =result.insert(0,B3) | |||
| 6 | return result | |||
代碼塊執行特點
- 獨立執行環境:每個代碼塊有獨立的變量作用域
- 返回值:最后一個表達式的值作為代碼塊的返回值
- 網格坐標引用:可以通過單元格坐標 (如 A1) 跨代碼塊引用值
與 Excel 公式的區別
- 結構化編程:支持真正的代碼塊和流程控制
- 變量作用域:比 Excel 的單元格引用更靈活
- 函數特性:支持遞歸、高階函數等高級特性
集算器 SPL 的這種基于網格和縮進的代碼塊設計,既保留了類似 Excel 的直觀性,又提供了完整的編程能力,非常適合處理復雜的數據計算任務。
知識點:自定義函數
基本語法:
| A | B | |
|---|---|---|
| 1 | =func funcName(arg1,arg2,……) | |
| 2 | Indented Function Block |
完整函數定義示例
1. 基礎函數
| A | B | |
|---|---|---|
| 1 | =func add(a,b) | |
| 2 | =a+b | |
| 3 | return B2 | |
| 4 | =add(3,5) | |
A1 函數定義開始
B2 函數體(縮進一格)
B3 返回值(可省略,默認返回最后表達式值)
A4 調用函數,返回 8
2. 帶默認參數的函數
| A | B | |
|---|---|---|
| 1 | =func greet(name=“Guest”,greeting=“Hello”) | |
| 2 | =greeting+“,”+name+“!” | |
| 3 | return B2 | |
| 4 | =greet() | |
| 5 | =greet(“John”) | |
| 6 | =greet(“Mary”,“Hi”) | |
A4 返回 "Hello, Guest!"
A5 返回 "Hello, John!"
A6 返回 "Hi, Mary!"
函數代碼塊特性
- 縮進規則:
- 函數聲明后所有縮進相同空格數的單元格都屬于函數體
- 通常使用1 個空格作為標準縮進量
- 作用域控制:
- 函數內部變量與外部隔離
- 可以訪問外部全局變量(需謹慎使用)
- 多語句執行:
- 函數體可以包含多個按順序執行的語句
7.6 根據 RFM 分析結果,將客戶分成五類
根據上例中 RFM 的分析結果,將客戶分成五類,采用兩種分類方法,一種是直接按 r_score,f_score,m_score 三種分值分類,另一種是按加權過的分值分類
方法一:
| A | |
|---|---|
| … | // 接上例 |
| 11 | =kmeans(A10.([r_score,f_score,m_score]),5) |
| 12 | =kmeans(A11,A10.([r_score,f_score,m_score])) |
A11 將客戶的 r_score,f_score,m_score 分值按 kmeans 聚類方法,把客戶分成五類。kmeans 函數是 SPL 中的采用經典的無監督學習聚類算法函數,后面會詳細介紹。
A12 根據 A11 的聚類結果,返回每個客戶歸屬的分類號,分類號相同的客戶,意為同一類
A12 的運行結果:
方法二:給三種分值加權重,其中銷售額最重要,權重為 3,購買次數次之,權重為 2,最近購買日期權重為 1,重新分類:
| A | |
|---|---|
| … | // 接上例 |
| 11 | =kmeans(A10.([r_score,f_score*2,m_score*3]),5) |
| 12 | =kmeans(A11,A10.([r_score,f_score*2,m_score*3])) |
A12 的運行結果為:
知識點:kmeans 函數
kmeans 算法概述
K-means 是一種經典的無監督學習聚類算法,它將數據集劃分為 K 個簇 (cluster),使得同一簇內的數據點相似度高,而不同簇的數據點相似度低。
kmeans 函數語法
kmeans(X, k) 用 k-means 聚類算法將矩陣 X 分成 k 個簇,返回擬合模型 B
kmeans(B, A) 用 k-means 聚類算法,根據擬合模型 B,分析數據A,返回 A 歸屬的簇序號
kmeans 算法步驟
- 初始化:隨機選擇 K 個點作為初始質心 (中心點)
- 分配步驟:將每個數據點分配到最近的質心所在的簇
- 更新步驟:重新計算每個簇的質心 (取簇中所有點的均值)
- 重復:重復步驟 2-3 直到質心不再顯著變化或達到最大迭代次數
kmeans 的應用場景
1. 客戶細分
- 根據購買行為、人口統計特征對客戶進行分組
- 用于精準營銷和個性化推薦
2. 圖像壓縮
- 將圖像顏色減少到 K 種代表性顏色
- 減少存儲空間同時保持視覺質量
3. 文檔分類
- 對文本文檔進行聚類
- 發現文檔集合中的主題群組
4. 異常檢測
- 識別遠離任何簇中心的異常點
- 用于欺詐檢測、網絡入侵檢測等
5. 市場細分
- 根據地理位置、消費習慣等對市場進行劃分
- 幫助制定區域化營銷策略
kmeans 的優缺點
優點:
- 簡單、易于理解和實現
- 計算效率高,適用于大規模數據集
- 對于球形簇結構的數據效果良好
缺點:
- 需要預先指定 K 值
- 對初始質心選擇敏感
- 對噪聲和異常值敏感
- 只能發現球形簇,難以處理復雜形狀的簇



)




)










