深度學習——詳細教學：神經元、神經網絡、感知機、激活函數、損失函數、優化算法（梯度下降）

神經網絡實戰：

深度學習——神經網絡簡單實踐（在乳腺癌數據集上的小型二分類示例）-CSDN博客https://blog.csdn.net/2302_78022640/article/details/150779819?spm=1001.2014.3001.5502

深度學習——神經網絡（PyTorch 實現 MNIST 手寫數字識別案例）-CSDN博客https://blog.csdn.net/2302_78022640/article/details/150781035

深度學習：人工智能的核心驅動力

一、什么是深度學習

深度學習（Deep Learning）是機器學習的一個重要分支

其核心是通過構建多層神經網絡（深度神經網絡）?模擬人類大腦的信息處理方式，從數據中自動學習特征和規律，最終實現對復雜任務的預測、分類或生成。

與傳統的機器學習相比，深度學習能夠自動從數據中提取特征，減少人工設計特征的工作量，并在語音識別、圖像處理、自然語言處理等領域取得了突破性成果。

通俗來說，深度學習的本質是用多層非線性變換將原始數據映射到更高層次的抽象特征空間，從而讓計算機更好地理解復雜問題。

二、深度學習的核心要素

1. 神經網絡（Neural Network）

大腦中的神經元：

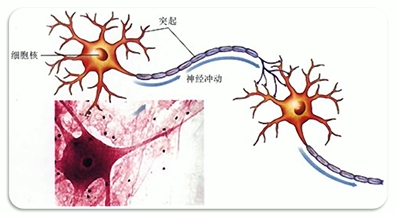
計算機中的神經元：

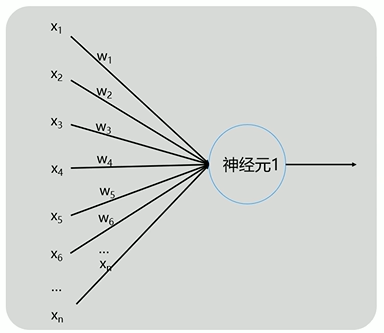
x1~xn這些外部信息，通過w1~wn這些突觸，傳入到神經元，神經元再傳給其他神經元或輸出。

怎樣得到這樣的神經元（推導）：

邏輯回歸（Logistic Regression）?是神經網絡的理論基礎之一。

邏輯回歸模型的形式和 單層感知機（即由一個或多個神經元構成的最簡單神經網絡（沒有隱藏層））很相似：

輸入 → 權重加權求和 → 激活函數 → 輸出概率。

單層感知機與邏輯回歸的主要不同在于激活函數

所以以邏輯回歸為例，為了得到劃分線

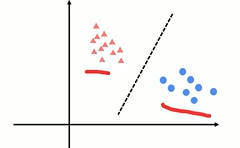
假設y=kx+b:

最終得到的結果可變換為矩陣形式即：

得到的神經元即可表達為：

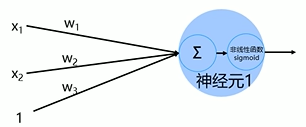
?非線性函數sigmoid曲線（激活函數）：

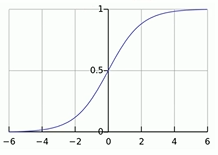
神經元（Neuron）是 神經網絡的基本計算單元

神經元的作用：

輸入 → 權重加和 → 激活函數 → 輸出

訓練神經網絡所要得到的目標就是：最優參數權重Wi和偏置b（b在此神經元內即是w3）

而目前得到的權重Wi和偏置b 并非最優

訓練過程：

我們輸入大量訓練數據

神經元根據當前的權重和偏置計算輸出

與真實標簽比較（用損失函數）

通過反向傳播調整權重 wi 和偏置 b，讓輸出越來越接近真實標簽。

整個神經網絡：由很多神經元組成，層層堆疊，訓練后形成能解決任務的模型。

每個節點代表一種特定的輸出函數，稱為激活函數（activation function）。

兩個節點間的連接都代表一個對于通過該連接信號的加權值，稱之為權重。

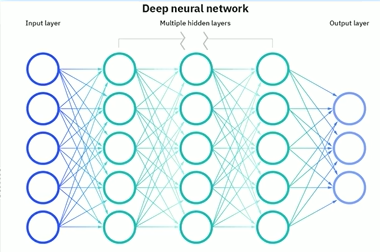
（中間綠色為神經元，兩側為輸入輸出）

1、設計一個神經網絡時，輸入層與輸出層的節點數往往是固定的，中間層則可以自由指定；

2、神經網絡結構圖中的拓撲與箭頭代表著預測過程時數據的流向，跟訓練時的數據流有一定的區別；

3、結構圖里的關鍵不是圓圈（代表“神經元”），而是連接線（代表“神經元”之間的連接）。每個連接線對應一個不同的權重（其值稱為權值），這是需要訓練得到的。

節點該如何確定？

輸入層的節點數：與特征的維度匹配

輸出層的節點數：與目標的維度匹配。

中間層（隱藏層）的節點數：一般是根據經驗來設置。預設幾個可選值，通過切換這幾個值來看整個模型的預測效果，選擇效果最好的值作為最終選擇。

層次結構：輸入層 → 隱藏層 → 輸出層。（深度學習的“深”就來自于隱藏層的數量）

每個隱藏層 = 由多個神經元組成的一層

一個神經元是一個點，而一層通常包含幾十、幾百、甚至上千個神經元。
每一層的神經元 并行計算，然后把結果傳遞給下一層。

作用：

輸入層：接收原始數據（像素、特征）。（對于圖片，像素就是其特征）

隱藏層：由許多神經元組成，負責特征提取和非線性變換。

輸出層：最終給出預測結果。

2.感知機（Perceptron）

單層感知機：

（輸入層→ 輸出層，無隱藏層）

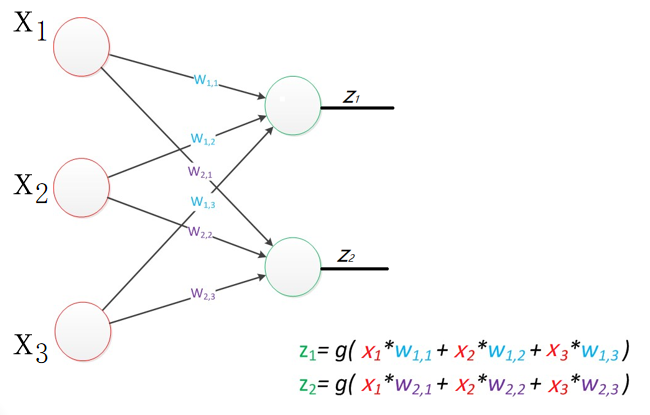
用矩陣乘法來表達：

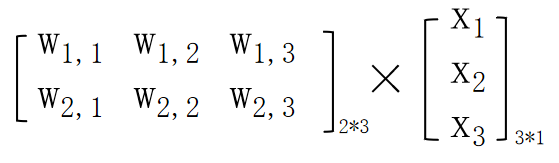
使用越階函數等激活函數，本質上是一種線性分類器，只能解決線性可分問題。

解釋：單層感知機的學習能力非常有限，對與像異或問題這樣的線性不可分情形，單層感知機就搞不定（線性不可分即輸入訓練數據，不存在一個線性超平面能夠將其進行線性分類）

單層感知機即使使用非線性激活函數（如 Sigmoid、ReLU 等），仍然無法解決非線性可分問題，核心原因在于其網絡結構的局限性，而非激活函數本身。“輸入特征的線性組合” 是對輸入的一次線性變換（即權重與輸入的內積），而激活函數只是對這個線性結果進行 “非線性映射”。

多層感知器：

多層感知機（MLP）是最經典、最基礎的神經網絡結構

增加了隱藏層。隱藏層是神經網絡可以做非線性分類的關鍵。

第一層的輸出是對輸入的 “非線性特征映射”（線性變換 + 激活函數）

第二層再對這些非線性特征進行線性組合 —— 最終的決策邊界可以是曲線、曲面等非線性形式。

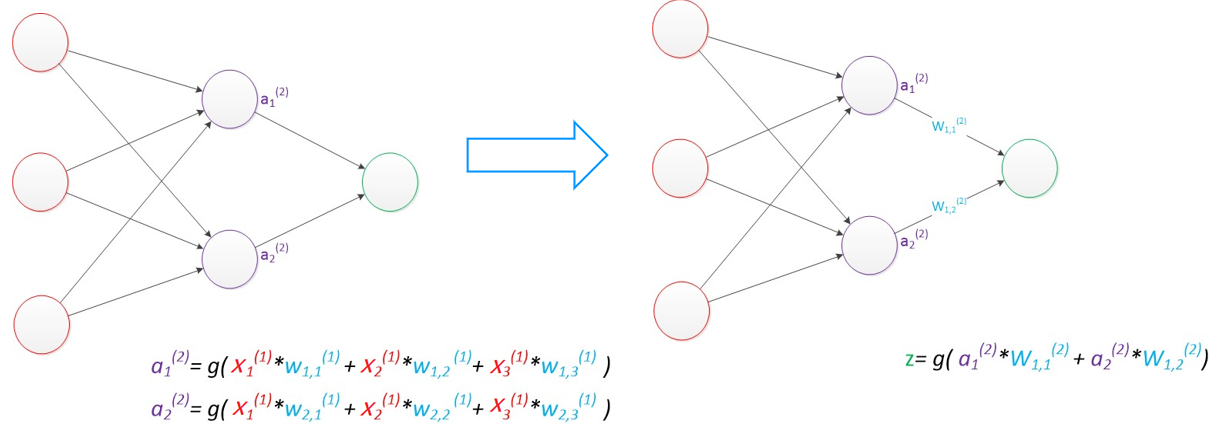
假設我們的預測目標是一個向量，那么與前面類似，只需要在“輸出層”再增加節點即可。

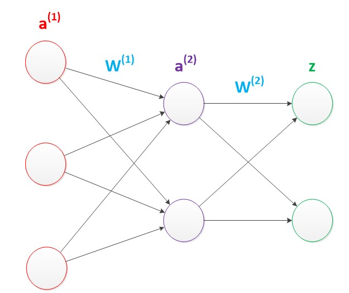
3. 激活函數（Activation Function）

激活函數是神經網絡的“非線性開關”

其核心作用是為網絡注入非線性能力，使模型能夠學習和表示復雜的非線性關系。

常見類型：

階躍函數：最簡單的激活函數，輸出只有 0 或 1。

激活函數	PyTorch 調用方式	輸出范圍	常見使用場景
Sigmoid	`nn.Sigmoid()` 或 `torch.sigmoid(x)`	(0, 1)	二分類輸出層
Tanh	`nn.Tanh()` 或 `torch.tanh(x)`	(-1, 1)	RNN、隱藏層
ReLU	`nn.ReLU()` 或 `torch.relu(x)`	[0, ∞)	CNN、MLP 隱藏層
Leaky ReLU	`nn.LeakyReLU(negative_slope=0.01)`	(-∞, ∞)	改進版 ReLU
ELU	`nn.ELU(alpha=1.0)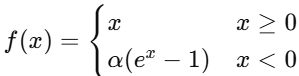`	(-α, ∞)	深層網絡
Swish	`torch.nn.SiLU()` 或 `torch.sigmoid(x) * x`	(-∞, ∞)	Google 深度 CNN
Softmax	`nn.Softmax(dim=1)` 或 `torch.softmax(x, dim=1)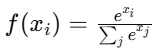`	(0,1)，和=1	多分類輸出層
Softplus	`nn.Softplus()`	(0, ∞)	特殊任務
Maxout	需自定義層	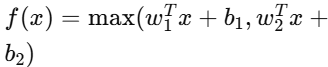(-∞, ∞)	NLP、圖像分類

為什么需要激活函數：

在神經元計算中：如果沒有激活函數，整個網絡就是線性函數的堆疊（多層線性還是線性），無法表示復雜關系。

激活函數的作用：

引入非線性：讓神經網絡能夠逼近任意復雜函數（通用逼近定理）。
增加表達能力：不同函數適合不同任務。
控制輸出范圍：比如 Sigmoid 把輸出壓縮到 (0,1)，適合概率建模。

4. 損失函數（Loss Function）

損失函數的作用：使得參數盡可能的與真實的模型接近。

1、衡量預測效果

如果損失值很小，說明預測結果和真實結果接近；
如果損失值很大，說明預測結果和真實結果差得遠。

2、指導參數更新

訓練神經網絡時，目標是 最小化損失函數
通過 梯度下降（Gradient Descent），我們利用損失函數對參數的梯度，更新神經元的權重和偏置。

3、防止過擬合 / 欠擬合

一些損失函數里會引入 正則化懲罰項（比如 L1/L2 正則化），幫助模型防止過擬合：? 通過在損失函數中加入 “正則項”（懲罰項），人為增加 “復雜模型” 的損失，迫使模型在 “擬合訓練數據” 和 “保持自身簡單” 之間做權衡

損失函數 = 預測誤差（如均方誤差、交叉熵） + 正則項（模型復雜度懲罰）

在訓練神經網絡中的損失函數：

輸入數據：外部信息xi（同時給所有參數賦上隨機值。我們使用這些隨機生成的參數值，來預測訓練數據中的樣本。)
前向傳播：計算預測值
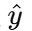
計算損失：用損失函數比較預測值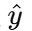? 和真實標簽 y
反向傳播：根據損失函數的梯度更新權重 W,b （BP神經網絡（Back-propagation，反向傳播））
迭代優化，直到損失函數收斂

常用的損失函數：

0-1損失函數

均方差損失（MSE）

平均絕對差損失

交叉熵損失（Cross Entropy）

合頁損失

損失函數	PyTorch 調用方式	數學公式	輸出范圍	常見使用場景
均方誤差 (MSELoss)	`nn.MSELoss()`		[0, ∞)	回歸任務
平均絕對誤差 (L1Loss/MAE)	- 不光滑，優化困難		y_i - \hat{y}_i	- 抗異常值
交叉熵 (CrossEntropyLoss)	`nn.CrossEntropyLoss()`		(0, ∞)	多分類任務
二元交叉熵 (BCELoss)	`nn.BCELoss()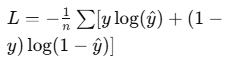`		(0, ∞)	二分類任務
帶 Logits 的 BCE (BCEWithLogitsLoss)	`nn.BCEWithLogitsLoss()`		(0, ∞)	二分類任務
KL 散度 (KLDivLoss)	- 不對稱	( D_{KL}(P		- 度量分布差異
Huber Loss (SmoothL1Loss)	[0, ∞)	(\text{Huber}(y,\hat{y})=\begin{cases} \frac{1}{2}(y-\hat{y})^2 &	y-\hat{y}	-\frac{1}{2}\delta) & \text{else} \end{cases})
負對數似然 (NLLLoss)	`nn.NLLLoss()`		(0, ∞)	多分類任務
余弦相似度損失 (CosineEmbeddingLoss)	`nn.CosineEmbeddingLoss()`		[0, 2]	序列/文本相似度
對比損失 (ContrastiveLoss)	需自定義實現		[0, ∞)	Siamese 網絡
Triplet Loss	`nn.TripletMarginLoss(margin=1.0)`		[0, ∞)	人臉識別、度量學習

5. 優化算法（Optimization）

深度學習常用的優化方法是 梯度下降（Gradient Descent）

梯度可以定義為一個函數的全部偏導數構成的向量，梯度向量的方向即為函數值增長最快的方向

不斷調整神經網絡的參數（權重 W?和偏置 b），使得損失函數的值盡可能小。

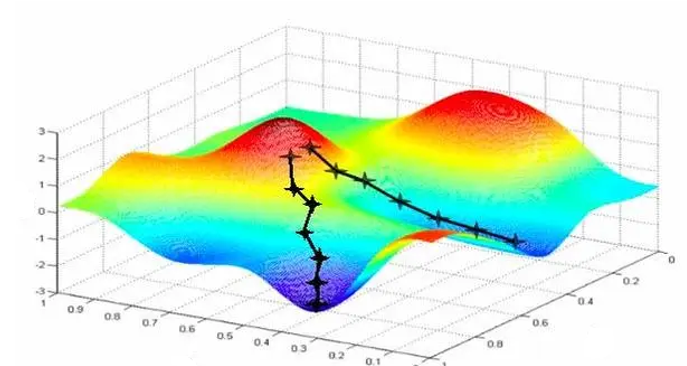
本質：

找到一個參數組合，使得損失函數 L(W,b) 達到最小值；
梯度下降就是通過不斷“往損失函數下降最快的方向走”，逐步接近最優解。

常見優化算法：

優化算法	PyTorch 調用方式	特點
批量梯度下降 (BGD)	手動實現，一般不用現成類	每次用全部數據更新
隨機梯度下降 (SGD)	`torch.optim.SGD(model.parameters(), lr=0.01)`	每次用單個樣本更新
小批量梯度下降 (Mini-Batch SGD)	`torch.optim.SGD(model.parameters(), lr=0.01, batch_size=32)`（通過 DataLoader 控制批量）	平衡了穩定性和效率
Adam	`torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9,0.999))`	結合 Momentum + RMSProp
Momentum	`torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)`	在 SGD 基礎上加動量項
NAG (Nesterov Accelerated Gradient)	`torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9, nesterov=True)`	預判未來位置再更新
Adagrad	`torch.optim.Adagrad(model.parameters(), lr=0.01)`	對每個參數自適應學習率
RMSProp	`torch.optim.RMSprop(model.parameters(), lr=0.001, alpha=0.9)`	引入指數加權平均
AdamW	`torch.optim.AdamW(model.parameters(), lr=0.001, weight_decay=0.01)`	改進 Adam 正則化