概率核心概念學習筆記：隨機事件與樣本空間、古典概率與條件概率、全概率公式與貝葉斯公式

一、隨機事件與樣本空間

1. 原理講解

2. 類型與關系

3. 案例計算

4. 應用場景

二、古典概率與條件概率

1. 古典概率 (Classical Probability)

2. 條件概率 (Conditional Probability)

三、全概率公式與貝葉斯公式

1. 全概率公式 (Law of Total Probability)

2. 貝葉斯公式 (Bayes‘ Theorem)

3. 兩者的邏輯關聯

一、隨機事件與樣本空間

1. 原理講解

概率論研究的是不確定性（隨機性）的規律。它的基礎是兩個核心概念：

樣本空間 (Sample Space)：記作 $S$ 或 $\Omega$ 。它是一個隨機試驗所有可能結果的集合。每個結果稱為一個樣本點。
隨機事件 (Random Event)：是樣本空間的子集。它表示我們“關心”的某些結果的集合。

2. 類型與關系

必然事件：一定會發生的事件，即樣本空間 $S$ 本身。（例如：擲骰子點數小于7）
不可能事件：一定不會發生的事件，即空集 $\varnothing$ 。（例如：擲骰子點數為0）
基本事件：只包含一個樣本點的事件。
復合事件：包含多個樣本點的事件。

關系：事件是樣本空間的子集，所以集合的運算（交 $\cap$ 、并 $\cup$ 、補 $\bar{A}$ ）完全適用于事件。

$A \cap B$ ：事件A?和?事件B?同時發生。
$A \cup B$ ：事件A?或?事件B?至少有一個發生。
$\bar{A}$ ：事件A?不發生（對立事件）。

3. 案例計算

試驗：擲一顆六面公平骰子。
- 樣本空間 $S$ ：{1, 2, 3, 4, 5, 6}
- 事件A（點數為偶數）：{2, 4, 6}
- 事件B（點數大于4）：{5, 6}
- 事件A與B的交集 $A \cap B$ ：{6} （即點數大于4且是偶數）
- 事件A與B的并集 $A \cup B$ ：{2, 4, 5, 6} （即點數為偶數或大于4）

4. 應用場景

構建任何概率問題的第一步都是明確樣本空間。它是我們計算概率的“分母”，是所有可能性的全集。無論是游戲抽卡、產品質量檢測還是社會調查，都需要先定義清楚所有可能的結果。

1. 游戲抽卡

一句話定義：?卡池里所有可被抽到的特定卡牌的集合。

簡單說明：假設一個卡池里有100張卡，包括80張普通卡（N）、15張稀有卡（R）和5張超級稀有卡（SSR）。那么樣本空間就是這100張各不相同卡的集合?{卡1, 卡2, 卡3, ..., 卡100}。你每次抽卡，結果必然是這個集合中的某一個元素。

2. 產品質量檢測

一句話定義：?被抽查的產品所有可能的質量狀態結果的集合。

簡單說明：最簡單的情況是產品只有“合格”與“不合格”兩種狀態。那么樣本空間就是?{合格, 不合格}。如果要更精細，樣本空間可以是所有可能缺陷類型的集合，例如?{合格, 外觀瑕疵, 功能故障, 包裝損壞, ...}。

3. 社會調查

一句話定義：?所有被調查者對于某個問題可能給出的所有答案的集合。

簡單說明：例如，調查“您對當前政策的滿意度如何？”，選項為“非常滿意”、“滿意”、“一般”、“不滿意”、“非常不滿意”。那么樣本空間就是這個選項集合?{非常滿意, 滿意, 一般, 不滿意, 非常不滿意}。每個被訪者的回答就是這個空間里的一個結果。

核心總結

場景樣本空間 (S) “一次試驗” “一個結果”
游戲抽卡 所有卡牌的集合抽一次卡抽到某一張特定的卡
質量檢測 所有質量狀態的集合檢測一個產品該產品被判定為某種狀態
社會調查 所有可能答案的集合詢問一個人這個人給出的某個特定答案

關鍵在于：?樣本空間必須窮盡所有可能（不能遺漏），且結果之間互斥（一個結果發生，其他結果就不發生）。

場景	樣本空間 (S)	“一次試驗”	“一個結果”
游戲抽卡	所有卡牌的集合	抽一次卡	抽到某一張特定的卡
質量檢測	所有質量狀態的集合	檢測一個產品	該產品被判定為某種狀態
社會調查	所有可能答案的集合	詢問一個人	這個人給出的某個特定答案

二、古典概率與條件概率

1. 古典概率 (Classical Probability)

原理：適用于樣本空間有限且每個基本事件發生的可能性完全相同的場景。概率計算轉化為“數數”問題。
公式：事件 $A$ 發生的概率
案例：
- 抽撲克牌，抽到A的概率： $P = \frac{4}{52} = \frac{1}{13}$
- 擲骰子得到偶數的概率： $P = \frac{3}{6} = \frac{1}{2}$
應用：賭博游戲（骰子、輪盤）、抽獎、簡單的隨機抽樣。前提是“公平”，即等可能性。

2. 條件概率 (Conditional Probability)

原理：在已知某個事件B已經發生的條件下，另一個事件A發生的概率。它引入了“信息”的概念，信息會改變概率。
公式： $P(A|B) = \frac{P(A \cap B)}{P(B)}$ （要求 $P(B) > 0$ ）
- $P(A|B)$ 讀作“在B發生的條件下A發生的概率”。
- 分子 $P(A \cap B)$ 是A和B同時發生的概率。
- 分母 $P(B)$ 是已知條件發生的概率。
案例：
- 擲一顆骰子。已知擲出的點數是奇數（事件B={1,3,5}），求該點數大于3（事件A={4,5,6}）的概率。
- $A \cap B = {5}$
- $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{1/6}{3/6} = \frac{1}{3}$
應用：幾乎所有現實場景！天氣預報（已知今天是晴天，明天下雨的概率）、推薦系統（已知用戶購買了A商品，其購買B商品的概率）、醫療診斷（已知檢測結果為陽性，真實患病的概率）。

三、全概率公式與貝葉斯公式

這兩個公式是條件概率的延伸，共同解決了“由因推果”和“由果溯因”的問題。

1. 全概率公式 (Law of Total Probability)

原理：如果事件 $B$ 的發生總是與一系列互斥（不相交）且完整（覆蓋所有可能性）的原因 $A_1, A_2, ..., A_n$ 之一有關，那么事件 $B$ 的總概率可以通過將所有不同途徑導致 $B$ 發生的概率加總得到。
公式：
$P(B) = P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + ... + P(B|A_n)P(A_n)$
案例（工廠質檢）：
- 某工廠有三條生產線（ $A_1$ , $A_2$ , $A_3$ ），產量占比分別為50%，30%，20%（即 $P(A_1)=0.5$ , $P(A_2)=0.3$ , $P(A_3)=0.2$ ）。
- 各生產線的次品率分別為1%，2%，3%（即 $P(B|A_1)=0.01$ , $P(B|A_2)=0.02$ , $P(B|A_3)=0.03$ ）。
- 問：隨機抽一個產品，它是次品( $B$ )的概率是多少？
- 計算：
  $P(B) = 0.01 \times 0.5 + 0.02 \times 0.3 + 0.03 \times 0.2 = 0.005 + 0.006 + 0.006 = 0.017$
應用：用于計算一個復雜事件的總概率，當該事件可以通過多種不同的、互斥的路徑發生時。

2. 貝葉斯公式 (Bayes‘ Theorem)

原理：它解決的問題是“逆概率”。當我們觀察到結果 $B$ 發生了，要反過來推斷這個結果是由某個原因 $A_i$ 造成的概率是多少。它用新證據（ $B$ ）來更新我們對該原因（ $A_i$ ）的信念（從先驗概率 $P(A_i)$ 更新為后驗概率 $P(A_i|B)$ ）。

公式：
$P(A_i|B) = \frac{P(B|A_i)P(A_i)}{P(B)} = \frac{P(B|A_i)P(A_i)}{\sum_{j=1}^{n} P(B|A_j)P(A_j)}$

分母 $P(B)$ 就是由全概率公式計算得出的。

案例（疾病檢測）：

某疾病患病率（先驗概率）
- P(患病)=0.01（即人群中1%的人患有該疾病）
- P(健康)=1?P(患病)=0.99（即人群中99%的人是健康的）
檢測準確率：P(陽性|患病) = 0.99 (靈敏度)，P(陽性|健康) = 0.05 (假陽性率)
問：如果一個人檢測結果是陽性，他真正患病的概率 P(患病|陽性)是多少？
計算：
1. 用全概率公式計算 P(陽性):P(陽性)=P(陽性∣患病)?P(患病)+P(陽性∣健康)?P(健康)，P(陽性)=0.99×0.01+0.05×0.99=0.0099+0.0495=0.0594
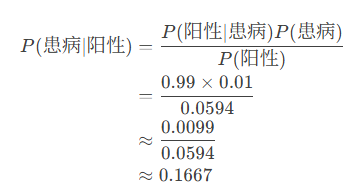
2. 用貝葉斯公式計算后驗概率:
結論：盡管檢測“很準確”，但一次陽性結果下真正患病的概率只有16.67%。這是因為患病率低，假陽性人數遠多于真陽性人數。這體現了貝葉斯“更新信念”的核心思想。
應用：
- 機器學習：垃圾郵件過濾（已知郵件內容，判斷是垃圾郵件的概率）。
- 醫療診斷：基于癥狀和檢測結果診斷疾病。
- 金融風控：評估用戶交易欺詐的概率。
- 人工智能：貝葉斯網絡是重要推理工具。

3. 兩者的邏輯關聯

全概率公式是正向思維：“原因” → “結果”。（由因推果）
貝葉斯公式是逆向思維：“結果” → “原因”。（由果溯因）
關鍵聯系：貝葉斯公式的分母 $\mathbf{P(B)}$ 必須通過全概率公式來計算。沒有全概率公式提供的“總概率”，貝葉斯公式就無法完成準確的逆向推理。

一句話總結：全概率公式是貝葉斯公式的基石，二者一正一反，共同構成了處理條件概率問題的強大工具包。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/94046.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/94046.shtml
英文地址，請注明出處：http://en.pswp.cn/web/94046.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！