從零手寫紅黑樹（C++實現詳解）

目錄

一、紅黑樹概述

二、紅黑樹節點設計

? (1)枚舉紅黑

（2）紅黑樹的節點設計

三、紅黑樹核心實現:Insert

1.首先將節點遍歷到對應位置創建對應節點并插入到二叉搜索樹對應的位置

2.本文重點的重點

（1）parent為黑時直接插入即可

（2）uncle存在且為紅

（3）uncle不存在

（4）uncle存在且為黑

四、紅黑樹檢查代碼

五、總代碼

1.RBTree.h

2.Test.c代碼

一、紅黑樹概述

學完AVL樹之后對我來說，紅黑樹可能更容易理解，還有水了這么多篇，該認真寫一篇了，哈哈哈哈。

紅黑樹顧名思義就是得有紅色和黑色的樹，紅黑樹利用紅色和黑色節點來創建二叉平衡搜索樹

紅黑樹的5條核心特點：

（1）每個節點是紅色或黑色

（2）根節點必須是黑色

（3）所有葉子節點（NIL/空節點）是黑色（NIL節點是紅黑樹中所有空指針的替代節點，表示樹的

葉子位置。）

（4）紅色節點的子節點必須是黑色（即不能有連續的黑色節點）

（5）從任意節點到其所有葉子節點的路徑上，黑色節點的數量相同

二、紅黑樹節點設計

? (1)枚舉紅黑

enum Colour
{RED,BLACK
};

（2）紅黑樹的節點設計

1.其中的三叉鏈是指_left _right _parent ,在我的理解中_left和_right是為了前進，而_parent是為了后退

2.kv是儲存的值，set中儲存的V是與K一樣的類型，map中儲存的是<const K ,V>

template<class K,class V> 
struct RBTreeNode
{//三叉鏈RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V> & kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};

三、紅黑樹核心實現:Insert

二叉樹的核心操作就是插入，插入分為三種情況:

（1）uncle存在且為紅

（2）uncle不存在

（3）uncle存在且為黑

1.首先將節點遍歷到對應位置創建對應節點并插入到二叉搜索樹對應的位置

	typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//意味著這里是一顆空樹，直接插入就行if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//這里是創建一個初始化_kv(kv)的新節點，并別把顏色初始化為紅色cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else if (parent->_kv.first > kv.first){parent->_left = cur;}cur->_parent = parent;

2.本文重點的重點

注：給出的圖畫是以 parent == grandfather->_left 條件下進行的,panret==grandfather->_right同理，最后有完整代碼可參考

（1）parent為黑時直接插入即可

！！！下面都是parent為紅的情況

（2）uncle存在且為紅

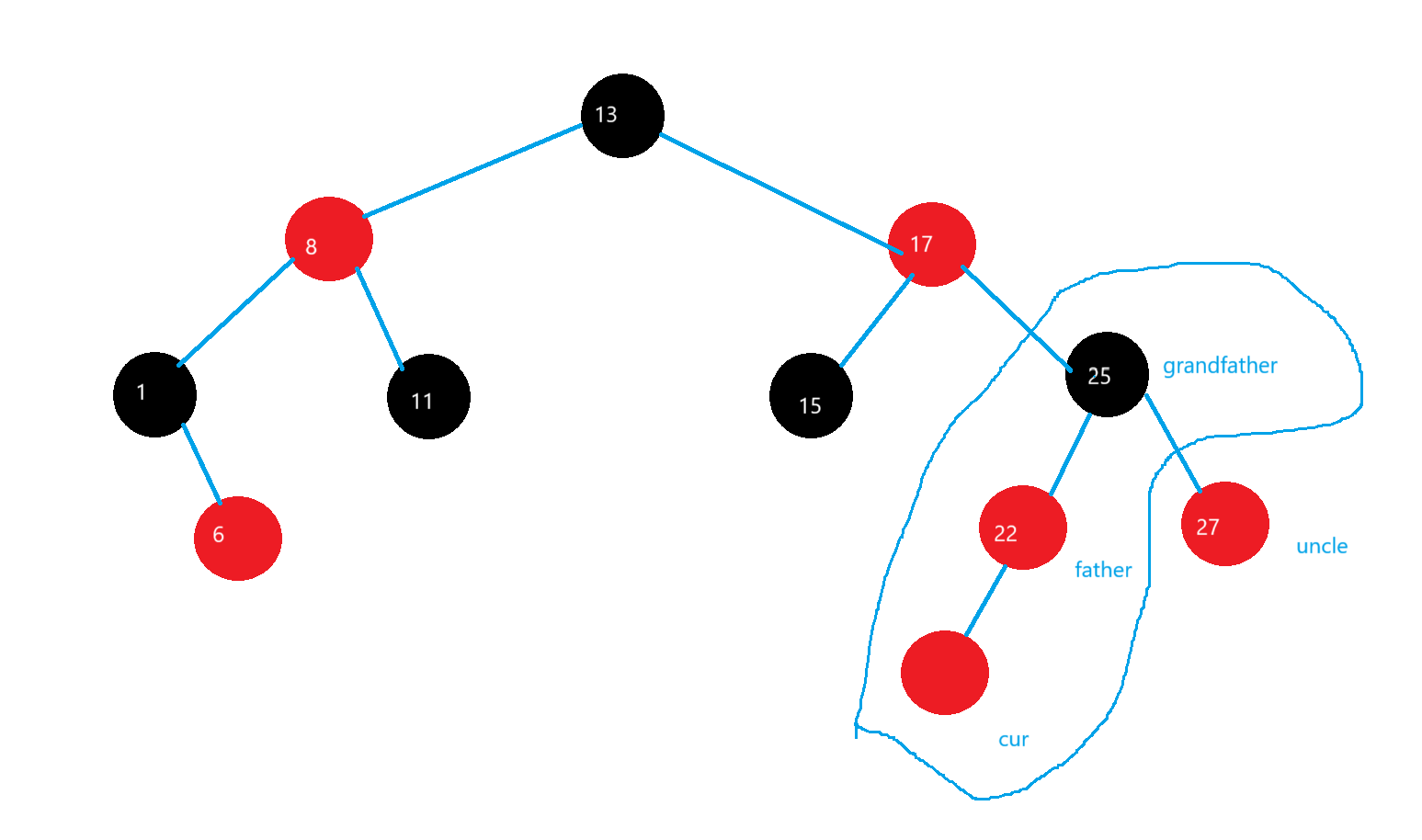
在parent和uncle為紅的情況我們，讓我們grandfatehr變成紅，讓parent和uncle變成黑

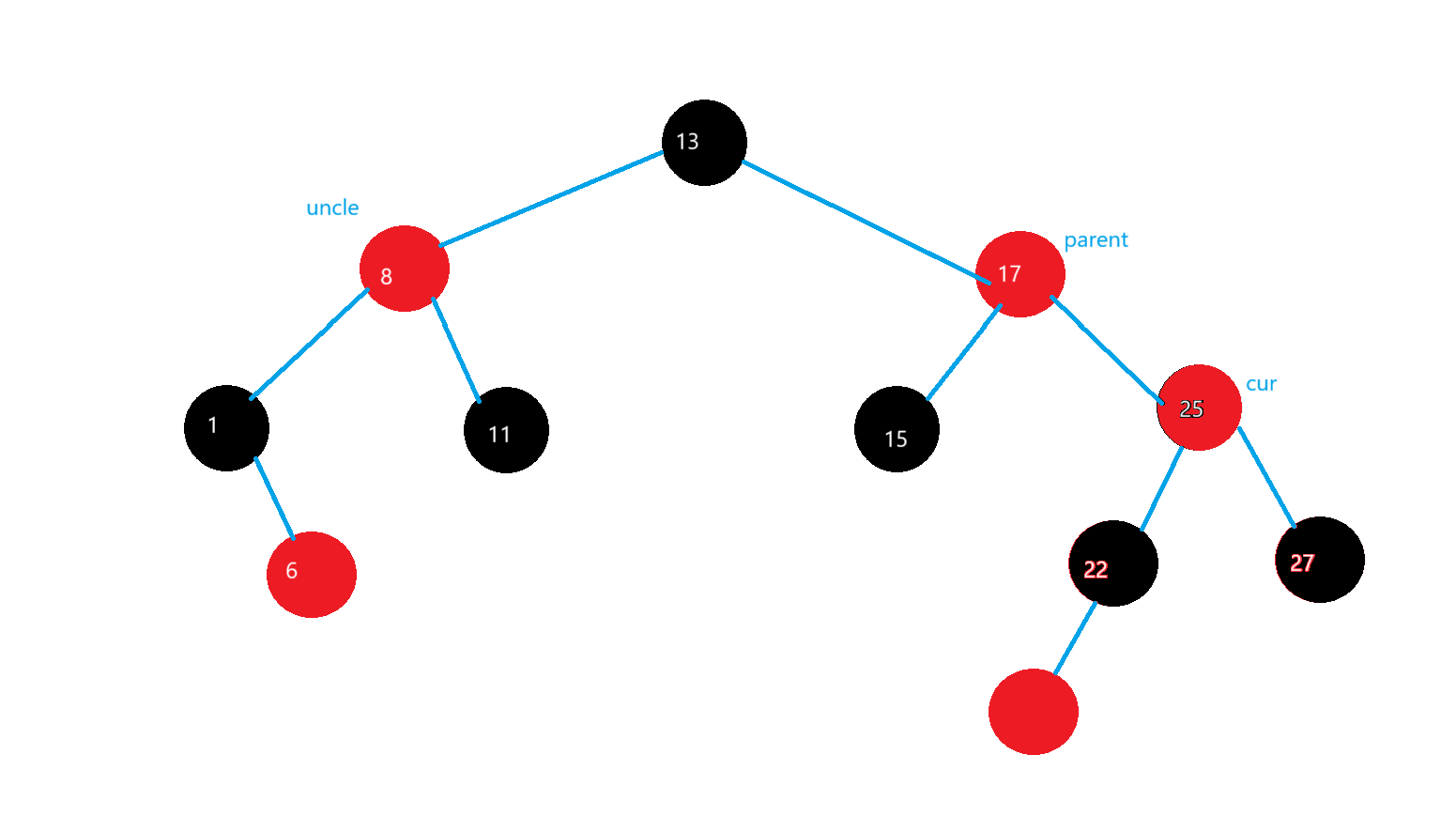
然后讓cur=grandfatehr ,parent=cur->_parent,grandfather=parent->_parent

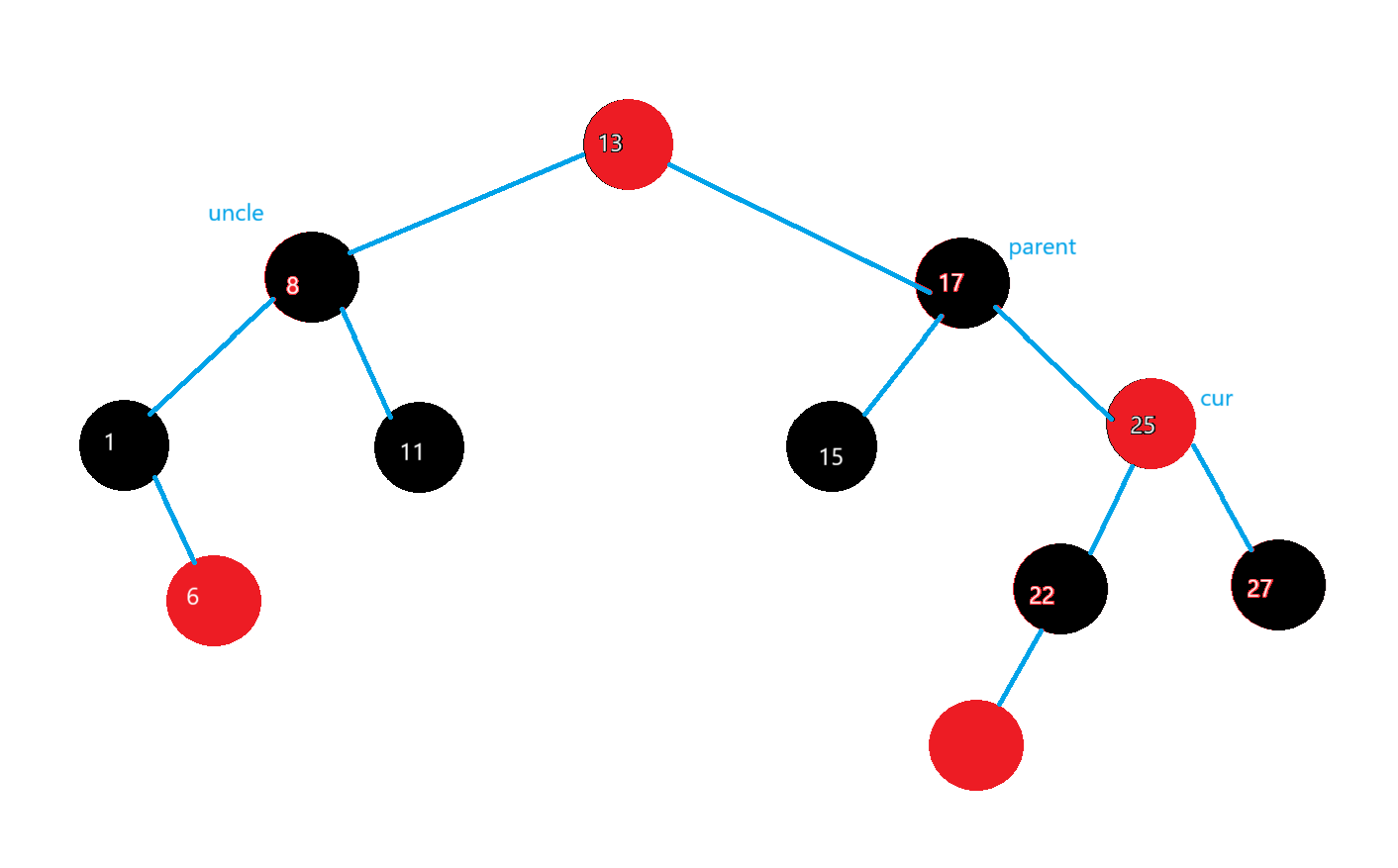
繼續向上處理：

（一）?.grandfather沒有父親，就是根，grandfatehr變黑即可

（二）.grandfather有父親，父親時黑色，就結束了

（三）.grandfather有父親，父親是紅色，和上面一樣處理

繼續像剛才一樣的操作

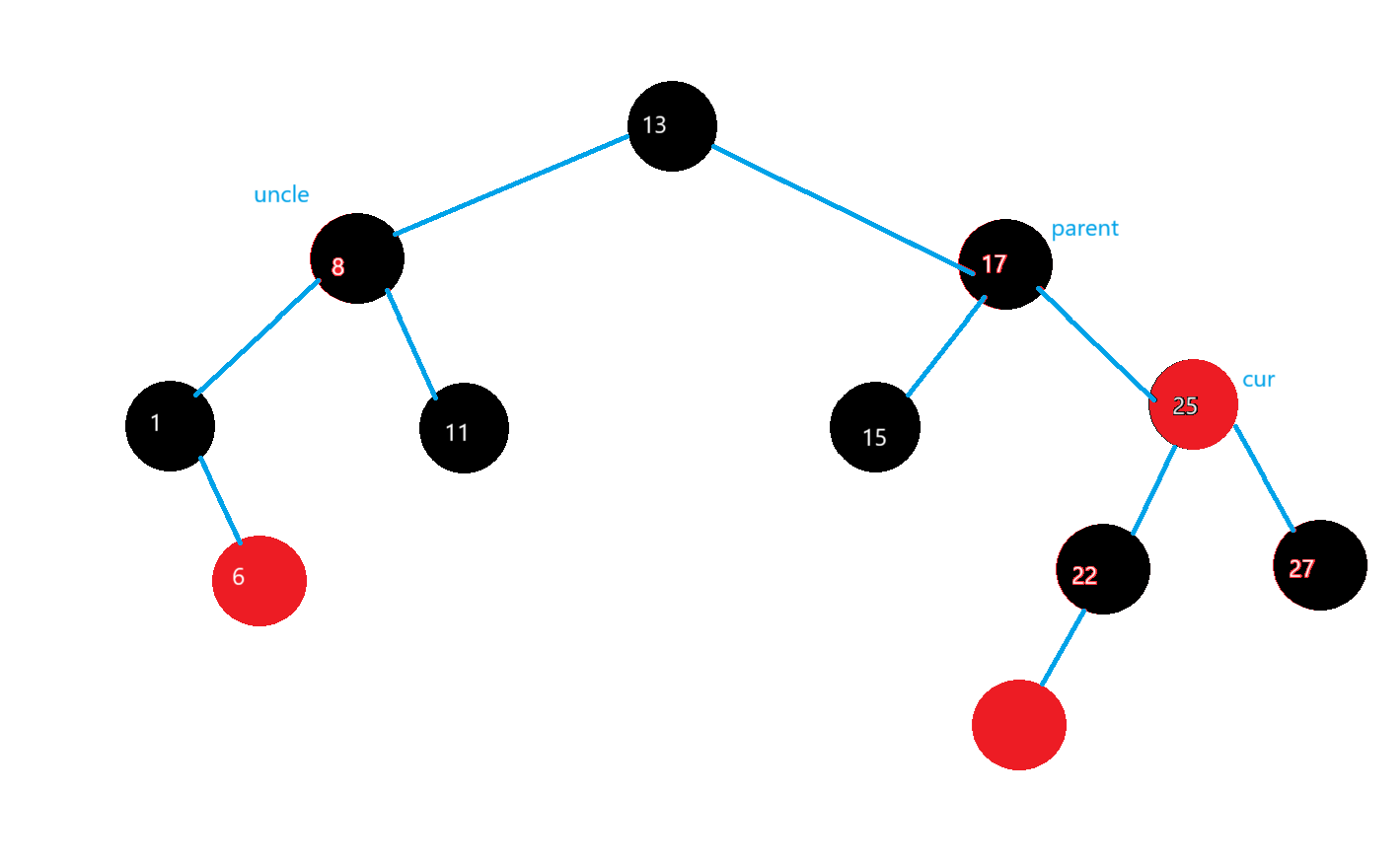
因為grandfatehr 是根節點，因為根節點只能是紅，最后讓根節點的顏色變成紅? ? ? ? ? ? ? ? ??

最后有完整代碼，現在給出對應部分代碼

Node* uncle = grandfather->_right;
//uncle存在且為紅
if (uncle && uncle->_col == RED)
{//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;//grandfather = parent->_parent; 
}
（3）uncle不存在

這里是grandfather->_left且parent是紅色節點的前提，這里有兩種情況

情況一：parent->_left=cur

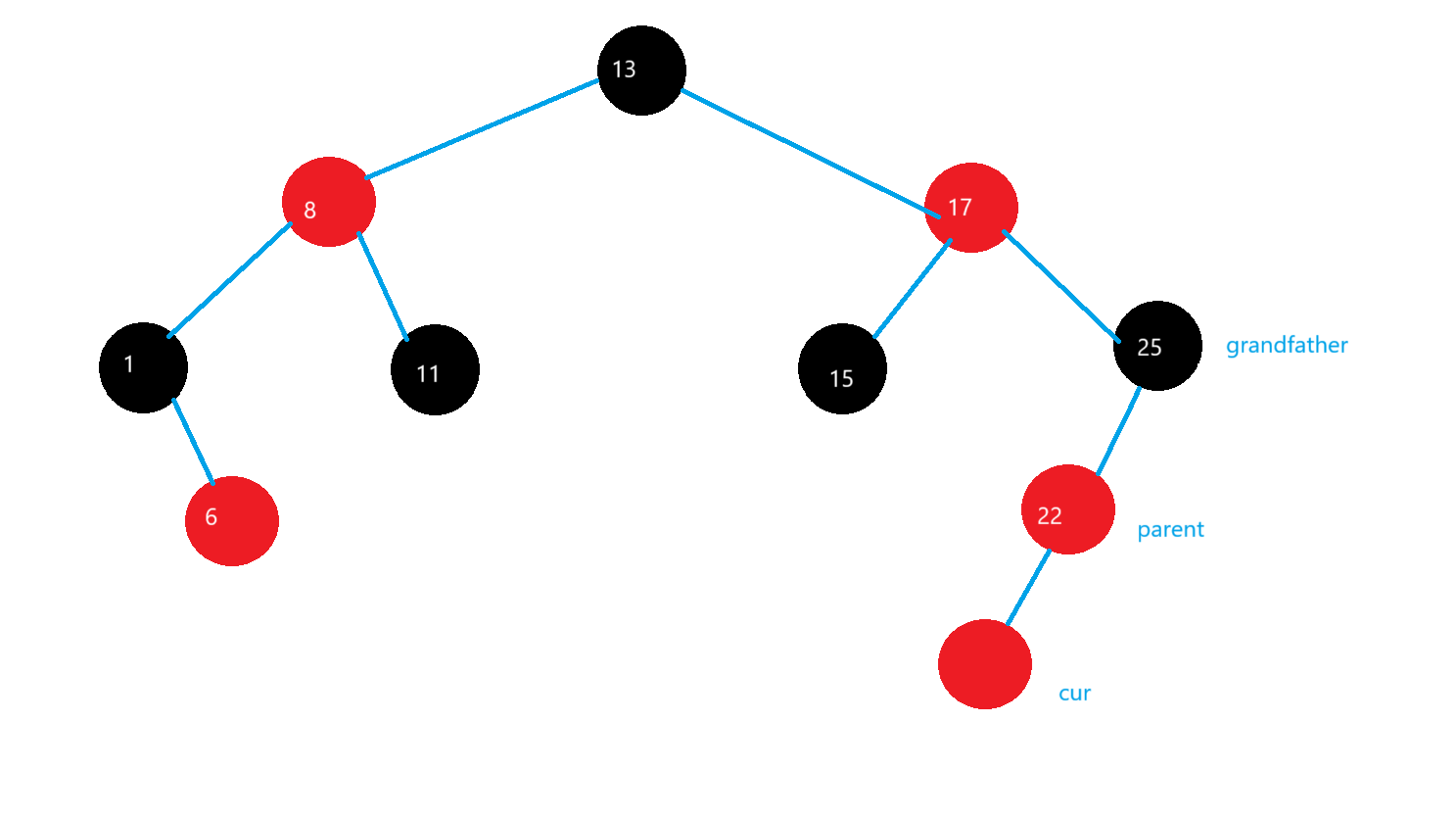
在grandfather節點進行右旋，讓grandfather的顏色變成紅色，讓parent的顏色變成黑色

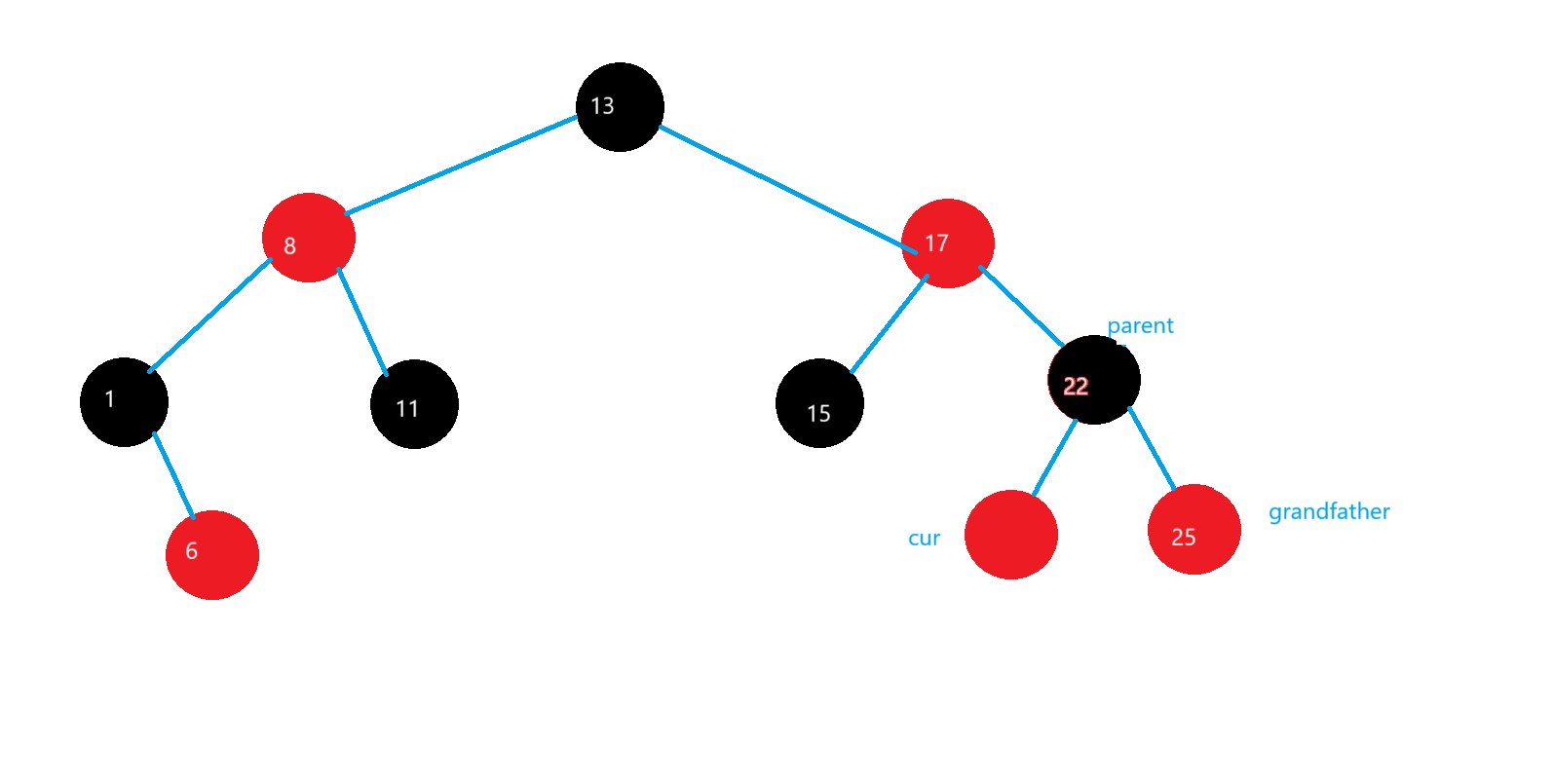
情況二:parent->_right=cur

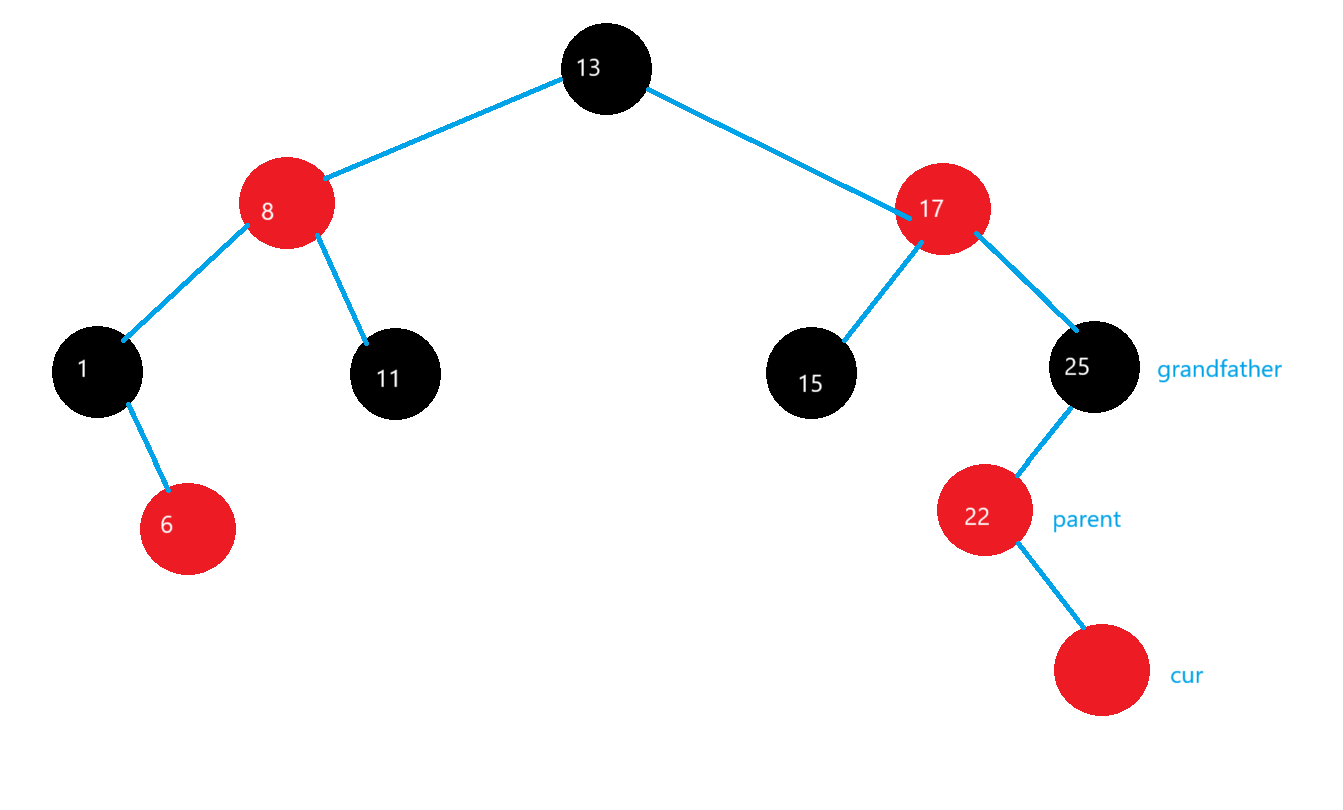
在parent節點進行左旋

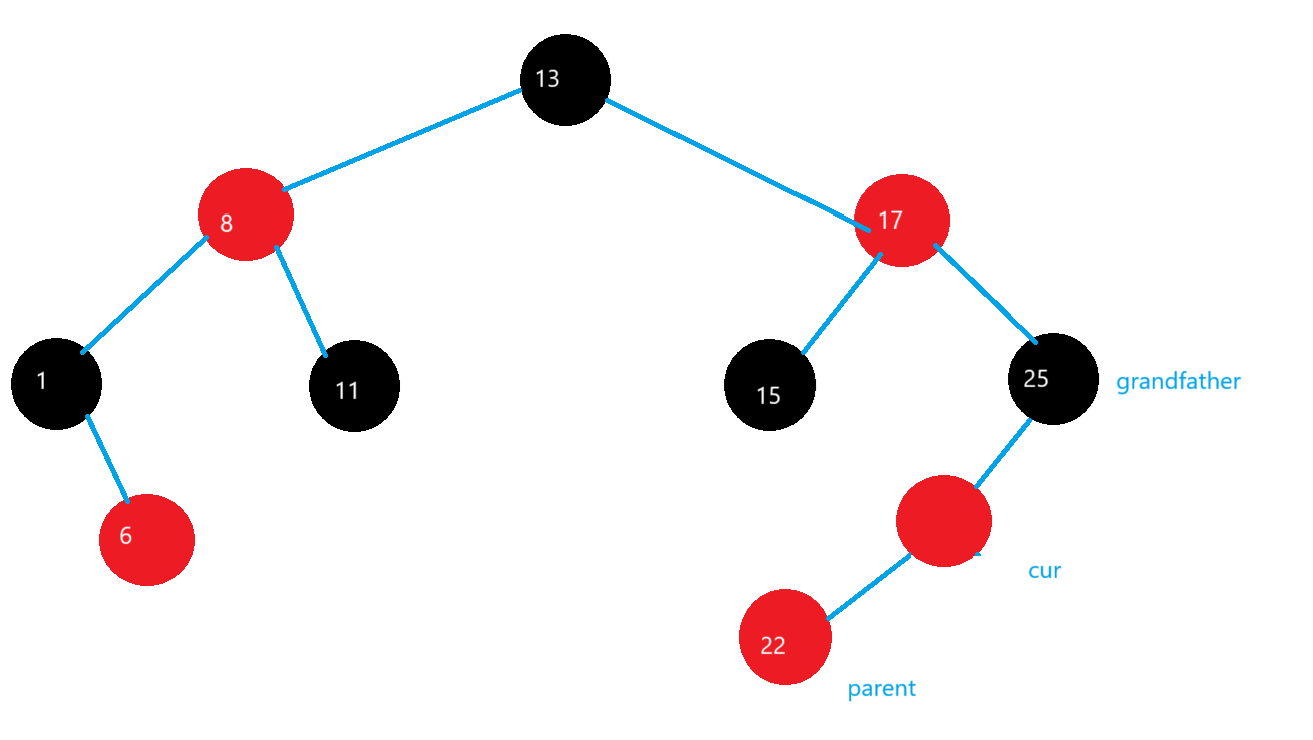
再在grandfather哪里進行右旋

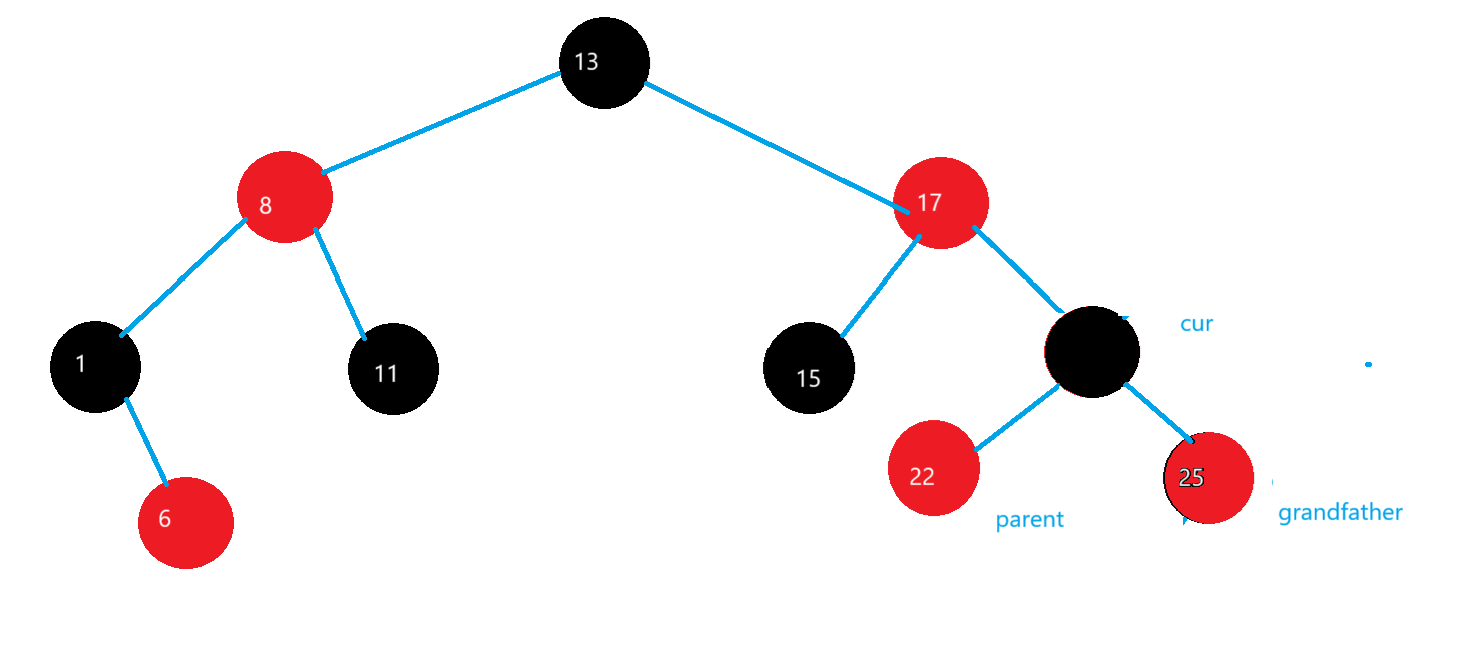
旋轉完之后，grandfather的顏色變紅，cur的顏色變黑

代碼：

現在給出對應部分代碼，左旋，右旋，左右旋，右左旋代碼也在最后的完整代碼中

else//uncle不存在或uncle存在且為黑
{//這是什么意思？這里我自己判斷了if (cur == parent->_left ){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED; }break;
}
（4）uncle存在且為黑

這里是grandfather->_right且parent是紅色節點的前提，與（3）的以grandfather->_left情況相反了

這種情況有點特殊，要操作一步才能得到

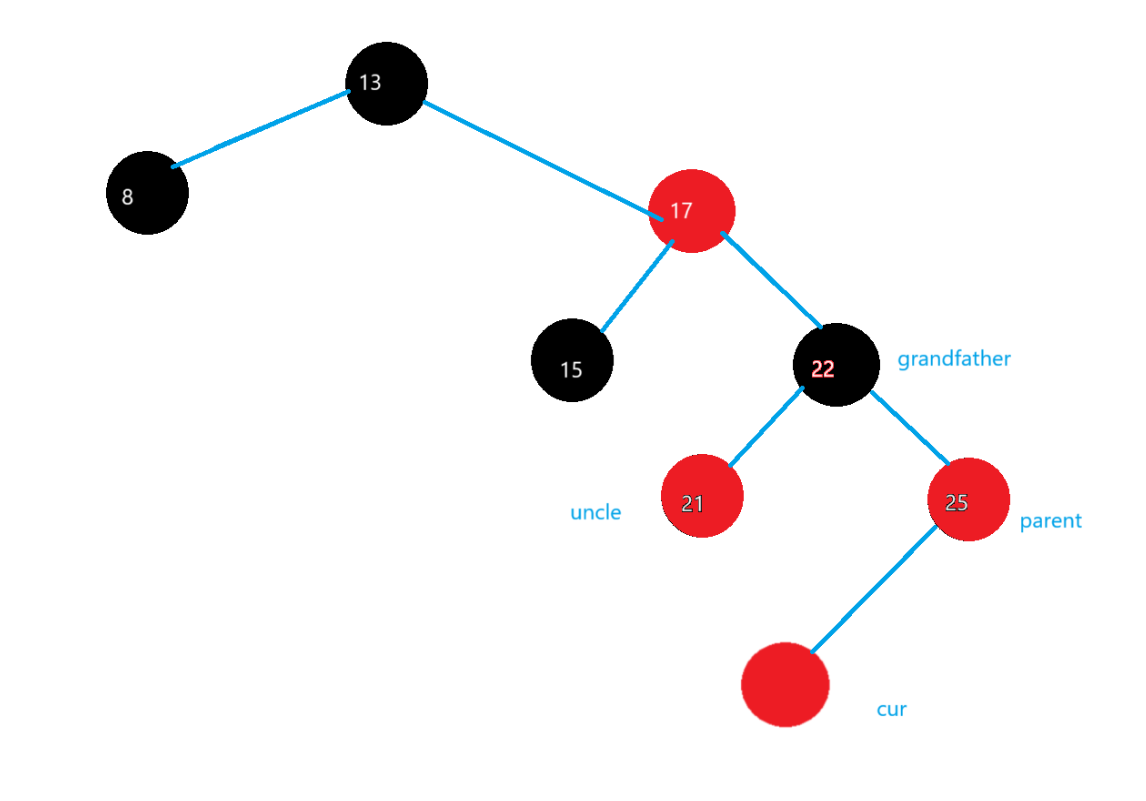
按照（2）變成，變成我們（4）所需要的狀態

情況一：parent->_right=cur

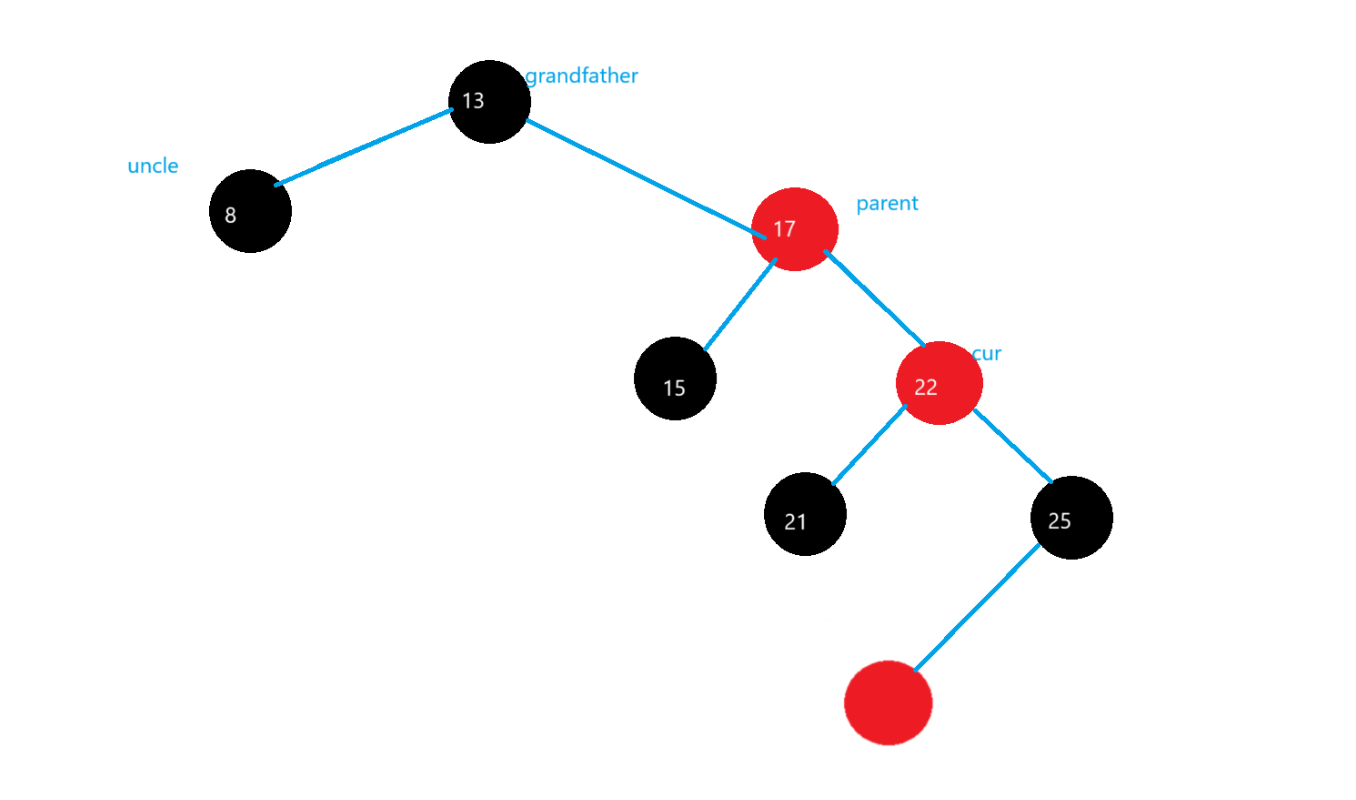
然后對grandfather進行左旋

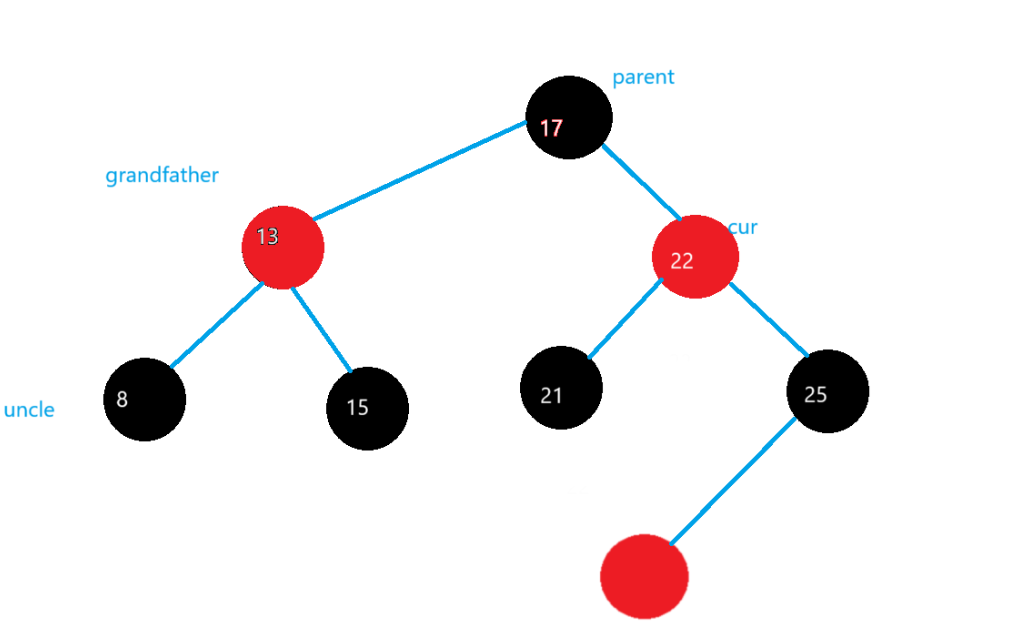
grandfather的顏色變紅，parent的顏色變黑

情況二：parent->_left=cur

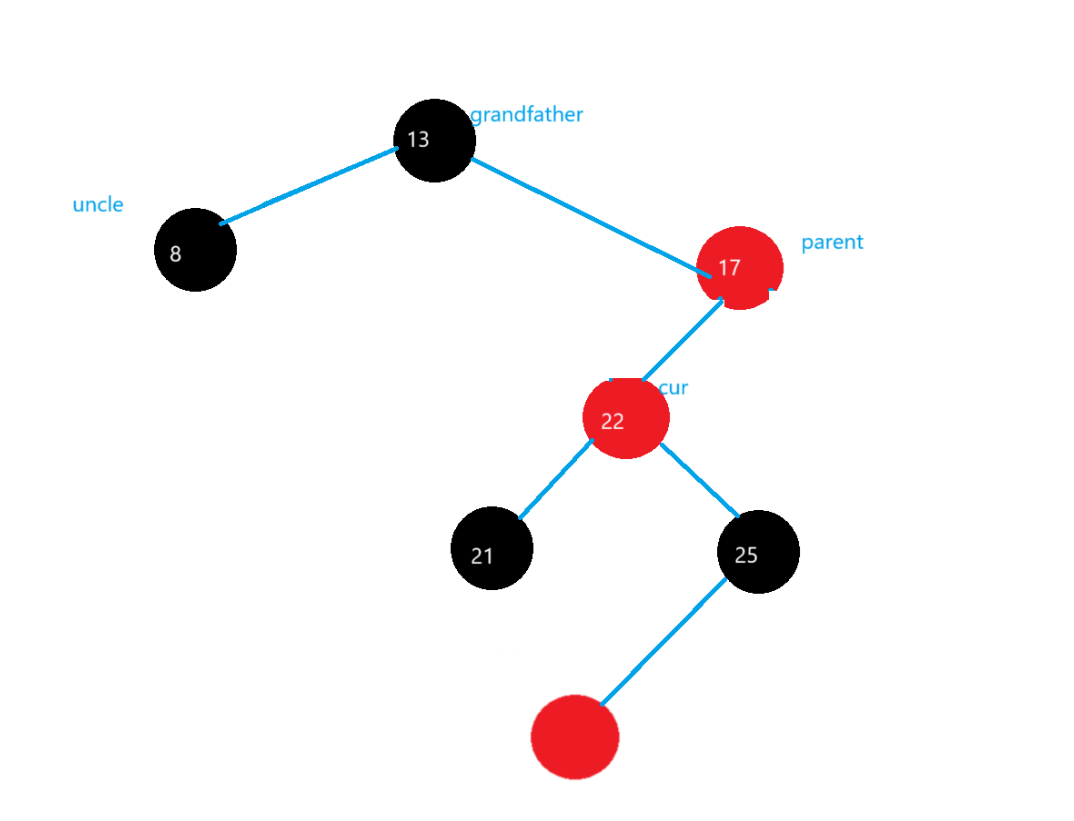
首先要在parent進行右旋操作

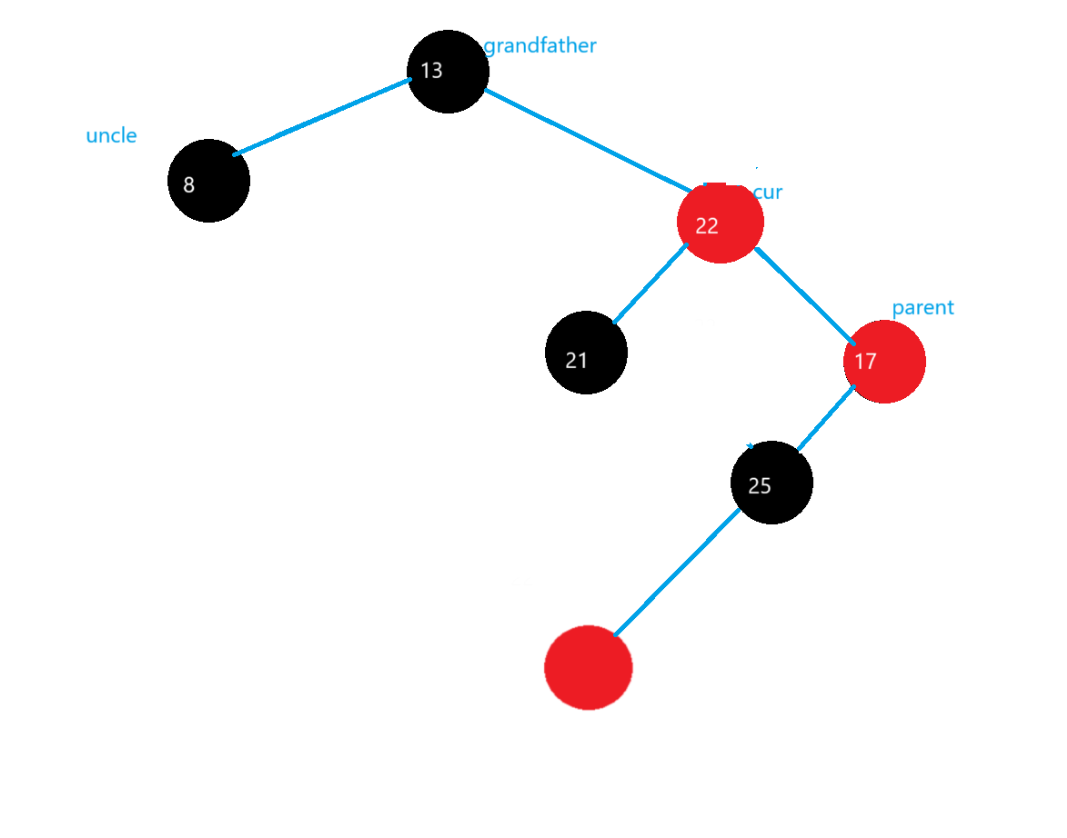
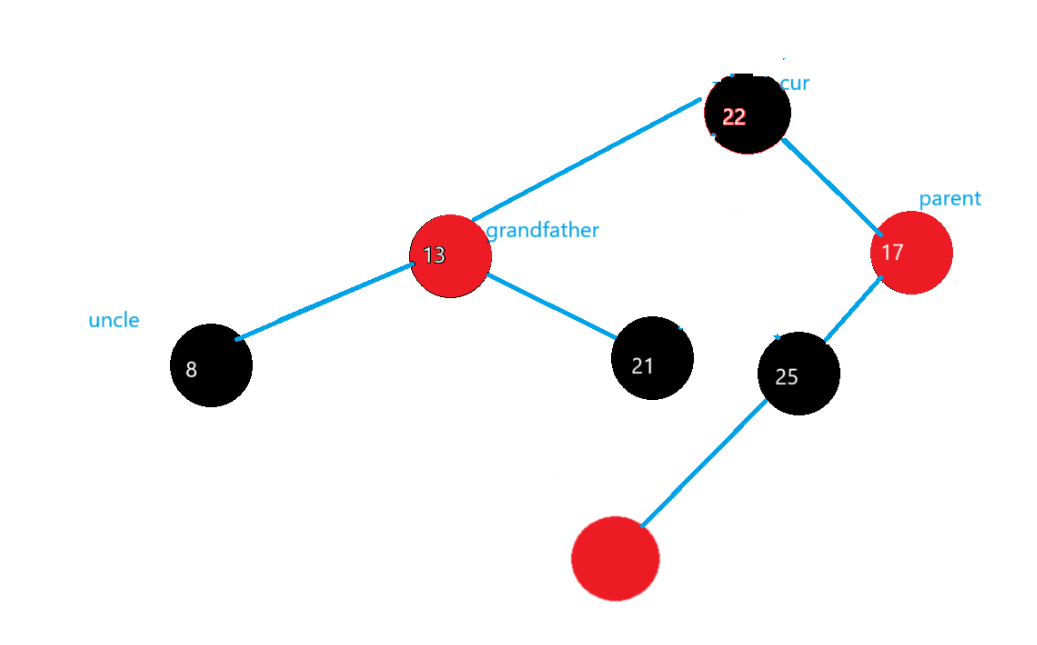
再對grandparent進行左旋，讓grandfather的顏色變紅，cur的顏色變黑

代碼：

現在給出對應部分代碼，左旋，右旋，左右旋，右左旋代碼也在最后的完整代碼中

if (cur == parent->_right)
{RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;
}
else
{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;
}
break;

四、紅黑樹檢查代碼

1.通過遞歸得出高度的代碼

int Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

2.根據紅節點的父親是否是紅色來判斷紅黑樹是否有誤

//為什么不是int & blacknum，因為要利用棧幀，保存當前形式下，blackanum的值
bool CheckColour(Node* root, int blacknum,int benchmark)
{if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent &&root->_parent->_col == RED){cout << root->_kv.first << "出現連續紅色節點" << endl;return false;}return CheckColour(root->_left,blacknum,benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}

3.利用左邊的那條支路創建黑高的基準值，再在checkcolour把所有節點黑高節點檢查一遍得出結果

bool IsBalance()
{return IsBalance(_root);
}
bool IsBalance(Node* root)
{if (root == nullptr)return true;if (root->_col != BLACK)return false;
//	return CheckColour(root);//基準值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++benchmark;  }//這里是以最左路徑為標準cur = cur->_left;}return  CheckColour(root, 0, benchmark);
}

五、總代碼

1.RBTree.h

#pragma once
#include<iostream>
#include<stdio.h>
using namespace std;enum Colour
{RED,BLACK
};
template<class K,class V> 
struct RBTreeNode
{//三叉鏈RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V> & kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){//Node* parent = cur;if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else if (parent->_kv.first > kv.first){parent->_left = cur;}cur->_parent = parent;while (parent&&parent->_col==RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且為紅if (uncle && uncle->_col == RED){//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;//grandfather = parent->_parent; }else//uncle不存在或uncle存在且為黑{//這是什么意思？這里我自己判斷了if (cur == parent->_left ){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED; }break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;//grandfather = parent->_parent;}else{//我覺得案按理來說得判斷，這是叔叔不存在的情況？if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){//這是AVL樹第一集的末尾了Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){//這是AVL樹第一集的末尾了Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright){curright->_parent = parent;}Node* ppnode = parent->_parent;cur->_right = parent;//Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_right == parent){ppnode->_right = cur;}else{ppnode->_left = cur;}cur->_parent = ppnode;}}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;//int bf = cur->_left->_bf;RotateR(parent->_right);RotateL(parent);}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;//	int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}//為什么不是int & blacknum，因為要利用棧幀，保存當前形式下，blackanum的值bool CheckColour(Node* root, int blacknum,int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent &&root->_parent->_col == RED){cout << root->_kv.first << "出現連續紅色節點" << endl;return false;}return CheckColour(root->_left,blacknum,benchmark)&& CheckColour(root->_right, blacknum, benchmark);}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;if (root->_col != BLACK)return false;//	return CheckColour(root);//基準值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++benchmark;  }//這里是以最左路徑為標準cur = cur->_left;}return  CheckColour(root, 0, benchmark);}
private:Node* _root = nullptr;
};

2.Test.c代碼

插入10000個隨機數進行測試

#include"RBTree.h"
#include<vector>
#include<time.h>
//int main()
//{
//	int a[] = { 4,2,6,1,3,5,15,7,16,14 };
//	RBTree<int, int> t;
//	for (auto e : a)
//	{
//		t.Insert(make_pair(e, e));
//		cout << "Insert:" << e << "->"<<t.IsBalance() << endl;
//	}
//	return 0;
//}int main()
{const int N = 10000;vector<int> v;v.reserve(N);srand(time(0));for (int i = 0;i < N;i++){v.push_back(rand());}RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;}return 0;
}

謝謝觀眾老爺的觀看！！！

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/89726.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/89726.shtml
英文地址，請注明出處：http://en.pswp.cn/web/89726.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

【黃山派-SF32LB52】—硬件原理圖學習筆記

【黃山派-SF32LB52】—硬件原理圖學習筆記

目錄 一、硬件介紹 二、芯片主控 1.模組介紹 2.原理圖介紹 3.模組供電電路 三、電源轉換部分 1.OVP過壓保護電路 2.CHG充電電路 3.系統電源橋接電路 4.LDO電路 四、Debug電路 1.一鍵下載電路 五、QSPI屏幕 六、SD卡 七、AUDIO音頻 八、GPIO電路 1.按鍵部分…
閱讀更多...
從五次方程到計算機：數學抽象如何塑造現代計算

從五次方程到計算機：數學抽象如何塑造現代計算

引言 數學的發展往往始于一個具體的問題&#xff0c;而后在尋求解答的過程中&#xff0c;催生出深刻的抽象理論。從五次方程的求解到抽象代數&#xff0c;再到范疇論和λ演算&#xff0c;最終影響圖靈機和現代計算機的設計&#xff0c;這一歷程展現了數學如何從實際問題演變為通…
閱讀更多...
劇本殺小程序開發：科技賦能，重塑推理娛樂新形態

劇本殺小程序開發：科技賦能，重塑推理娛樂新形態

在科技飛速發展的今天&#xff0c;各個行業都在積極探索與科技的融合&#xff0c;以實現創新發展。劇本殺行業也不例外&#xff0c;劇本殺小程序的開發&#xff0c;正是科技賦能傳統娛樂的生動體現&#xff0c;它重塑了推理娛樂的新形態&#xff0c;為玩家帶來了前所未有的游戲…
閱讀更多...
機器學習sklearn入門：歸一化和標準化

機器學習sklearn入門：歸一化和標準化

bg&#xff1a;歸一化&#xff08;Normalization&#xff09;通常指將數據按比例縮放至某個特定范圍&#xff0c;但具體范圍并不一定是固定的 0到1。標準化是將數據轉換成均值為0&#xff0c;標準差為1的分布。使用場景&#xff1a;用歸一化&#xff1a;需要嚴格限定范圍&#…
閱讀更多...
【Project】kafka+flume+davinci廣告點擊實時分析系統

【Project】kafka+flume+davinci廣告點擊實時分析系統

一、項目需求分析 某電商平臺需實現廣告實時點擊分析系統&#xff0c;核心需求為實時統計以下內容的Top10&#xff1a; 各個廣告的點擊量各個省份的廣告點擊量各個城市的廣告點擊量 通過實時掌握廣告投放效果&#xff0c;為廣告投放策略調整和大規模投入提供依據&#xff0c;以…
閱讀更多...
JAVA后端開發——success(data) vs toAjax(rows): 何時用

JAVA后端開發——success(data) vs toAjax(rows): 何時用

toAjax(int rows)用途&#xff1a;用于不返回任何數據的 “寫” 操作&#xff08;增、刪、改&#xff09;。工作原理&#xff1a;它只接收一個 int 類型的參數&#xff08;通常是數據庫操作影響的行數&#xff09;。它只關心這個數字是不是大于0&#xff0c;然后返回一個通用的…
閱讀更多...
pdf格式怎么提取其中一部分張頁？

pdf格式怎么提取其中一部分張頁？

想從PDF里提取幾個頁面&#xff0c;辦法還挺多的&#xff0c;下面給你嘮嘮常見的幾種&#xff0c;保準你一看就懂。一、用專業PDF編輯軟件提取 像Adobe Acrobat&#xff0c;這可是PDF編輯界的“老手”了。你先把要處理的PDF文件在Adobe Acrobat里打開&#xff0c;接著找到菜單欄…
閱讀更多...
Spring監聽器

Spring監聽器

1、監聽器的原理 ApplicationListener<T>是Spring框架中基于觀察者模式實現的事件監聽接口&#xff0c;用于監聽應用程序中特定類型的事件。該接口是一個函數式接口&#xff0c;從Spring 4.2開始支持Lambda表達式實現。 接口定義如下&#xff1a; FunctionalInterface …
閱讀更多...
基于Rust游戲引擎實踐（Game）

基于Rust游戲引擎實踐（Game）

Rust游戲引擎推薦 以下是一些流行的Rust游戲引擎，適用于不同開發需求： Bevy 特點：數據驅動、模塊化設計，支持ECS架構，適合初學者和復雜項目。 適用場景：2D/3D游戲、原型開發。 Amethyst 特點：成熟的ECS框架，支持多線程，社區活躍。 適用場景：大型游戲或高性能應用。…
閱讀更多...
PyTorch 數據加載實戰：從 CSV 到圖像的全流程解析

PyTorch 數據加載實戰：從 CSV 到圖像的全流程解析

目錄 一、PyTorch 數據加載的核心組件 1.1 Dataset 類的核心方法 1.2 DataLoader 的作用 二、加載 CSV 數據實戰 2.1 自定義 CSV 數據集 2.2 使用 TensorDataset 快速加載 三、加載圖像數據實戰 3.1 自定義圖像數據集 3.2 使用 ImageFolder 快速加載 四、加載官方數據…
閱讀更多...
程序人生，開啟2025下半年

程序人生，開啟2025下半年

時光匆匆&#xff0c;2025年已然過去一半。轉眼來到了7月份。 回望過去上半年&#xff0c;可能你也經歷了職場的浮沉、生活的跌宕、家庭的變故。 而下半年&#xff0c;生活依舊充滿了各種變數。 大環境的起起伏伏、生活節奏的加快&#xff0c;都讓未來的不確定性愈發凸顯。 在這…
閱讀更多...
在 .NET Core 中創建 Web Socket API

在 .NET Core 中創建 Web Socket API

要在 ASP.NET Core 中創建 WebSocket API&#xff0c;您可以按照以下步驟操作&#xff1a;設置新的 ASP.NET Core 項目打開 Visual Studio 或您喜歡的 IDE。 創建一個新的 ASP.NET Core Web 應用程序項目。 選擇API模板&#xff0c;因為這將成為您的 WebSocket API 的基礎。在啟…
閱讀更多...
Python 之地址編碼識別

Python 之地址編碼識別

根據輸入地址&#xff0c;利用已有的地址編碼文件&#xff0c;構造處理規則策略識別地址的編碼。 lib/address.json 地址編碼文件&#xff08;這個文件太大&#xff0c;博客里放不下&#xff0c;需要的話可以到 gitcode 倉庫獲取&#xff1a;https://gitcode.com/TomorrowAndT…
閱讀更多...
kafka的部署

kafka的部署

目錄 一、kafka簡介 1.1、概述 1.2、消息系統介紹 1.3、點對點消息傳遞模式 1.4、發布-訂閱消息傳遞模式 二、kafka術語解釋 2.1、結構概述 2.2、broker 2.3、topic 2.4、producer 2.5、consumer 2.6、consumer group 2.7、leader 2.8、follower 2.9、partition…
閱讀更多...
小語種OCR識別技術實現原理

小語種OCR識別技術實現原理

小語種OCR&#xff08;光學字符識別&#xff09;技術的實現原理涉及計算機視覺、自然語言處理&#xff08;NLP&#xff09;和深度學習等多個領域的融合&#xff0c;其核心目標是讓計算機能夠準確識別并理解不同語言的印刷或手寫文本。以下是其關鍵技術實現原理的詳細解析&#…
閱讀更多...
GPT：讓機器擁有“創造力”的語言引擎

GPT：讓機器擁有“創造力”的語言引擎

當ChatGPT寫出莎士比亞風格的十四行詩&#xff0c;當GitHub Copilot自動生成編程代碼&#xff0c;背后都源于同一項革命性技術——**GPT&#xff08;Generative Pre-trained Transformer&#xff09;**。今天&#xff0c;我們將揭開這項“語言魔術”背后的科學原理&#xff01;…
閱讀更多...
LeetCode｜Day19｜14. 最長公共前綴｜Python刷題筆記

LeetCode｜Day19｜14. 最長公共前綴｜Python刷題筆記

LeetCode&#xff5c;Day19&#xff5c;14. 最長公共前綴&#xff5c;Python刷題筆記 &#x1f5d3;? 本文屬于【LeetCode 簡單題百日計劃】系列 &#x1f449; 點擊查看系列總目錄 >> &#x1f4cc; 題目簡介 題號&#xff1a;14. 最長公共前綴 難度&#xff1a;簡單…
閱讀更多...
安全事件響應分析--基礎命令

安全事件響應分析--基礎命令

----萬能密碼oror1 or # 1or11 1 or 11安全事件響應分析------***windoes***------方法開機啟動有無異常文件 【開始】?【運行】?【msconfig】文件排查 各個盤下的temp(tmp)相關目錄下查看有無異常文件 &#xff1a;Windows產生的 臨時文件 可以通過查看日志且通過篩…
閱讀更多...
基于C#+SQL Server實現（Web）學生選課管理系統

基于C#+SQL Server實現（Web）學生選課管理系統

學生選課管理系統的設計與開發一、項目背景學生選課管理系統是一個學校不可缺少的部分&#xff0c;傳統的人工管理檔案的方式存在著很多的缺點&#xff0c;如&#xff1a;效率低、保密性差等&#xff0c;所以開發一套綜合教務系統管理軟件很有必要&#xff0c;它應該具有傳統的…
閱讀更多...
垃圾回收(GC)

垃圾回收(GC)

內存管理策略&#xff0c;在業務進程運行的過程中&#xff0c;由垃圾收集器以類似守護協程的方式在后臺運行&#xff0c;按照指定策略回收不再被使用的對象&#xff0c;釋放內存空間進行回收 優勢&#xff1a; 屏蔽內存回收的細節&#xff1a;屏蔽復雜的內存管理工作&#xff0…
閱讀更多...
最新文章

Copyright @ 2022~2023