?主要內容

·模擬與數字

·周期模擬信號

·數字信號

·傳輸減損

·數據速率限制

·性能

注：數據必須被轉換成電磁信號才能進行傳輸。

一、模擬與數字

? ? ? ? 數據以及表示數據的信號可以使用模擬或者數字的形式。數據可以是模擬的也可以是數字的，模擬數據是連續的采用連續值；數字數據有離散狀態，采用離散值。

? ? ? ? 信號可以是模擬的也可以是數字的，模擬信號在一個范圍內可以有無窮多個數值（強度等級），而數字信號只能有有限個值。

圖3.1 ? 模擬信號和數字信號的比較?

? ? ? ? 模擬信號和數字信號可以是周期的或非周期的，在數據通信中，通常使用周期模擬信號和非周期數字信號。

二、周期模擬信號

? ? ? ? 周期模擬信號可以分為簡單類型或復合類型兩種。

? ? ? ? 簡單類型模擬信號，即正弦波（sine wave），不能再分解為更簡單的信號，而復合型模擬信號則是由多個正弦波信號組成的。

? ????????決定正弦波的三個參數：峰值振幅、頻率和相位。

圖 3.2 ?正弦波?

? ? ?

例3.1：

????????家用電源的功率可以用峰值振幅為155V到170V的正弦波表示。但是，大家都知道美國家用的電壓是110V到120V。不一樣的原因在于這些均方根(rms)值。信號平方后再計算平均振幅。峰值等于 2? × rms。

圖 3.3 ?相位和頻率相同但振幅不同的兩個信號?

圖 3.4 ?振幅和相位相同但頻率不同的兩個信號?

?例3.3：

????????家用電的頻率是60Hz，這個正弦波的周期就可以確定如下：

例3.4：

????????用微秒表示周期為100ms。

例3.5：

????????一個信號的周期是100ms。那么它以千赫為單位表示的頻率是多少？?

????????相位描述了波形相對于時間0的位置。?

圖 3.5 ?振幅和頻率相同但相位不同的正弦波

?例3.6：

????????正弦波相對于0時刻的偏移量是1/6周期，相位的角度值和弧度值是多少？

圖 3.6 ?波長和周期

? ? ? ? ?波長與周期之間的關系：

波長 = 傳播速度 × 周期

圖 3.7 ?正弦波的時域圖和頻域圖

????????用頻域圖中單個峰值可表示時域圖中一個完整正弦波。?

例3.7：

????????當我們處理多個正弦波時，頻域更簡潔更有用。 ?例如，圖3.8顯示了三個不同振幅和頻率的正弦波，它們通過頻域中的三個尖峰表示。

圖 3.8 ?三個正弦波的時域和頻域?

? ? ? ? 單一頻率的正弦波在數據通信中沒有用處，我們需要發送復合信號，復合信號由許多簡單正弦波組成。按照傅里葉分析，任何復合信號都是由具有不同頻率、相位和振幅的簡單正弦波組合而成的。?

? ? ? ? 如果復合信號是周期性的，分解得到的是一系列具有離散頻率的信號；如果復合信號是非周期性的，分解得到的是具有連續頻率的正弦波組合。

例3.8：

????????圖3.9顯示了頻率為f的周期復合信號。這種信號不是數據通信中的典型信號。我們可以把它看成三個告警系統，每一個有不同的頻率。這個信號的分析可以讓我們理解如何分解信號。

圖 3.9 ?復合周期信號

圖 3.10 ?復合周期信號在時域和頻域中的分解（f為基礎頻率/第一諧波）?

例3.9：

????????圖3.11表示了一個非周期復合信號。它可以在一個或兩個詞發音時由麥克風或電話機產生。這種情況下，復合信號不可能是周期的，因為我們不可能以完全相同的音調重復相同的詞或語句。

圖 3.11 ?非周期信號的時域和頻域

????????信號的帶寬是信號最高頻率與最低頻率的差值。?

?圖 3.12 ?周期復合信號和非周期復合信號的帶寬

?例3.10：

????????如果一個周期信號分解為5個正弦波信號，頻率分別為100，300，500，700和900Hz，那么其帶寬是多少？假定所有分量的最大振幅都為10V，試畫出該信號的頻譜。

解： 設 fh 為最高頻率，fl 為最低頻率，B為帶寬，則：

? ? ? ?

頻譜只有5個尖峰，分別位于100，300，500，700和900Hz的位置（見圖3.13）。

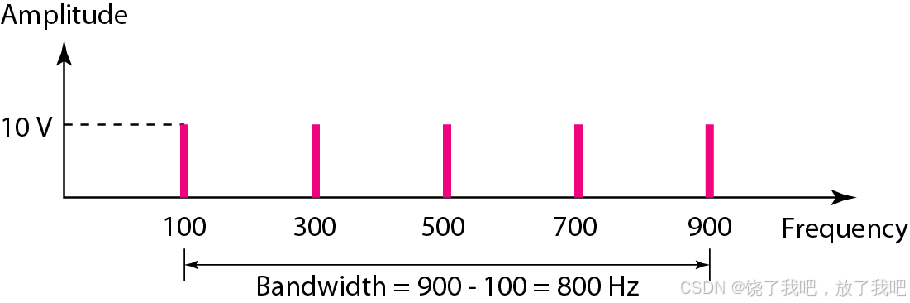
圖 3.13 ?例3.10的帶寬

例3.11

????????一個周期信號的帶寬是20Hz，其最高頻率是60Hz，最低頻率是多少？如果信號包含具有相同振幅的所有整數頻率，試畫出其頻譜。

解： 設 fh 為最高頻率，fl 為最低頻率，B為帶寬，則：?

?頻譜包含所有整數頻率。用一系列尖峰表示（見圖3.14）。

圖 3.14 ?例3.11的帶寬

例3.15?

????????非周期復合信號的另一個例子是老式模擬黑白電視接收的信號。電視屏幕由像素組成。如果我們假定分辨率為525×700，那么每個屏幕就會有367,500個像素。如果屏幕每秒掃描30次，每秒就是367,500×30= 11,025,000個像素。最壞的情況是黑色像素和白色像素交替。每個周期我們能發送兩個像素。因此，每秒我們需要11,025,000 / 2 = 5,512,500個周期（或Hz）。所需的帶寬是5.5125 MHz。

三、數字信號

? ? ? ? 數據除了可以用模擬信號表示外，還可以使用數字信號表示。例如，1可以編碼成正電平，0可以編碼為零電平。一個數字信號有多個電平，那每個電平就可以發送多位。

圖 3.16 ?兩個數字信號：一個有兩個電平而另一個有四個電平

?例3.16：

????????一個數字信號有8個電平，那么每個電平需要多少個位表示？我們根據下面公式進行計算：

得到每個信號電平用3位表示。?

例3.17：

????????一個數字信號有9個電平，問每個電平可表示多少位？我們根據公式計算，得出每個信號電平用3.17個位表示。但是，這個答案是不現實的。每個電平發送的位數必須是整數并且是2的冪。這個例子中，4位用來表示一個電平。

例3.18：

????????假定一頁平均24行，每一行80個字符，假定每個字符需要8位，我們需要每分鐘100頁的速率下載文本文檔，所需的通道比特率（每秒鐘發送的位數bps）是多少？

解:

100×24×80×8/60 = 1536000/60 bps=25600bps

例3.19：

????????數字化語音通道是通過數字化4kHz帶寬的模擬語音信號形成的。我們需要以最高頻率的2倍對信號進行采樣（即每赫茲兩個樣本）。我們假定每個樣本需要8位，那么所需的比特率是多少？

解：

例3.20：

????????HDTV使用數字信號廣播高質量視頻信號。HDTV屏幕通常為16:9，每屏有1920×1080 個像素，每秒刷新30次，24位代表一種顏色像素。高清晰電視（HDTV）的比特率是多少?

解：

注

1、基于傅里葉分析，數字信號是復合模擬信號，帶寬無窮大；

2、傅里葉分析可以用來分解數字信號；

3、如果數字信號是周期性的，分解后的信號可以表示為無窮大帶寬和離散頻率的頻域（圖3.17）；

4、如果數字信號是非周期性的，分解后的信號仍然是無窮大帶寬，但頻率是連續的（圖3.17）。

圖 3.17 ?周期數字信號和非周期數字信號的時域和頻域?

數字信號的傳輸

????????數字信號是無窮大帶寬的復合模擬信號，有兩種傳輸方式：基帶傳輸和寬帶傳輸（使用調制）。

????????基帶傳輸（以信號本身的頻譜進行傳輸）：通過通道發送數字信號，該信號不轉換成模擬信號，它需要一個帶寬下限頻率為0的低通通道（帶寬從頻率0開始）。

????????寬帶傳輸：把數字信號轉換成模擬信號進行傳輸，允許使用帶通通道，即帶寬不從頻率0開始的通道。

基帶傳輸

????????帶寬只組成一條通道的專用介質，例如連接兩臺計算機的電纜。

圖 3.18 ?基帶傳輸

圖 3.19 ?兩條低通通道的帶寬

圖 3.20使用專用介質的基帶傳輸

????????只有我們有無窮大或非常大帶寬的低通通道，保持數字信號形狀的數字信號基帶傳輸才是可能的。?

例3.21：

????????專用通道（介質的整個帶寬用于一條單通道）的一個例子是LAN。幾乎現在的每一個有線LAN使用專用通道用于兩個站之間的互相通信。在多點連接的總線拓撲結構LAN中，每個時刻只有兩個站可以互相通信（時間共享），而其他站限制發送數據。在星型拓撲結構LAN中，每個站和集線器（或交換機）之間的整個通道用于這兩個實體間的通信。

有限帶寬的低通通道

????????把數字信號近似成模擬信號，近似程度取決于可用的帶寬。

????????大致近似（最小帶寬）：

????????????????假定數字信號比特率為N，用模擬信號來大致近似這個信號；

????????????????最壞情況，即數字信號中變化的最大數：01010101…或10101010…，需要的頻率f = N/2；

????????????????最好情形：0000…或1111…，需要的頻率為0；

????????????????所需帶寬為N/2；

為了更好近似，可以增加更多諧波，所需帶寬相應增加。

?圖 3.21 ?對于最壞情形的數字信號使用一個諧波的大致近似

圖 3.22 ?更好近似：使用三個諧波（1/3/5）模擬數字信號

????????基帶傳輸中，所需的帶寬與比特率成正比；如果我們需要更快地發送位，我們就需要更大的帶寬。?

表 3.2 ?帶寬需求量

例3.22：

????????如果我們需要使用基帶傳輸發送 1Mbps，那么低通通道所需的帶寬是多少？

解：

答案取決于所需的準確性。

????????a. 最小帶寬、大致近似時，B = 比特率/2，即500 kHz。 ?

????????b. 使用第一和第三諧波可以得到更好的結果，所需帶寬是B = 3 × 500 kHz = 1.5 MHz。

????????c. 使用第一、第三和第五諧波仍然可以得到更好的結果，所需帶寬是 B = 5 × 500 kHz = 2.5 MHz。?

例3.23：

????????我們有一條帶寬為100kHz的低通通道，那么這條通道的最大比特率是多少？

解： 如果我們使用第一諧波可以得到最大比特率，比特率是2倍有效帶寬，即200kbps。

寬帶傳輸

圖 3.23 ?帶通通道的帶寬

????????如果可用通道是帶通通道，我們不能直接發送數字信號到通道；我們需要在傳輸前把數字信號轉換成模擬信號。

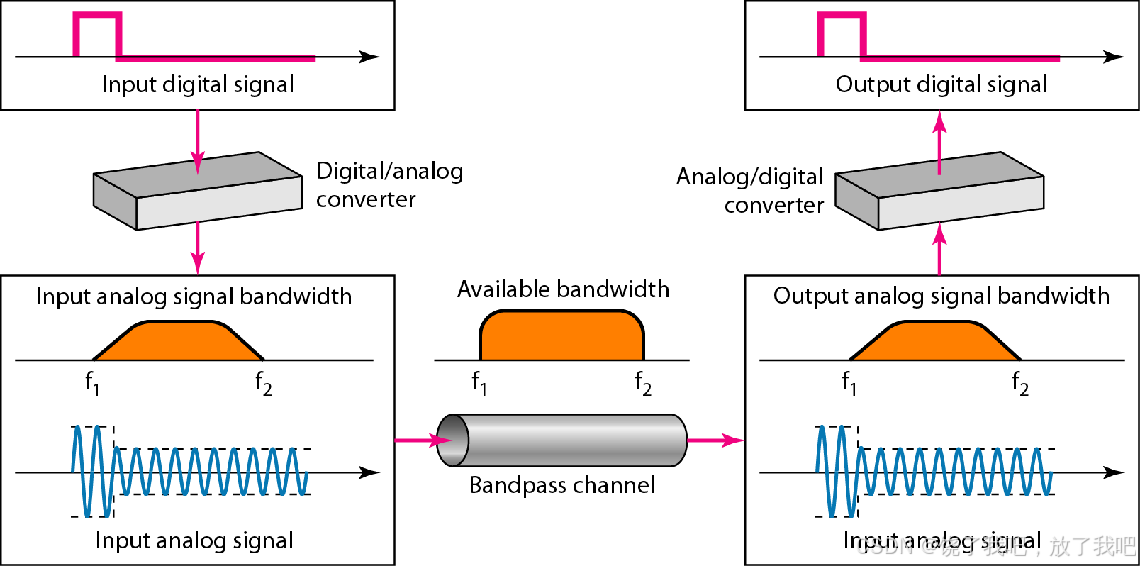
圖 3.24 ?數字信號在帶通通道傳輸的調制過程

例3.24：

????????使用調制的寬帶傳輸的一個例子是通過電話用戶線傳輸計算機數據，電話用戶線連接住所到中心電話局。這些線路設計用有限帶寬承載語音。這個通道通常被看做帶通通道。我們從計算機把數字信號轉換成模擬信號，然后發送模擬信號。我們要安裝兩個轉換器用來在發送端把數字信號轉換成模擬信號以及在接收端把模擬信號轉換回數字信號。

例3.25：

????????數字蜂窩電話——為了更好地接收，數字蜂窩電話把模擬信號轉換成數字信號（見第16章）。雖然分配給公司提供數字蜂窩電話服務的帶寬很廣，但是我們不能不經轉換發送數字信號。原因是，我們在主叫方和被叫方之間只有一條可用的帶通通道。我們需要在發送前把數字信號轉換成復合模擬信號。?

四、傳輸減損

????????信號通過介質進行傳輸，但是其傳輸并非是完美無缺的，不完美的地方導致了信號減損，這意味著信號在介質的開始一端和結束一端是不相同的，接收到的信號并非就是發出的信號。

???????? 通常會發生三種類型的減損：衰減、失真和噪聲。

衰減

圖 3.26 ?衰減（失去一些能量克服介質的阻抗，發熱）

分貝

????????為了說明信號損失或增益的強度，工程上使用分貝的概念； 分貝（decibel，dB）用于計算兩種信號之間或者同一信號在兩個不同位置之間的相對強度：

dB = 10log10(P2/P1)

P1和P2分別是信號在位置1和位置2的功率

例3.26：

????????假設信號通過一種傳輸介質傳輸后，它的功率降低了一半。這可以表示為P2=(1/2)P1，這種情況下衰減（損失的能量）可以計算為：

因此，–3dB（分貝）或者3dB衰減等價于功率損失了一半。

例3.27：

????????假定信號通過一個放大器，它的功率增大為原來的10倍。這表示P2=10P1。在這種情況下，放大量（功率增益）可以計算為：

例3.28：

????????工程人員使用分貝來計算信號強度變化的原因之一是，當涉及計量多處（級聯）而不僅僅是兩處的信號強度時，分貝數可以相加（或相減）。在圖3.27中，一個信號從位置1傳輸到位置4，在這種情況下，分貝可以計算為：?

圖 3.27 ?例3.28的分貝?

例3.29:

????????有時候分貝用來以毫瓦計量信號功率。這種情況下，它成為dBm，計算為dBm = 10log10Pm , 這里Pm是以毫瓦為單位的功率。如果信號的dBm=?30，計算它的功率。 解： 我們計算信號的功率如下：

例3.30:

????????電纜中的損耗一般定義為每公里分貝數（dB/km）。如果電纜每公里分貝數為?0.3dB/km，信號在電纜開始端的功率為2mW，則在5km處信號的功率是多少？

解： 電纜中的損耗為5×(?0.3) = ?1.5 dB。我們計算功率如下：

失真

????????失真意味著信號改變了形態或形狀。導向媒體上信號傳播速度隨頻率的不同而改變，所以 各信號成分延遲的差異會產生相位的差異，即接收方的信號成分與發送方的信號成分存在相位差異。

?圖 3.28 ?失真

噪聲

熱噪聲：電纜中的電子隨機移動產生的額外信號

?感應噪聲：來源于發動機和設備（工作時相當于發射天線）

串擾：電纜之間的相互影響

脈沖噪聲：一種尖峰信號，來自輸電線、閃電等?

圖 3.29 ?噪聲

信噪比SNR（signal-to-noise ratio）?

????????信噪比：信號功率與噪聲功率的比率，較高意味著信號較少的被噪聲破壞，較低意味著被噪聲較多的破壞。

SNR = 平均信號功率/平均噪聲功率

以分貝描述：SNR dB = 10log10SNR

例3.31：

????????對于無噪聲通道的SNR和SNRdB是：

注：我們在現實中不會得到這樣的比率，它是理論上的。?

?圖 3.30 ?SNR的兩種情形: 高 SNR和低 SNR

五、數據速率限制

????????數據通信中一個非常重要的問題是：在一個通道中能夠以多快的速率發送數據，即每秒鐘的比特數。數據速率取決于：有效帶寬、使用信號的電平數、通道的質量。

? ? ? ? 為計算數據速率，有兩個理論上的定理或公式：

????????????????無噪聲通道：奈奎斯特定理

????????????????噪聲通道：香農容量公式

奈奎斯特定理

????????對于無噪聲通道，奈奎斯特定理定義了理論上的最大比特率：

比特率 = 2×帶寬×log2L

其中，帶寬指通道的帶寬，L表示信號電平的個數

?注：增加信號電平數會增加接收方的負擔，減弱系統的可靠性。

例3.32：

????????奈奎斯特公式是否適用于基帶傳輸中描述的直覺上的比特率？

解： 當只有兩個電平時它們匹配。我們說，在基帶傳輸中，如果我們在最壞情況只使用第一諧波，那么比特率是2倍帶寬。但是，奈奎斯特公式比我們直覺上得到的更通用，它可以應用到基帶傳輸和調制，也可以應用到有兩個或多個信號電平的情況。

例3.33：

????????考慮帶寬為3000Hz的無噪聲通道，傳輸兩種電平的信號，則最大比特率計算為：

例3.34：

????????考慮同樣的無噪聲通道，傳輸具有四種信號電平的信號（每一種電平發送兩個位），最大比特率可以計算為：

例3.35：

????????通過帶寬為20kHz的無噪聲通道發送265kbps，我們需要多少個信號電平？ 解： 我們使用奈奎斯特公式如下:

?????????因為結果不是2的冪，所以我們需要增加電平數或者減小比特率。如果我們有128個電平，比特率是280kbps；如果我們有64個電平，比特率是240kbps。

香農容量公式

????????對于噪聲通道，香農容量公式定義了理論上的最高數據速率。

通道容量 = 帶寬×log2(1+SNR)

其中，帶寬指通道的帶寬，SNR是信噪比

注意：公式沒有指出信號電平數，定義了通道特性。

例3.36：

????????考慮一個極端的噪聲通道，其信噪比的值接近于0。換句話說，噪聲很強而信號很弱，對于該通道，其容量C計算為：

這意味著通道的容量為0，與帶寬無關。換句話說，通過該通道不能接收到任何數據。?

例3.37：

????????我們可以計算一條常規電話線路理論上的最高比特率。通常情況下，電話線路的帶寬為3000Hz，信噪比通常為3162。對于這一通道，其容量計算為：

????????這表示電話線路的最高比特率是34,860bps。如果要使數據發送速率比這更快，則可增大線路的帶寬或者提高信噪比。?

例3.38：

????????信噪比通常以分貝給定。假定SNRdB = 36，通道帶寬是2MHz。理論上的通道容量計算為：

例3.39：

????????為了實際操作方便，當SNR很大時，假定SNR + 1幾乎與SNR相等，理論通道容量可以簡化為：?

例如，我們可以計算前一例子的理論容量為：?

例3.39推導過程

例3.40-使用兩種限制條件：

????????有一個1MHz帶寬的通道，通道的信噪比是63，合適的比特率以及信號電平是多少？

解： 首先，使用香農公式確定上限：?

????????盡管香農公式計算結果是6Mbps，但這是上限。為了獲得更好的性能，可選擇低一些的值，如4Mbps。然后使用奈奎斯特公式計算信號電平的數量：?

注：香農容量公式給出數據速率的上限，奈奎斯特定理給出所需的信號電平數。?

六、性能?

????????網絡中的一個重要問題是網絡的性能—網絡怎么算好？衡量性能的技術術語：

·帶寬：以赫茲或比特率表示

·吞吐量：發送速度快慢的實際衡量值，小于帶寬

·延遲：第一個比特從源開始發出到整個報文完全到達目標所經歷的時間，包括傳播時間（指一個比特從源端到達目標端所需要的時間，等于：距離/信號傳播速度）、傳輸時間（指源端將整個報文傳輸出去需要的時間，等于：報文長度/帶寬）、排隊時間和處理延遲

·帶寬與延遲的乘積：定義了充滿鏈路的位數

·抖動：不同分組有不同的延遲，某些應用敏感

帶寬

????????在網絡中，我們在兩種情況下使用術語帶寬： 第一種，以赫茲衡量的帶寬指復合信號包含的頻率范圍或者通道能通過的頻率范圍； 第二種，以每秒比特數衡量的帶寬指通道或鏈路中位傳輸的速率。

例3.41：

????????用于語音或數據的用戶線帶寬是4kHz。使用復雜的調制解調器把數字信號轉換成模擬信號，這種線路用于數據傳輸的帶寬可以達到56,000bps。

例3.42：

????????如果電話公司提高線路的質量，把帶寬增加到8kHz，通過例3.42提到的相同技術，可以發送 112,000bps。

吞吐量

例3.43

????????帶寬為10Mbps的網絡每分鐘只能平均傳輸12,000個幀，每個幀平均攜帶10,000個位。那么這個網絡的吞吐量是多少？

解： 我們可以計算吞吐量為：

注：這個例子中的吞吐量幾乎是帶寬的五分之一。?

例3.44

????????如果兩點之間的距離是12,000km，傳播時間是多少？假定電纜中的傳播速度是2.4×108 m/s。 解： 我們可以計算傳播速度為：

注：這個例子說明如果源和目標之間有直接電纜，一個位經過大西洋只需要50ms。?

例3.45：

????????如果網絡的帶寬是1Gbps，那么2500個字節的報文（一封電子郵件）的傳播時間和傳輸時間是多少？假定發送方和接收方之間的距離是12,000km，光以速度2.4×108m/s傳輸。 解： 我們計算傳播時間和傳輸時間為：

注：在這個例子中，因為報文較短而帶寬較高，主導因素是傳播時間而不是傳輸時間，傳輸時間可忽略不計。

例3.46：

????????如果網絡帶寬是1Mbps，那么5M字節的報文（一張圖像）的傳播時間和傳輸時間是多少？假定發送方和接收方之間的距離是12,000km，以速度2.4×108m/s傳輸 解： 我們計算傳播時間和傳輸時間為：?

注：因為報文較長而帶寬不是很高，所以主導因素是傳輸時間而不是傳播時間，傳播時間可以忽略不計。?

延遲

圖 3.31 ?在情形1中用位充滿鏈路?

圖 3.32 ?在情形2下用位充滿鏈路

帶寬與延遲的乘積

例3.48：

????????我們把兩點間的鏈路看做管道。管道的橫截面表示帶寬，管道的長度表示延遲。我們可以說管道的容量定義了帶寬延遲乘積，如下圖所示。

帶寬延遲乘積定義了能充滿鏈路的位數。?