??學習率調度作為模型優化的重要方法，也集成在了PyTorch的 optim模塊中。我們可以通過下述代碼將學習率調度模塊進行導入。

from torch.optim import lr_scheduler

??接下來，我們從較為基礎的學習率調度方法入手，熟悉PyTorch中實現學習率調度的基本思路與流程。

一、優化器與狀態字典（state_dict）

??在此前的模型訓練過程中，我們已經基本了解了PyTorch中的模型優化器的基本使用方法。模型優化器是求解損失函數的函數，其中包含了模型訓練的諸多關鍵信息，包括模型參數、模型學習率等，同時在進行模型訓練時，我們也是通過優化器調整模型參數、歸零模型梯度。
??而在學習率調度過程中，由于我們需要動態調整學習率，而學習率又是通過傳入優化器進而影響模型訓練的，因此在利用PyTorch進行學習率調度的時候，核心需要考慮的問題是如何讓優化器內的學習率隨著迭代次數增加而不斷變化。
??為做到這一點，首先我們需要補充關于優化器狀態字典內容。

1.1 優化器相關參數介紹

# 設置隨機數種子
torch.manual_seed(420)  
# 創建最高項為2的多項式回歸數據集
features, labels = tensorGenReg(w=[2, -1, 3, 1, 2], bias=False, deg=2)
# 進行數據集切分與加載
train_loader, test_loader = split_loader(features, labels, batch_size=50)# 設置隨機數種子
torch.manual_seed(24)  
# 實例化模型  
tanh_model1 = net_class2(act_fun= torch.tanh, in_features=5, BN_model='pre')
# 創建優化器
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.01)
# 查看優化器狀態
optimizer.state_dict()

在優化器創建完成之后，我們可以使用.state_dict()方法查看優化器狀態。該方法會返回一個包含優化器核心信息的字典，目前為止該字典包含兩個元素，第一個是優化器狀態（state），第二個是優化器相關參數簇（param_groups）。
（1）學習率 lr
其中，目前為止核心需要關注的是參數簇中的lr對象，該對象代表著下一次模型訓練的時候所帶入的學習率。當然，我們可以通過如下方法提取lr對應的value

optimizer.state_dict()['param_groups']
optimizer.state_dict()['param_groups'][0]
optimizer.state_dict()['param_groups'][0]['lr']

參數簇中其他參數包括動量系數、特征權重、是否采用牛頓法及待訓練參數索引。

（2）模型參數索引
另外，params表示訓練參數個數（其中一個矩陣算作一個參數），可以通過如下方式進行簡單驗證。

list(tanh_model1.parameters())
# 驗證帶訓練參數個數
len(list(tanh_model1.parameters()))

1.2 模型的本地保存與讀取方法

??借助state_dict()方法，可以實現模型或優化器的本地保存于讀取。此處以模型為例，優化器的本地保存相關操作類似。模型的訓練和保存，本質上都是針對模型的參數。而模型的state_dict()則包含了模型當前全部的參數信息。因此，保存了模型的state_dict()就相當于是保存了模型。

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model1 = net_class2(act_fun= torch.tanh, in_features=5, BN_model='pre')# 通過`torch.save`將模型參數保存至本地
# 第一個參數：需要保存的模型參數，第二個參數：保存到本地的文件路徑及名稱
tanh_model1.state_dict()
torch.save(tanh_model1.state_dict(), 'tanh1.pt')

??進行模型訓練，即模型參數調整。通過損失函數和反向傳播機制進行梯度求解，利用優化器根據梯度值去更新各線性層參數。

criterion = nn.MSELoss()
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.05)
for X, y in train_loader:yhat = tanh_model1.forward(X)loss = criterion(yhat, y)optimizer.zero_grad()loss.backward()optimizer.step()
# 訓練完一輪之后，查看模型狀態
tanh_model1.state_dict()

我們發現模型的參數已經發生了變化。此時，如果我們想還原tanh_model1中原始參數，我們只能考慮通過使用load_state_dict方法，將本次保存的原模型參數替換當前的tanh_model1中參數，具體方法如下：

# 讀取（還原）保存的模型參數結果，使用load_state_dict方法和`torch.load`函數
tanh_model1.load_state_dict(torch.load('tanh1.pt'))
tanh_model1.state_dict()

除了模型可以按照上述方法保存外，優化器也可以類似進行本地存儲。

接下來，我們通過調用optim模塊中lr_scheduler相關函數，來實現優化器中學習率的動態調整。

二、LambdaLR基本使用方法

??讓優化器動態調整學習率的類，也被我們稱為學習率調度器類，該類實例化的對象也被稱為學習率調度器。在所有的學習率調度器中，LambdaLR類是實現學習率調度最簡單靈活、同時也是最通用的一種方法。
（1）lambda匿名函數
??要使用LambdaLR來完成學習率調度，首先需要準備一個lambda匿名函數，例如：

lr_lambda = lambda epoch: 0.5 ** epoch
# 第一輪迭代時
lr_lambda(0)
# 第二輪迭代時
lr_lambda(1)

此處我們通過lambda創建了一個匿名函數。該函數需要輸入一個參數，一般來說我們會將該參數視作模型迭代次數。當然上述匿名函數是個非常簡單的匿名函數，輸出結果就是0.5的epoch次方。

此處需要注意，一般來說epoch取值從0開始，并且用于學習率調度的匿名函數參數取值為0時，輸出結果不能為0。

（2）LambdaLR使用
??在準備好一個匿名函數之后，接下來我們需要實例化一個LambdaLR學習率調度器。

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model1 = net_class2(act_fun= torch.tanh, in_features=5, BN_model='pre')
# 創建優化器
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.05)
# 查看優化器信息
optimizer.state_dict()# 創建學習率調度器
# 參數包括與之關聯的優化器和一個lambda函數
lr_lambda = lambda epoch: 0.5 ** epoch
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda)
# 查看優化器信息
optimizer.state_dict()

??此時優化器的參數簇中多了 initial_lr元素，代表初始學習率，在實例化優化器時輸入的學習率。而優化器中的lr，則仍然表示下一次迭代時的學習率。對于LambdaLR學習調度來說，優化器中的lr伴隨模型迭代相應調整的方法如下：
$$lr=lr\_lambda(epoch)?initial\_lr$$
??并且，第一次實例化LambdaLR時epoch取值為0時，因此此時優化器的lr計算結果如下：$$l{r}_0=0.5^0?0.05=0.05$$
而在后續計算過程中，每當我們調用一次scheduler.step()，epoch數值就會+1。當一輪訓練完成時，我們可通過scheduler.step()來更新下一輪迭代時的學習率。

for X, y in train_loader:yhat = tanh_model1.forward(X)loss = criterion(yhat, y)optimizer.zero_grad()loss.backward()optimizer.step()
# 更新下一輪(epoch)迭代時的學習率
scheduler.step()
# 查看優化器信息
optimizer.state_dict()

需要注意，在上述模型訓練的代碼中，之所以將學習率調度器放在模型小批量梯度下降循環的外側，也是因為一般來說遍歷一次完整訓練集（一個epoch）才會對學習率進行一次更新，而不是每次計算完一個小批數據就對模型學習率進行更新。

而此時lr的取值0.025，則是由lr_lambda當epoch取值為1時的輸出結果和initial_lr相乘之后的結果。也就是$lr=0.5^1?0.05=0.025$。而如果把上述過程封裝為一個循環（也就是此前定義的fit函數），則下次模型訓練時學習率就調整為了0.025。至此，我們也就知道了scheduler.step()的真實作用——令匿名函數的自變量+1，然后令匿名函數的輸出結果與initial_lr相乘，并把計算結果傳給優化器，作為下一次優化器計算時的學習率。
??當然，我們也能簡單的重復optimizer.step()與scheduler.step()，即可一次次完成計算新學習率、并將新學習率傳輸給優化器的過程。

optimizer.zero_grad()
optimizer.step()
scheduler.step()        # lr 0.025 --> 0.0125lr_lambda = lambda epoch: 0.5 ** epoch
optimizer.state_dict()  # 優化器 lr 0.0125
scheduler.state_dict()  # 學習率調度器 lr 0.0125

不出意外，在第三次scheduler.step()時，匿名函數輸出結果為$0.5^2$，再與initial_lr相乘之后結果為0.0125。此處需要注意，PyTorch中要求先進行優化器的step，再進行學習率調度的step，此處需要注意先后順序。 另外，上述過程之所以提前將優化器內保存的模型參數清零，也是為了防止上述實驗過程最終導致模型參數被修改（梯度為0時模型無法修改參數）當然，每一輪epoch都讓模型學習率衰減50%其實是非常激進的。我們可以通過繪制圖像觀察學習率衰減情況。

# 創建優化器
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.05)
# 創建學習率調度器
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda)
optimizer.state_dict()['param_groups'][0]['lr']
lr_l = [0.05]
for i in range(10):optimizer.step()scheduler.step()lr = optimizer.state_dict()['param_groups'][0]['lr']lr_l.append(lr)
plt.plot(lr_l)
plt.xlabel('epoch')
plt.ylabel('Learning rate')

接下來，我們放緩學習率衰減速率，進行學習率調度建模實驗。

三、LambdaLR學習率調度實驗

3.1 前期準備與匿名函數定義

??在實驗開始前，我們需要將之前定義的fit_rec函數再次進行改寫，新函數需要包含學習率調度相關方法。

def fit_rec_sc(net, criterion, optimizer, train_data,test_data,scheduler,epochs = 3, cla = False, eva = mse_cal):"""加入學習率調度后的模型訓練函數（記錄每一次遍歷后模型評估指標）:param net：待訓練的模型 :param criterion: 損失函數:param optimizer：優化算法:param train_data：訓練數據:param test_data: 測試數據 :param scheduler: 學習率調度器:param epochs: 遍歷數據次數:param cla: 是否是分類問題:param eva: 模型評估方法:return：模型評估結果"""train_l = []test_l = []for epoch  in range(epochs):net.train()for X, y in train_data:if cla == True:y = y.flatten().long()          # 如果是分類問題，需要對y進行整數轉化yhat = net.forward(X)loss = criterion(yhat, y)optimizer.zero_grad()loss.backward()optimizer.step()scheduler.step()net.eval()train_l.append(eva(train_data, net).detach())test_l.append(eva(test_data, net).detach())return train_l, test_l

同樣，該函數需要寫入torchLearning.py文件中。接下來，我們定義一個衰減速度更加緩慢的學習率調度器。

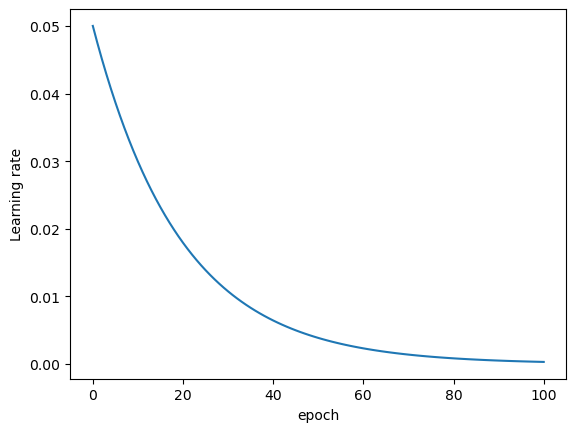
lr_lambda = lambda epoch: 0.95 ** epoch   # 相當于每迭代一輪學習率衰減5%

torch.manual_seed(24)  
# 創建優化器
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.05)
# 創建學習率調度器
lr_lambda = lambda epoch: 0.95 ** epoch  # 相當于每迭代一輪學習率衰減5%
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda)lr_l = [0.05]
for i in range(100):optimizer.step()scheduler.step()lr = optimizer.state_dict()['param_groups'][0]['lr']lr_l.append(lr)
plt.plot(lr_l)
plt.xlabel('epoch')
plt.ylabel('Learning rate')

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model1 = net_class2(act_fun=torch.tanh, in_features=5, BN_model='pre')
# 創建優化器
optimizer = torch.optim.SGD(tanh_model1.parameters(), lr=0.05)
# 創建學習率調度器
lr_lambda = lambda epoch: 0.95 ** epoch   # 相當于每迭代一輪學習率衰減5%
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda)
### 3.模型訓練與結果比較
# 進行模型訓練
train_l, test_l = fit_rec_sc(net = tanh_model1, criterion = nn.MSELoss(), optimizer = optimizer, train_data = train_loader,test_data = test_loader,scheduler = scheduler,epochs = 60, cla = False, eva = mse_cal)
plt.plot(train_l, label='train_mse')
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)

# 簡單驗證學習率最終調整結果。
optimizer.state_dict()
lr_lambda(60) * 0.05

當然，我們也可以繼續進行實驗，對比恒定學習率時計算結果

• 對比恒定學習率為0.03時模型訓練結果

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model1 = net_class2(act_fun= torch.tanh, in_features=5, BN_model='pre')
train_l3, test_l3 = fit_rec(net = tanh_model1, criterion = nn.MSELoss(), optimizer = optim.SGD(tanh_model1.parameters(), lr = 0.03), train_data = train_loader,test_data = test_loader,epochs = 60, cla = False, eva = mse_cal)
plt.plot(train_l, label='train_l')
plt.plot(train_l3, label='train_l3')
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)

我們發現，相比恒定學習為0.03的模型，加入學習率調度策略的模型（藍色線條），模型收斂效果更好、迭代更加平穩，且收斂速度較快。

• 對比恒定學習率為0.01時模型訓練結果

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model1 = net_class2(act_fun= torch.tanh, in_features=5, BN_model='pre')
train_l1, test_l1 = fit_rec(net = tanh_model1, criterion = nn.MSELoss(), optimizer = optim.SGD(tanh_model1.parameters(), lr = 0.01), train_data = train_loader,test_data = test_loader,epochs = 60, cla = False, eva = mse_cal)plt.plot(train_l, label='train_l')		# lr 0.05 學習率調節器，迭代優化
plt.plot(train_l3, label='train_l3')  	# lr 0.03
plt.plot(train_l1, label='train_l1')	# lr 0.01
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)

我們發現，相比恒定學習率為0.01的模型，擁有學習率調度的模型結果更優秀。

• 對比Lesson 15.1節中學習率調度模型

# 設置隨機數種子
torch.manual_seed(24)  # 實例化模型  
tanh_model = net_class2(act_fun=torch.tanh, in_features=5, BN_model='pre')
# 創建用于保存記錄結果的空列表容器
train_mse = []
test_mse = []# 創建可以捕捉手動輸入數據的模型訓練流程
while input("Do you want to continue the iteration? [y/n]") == "y":    # 詢問是否繼續迭代epochs = int(input("Number of epochs:"))                           # 下一輪迭代遍歷幾次數據lr = float(input("Update learning rate："))                        # 設置下一輪迭代的學習率train_l0, test_l0 = fit_rec(net = tanh_model, criterion = nn.MSELoss(), optimizer = optim.SGD(tanh_model.parameters(), lr = lr), train_data = train_loader,test_data = test_loader,epochs = epochs, cla = False, eva = mse_cal)train_mse.extend(train_l0)test_mse.extend(test_l0)
plt.plot(train_l, label='train_l')			# 60 0.05迭代優化
plt.plot(train_mse, label='train_mse')		# 30 0.03, 30 0.01
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)

很明顯，由于上一節的模型是0.03學習率模型和0.01學習率模型簡單疊加結果，在恒定學習率模型效果均不如本節模型的情況下，上一節課中的模型學習率調度策略也無法有更好的表現。

??但是，令人驚訝的是，在訓練了60輪之后，LambdaLR模型最終學習率在0.002附近，相比上述0.01學習率模型而言學習率更小。但從上述的實驗中我們發現，恒定學習率時從恒定0.03到恒定0.01的過程，模型準確率已經發生了明顯的下降，但在如果是采用動態調整學習率的策略，則可以在一個最終更小的學習率取值的情況下取得一個更好的模型結果。

??這其實說明損失函數在超平面空間的圖像比一般的想象要復雜的多，很多時候并不是越靠近全域最小值點附近的通道就越窄，會導致迭代過程落入局部最小值陷阱的學習率大小取值也只是絕對概念。正是由于損失函數的復雜性，才導致很多時候我們認為神經網絡的內部訓練是個“黑箱”，才進一步導致神經網絡的模型訓練往往以模型結果為最終依據，這也是神經網絡優化算法會誕生諸多基本原理層面比較扎實，但卻找不到具體能夠證明優化效果的理論依據的方法。
??不過，針對此類方法，和此前介紹的Batch Normalization一樣，盡管理論層面無法具體整體優化效果，但對于使用者來說仍然需要在了解其底層原理基礎上積累使用經驗或者調參經驗。因此在后續的課程中，我們將在繼續介紹其他學習率優化方法的同時，通過大量的實踐來快速積累使用經驗，并且在更多事實的基礎上找到解釋和理解的角度。