LLM 論文精讀（三）Demystifying Long Chain-of-Thought Reasoning in LLMs

這是一篇2025年發表在arxiv中的LLM領域論文，主要描述了長思維鏈 Long Chain-of-Thought 對LLM的影響，以及其可能的生成機制。通過大量的消融實驗證明了以下幾點：

與shot CoT 相比，long CoT 的 SFT 可以擴展到更高的性能上限；
較長 CoT 的 SFT 相比于短的 CoT 而言進一步改進 RL 變得更容易；
SFT 初始化至關重要：高質量、涌現的long CoT 模式能夠顯著提高泛化能力和強化學習的收益；
CoT 的長度并不總是以穩定的方式增加；
構建獎勵函數可以用來穩定和控制CoT長度，同時提高準確率；
余弦獎勵可以進行調整，以激勵各種長度擴展行為；
模型可能需要更多訓練樣本來學習到如何利用更大的上下文窗口大小；
長度獎勵將通過足夠的計算進行破解，但可以使用重復懲罰來緩解；
不同類型的獎勵和懲罰具有不同的最優折扣因子；
向 SFT 添加噪聲但多樣化的數據，可在不同任務之間實現均衡的性能；

作者在文章最后提到了LLM的“推理”能力的一個可能來源是：預訓練數據中包含了人類論壇中問答對話的內容，所以作者認為基于海量互聯網數據預訓練得到的模型仍然有未被人類關注到的其他能力。

寫在最前面

為了方便你的閱讀，以下幾點的注意事項請務必了解：

該系列文章每個字都是我理解后自行翻譯并寫上去的，可能會存在筆誤與理解錯誤，如果發現了希望讀者能夠在評論區指正，我會在第一時間修正錯誤。
閱讀這個系列需要你有基本的 RL、DL 相關基礎知識，有時候我會直接使用英文名詞，因為這些詞匯實在不容易找到符合語境的翻譯。
原文可能因為版面限制存在圖像表格與段落不同步的問題，為了更方便閱讀，我會在博文中重新對圖像表格進行排版，并做到引用圖表的文字下方就能看到被引用的圖表。因此可能會出現一張圖片在博客中多處位置重復出現的情況。
對于原文中的圖像，我會在必要時對圖像描述進行翻譯并附上我自己的理解，但如果圖像描述不值得翻譯我也不會強行寫上去。

Basic Information

論文標題：Demystifying Long Chain-of-Thought Reasoning in LLMs
原文鏈接: https://arxiv.org/abs/2502.03373
發表時間：2025年02月05日
發表平臺：arxiv
預印版本號：[v1] Wed, 5 Feb 2025 17:13:32 UTC (771 KB)
作者團隊：Edward Yeo, Yuxuan Tong, Morry Niu, Graham Neubig, Xiang Yue
院校機構：
- Tsinghua University;
- Carnegie Mellon University;
項目鏈接: 【暫無】
GitHub倉庫: https://github.com/eddycmu/demystify-long-cot

Abstract

擴展推理計算可增強大型語言模型 (LLM) 的推理能力，而長思維鏈 (Long CoT) 可實現回溯和糾錯等策略。強化學習 (RL) 已成為開發這些能力的重要方法，但Long CoT 出現的條件仍不清楚，并且 RL 訓練需要謹慎的設計選擇。本文中作者系統地研究了Long CoT 推理機制，確定了模型能夠生成Long CoT 軌跡的關鍵因素。通過大量的監督微調 (SFT) 和 RL 實驗，得出了四個主要發現：（1）雖然 SFT 并非絕對必要，但可以簡化訓練并提高效率；（2）推理能力往往會隨著訓練數據的增加而涌現，但發展方向并不能得到保證，因此獎勵策略對于穩定 CoT 長度增長至關重要；（3）擴展可驗證的獎勵信號對于 RL 至關重要，利用帶有噪聲的網絡提取解決方案并結合過濾機制，展現出強大的潛力，尤其適用于 STEM 推理等分布外 (OOD) 任務；(4)諸如糾錯之類的核心能力本身就存在于基礎模型中，但要通過強化學習有效地激勵這些技能用于復雜任務需要大量計算，而衡量其有效性則需要一種細致入微的方法。這些見解為優化訓練策略以增強 LLM 中的Long CoT 推理提供了實用指導。代碼：https://github.com/eddycmu/demystify-long-cot。

1. Introduction

大型語言模型 (LLM) 在數學和編程等領域展現出卓越的推理能力。實現 LLM 推理能力的一項關鍵技術是思路鏈 (CoT) 提示，它引導模型在得出最終答案之前生成中間推理步驟。

但即使有了CoT，LLM仍然難以應對高度復雜的推理任務，例如數學競賽、博士級科學質量保證、軟件工程。近期 OpenAI 的o1模型在這些任務中取得了重大突破。這些模型的一個關鍵特征是它們能夠利用較長的CoT來擴展推理計算，其中包括識別和糾正錯誤、分解困難步驟、迭代替代方法等策略，從而實現更長、更結構化的推理過程。

有多項研究嘗試通過訓練 LLM 生成Long CoT 來復制 o1 模型的性能，這些方法大多依賴于可驗證的獎勵，例如基于真實答案的準確率，這有助于避免在大規模強化學習 (RL) 中出現 reward hacking。然而，對于模型如何學習和生成Long CoT 的全面理解仍然有限。本文作者系統地研究了Long CoT 生成的潛在機制：

Supervised fine-tuning (SFT) for long CoTs：實現Long CoT 推理的最直接方法是SFT，分析了其擴展行為及其對強化學習的影響，發現Long CoT SFT 能夠使模型達到更高的性能，并且比shot CoT 更容易的強化學習的優化；
Challenges in RL-driven CoT scaling：觀察到強化學習并非總能穩定延長 CoT 的長度和復雜度。為了解決這個問題，作者引入了 cosine length-scaling 獎勵和重復懲罰，在穩定增長 CoT 的前提下，又能鼓勵諸如分支和回溯等新興推理行為；
Scaling up verifiable signals for long CoT RL：可驗證的獎勵信號對于穩定Long CoT 強化學習至關重要。然而由于高質量、可驗證數據的有限，擴大其規模仍然具有挑戰性。為了解決這個問題，作者探索了使用從網絡獲取的包含噪聲的數據。雖然這些次優監督信號會帶來不確定性，但通過在SFT中適當結合并在強化學習中進行過濾，表現出了良好的前景，尤其是在out-of-domain的推理場景中，例如STEM問題解決；
Origins of Long CoT Abilities and RL Challenges：分支和錯誤驗證等核心技能本身就存在于基礎模型中，但有效的強化學習驅動的激勵機制需要精心設計。作者研究了強化學習對long CoT 生成的影響，追蹤了預訓練數據中的推理模式，并討論了衡量這些模式出現的細微差別；

2. Problem Formulation

本節定義符號，然后概述了用于引出 Long CoT 的 SFT 和 RL 方法。

在這里插入圖片描述

2.1 Notation

令 $x$ 為query； $y$ 為output sequence，考慮一個以 $\theta$ 為參數的 LLM，定義了輸出token 的條件分布： $\pi_{\theta}(y_{t}|x,y_{1:t-1})$ 。

將輸出中構成CoT的tokens記為 $CoT(y)\subseteq y$ ，CoT 通常是一個推理軌跡或解釋序列。最終答案可以是一組獨立的token，也可以僅僅是 $y$ 的最后一段。

使用術語長 long CoT 來描述推理標記的擴展序列，表現為比平常更長的token長度，而且還表現出更復雜的行為，例如：

Branching and Backtracking：模型系統地探索多條路徑（branching），如果某條路徑被證明是錯誤的，則向后回溯（backtracking）；
Error Validation and Correction：模型檢測中間步驟中的不一致或錯誤，并采取糾正措施以恢復連貫性和準確性；

2.2 Supervised Fine-Tuning (SFT)

一種常見的做法是在數據集 $D_{SFT}=\{(x_{i},y_{i})\}^{N}_{i=1}$ 上通過 SFT 初始化策略 $\pi_{\theta}$ ，其中 $y_{i}$ 可以是常規或long CoT 推理tokens。

2.3 Reinforcement Learning (RL)

在可選的 SFT 初始化之后，使用強化學習進一步優化長 CoT 的生成。

Reward Function

定義一個標量獎勵 $r_{t}$ 旨在鼓勵正確且可驗證的推理。僅考慮基于最終答案結果的獎勵，而不考慮中間步驟的基于過程的獎勵，用 $r_{answer}(y)$ 來表示最終解決方案的正確性。

Policy Update

在實驗中采用近端策略優化 PPO 作為默認策略優化方法。在 7.3 小節中簡要討論了強化學習方法。采用基于規則的驗證器作為獎勵函數，該驗證器直接將預測答案與真實答案進行比較。由此產生的更新會推動策略生成能夠產生更高獎勵的 token。

2.4 Training Setup

采用 Llama-3.1-8B 和 Qwen2.5-7B-Math 作為基礎模型，它們分別是具有代表性的通用模型和數學專用模型。對于 SFT 和 RL，默認使用 MATH 的 7,500 個訓練樣本提示集，并使用該提示集提供可驗證的 ground truth 答案。對于 SFT，當 ground truth 答案可用時，通過拒絕抽樣來合成響應。具體而言，首先對每個prompt抽取固定數量 $N$ 的候選答案，然后進行篩選，只保留最終答案與相應真實答案一致的答案。作者在類似 WebInstruct的數據上進行了實驗，雖然這些數據更加多樣化，但沒有像 ground truth 那樣的監督信號。使用 OpenRLHF 框架來訓練模型。

2.5 Evaluation Setup

重點關注四個具有代表性的推理基準：MATH-500、AIME 2024、TheoremQA、MMLU-Pro-1k。鑒于訓練數據主要來自數學領域，這些基準為in-domain（MATH-500 測試集）和out-of-domain（AIME 2024、TheoremQA、MMLU-Pro-1k）的評估提供了一個全面的框架。默認情況下，使用溫度 $t = 0.7$ 、 $t o p ? p = 0.95$ 和最大輸出長度 16,384 個tokens來生成模型。有關評估設置的更多詳細信息，請參閱附錄 E.1。

3. Impact of SFT on Long CoT

本節比較 SFT 和 RL 初始化背景下的長 CoT 數據和短 CoT 數據。

3.1 SFT Scaling

比較long CoT 與shot CoT 的第一步是為模型配備相應行為。最直接的方法是基于 CoT 數據對基礎模型進行微調。由于shot CoT 很常見，因此通過從現有模型中剔除樣本來整理shot CoT 的 SFT 數據相對簡單。然而，如何獲取高質量的long CoT 數據仍然是一個懸而未決的問題。

Setup

對于long CoT，從 QwQ-32B-Preview 中提取數據（3.3 中討論其他long CoT 數據構建方法）；對于shot CoT，從 Qwen2.5-Math-72B-Instruct 中提取數據，這是一個在數學推理中功能強大的shot CoT 模型。具體而言，通過對每個prompt采樣 $N$ 個候選答案，然后篩選出正確答案來執行拒絕抽樣；對于long CoT，使用 $\in {32, 64, 128, 192, 256}$ ，而對于shot CoT，使用 $\in {32, 64, 128, 256}$ ，為了提高效率跳過一個 $N$ 。在每種情況下，SFT tokens的數量都與 $N$ 成正比，基礎模型為 Llama-3.1-8B。有關 SFT 設置的更多詳細信息，請參閱附錄 E.3。

【Note】這里初學者可能會提出疑問：如果標準答案中有一些主觀描述的部分，模型輸出中也有一些主觀描述的內容，那么應該如何選擇出正確的那條輸出？通常情況下有以下四個方法：

引入多維評分機制
- 置信度評分：要求模型在給出答案的同時輸出自我評估置信度，選取置信度最高的作為答案；
- 多樣性評分：剔除答案之間的語意相似性，減少高度重復的冗余答案；
- 主觀描述合理性評分：使用情感分析篩選出語意流暢的答案；
使用輔助模型驗證
- 提取特征并重評分：用另外一個判別模型來對答案進行特征提取與打分；
- 交叉驗證：用多個大規模預訓練模型對答案進行驗證（Llama4、Qwen、GPT-4），如果一個答案在多個模型上都得到了高分，那么就用這個答案；
Human-in-the-loop：人工評估哪個答案最符合人類水平，但這種方式存在較高的不確定性；
反向驗證：根據答案讓模型反向生成問題，然后再與原始問題進行對比，找到最接近的那條；

Result

Fig.1 中的虛線表明，隨著 SFT tokens數量的增加，long CoT SFT 持續提升模型準確率，而短 CoT SFT 則在較低的準確率水平上提前飽和。例如，在 MATH-500 上，long CoT SFT 的準確率超過 70%，即使在 35 億個tokens時也未達到穩定水平。相比之下，shot CoT SFT 的準確率收斂到 55% 以下，SFT tokens數量從約 2.5 億增加到 15 億，僅帶來約 3% 的絕對提升。

在這里插入圖片描述

3.2 SFT Initialization for RL

先前的研究表明 RL 具有比 SFT 更高的上限，作者將long CoT 和shot CoT 作為 RL 的不同 SFT 初始化方法進行比較。

Setup

使用3.1中的SFT checkpoint 初始化強化學習并訓練四個周期，每個prompt采樣四個響應。用PPO和MATH數據集中基于規則的驗證器，并將其訓練樣本作為我們的強化學習提示集。使用余弦長度縮放獎勵和重復懲罰，這將在章節4中詳細說明。關于的強化學習設置和超參數的更多詳細信息，可分別參見附錄E.4和E.5.1。

Result

Fig.1 中實線和虛線之間的間隙表明，用long CoT SFT 初始化的模型通常可以通過 RL 獲得更顯著的提升，而用shot CoT SFT 初始化的模型則幾乎無法從 RL 中獲益。例如，在 MATH-500 上，RL 可以將long CoT SFT 模型的絕對精度提升 3% 以上，而shot CoT SFT 模型在 RL 前后的準確率幾乎相同。

在這里插入圖片描述

3.3 Sources of Long CoT SFT Data

為了獲取long CoT 內容，作者比較了兩種方法：

通過提示shot CoT 模型生成原始動作并按順序組合它們來構建long CoT 軌跡；
從表現出long CoT 模式的現有模型中提取long CoT 軌跡；

Setup

為了構建較長的CoT軌跡，作者開發了一個行動提示框架 E.8，該框架定義了以下基本行為：clarify、decompose、solution step、reflection、answer。采用多步驟提示和shot CoT模型（例如Qwen2.5-72B-Instruct）來對這些行動進行排序，而更強大的模型o1-mini-0912則生成包含自我修正的反思步驟。為了提煉較長的CoT軌跡，使用QwQ-32-Preview作為教師模型。在這兩種方法中，都采用MATH訓練集作為提示集并使用了拒絕抽樣。為了確保公平，用相同的基礎模型Llama-3.1-8B，維護約20萬個SFT樣本，并使用與3.2中相同的強化學習設置。

Result

Table.1 顯示，從涌現的long CoT 模式提煉出的模型比構造模式具有更好的泛化能力，并且可以通過 RL 進一步顯著提升，而用構造模式訓練的模型則不能。用涌現的long CoT 模式訓練的模型在 OOD 基準 AIME 2024 和 MMLU-Pro-1k 上實現了顯著更高的準確率，相對提高了 15-50%。此外，在 OOD 基準 TheoremQA 上，long CoT SFT 模型上的 RL 將其準確率顯著提高了約 20%，而shot CoT 模型的性能沒有變化。這也是為什么作者大部分實驗都是基于提煉出的long CoT 軌跡進行的。

在這里插入圖片描述

4. Impact of Reward Design on Long CoT

本節研究獎勵函數設計，重點關注其對 CoT 長度和模型性能的影響。

4.1 CoT Length Stability

最近關于long CoT 的研究表明，隨著思考時間的增加，模型在推理任務中的表現會自然提升。作者的實驗也證實，基于從 QwQ-32B-Preview 中提煉出的long CoT 進行微調的模型，在強化學習訓練中往往會延長 CoT 的長度，盡管有時并不穩定。Kimi Team 和 Hou 也指出了這種不穩定性，并已使用基于長度和重復懲罰的技術來穩定訓練。

Setup

使用兩個不同的模型，它們基于從 QwQ-32B-Preview 中提取的long CoT 數據進行微調，使用 MATH 訓練拆分，上下文窗口大小為 16K。這兩個模型分別是 Llama3.1-8B 和 Qwen2.5-Math-7B。用一個基于規則的驗證器，并對正確答案設置了簡單的 1 獎勵，作者將其稱為Classic Reward。更多詳細信息請參見附錄 E.5.2。

Results

兩個模型在訓練過程中都增加了上下文連接長度 (CoT)，最終達到了上下文窗口的極限。由于上下文連接長度超過了允許的窗口大小，這導致訓練準確率下降。此外，不同的基礎模型表現出不同的縮放行為。如Fig.2 所示，性能較弱的 Llama-3.1-8B 模型的上下文連接長度波動更大。

在這里插入圖片描述

作者還發現，CoT 超出上下文窗口大小的速率在低于 1 的某個閾值時趨于平穩Fig.2。這表明超出限制開始對 CoT 長度分布施加顯著的下行壓力，并凸顯了上下文窗口大小在隱式長度懲罰中的作用。即使沒有明確的超長懲罰，軌跡也可能因為獎勵或優勢歸一化而受到懲罰，而獎勵或優勢歸一化在強化學習框架中都是標準做法。

在這里插入圖片描述

4.2 Activate Scaling of CoT Length

獎勵塑造可以用來穩定涌現的長度縮放。作者設計了一個獎勵函數，將 CoT 長度作為額外輸入，并遵循一些排序約束：

正確的 CoT 比錯誤的 CoT 獲得更高的獎勵；
較短的正確 CoT 比較長的正確 CoT 獲得更高的獎勵，這激勵模型有效地使用推理計算；
較短的錯誤 CoT 應該比較長的錯誤 CoT 受到更高的懲罰，這鼓勵模型在不太可能得到正確答案的情況下延長其思考時間。

使用分段余弦函數易于調整且平滑，將此獎勵函數稱為余弦獎勵Fig.3，僅在 CoT 結束時根據答案的正確性授予一次。CosFn 的公式可在附錄中的Equation.1中找到。

$R(C,L_{gen})= \begin{cases} CosFn(L_{gen},L_{max},r^{c}_{0},r^{c}_{L}), & \text{if } C=1,\\ CosFn(L_{gen},L_{max},r^{w}_{0},r^{w}_{L}), & \text{if } C=0,\\ r_{e}, & \text{if } L_{gen}=L_{max} \end{cases}$

Hyperparameters:

$\begin{align} r^{c}_{0}/r^{w}_{0}: & \text{Reward (correct/wrong) for } L_{gen}=0,\nonumber \\ r^{c}_{L}/r^{w}_{L}: & \text{Reward (correct/wrong) for } L_{gen}=L_{max},\nonumber \\ r_{e}: &\text{Exceed length penalty} \nonumber \end{align}$

Inputs:

$\begin{align} C:& \text{Correctness (0 or 1)}\nonumber \\ L_{gen}: &\text{Generation length} \nonumber \end{align}$

在這里插入圖片描述

Setup

用經典獎勵和余弦獎勵進行了實驗，使用 Llama3.1-8B 進行微調，該微調基于從 QwQ-32B-Preview 中提取的long CoT 數據，并使用 MATH 訓練集拆分作為起點。更多詳細信息，請參閱附錄 E.5.3。

Result

余弦獎勵顯著穩定了強化學習下模型的長度縮放行為，從而穩定了訓練準確率并提升了強化學習效率Fig.4，同時還觀察到模型在下游任務上的表現有所提升Fig.5。

在這里插入圖片描述

4.3 Cosine Reward Hyperparameters

調整余弦獎勵超參數以不同方式塑造 CoT 長度。

Setup

用相同的模型進行強化學習實驗，該模型基于從 QwQ-32B-Preview 中提煉出的long CoT 進行微調，但余弦獎勵函數使用了不同的超參數，作者調整了正確和錯誤獎勵 $r^{c}_{0}$ 、 $r^{c}_{L}$ 、 $r^{w}_{0}$ 、 $r^{w}_{L}$ ，并觀察其對 CoT 長度的影響。更多詳情，請參閱附錄 E.5.4。

Result

從附錄中的Fig.9 中看到，如果正確答案的獎勵隨著 CoT 長度的增加而增加 $r^{c}_{0}<r^{c}_{L}$ ，CoT 長度就會爆炸式增長；正確獎勵相對于錯誤獎勵越低，CoT 長度就越長。作者將其解讀為一種訓練有素的風險規避機制，其中正確獎勵和錯誤獎勵的比例決定了模型對答案的置信度，才能使其在以答案終止 CoT 時獲得正的預期值。

在這里插入圖片描述

4.4 Context Window Size

更長的上下文會給模型更大的探索空間，隨著訓練樣本的增加，模型最終會學會利用更多的上下文窗口。這就引出了一個有趣的問題：是否需要更多的訓練樣本才能學會利用更大的上下文窗口？

Setup

使用相同的初始模型，并基于從 QwQ-32B-Preview 中提取的long CoT 數據進行微調，根據 MA??TH 訓練進行拆分，使用后者作為強化學習提示集。每次消融實驗都使用了余弦獎勵和重復懲罰，并使用不同的上下文窗口大小（4K、8K、16K）。更多詳情，請參閱附錄 E.5.5。

Result

上下文窗口大小為 8K 的模型表現優于 4K 的模型，這與預期一致。然而，觀察到 8K 的性能優于 16K 的性能。這三個實驗都使用了相同數量的訓練樣本Fig.6。作者認為這表明模型需要更多的訓練計算才能學會充分利用更長的上下文窗口大小。

在這里插入圖片描述

4.5 Length Reward Hacking

在獲得足夠的訓練數據后，該模型開始出現 reward hacking 跡象，即它通過重復而不是學習解決難題來增加其在難題上的分支時間 CoT 的長度，同時模型的分支頻率有所下降，這是通過計算樞紐關鍵詞 “alternatively” 在CoT中出現的次數來估算的Fig.10。

在這里插入圖片描述

通過使用一個簡單的 N-gram 重復懲罰（Algorithm 1）來緩解這個問題。該懲罰用于重復的 token，而非對整個CoT軌跡進行評估，在計算回報時降低重復懲罰也是有效的。關于重復發生位置的具體反饋，大概能讓模型更容易學會避免重復。

Setup

使用 Llama3.1-8B，該模型基于從 QwQ-32B-Preview 中提取的long CoT 數據進行了微調。兩次強化學習訓練，均使用了余弦獎勵，但分別使用了重復懲罰和未使用重復懲罰。更多詳細信息，請參閱附錄 E.5.6。

Result

重復懲罰導致更好的下游任務性能和更短的 CoT，這意味著推理計算的效率更高Fig.5。

在這里插入圖片描述

Observation

實驗揭示了重復懲罰、訓練準確率、余弦獎勵之間的關系。當訓練準確率較低時，余弦獎勵會對 CoT 長度施加更大的上行壓力，導致通過重復進行的獎勵黑客攻擊增加。這反過來又需要更強的重復懲罰。未來的工作可以進一步研究這些相互作用，并探索動態調整方法以實現更好的優化。

在這里插入圖片描述

4.6 Optimal Discount Factors

假設使用時間局部性（即較低的折扣因子）的重復懲罰會最有效，因為其能提供關于特定違規token的更強信號。然而作者發現，當余弦獎勵的折扣因子過低時，性能會下降。

為了對兩種獎勵類型進行最佳調整，作者修改了 PPO 中的 GAE 公式，使其能夠適應多種獎勵類型，每種獎勵類型都有各自的折扣因子 $\gamma:\hat{A}_{t}=\sum^{L}_{l=0}\sum^{M}_{m}\gamma^{l}_{m}r_{m,t+l}-V(s_{t})$ 。作者在這里設定 $\lambda = 1$ ，實驗證明該方案是可行的，雖然并未對此參數進行廣泛的測試。

Setup

使用相同的 Llama3.1-8B 模型，并在 QwQ-32B-Preview 提取的long CoT 數據上微調，開展了多次強化學習實驗。使用余弦獎勵和重復懲罰，但采用了不同的折扣因子組合。更多詳情，請參閱附錄 E.5.7。

Result

較低的折扣因子有效地強化了重復懲罰，而較高的折扣因子則增強了正確性獎勵和超長懲罰。較高的折扣因子使得模型能夠因在CoT中較早地選擇正確答案而獲得足夠的獎勵Fig.5。

觀察到一個相當有趣的現象：降低余弦獎勵的折扣因子會增加模型 CoT 中的分支頻率，使得模型很快放棄那些似乎不能立即得出正確答案的方法附錄 D Fig.11 。作者認為這種短期思維是由于在正確答案之前獲得獎勵的tokens數量相對較少，這意味著通往正確答案的前的tokens被低估了，從而降低了性能Fig.5。然而，作者認為這個定性結果可能引起研究界的興趣，因為它與延遲滿足等行為與生物大腦獲得的獎勵分配之間的關系相似。

在這里插入圖片描述

5. Scaling up Verifiable Reward

可驗證的獎勵信號（例如基于真實答案的獎勵信號）對于穩定推理任務的long CoT 強化學習至關重要。然而，由于用于推理任務訓練的高質量人工標注數據有限，因此很難擴展此類數據。為了解決這個問題，使用其他容易獲取但噪聲更大的數據，例如從網絡語料庫中提取的與推理相關的問答對。具體而言使用 WebInstruct 數據集進行實驗。為了提高效率，構建了 WebInstruct-462k 一個通過最小哈希 MinHash 生成的去重子集。

5.1 SFT with Noisy Verifiable Data

研究如何將這種多樣化的數據添加到 SFT 中，盡管監督數據的可靠性較低，但多樣化的數據可能有助于強化學習期間模型的探索。

Setup

測試了三種配置，分別調整了不含監督數據的數據比例：0%、100%、50%，從 QwQ-32B-Preview 中提取數據進行long CoT SFT。對于含有監督信號MATH 的數據，使用真實答案進行拒絕采樣；對于來自 WebInstruct 的數據，雖然沒有完全可靠的監督信號，但規模更大，從教師模型中對每個提示采樣一個答案且不進行過濾。對于此處的強化學習，采用與 3.2 相同的設置，使用 MATH 訓練集。

Result

Table.2 顯示，結合次優監督數據可提升平均性能。將 WebInstruct 數據添加到 long CoT SFT 中，與單獨使用 MATH 相比，MMLU-Pro-1k 上的絕對準確率提升了 510%；混合使用 MATH 和 WebInstruct 數據可實現跨基準測試的最佳平均準確率。

在這里插入圖片描述

5.2 Scaling up RL with Noisy Verifiable Data

比較從有噪聲的可驗證數據中獲取獎勵的兩種??主要方法：

提取簡短形式的答案并使用基于規則的驗證器；
使用能夠處理自由形式響應的基于模型的驗證器；

這里的一個關鍵因素是問答對是否可以有簡短的答案。因此，比較數據集是否通過僅保留簡短答案的樣本進行過濾。

Setup

通過使用原始參考解決方案提示 Qwen2.5-Math-7B-Instruct 來實現基于模型的驗證器。為了提取簡短答案，首先提示 Llama-3.1-8B-Instruct 從原始響應中提取，然后使用 QwQ-32B-Preview 應用拒絕抽樣。具體而言從 WebInstruct-462k 中為每個prompt生成兩個結果，丟棄與提取的參考答案不一致的結果。此過程在 115k 個唯一提示中產生大約 189k 個響應。實驗表明，拒絕抽樣會丟棄許多prompt：

許多 WebInstruct 提示缺乏基于規則的驗證器可以有效處理的簡短答案；
某些提示甚至對于 QwQ-32B-Preview 來說也太難了。

對于 SFT 在過濾后的數據集上訓練 Llama-3.1-8B 作為強化學習 (RL) 的初始化。強化學習階段，未過濾設置中使用完整的 462k 個問題集，在過濾設置中使用 115k 個子集，并使用 30k 個問題集進行訓練，每個問題集有 4 個答案。關于基于模型的驗證器、答案提取和強化學習超參數的更多詳細信息，分別請參見附錄 E.5.8 & E.6 & E.7。

Result

Table.3 顯示，在相同數量的 RL 樣本下，帶有基于規則的驗證器的 RL 在經過篩選的包含簡短形式答案的提示集上在大多數基準測試中均取得了最佳性能。這可能表明，經過適當篩選后的基于規則的驗證器可以從嘈雜的可驗證數據中生成最高質量的獎勵信號。此外，與使用人工注釋的驗證數據 MATH 訓練的模型相比，利用嘈雜但多樣化的可驗證數據仍可顯著提升 OOD 基準測試的性能，在 TheoremQA 上的絕對增益高達 2.9%，在 MMLU-Pro-1k 上的絕對增益高達 6.8%。相比之下，將基于規則的驗證器應用于未篩選的數據會導致最差的性能。這可能是因為在自由形式答案上的訓練準確率較低，而基于模型的驗證器性能要好得多。

在這里插入圖片描述

6. Exploration on RL from the Base Model

DeepSeek-R1 已證明，通過在基礎模型上擴展強化學習能力，可以實現long CoT推理。近期研究嘗試通過運行相對較少次數的強化學習迭代來復制這一進展，以觀察長思維鏈行為（例如“頓悟時刻”，這是一個突現的頓悟時刻，能夠實現自我驗證和修正等關鍵功能）的出現。本節還將探討基于基礎模型的強化學習方法。

6.1 Nuances in Analysis Based on Emergent Behaviors

自我驗證行為有時會被模型的探索動作標記為突現行為或“頓悟時刻”，因為這類模式在短時間認知數據中并不常見。然而，有時自我驗證行為已經存在于基礎模型中，通過強化學習來強化這些行為需要滿足較為嚴格的條件，例如強大的基礎模型。

Setup

遵循 Zeng 等人的設置，使用基于規則的驗證器和 PPO 算法，對大約 8000 道數學 3-5 級題目訓練 Qwen2.5-Math-7B，同時也使用了作者自己基于規則的驗證器實現。在推理方面，溫度 $t = 0$ （貪婪解碼），初步實驗表明，對于直接通過 Qwen2.5-Math-7B 強化學習獲得的模型， $t = 0$ 通常表現顯著優于 $t > 0$ 。考慮到訓練上下文的長度為 4096 個 token，使用的最大輸出長度為 4096 個 token；對基礎模型使用了零樣本提示 (zero-shot prompting)，以避免在輸出模式中引入偏差。從先前研究中的long CoT案例中選取了五個具有代表性的關鍵詞：“wait”、“recheck”、“alternatively”、“retry”、“however”，并計算它們的出現頻率，以量化模型自我驗證的程度。關于強化學習超參數的更多細節，請參見附錄 E.5.9。

Result

Fig.7 顯示，基于 Qwen2.5-Math-7B 的強化學習有效地提升了準確率，但并未增加基礎模型輸出中存在的“重新檢查”模式的頻率，也未能有效地激勵其他反射模式，例如“重試”和“另外”。這表明，基于基礎模型的強化學習雖然顯著提升了性能，但并不一定會激勵反射模式。有時，基礎模型的輸出中也存在此類行為，而強化學習并不能顯著增強這些行為。因此可能需要更加謹慎地識別突發行為。

在這里插入圖片描述

6.2 Nuances in Analysis Based on Length Scaling

長度的增加被認為是模型有效探索的另一個重要特征。然而，有時長度的增加會伴隨 KL 散度的減小，這增加了長度可能受到 KL 懲罰的影響，只是回歸到基礎模型的較長輸出，而不是反映出長 CoT 能力的獲得。

Setup

設置與 6.1相同。除了輸出token長度之外，還計算了“coding rate”。由于Qwen2.5-Math-7B同時使用自然語言和編碼來解決數學問題，因此如果模型輸出包含“python”，則將模型輸出歸類為“coding”，這里的“coding”輸出實際上是自然語言輸出的一種特殊形式，其中的代碼不會被執行，代碼的輸出是由模型生成的。

Result

Fig.8 (1) 顯示，輸出 token 的長度在初始下降之后有所增加，但從未超過基礎模型的初始長度。

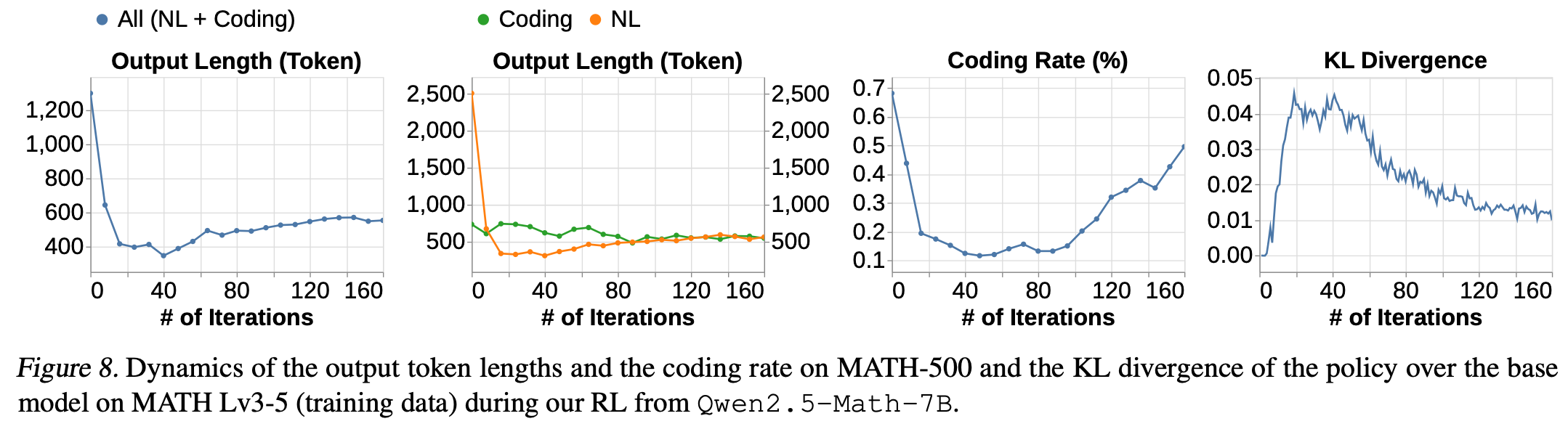
在這里插入圖片描述

Zeng 等人認為，初始下降可能是由于模型從生成較長的編碼輸出過渡到生成較短的自然語言輸出。然而Fig8 (2)表明，自然語言輸出實際上比編碼輸出更長，并且初始長度的下降在兩種類型的輸出中均有發生。此外Fig.8 (3)顯示編碼率隨后再次上升，這表明編碼和自然語言之間的區別可能不會對優化過程產生顯著影響。

作者懷疑后續的長度擴展并非源于模型的探索，因為當長度擴展時，策略相對于基礎模型的 KL 散度會下降，如Fig.8 (4) 所示。這可能表明 KL 懲罰影響了長度。如果是這樣，那么由于探索受到 KL 約束的限制，策略輸出長度幾乎不可能超過基礎模型的長度。

6.3 Potential Reasons Why Emergent Behavior is NOT Observed with Qwen2.5-Math-7B

對 Qwen2.5-Math-7B 強化學習模型進行了詳細分析，結果表明它未能完全復制 DeepSeek-R1 的訓練行為。作者確定了以下潛在原因：

基礎模型相對較小（7B 參數），在受到激勵時可能缺乏快速發展此類復雜能力的能力；
該模型可能在（持續的）預訓練和退火過程中過度暴露于類似 MATH 的短指令數據，導致過擬合并阻礙了long CoT 行為的發展。

6.4 Comparison between RL from the base Model and RL from Long CoT SFT

比較來自基礎模型的 RL 和來自long CoT SFT 的 RL 的性能，發現來自long CoT SFT 的 RL 通常表現更好。

Setup

使用基礎模型 Qwen2.5-Math-7B 進行比較。基礎模型的強化學習結果來自6.1 中訓練的模型。對于long CoT SFT 的強化學習，采用與 3.2 類似的設置。選擇 7.5k MATH 訓練集作為提示集，使用 QwQ-32B-Preview 對每個提示進行 32 個候選答案的拒絕采樣來整理 SFT 數據，并使用帶有重復懲罰的余弦長度縮放獎勵和基于規則的驗證器執行 PPO，每個提示采樣 8 個答案并訓練 8 個 epoch。為了使訓練前上下文長度僅為 4096 個 token 的 Qwen2.5-Math-7B 適應long CoT SFT 和強化學習，將其 RoPE $\theta$ 乘以 10 倍。由于long CoT SFT 的經典獎勵機制會崩潰，因此這里沒有對比其在強化學習中的應用結果。為了進行評估，采用 2.5 中long CoT SFT 強化學習的默認溫度采樣設置，以及 6.1 中基礎模型強化學習的貪婪解碼設置，以獲得最佳性能。關于蒸餾、SFT 超參數和強化學習超參數的更多詳細信息，可分別參見附錄 E.2、E.3 和 E.5.9。

Result

Table.4 顯示，在 Qwen2.5-Math-7B 上，基于long CoT SFT 模型初始化的強化學習性能顯著優于基于基礎模型的強化學習，并且比long CoT SFT 本身的性能有了進一步提升。具體而言，基于余弦獎勵的long CoT SFT 的強化學習平均比基于基礎模型的強化學習高出 8.7%，并且比 SFT 初始化的性能提升了 2.6%。值得注意的是，僅僅將 SFT 與從 QwQ-32B-Preview 中提煉出的long CoT 結合使用就已經獲得了強勁的性能。

6.5 Long CoT Patterns in Pre-training Data

根據6.1中的結果，假設一些激勵行為，例如模型重新訪問其解決方案，可能在預訓練過程中已經部分習得。為了驗證這一點，采用了兩種方法來評估此類數據是否已經存在于網絡上。

首先，使用生成式搜索引擎 Perplexity.ai 來識別明確包含問題解決步驟的網頁，這些步驟從多個角度解決問題，或在提供答案后進行驗證，使用的查詢和識別的示例見附錄 F.1。

其次，使用 GPT-4o 生成了一個表征“頓悟時刻”的短語列表（附錄 F.2.1），然后使用 MinHash 算法搜索 OpenWebMath，這是一個從 CommonCrawl中篩選出來的數據集，該數據集在預訓練中經常使用。發現在討論主題中存在大量匹配，其中多個用戶之間的對話與long CoT 相似，并且討論了多種方法以及回溯和錯誤糾正（附錄 F.2.2）。這提出了一個有趣的可能性，即long CoT 起源于人類對話，盡管討論是 OpenWebMath 中常見的數據來源。

基于這些觀察，作者假設強化學習主要引導模型將其在預訓練期間已內化的技能重新組合成新的行為，從而提高復雜問題解決任務的表現。鑒于本文的研究范圍廣泛，對這部分更深入研究留待未來研究。

7. Discussions and Futrue Work

在本文中，揭秘了LLM中long CoT推理的過程。本節概述了未來的潛在研究方向。

7.1 Scaling up Model Size

作者認為，模型大小是限制 6.1 小節中觀察到的行為出現的主要因素。Hyung Won Chung 等論文也表達了類似的觀點，認為較小的模型可能難以發展高級推理能力，而更傾向于依賴基于啟發式的模式識別。未來的研究可以使用更大的基礎模型來探究強化學習。

7.2 RL Infrastructure Is Still in Its Infancy

在嘗試擴大模型規模時，當擴展到 32B 時遇到了巨大的挑戰，最終確定所需的 GPU 數量太大而無法繼續。觀察到開源 RL 框架（例如 OpenRLHF）通常會協調針對不同訓練和推理工作負載進行優化的多個系統，這會導致內存中存儲模型參數的多個副本。此外，像 PPO 這樣的算法會同步且順序地在這些工作負載之間交替，進一步限制了效率。這些因素導致了硬件利用率低，這個問題在long CoT 場景中尤其嚴重，因為 CoT 長度的差異較大，導致推理過程中出現落后者。作者期待機器學習和系統研究的進步將有助于克服這些限制并加速long CoT 建模的進程。

7.3 Reinforce Is More Tricky to Tune than PPO

作者還探索了 REINFORCE++ 作為 PPO 的更快替代方案用于擴展數據。然而，發現它比 PPO 明顯不穩定，導致訓練準確率較低Fig.13。由于這種不穩定性可能是由于未調優的設置造成的（附錄 E.5.10），作者將其作為一項觀察結果提出但不會對其進行評價，希望對社區有所幫助。

7.4 Scaling up Verification

研究結果表明，將基于規則的驗證器與提示集過濾相結合非常有效，但設計此類規則并跨不同領域策劃提示集仍然需要大量勞動力。更重要的是，這種方法將人為設計的啟發式方法嵌入到強化學習環境中，反映了人類的思維習慣，而不是涌現式學習。正如《The Bitter Lesson》中所強調的那樣，手動編碼人類直覺往往是一種低效的長期策略，如何有效地擴展驗證信號是一個值得探討的話題。在設計強化學習環境的背景下，是否存在與預訓練相當的東西，作者期待未來對次優級監督信號以及強化學習驗證中自監督方法的潛力進行研究。

7.5 Latent Capabilities in Base Models

推理是基礎模型中一項最近才被解鎖的潛在能力。實驗表明，這種思維的一個可能來源是互聯網論壇上的人類對話。這引出了一個更廣泛的問題：還有哪些其他能力等待從預訓練數據中蘊含的海量人類知識和經驗中被挖掘出來？作者期待更詳細的分析，將模型行為追溯到其數據來源，從而可能產生新的見解，并有助于揭示基礎模型中隱藏的能力。