集成學習基礎應用實踐

集成學習簡介

學習目標：

1.知道集成學習是什么？

2.了解集成學習的分類

3.理解bagging集成的思想

4.理解boosting集成的思想

知道】集成學習是什么？

集成學習是機器學習中的一種思想，它通過多個模型的組合形成一個精度更高的模型，參與組合的模型成為弱學習器（基學習器）。訓練時，使用訓練集依次訓練出這些弱學習器，對未知的樣本進行預測時，使用這些弱學習器聯合進行預測。

傳統機器學習算法 (例如：決策樹，邏輯回歸等) 的目標都是尋找一個最優分類器盡可能的將訓練數據分開。集成學習 (Ensemble Learning) 算法的基本思想就是將多個分類器組合，從而實現一個預測效果更好的集成分類器。集成算法可以說從一方面驗證了中國的一句老話：三個臭皮匠，賽過諸葛亮

集成學習通過建立幾個模型來解決單一預測問題。它的工作原理是生成多個分類器/模型，各自獨立地學習和作出預測。這些預測最后結合成組合預測，因此優于任何一個單分類的做出預測。

【了解】集成學習分類

集成學習算法一般分為：bagging和boosting。

【理解】bagging集成

Baggging 框架通過有放回的抽樣產生不同的訓練集，從而訓練具有差異性的弱學習器，然后通過平權投票、多數表決的方式決定預測結果。

例子：

目標：把下面的圈和方塊進行分類

1) 采樣不同數據集

2)訓練分類器

3)平權投票，獲取最終結果

4)主要實現過程小結

【理解】boosting集成

Boosting 體現了提升思想，每一個訓練器重點關注前一個訓練器不足的地方進行訓練，通過加權投票的方式，得出預測結果。

Boosting是一組可將弱學習器升為強學習器算法。這類算法的工作機制類似：

1.先從初始訓練集訓練出一個基學習器

2.在根據基學習器的表現對訓練樣本分布進行調整，使得先前基學習器做錯的訓練樣本在后續得到最大的關注。

3.然后基于調整后的樣本分布來訓練下一個基學習器；

4.如此重復進行，直至基學習器數目達到實現指定的值T為止。

5.再將這T個基學習器進行加權結合得到集成學習器。

簡而言之：每新加入一個弱學習器，整體能力就會得到提升

Bagging 與 Boosting

區別一:數據方面

Bagging：有放回采樣
Boosting：全部數據集, 重點關注前一個弱學習器不足

區別二:投票方面

Bagging：平權投票
Boosting：加權投票

區別三:學習順序

Bagging的學習是并行的，每個學習器沒有依賴關系
Boosting學習是串行，學習有先后順序

隨機森林

學習目標：

1.理解隨機森林的構建方法

2.知道隨機森林的API

3.能夠使用隨機森林完成分類任務

【理解】算法思想

隨機森林是基于 Bagging 思想實現的一種集成學習算法，它采用決策樹模型作為每一個基學習器。其構造過程：

訓練：
1. 有放回的產生訓練樣本
2. 隨機挑選 n 個特征（n 小于總特征數量）
預測：平權投票，多數表決輸出預測結果

隨機森林的步驟

如上圖：

首先，對樣本數據進行有放回的抽樣，得到多個樣本集。具體來講就是每次從原來的N個訓練樣本中有放回地隨機抽取m個樣本(包括可能重復樣本)。

然后，從候選的特征中隨機抽取k個特征，作為當前節點下決策的備選特征，從這些特征中選擇最好地劃分訓練樣本的特征。用每個樣本集作為訓練樣本構造決策樹。單個決策樹在產生樣本集和確定特征后，使用CART算法計算，不剪枝。

最后，得到所需數目的決策樹后，隨機森林方法對這些樹的輸出進行投票，以得票最多的類作為隨機森林的決策。

說明：

（1）隨機森林的方法即對訓練樣本進行了采樣，又對特征進行了采樣，充分保證了所構建的每個樹之間的獨立性，使得投票結果更準確。

（2）隨機森林的隨機性體現在每棵樹的訓練樣本是隨機的，樹中每個節點的分裂屬性也是隨機選擇的。有了這2個隨機因素，即使每棵決策樹沒有進行剪枝，隨機森林也不會產生過擬合的現象。

隨機森林中有兩個可控制參數：

森林中樹的數量（一般選取值較大）
抽取的屬性值m的大小。

思考

為什么要隨機抽樣訓練集？

如果不進行隨機抽樣，每棵樹的訓練集都一樣，那么最終訓練出的樹分類結果也是完全一樣。

為什么要有放回地抽樣？

如果不是有放回的抽樣，那么每棵樹的訓練樣本都是不同的，都是沒有交集的，這樣每棵樹都是“有偏的”，都是絕對“片面的”，也就是說每棵樹訓練出來都是有很大的差異的；而隨機森林最后分類取決于多棵樹（弱分類器）的投票表決。

【知道】隨機森林 API

sklearn.ensemble.RandomForestClassifier()

n_estimators：決策樹數量，(default = 10)

Criterion：entropy、或者 gini, (default = gini)

max_depth：指定樹的最大深度，(default = None 表示樹會盡可能的生長)

max_features="auto”, 決策樹構建時使用的最大特征數量

If "auto", then max_features=sqrt(n_features).
If "sqrt", then max_features=sqrt(n_features)(same as "auto").
If "log2", then max_features=log2(n_features).
If None, then max_features=n_features.

bootstrap：是否采用有放回抽樣，如果為 False 將會使用全部訓練樣本，(default = True)

min_samples_split： 結點分裂所需最小樣本數，(default = 2)

如果節點樣本數少于min_samples_split，則不會再進行劃分.
如果樣本量不大，不需要設置這個值.
如果樣本量數量級非常大，則推薦增大這個值.

min_samples_leaf： 葉子節點的最小樣本數，(default = 1)

如果某葉子節點數目小于樣本數，則會和兄弟節點一起被剪枝.
較小的葉子結點樣本數量使模型更容易捕捉訓練數據中的噪聲.

min_impurity_split: 節點劃分最小不純度

如果某節點的不純度(基尼系數，均方差)小于這個閾值，則該節點不再生成子節點，并變為葉子節點.
一般不推薦改動默認值1e-7。

【實踐】隨機森林泰坦尼克號生存預測

這泰坦尼克號案例實戰：

#1.數據導入
#1.1導入數據
import pandas as pd
#1.2.利用pandas的read.csv模塊從互聯網中收集泰坦尼克號數據集
titanic=pd.read_csv("data/泰坦尼克號.csv")
titanic.info() #查看信息
#2人工選擇特征pclass,age,sex
X=titanic[['Pclass','Age','Sex']]
y=titanic['Survived']
#3.特征工程
#數據的填補
X['Age'].fillna(X['Age'].mean(),inplace=True)
X = pd.get_dummies(X)
#數據的切分
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X,y,test_size=0.25,random_state=22)#4.使用單一的決策樹進行模型的訓練及預測分析
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier()
dtc.fit(X_train,y_train)
dtc_y_pred=dtc.predict(X_test)
dtc.score(X_test,y_test)#5.隨機森林進行模型的訓練和預測分析
from sklearn.ensemble import RandomForestClassifier
rfc=RandomForestClassifier(max_depth=6,random_state=9)
rfc.fit(X_train,y_train)
rfc_y_pred=rfc.predict(X_test)
rfc.score(X_test,y_test)#6.性能評估
from sklearn.metrics import classification_report
print("dtc_report:",classification_report(dtc_y_pred,y_test))
print("rfc_report:",classification_report(rfc_y_pred,y_test))

超參數選擇代碼:

# 隨機森林去進行預測
# 1 實例化隨機森林
rf = RandomForestClassifier()
# 2 定義超參數的選擇列表
param={"n_estimators":[80,100,200], "max_depth": [2,4,6,8,10,12],"random_state":[9]}
# 超參數調優
# 3 使用GridSearchCV進行網格搜索
from sklearn.model_selection import GridSearchCV
gc = GridSearchCV(rf, param_grid=param, cv=2)
gc.fit(X_train, y_train)
print("隨機森林預測的準確率為：", gc.score(X_test, y_test))

Adaboost

學習目標：

1、理解adaboost算法的思想

2、知道adaboost的構建過程

3、實踐泰坦尼克號生存預測案例

【知道】adaboost算法簡介

Adaptive Boosting(自適應提升)基于 Boosting思想實現的一種集成學習算法核心思想是通過逐步提高那些被前一步分類錯誤的樣本的權重來訓練一個強分類器。弱分類器的性能比隨機猜測強就行，即可構造出一個非常準確的強分類器。其特點是：訓練時，樣本具有權重，并且在訓練過程中動態調整。被分錯的樣本的樣本會加大權重，算法更加關注難分的樣本。

Adaboost自適應在于：“關注”被錯分的樣本，“器重”性能好的弱分類器:（觀察下圖）

（1）不同的訓練集--->調整樣本權重

（2）“關注”--->增加錯分樣本權重

（3）“器重”--->好的分類器權重大

（4）樣本權重間接影響分類器權重

主要過程演示如下：

AdaBoost算法的兩個核心步驟：

權值調整： AdaBoost算法提高那些被前一輪基分類器錯誤分類樣本的權值，而降低那些被正確分類樣本的權值。從而使得那些沒有得到正確分類的樣本，由于權值的加大而受到后一輪基分類器的更大關注。

基分類器組合： AdaBoost采用加權多數表決的方法。

分類誤差率較小的弱分類器的權值大，在表決中起較大作用。
分類誤差率較大的弱分類器的權值小，在表決中起較小作用。

AdaBoost 模型公式中

α 為模型的權重
m 為弱學習器數量
hi(x) 表示弱學習器
H(x) 輸出結果大于 0 則歸為正類，小于 0 則歸為負類。

AdaBoost 權重更新公式:

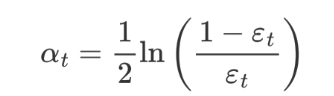
εt 表示第 t 個弱學習器的錯誤率

AdaBoost 樣本權重更新公式:

Zt 為歸一化值（所有樣本權重的總和）
Dt(x) 為樣本權重
αt 為模型權重。

【理解】 AdaBoost 構建過程

下面為訓練數數據，假設弱分類器由 x 產生，其閾值 v 使該分類器在訓練數據集上的分類誤差率最低，試用 Adaboost 算法學習一個強分類器。

構建第一個弱學習器

初始化工作：初始化 10 個樣本的權重，每個樣本的權重為：0.1
構建第一個基學習器：
1. 尋找最優分裂點
  1. 對特征值 x 進行排序，確定分裂點為：0.5、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5
  2. 當以 0.5 為分裂點時，有 5 個樣本分類錯誤
  3. 當以 1.5 為分裂點時，有 4 個樣本分類錯誤
  4. 當以 2.5 為分裂點時，有 3 個樣本分類錯誤
  5. 當以 3.5 為分裂點時，有 4 個樣本分類錯誤
  6. 當以 4.5 為分裂點時，有 5 個樣本分類錯誤
  7. 當以 5.5 為分裂點時，有 4 個樣本分類錯誤
  8. 當以 6.5 為分裂點時，有 5 個樣本分類錯誤
  9. 當以 7.5 為分裂點時，有 4 個樣本分類錯誤
  10. 當以 8.5 為分裂點時，有 3 個樣本分類錯誤
  11. 最終，選擇以 2.5 作為分裂點，計算得出基學習器錯誤率為：3/10=0.3
2. 計算模型權重: 1/2 * np.log((1-0.3)/0.3)=0.4236
3. 更新樣本權重：
  1. 分類正確樣本為：1、2、3、4、5、6、10 共 7 個，其計算公式為：e-αt，則正確樣本權重變化系數為：e-0.4236 = 0.6547
  2. 分類錯誤樣本為：7、8、9 共 3 個，其計算公式為：eαt，則錯誤樣本權重變化系數為：e0.4236 = 1.5275
  3. 樣本 1、2、3、4、5、6、10 權重值為：0.06547
  4. 樣本 7、8、9 的樣本權重值為：0.15275
  5. 歸一化 Zt 值為：0.06547 * 7 + 0.15275 * 3 = 0.9165
  6. 樣本 1、2、3、4、5、6、10 最終權重值為： 0.07143
  7. 樣本 7、8、9 的樣本權重值為：0.1667
4. 此時得到：

尋找最優分裂點：
1. 對特征值 x 進行排序，確定分裂點為：0.5、1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5
2. 當以 0.5 為分裂點時，有 5 個樣本分類錯誤，錯誤率為：0.07143 * 5 = 0.35715
3. 當以 1.5 為分裂點時，有 4 個樣本分類錯誤，錯誤率為：0.07143 * 1 + 0.16667 * 3 = 0.57144
4. 當以 2.5 為分裂點時，有 3 個樣本分類錯誤，錯誤率為：0.16667 * 3 = 0.57144
  
  。。。。。。
5. 當以 8.5 為分裂點時，有 3 個樣本分類錯誤，錯誤率為：0.07143 * 3 = 0.21429
6. 最終，選擇以 8.5 作為分裂點，計算得出基學習器錯誤率為：0.21429
計算模型權重：1/2 * np.log((1-0.21429)/0.21429)=0.64963
分類正確的樣本：1、2、3、7、8、9、10，其權重調整系數為：0.5222
分類錯誤的樣本：4、5、6，其權重調整系數為：1.9148
分類正確樣本權重值：
1. 樣本 0、1、2、、9 為：0.0373
2. 樣本 6、7、8 為：0.087
分類錯誤樣本權重值：0.1368
歸一化 Zt 值為：0.0373 * 4 + 0.087 * 3 + 0.1368 * 3 = 0.8206
最終權重：
1. 樣本 0、1、2、9 為：0.0455
2. 樣本 6、7、8 為：0.1060
3. 樣本 3、4、5 為：0.1667
此時得到：

構建第三個弱學習器

錯誤率：0.1820，模型權重：0.7514

【實踐】AdaBoost實戰葡萄酒數據

葡萄酒分為白葡萄酒和紅葡萄酒兩類。該分析涉及白葡萄酒，并基于數據集中顯示的13個變量/特征：固定酸度，揮發性酸度，檸檬酸，殘留糖，氯化物，游離二氧化硫，總二氧化硫，密度，pH值，硫酸鹽，酒精，質量等。為了評估葡萄酒的質量，我們提出的方法就是根據酒的物理化學性質與質量的關系，找出高品質的葡萄酒具體與什么性質密切相關，這些性質又是如何影響葡萄酒的質量。

import pandas as pd
df_wine = pd.read_csv('data/wine.data')
# 修改列名
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue', 'OD280/OD315 of diluted wines',
'Proline']
# 去掉一類(1,2，3)
df_wine = df_wine[df_wine['Class label'] != 1]
# 獲取特征值和目標值
X = df_wine[['Alcohol', 'Hue']].values
y = df_wine['Class label'].valuesfrom sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
# 類別轉化 (2,3)=>(0,1)
le = LabelEncoder()
y = le.fit_transform(y)
# 劃分訓練集和測試集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.4,random_state=1)from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
# 機器學習(決策樹和AdaBoost)
tree = DecisionTreeClassifier(criterion='entropy',max_depth=1,random_state=0)
ada= AdaBoostClassifier(base_estimator=tree,n_estimators=500,learning_rate=0.1,random_state=0)
from sklearn.metrics import accuracy_score
# 決策樹和AdaBoost分類器性能評估
# 決策樹性能評估
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))
# Decision tree train/test accuracies 0.845/0.854# AdaBoost性能評估
ada = ada.fit(X_train,y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print('Adaboost train/test accuracies %.3f/%.3f' % (ada_train,ada_test))
# Adaboost train/test accuracies 1/0.875

GBDT

學習目標：

掌握提升樹的算法原理思想
了解梯度提升樹的原理思想

【理解】提升樹（Boosting Tree）

梯度提升樹（Gradient Boosting Decision Tre）是提升樹（Boosting Decision Tree）的一種改進算法，所以在講梯度提升樹之前先來介紹一下提升樹。

假如有個人30歲，我們首先用20歲去擬合，發現損失有10歲，這時我們用6歲去擬合剩下的損失，發現差距還有4歲，第三輪我們用3歲擬合剩下的差距，差距就只有一歲了。如果我們的迭代輪數還沒有完，可以繼續迭代下面，每一輪迭代，擬合的歲數誤差都會減小。最后將每次擬合的歲數加起來便是模型輸出的結果。

【理解】梯度提升樹

梯度提升樹不再使用擬合殘差，而是利用最速下降的近似方法，利用損失函數的負梯度作為提升樹算法中的殘差近似值。

假設:

我們前一輪迭代得到的強學習器是：fi-1(x)
損失函數是：L(y,f?i?1(x))
本輪迭代的目標是找到一個弱學習器：hi(x)
讓本輪的損失最小化: L(y, fi(x))=L(y, fi?1(x)) + hi(x))

當采用平方損失函數時:

則:

損失函數為平方損失, 則每個樣本要擬合的負梯度為:

此時, 我們發現 GBDT 擬合的負梯度就是殘差，或者說對于回歸問題，擬合的目標值就是殘差。

如果我們的 GBDT 進行的是分類問題，則損失函數變為 logloss，此時擬合的目標值就是該損失函數的負梯度值。

【理解】GBDT例子

初始化弱學習器（CART樹）

我們通過計算當模型預測值為何值時，會使得第一個基學習器的平方誤差最小，即：求損失函數對 f(xi) 的導數，并令導數為0.

構建第一個弱學習器（CART樹）

由于我們擬合的是樣本的負梯度，即：

由此得到數據表如下：

上表中平方損失計算過程說明（以切分點1.5為例）：

切分點1.5 將數據集分成兩份 [5.56],[5.56 5.7 5.91 6.4 6.8 7.05 8.9 8.7 9. 9.05]

第一份的平均值為5.56 第二份數據的平均值為（5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05）/9 = 7.5011

由于是回歸樹，每份數據的平均值即為預測值，則可以計算誤差，第一份數據的誤差為0，第二份數據的平方誤差為 :

以 6.5 作為切分點損失最小，構建決策樹如下：

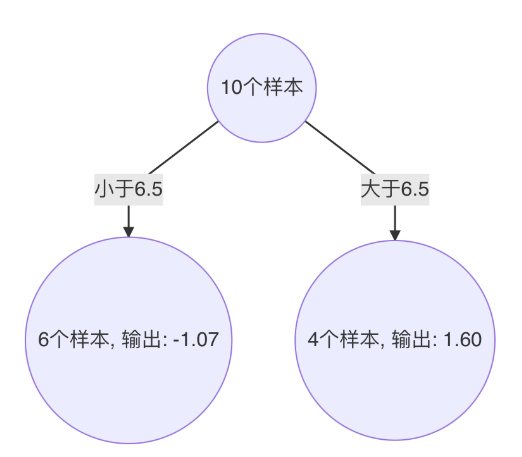
構建第二個弱學習器（CART樹）

以 3.5 作為切分點損失最小，構建決策樹如下：

構建第三個弱學習器（CART樹）

GBDT算法流程

1 初始化弱學習器（目標值的均值作為預測值）

2 迭代構建學習器，每一個學習器擬合上一個學習器的負梯度

3 直到達到指定的學習器個數

4 當輸入未知樣本時，將所有弱學習器的輸出結果組合起來作為強學習器的輸出

【實踐】泰坦尼克號案例實戰

該案例是在隨機森林的基礎上修改的，可以對比理解

#1.數據導入
#1.1導入數據
import  pandas as pd
#1.2.利用pandas的read.csv模塊泰坦尼克號數據集
titanic=pd.read_csv("../data/泰坦尼克號數據集.csv")
titanic.info() #查看信息
#2人工選擇特征pclass,age,sex
X=titanic[['Pclass','Age','Sex']]
y=titanic['Survived']
#3.特征工程
#數據的填補
X['Age'].fillna(X['Age'].mean(),inplace=True)
#數據的切分
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X,y,test_size=0.25,random_state=22)
#將數據轉化為特征向量
from sklearn.feature_extraction import DictVectorizer
vec=DictVectorizer(sparse=False)
X_train=vec.fit_transform(X_train.to_dict(orient='records'))
X_test=vec.transform(X_test.to_dict(orient='records'))
#4.使用單一的決策樹進行模型的訓練及預測分析
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier()
dtc.fit(X_train,y_train)
dtc_y_pred=dtc.predict(X_test)
print("score",dtc.score(X_test,y_test))
#5.隨機森林進行模型的訓練和預測分析
from sklearn.ensemble import RandomForestClassifier
rfc=RandomForestClassifier(random_state=9)
rfc.fit(X_train,y_train)
rfc_y_pred=rfc.predict(X_test)
print("score:forest",rfc.score(X_test,y_test))
#6.GBDT進行模型的訓練和預測分析
from sklearn.ensemble import GradientBoostingClassifier
gbc=GradientBoostingClassifier()
gbc.fit(X_train,y_train)
gbc_y_pred=gbc.predict(X_test)
print("score:GradientBoosting",gbc.score(X_test,y_test))
#7.性能評估
from sklearn.metrics import classification_report
print("dtc_report:",classification_report(dtc_y_pred,y_test))
print("rfc_report:",classification_report(rfc_y_pred,y_test))
print("gbc_report:",classification_report(gbc_y_pred,y_test))

XGBoost

XGBoost 是對GBDT的改進：

求解損失函數極值時使用泰勒二階展開
在損失函數中加入了正則化項
XGB 自創一個樹節點分裂指標。這個分裂指標就是從損失函數推導出來的。XGB 分裂樹時考慮到了樹的復雜度。

構建最優模型的方法是最小化訓練數據的損失函數 。

預測值和真實值經過某個函數計算出損失，并求解所有樣本的平均損失，并且使得損失最小。這種方法訓練得到的模型復雜度較高，很容易出現過擬合。因此，為了降低模型的復雜度，在損失函數中添加了正則化項，如下所示：：

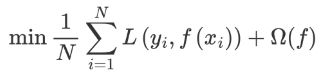
提高模型對未知數據的泛化能力。

【理解】XGboost的目標函數

XGBoost（Extreme Gradient Boosting）是對梯度提升樹的改進，并且在損失函數中加入了正則化項。

目標函數的第一項表示整個強學習器的損失，第二部分表示強學習器中 K 個弱學習器的復雜度。

xgboost 每一個弱學習器的復雜度主要從兩個方面來考量：

γT 中的 T 表示一棵樹的葉子結點數量，γ 是對該項的調節系數
λ||w||2 中的 w 表示葉子結點輸出值組成的向量，λ 是對該項的調節系數

模型復雜度的介紹

假設我們要預測一家人對電子游戲的喜好程度，考慮到年輕和年老相比，年輕更可能喜歡電子游戲，以及男性和女性相比，男性更喜歡電子游戲，故先根據年齡大小區分小孩和大人，然后再通過性別區分開是男是女，逐一給各人在電子游戲喜好程度上打分，如下圖所示：

就這樣，訓練出了2棵樹tree1和tree2，類似之前gbdt的原理，兩棵樹的結論累加起來便是最終的結論，所以：

小男孩的預測分數就是兩棵樹中小孩所落到的結點的分數相加：2 + 0.9 = 2.9。
爺爺的預測分數同理：-1 + 0.9 = -0.1。

具體如下圖所示：

如下樹tree1的復雜度表示為：

泰勒公式展開

我們直接對目標函數求解比較困難，通過泰勒展開將目標函數換一種近似的表示方式。接下來對 yi(t-1) 進行泰勒二階展開，得到如下近似表示的公式：

其中，gi 和 hi 的分別為損失函數的一階導、二階導：

化簡目標函數

我們觀察目標函數，發現以下兩項都是常數項，我們可以將其去掉。

我們再將 Ω(ft) 展開，結果如下：

這個公式中只有 ft ，該公式可以理解為，當前這棵樹如何構建能夠降低損失。

問題再次轉換

我們再次理解下這個公式表示的含義：

gi 表示每個樣本的一階導，hi 表示每個樣本的二階導
ft(xi) 表示樣本的預測值
T 表示葉子結點的數目
||w||2 由葉子結點值組成向量的模

現在，我們發現公式的各個部分考慮的角度不同，有的從樣本角度來看，例如：ft(xi) ，有的從葉子結點的角度來看，例如：T、||w||2。我們下面就要將其轉換為相同角度的問題，這樣方便進一步合并項、化簡公式。我們統一將其轉換為從葉子角度的問題：

例如：10 個樣本，落在 D 結點 3 個樣本，落在 E 結點 2 個樣本，落在 F 結點 2 個樣本，落在 G 結點 3 個樣本

D 結點計算： w1 * gi1 + w1 * gi2 + w1 * gi3 = (gi1 + gi2 + gi3) * w1
E 結點計算： w2 * gi4 + w2 * gi5 = (gi4 + gi5) * w2
F 結點計算： w3 * gi6 + w3 * gi6 = (gi6 + gi7) * w3
G 節點計算：w4 * gi8 + w4 * gi9 + w4 * gi10 = (gi8 + gi9 + gi10) * w4

gi ft(xi) 表示樣本的預測值，我們將其轉換為如下形式：

wj 表示第 j 個葉子結點的值
gi 表示每個樣本的一階導

hift2(xi) 轉換從葉子結點的問題，如下：

λ||w||2 由于本身就是從葉子角度來看，我們將其轉換一種表示形式：

我們重新梳理下整理后的公式，如下：

上面的公式太復雜了，我們令：

Gi 表示樣本的一階導之和，Hi 表示樣本的二階導之和，當確定損失函數時，就可以通過計算得到結果。

現在我們的公式變為：

對葉子結點求導

此時，公式可以看作是關于葉子結點 w 的一元二次函數，我們可以對 w 求導并令其等于 0，可得到 w 的最優值，將其代入到公式中，即可再次化簡上面的公式。

將 wj 代入到公式中，即可得到：

XGBoost的樹構建方法

該公式也叫做打分函數 (scoring function)，它可以從樹的損失函數、樹的復雜度兩個角度來衡量一棵樹的優劣。

這個公式，我們怎么用呢？

當我們構建樹時，可以用來選擇樹的最佳劃分點。

其過程如下：

對樹中的每個葉子結點嘗試進行分裂
計算分裂前 - 分裂后的分數：
1. 如果gain > 0，則分裂之后樹的損失更小，我們會考慮此次分裂
2. 如果gain< 0，說明分裂后的分數比分裂前的分數大，此時不建議分裂
當觸發以下條件時停止分裂：
1. 達到最大深度
2. 葉子結點樣本數量低于某個閾值
3. 等等...

【了解】XGboost API

bst = XGBClassifier(n_estimators, max_depth, learning_rate, objective)

【實踐】紅酒品質預測

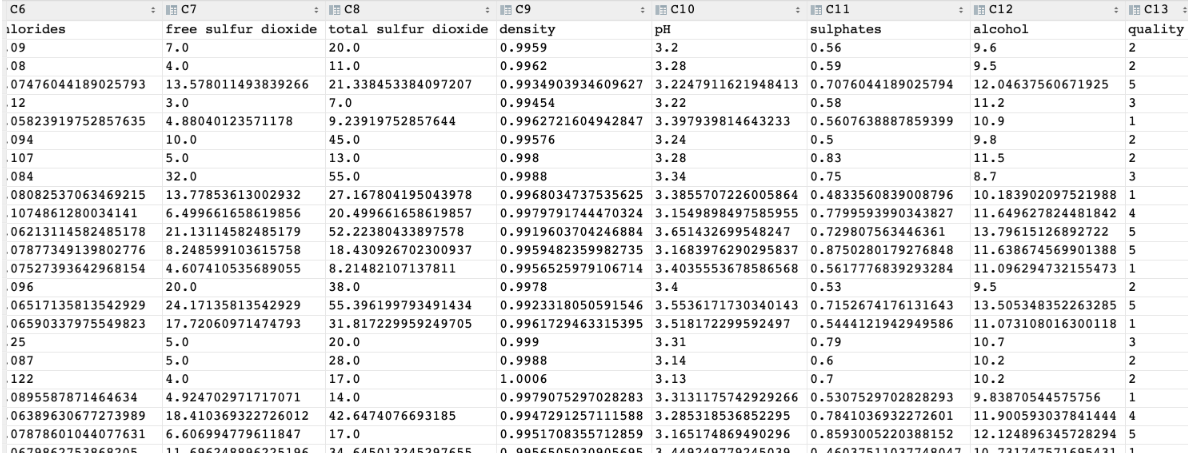
數據集介紹

數據集共包含 11 個特征，共計 3269 條數據. 我們通過訓練模型來預測紅酒的品質, 品質共有 6 個各類別，分別使用數字: 1、2、3、4、5 來表示。

案例實現

導入需要的庫文件

import joblib
import numpy as np
import xgboost as xgb
import pandas as pd
import numpy as np
from collections import Counter
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.model_selection import StratifiedKFold

數據基本處理

def test01():# 1. 加載訓練數據data = pd.read_csv('data/紅酒品質分類.csv')x = data.iloc[:, :-1]y = data.iloc[:, -1] - 3# 2. 數據集分割x_train, x_valid, y_train, y_valid = train_test_split(x, y, test_size=0.2, stratify=y, random_state=22)# 3. 存儲數據pd.concat([x_train, y_train], axis=1).to_csv('data/紅酒品質分類-train.csv')pd.concat([x_valid, y_valid], axis=1).to_csv('data/紅酒品質分類-valid.csv')

模型基本訓練

def test02():# 1. 加載訓練數據train_data = pd.read_csv('data/紅酒品質分類-train.csv')valid_data = pd.read_csv('data/紅酒品質分類-valid.csv')# 訓練集x_train = train_data.iloc[:, :-1]y_train = train_data.iloc[:, -1]# 測試集x_valid = valid_data.iloc[:, :-1]y_valid = valid_data.iloc[:, -1]# 2. XGBoost模型訓練estimator = xgb.XGBClassifier(n_estimators=100,objective='multi:softmax',eval_metric='merror',eta=0.1,use_label_encoder=False,random_state=22)estimator.fit(x_train, y_train)# 3. 模型評估y_pred = estimator.predict(x_valid)print(classification_report(y_true=y_valid, y_pred=y_pred))# 4. 模型保存joblib.dump(estimator, 'model/xgboost.pth')

模型參數調優

# 樣本不均衡問題處理
from sklearn.utils import class_weight
classes_weights = class_weight.compute_sample_weight(class_weight='balanced',y=y_train)
# 訓練的時候，指定樣本的權重
estimator.fit(x_train, y_train,sample_weight = classes_weights)
y_pred = estimator.predict(x_valid)
print(classification_report(y_true=y_valid, y_pred=y_pred))# 交叉驗證，網格搜索
train_data = pd.read_csv('data/紅酒品質分類-train.csv')
valid_data = pd.read_csv('data/紅酒品質分類-valid.csv')# 訓練集
x_train = train_data.iloc[:, :-1]
y_train = train_data.iloc[:, -1]# 測試集
x_valid = valid_data.iloc[:, :-1]
y_valid = valid_data.iloc[:, -1]spliter = StratifiedKFold(n_splits=5, shuffle=True)
# 2. 定義超參數
param_grid = {'max_depth': np.arange(3, 5, 1),'n_estimators': np.arange(50, 150, 50),'eta': np.arange(0.1, 1, 0.3)}
estimator = xgb.XGBClassifier(n_estimators=100,objective='multi:softmax',eval_metric='merror',eta=0.1,use_label_encoder=False,random_state=22)
cv = GridSearchCV(estimator,param_grid,cv=spliter)
y_pred = cv.predict(x_valid)
print(classification_report(y_true=y_valid, y_pred=y_pred))