程序中描述一副圖像，已知其橫向縱向的像素個數即可（×）

灰度直方圖能反映一副圖像各個灰度級像素占圖像的面積比（√）

從程序編寫的角度看，描述一副圖像的基本屬性通常包括其分辨率，即圖像的寬度和高度，用像素單位表示。

圖像灰度直方圖反映了灰度分布

一般來說，量化級別越高，圖像數據量越大；反之亦然（√）

圖像灰度直方圖除以圖像總像素數，得到的是歸一化直方圖（√）

從圖像的累計歸一直方圖，可以求出其對應的歸一化直方圖

圖像對灰度直方圖的關系是多對一，圖像到灰度直方圖是一一對應的。

從圖像的累計歸一直方圖，可以求出其對應的歸一化直方圖（√）

僅從一幅圖像的灰度直方圖，無法求出其歸一化直方圖和累計歸一直方圖（×）

????????對于一幅給定的灰度圖像，它的灰度直方圖是確定的。因為灰度直方圖是描述圖像中各個灰度級別像素的數量分布情況，而一幅灰度圖像的像素分布是確定的，因此其灰度直方圖也是確定的

圖像采樣的關鍵參數是__采樣間隔___

圖像量化的關鍵參數是____C_____

A.采樣頻率??????? B.采樣間隔??????? C、量化級數

采樣所獲得的圖像總像素的多少，通常稱為圖像的分辨率

MATLAB語句的if語句用___end_____結束條件

exit？

MATLAB中的for語句，和C語言同樣，用{}表示循環體的范圍(×)

if condition% 條件為真時執行的代碼塊
else% 條件為假時執行的代碼塊
end

matlab中的if-else語句,必須用兩個end對應其條件的結束（×）

if condition1% 執行條件1為真時的代碼
elseif condition2% 當條件1為假且條件2為真時執行的代碼
else% 當所有條件都不為真時執行的代碼
end

MATLAB中的 a:b:c，b代表增量，但其值可以是負數 (√)

MATLAB中自定義函數中，函數名和文件名必須一致(√)

MATLAB中自定義函數，關鍵字為function

有語句 x=0:0.1:1; y=x.*x; 執行后y(2)的值為__0.01____

由于 x 的步長為 0.1，因此 x 向量包含了從 0 到 1 的數，以 0.1 為步長，即包含了 11 個元素。因此 y 也有 11 個元素，每個元素是對應 x 元素的平方。

因此，要計算 y(2) 的值，我

們只需要查找 y 中索引為 2 的元素即可。由于 MATLAB 中的索引是從 1 開始的，所以 y(2) 對應 x 向量中索引為 2 的元素的平方。而 x(2) 是 0.1，所以 y(2) 就是 0.1 * 0.1，結果是 0.01。

有語句 x=0:0.1:1; s=size(x); 執行后s(2)的值為__11__

顯示圖像f的MATLAB語句是______A_____
A、imshow(f)??????? B、plot(f)

函數 imshow() 用于顯示圖像，而 plot() 則用于繪制二維圖形。

若有 x=0:0.01:3.14; y=sin(x); 將描繪已y為橫軸，縱軸值為x的曲線的matlab語句是__plot(y, x)_________;

灰度圖像對灰度直方圖間的對應關系是_一一___對應關系。?

若有x=[1 2 3], y=[4 5 6]; 則用matlab一條語句實現x和y對應元素相乘為 z = _x.*y_;

圖像增強包括空域（點運算（直方圖設計映射、均衡化、規定化）、模板）和頻域

另一種分類是點運算（映射、直方圖均衡化、規定化）和模板運算

平滑：設計一個濾波器

? （鄰域平均、均值濾波器（均等地位）、中值濾波（非線性濾波））? 實際上進行卷積運算

銳化：邊緣（圖像中的邊緣位于其中相鄰像素的灰度值發生顯著變化的位置，甚至是發生劇烈變化的地方。）

??? （3）高頻信號與低頻信號

??? ① 高頻信號：把圖像中變化劇烈的部分，例如邊緣和噪聲等，稱為高頻信號。

????? ②低頻信號：把圖像中像素值變化平緩的部分，稱為低頻信號。

點處理（灰度映射）包括直方圖均衡化、直方圖規定化、二值化

中值濾波可以消除孤立噪聲

圖像平滑處理的算法有中值濾波

中值濾波可以抽取圖像的邊緣 （×）

設有映射關系 x=0:1/255:1；lut=sqrt(x)；以及灰度值為uint8型的圖像f，以下說明正確的是 B

A.g=lut(f);可以完成映射? ? ? ? B.g=lut(f+1);可以完成映射? ? ? ? C.g=imfilter(f,lut);可以完成映射? ? ? ? D.經過lut映射后，圖像整體變暗

A.錯誤.lut(0)出錯，因為MATLAB數組索引不能為0。

C.imfilter函數用于在圖像上應用一個濾波器，而lut在這里是一個查找表，不是一個濾波器核。因此，imfilter(f, lut)并不是執行查找表映射的正確方法，而是試圖用查找表作為濾波器核在圖像f上進行卷積.

D.lut = sqrt(x)，這是一個在[0, 1]區間內單調增加的函數，但增加速率低于線性（因為對于0到1之間的任何值x，sqrt(x)都小于x），這意味著映射后的值會被壓縮到一個更窄的范圍內，使得暗的像素變得相對較亮，而亮的像素增亮的幅度小于暗的像素。因此，整體上圖像會看起來更亮，而不是變暗。

設已知有映射關系lut(1:256)，圖像f為uint8，利用MATLAB語言處理得到結果圖像g，則可以用____g=lut(f+1)_____

x=0:0.1:1; s=size(x);結果為11

設有映射關系 x=0:1/255:1；lut=x.*x；以及灰度值為uint8型的圖像f，以下說明正確的是 C

A.g=lut(f);可以完成映射? ? ? ? B.經過lut映射后，圖像整體變亮? ? ? ? C.g=lut(f+1);可以完成映射? ? ? ? D.g=imfilter(f,lut);可以完成映射

圖像空域灰度處理中主要有點運算和模板運算

圖像銳化和均值濾波等線性濾波，實質上是圖像和模板的___卷積_____運算。

設已知有映射關系lut(1:256)，圖像f為double，利用MATLAB語言處理得到結果圖像g，則可以用___f=uint8(f*255)______; g=lut(f+1);

采用模板[-1 1]主要檢測_______水平___方向的邊緣

設f為double型的灰度圖像，lut[1:256]為0到1的double型的單調遞增，當lut為灰度映射函數時，針對計算輸出圖像g的描述正確的是____先將f轉換為uint8型后，再利用lut(f+1)得到g_____

一般來說，采樣間距越大，圖像數據量越______小___。反之也然。

matlab語句 x=0:0.01:1; 則x(1)和x(100)的值分別為___0___，___0.99_______

若有x=[1 2 3], y=[4 5 6];
執行程序段
if x(2)>2
?x(2)=0
end;
z = x - y;
后，z的值為：_____-3______? __-3_________? _____-3_____;

設f為uint8型的灰度圖像，lut(1:256)為double型的單調遞增，當lut為灰度映射函數時，輸出圖像g=____lut(f+1)__________;

設f為uint8型的灰度圖像，lut[1:256]為uint8型的單調遞增，當lut為灰度映射函數時，輸出圖像g=______lut(f+1)________;

1.設a和b均為二維矩陣，并有sa=size(a);sb=size(b); 則通過matlab圖像濾波器處理后的y=imfilter(a,b); 其大小，即[sx, sy] = size(y); 則sx=_____sa(1)___; sy=__sa(2)____;

MATLAB的圖像處理函數中，圖像線性濾波，比如加權平均濾波，可以用___imfilter________

設[sxa sya]=size(a);[sxb syb]=size(b); 則通過matlab圖像濾波器處理后的y=imfilter(a,b); 其大小，即[sx, sy] = size(y); 則sx=___sxa_____; sy=___sya___;

設圖像f的灰度值為double型，映射關系為lut，則結果圖像 g = lut( uint8( ____f*255+1_____ )? );

經Sobel算子處理后，可得到圖像的____________邊緣\輪廓______________________。

clc;
clear all;
close all;
f=zeros(256,256);
f(80:170,80:170)=1;
figure;
imshow(f);
imwrite(f,'bcw.jpg')

clc;
clear all;
close all;
f=zeros(50,256);
for i=1:256
??? f(:,i)=i-1;
end;
f=uint8(f);
figure;
imshow(f);
imwrite(f,'btw.jpg')

close all;
clear all;
clc;
f=imread('lena.jpg');
g=f';%矩陣轉置
figure;
subplot(1,2,1);imshow(f);
subplot(1,2,2);imshow(g);
imwrite(g,'lena90.jpg')

f=imread('lena.jpg');
g=imread('lenamirror.jpg');
[sx sy]=size(f);
[sx sy]=size(f);
fg(1:sx,1:sy)=f;
fg(1:sx,sy+1:2*sy)=g;
figure;
imshow(fg),title('lena2.jpg');

f=imread('lena.jpg');
g=f;
[sx sy]=size(f);
for i=16:16:sxg(i,:)=0;
end;
figure;
subplot(1,2,1);imshow(f);
subplot(1,2,2);imshow(g);
imwrite(g,'lenanoise1.jpg');

clc;
clear all;
close all;
f=zeros(256);
f(1:128,1:128)=1;
f(128:256,128:256)=1;
figure;
imshow(f);
imwrite(f,'bw1.jpg')

圖像lena.jpg為uint8類型的灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.利用直方圖均衡化增強其對比度；
2.在同一窗口內，輸出原圖和結果圖。

fnm='lena.jpg';
f = imread(fnm);%讀入圖像 
g = histeq(f); % 直方圖均衡化 figure; 
subplot(121);imshow(f);title([fnm, ':原圖']); 
subplot(122);plot(h);title([fnm,':結果圖']); 

圖像lena.jpg為uint8類型的灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.計算直方圖、歸一化直方圖和累積歸一直方圖;
2.在一個輸出窗口內，輸出原圖及三個直方圖。

fnm='lena.jpg';
f=imread(fnm);%讀入圖像 
h=imhist(f); %求直方圖
[sx sy]=size(f);
h1 = h/sx/sy;  %歸一化直方圖
H1=cumsum(h1);  %歸一累計直方圖 
figure; 
subplot(221);imshow(f);title([fnm, ':原圖']); 
subplot(222);plot(h);title([fnm,':直方圖']); 
subplot(223);plot(h1);title([fnm,':歸一化直方圖']); 
subplot(224);plot(H1);title([fnm,':累計歸一直方圖']);

圖像lena.jpg為uint8類型的灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.計算負片并在一個輸出窗口內輸出原圖和負片；
2.將負片圖像保存到文件“lena_ng.jpg”中。

f=imread('lena.jpg');
g=255-f;%負片  
figure; 
subplot(121);imshow(f); title('原圖');
subplot(122);imshow(g); title('負片');imwrite(g,"lena_ng.jpg");

圖像lena.jpg為uint8類型的灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.利用3*3的拉普拉斯算子實現圖像銳化；（? h = [ 0 -1 0; -1 5 -1; 0 -1 0]);
2.在一個窗口中輸出原圖和銳化后的圖像。

f=imread('lena.jpg');
h = [ 0 -1 0; -1 5 -1; 0 -1 0];
g = imfilter(f,h);
figure;
subplot(1,2,1);imshow(fn);title('原圖');
subplot(1,2,2);imshow(g);title('銳化后');

圖像lenanoise.jpg為uint8類型的帶有椒鹽噪聲灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.利用3*3的均值濾波模板除噪；
2.在一個窗口中輸出原圖和濾波后的圖像。

f = imread('lenanoise.jpg');
a=3;
h = ones(a)/a/a;  
g = imfilter(f,h); figure;
subplot(1,2,1); imshow(f); title('原圖'); subplot(1,2,2); imshow(g); title(' 除噪后'); 

圖像lenanoise.jpg為uint8類型的帶有椒鹽噪聲灰度圖像，用matlab語言設計程序，對該圖像，完成如下功能：
1.利用3*3窗口的中值濾波模板除噪；
2.在一個窗口中輸出原圖和濾波后的圖像。

常用的灰度內插方法有最近鄰、雙線性和三次內插 （√）

分割-閾值處理

閾值分割：二值化

閾值分割，確定閾值是關鍵.

閾值分割法是空域處理中的“點運算”的一種。

分為人工選擇閾值和自動選擇閾值。

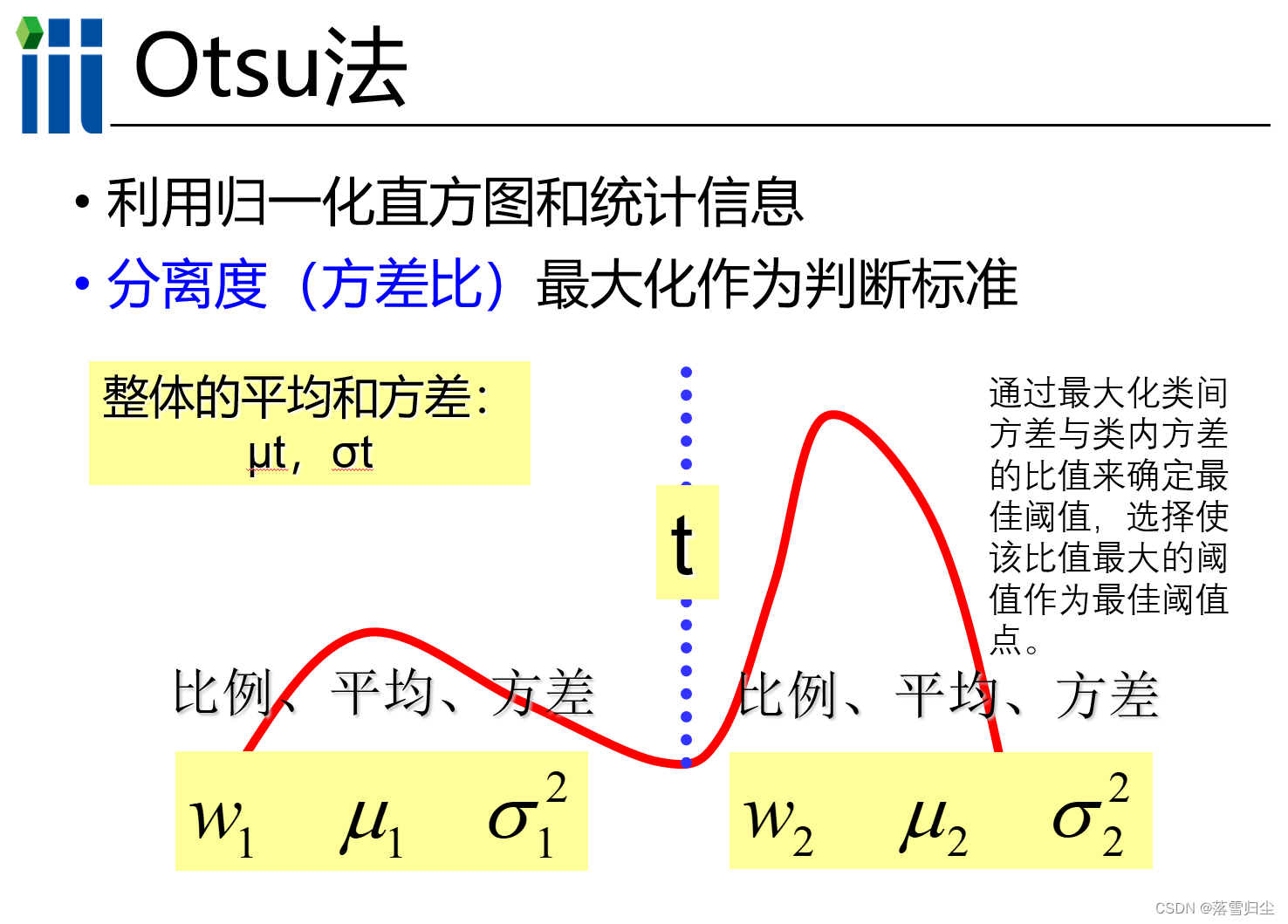
otsu法確定二值化閾值，將圖像灰度總方差最大化 （×）

程序實例如下：

I = imread('coins.png');subplot(121);imshow(I);title('原始圖像');

level = graythresh (I);? % 閾值

BW = im2bw(I,level);? % 二值化

subplot(122);imshow(BW);title('Otsu方法二值化圖像');

迭代法

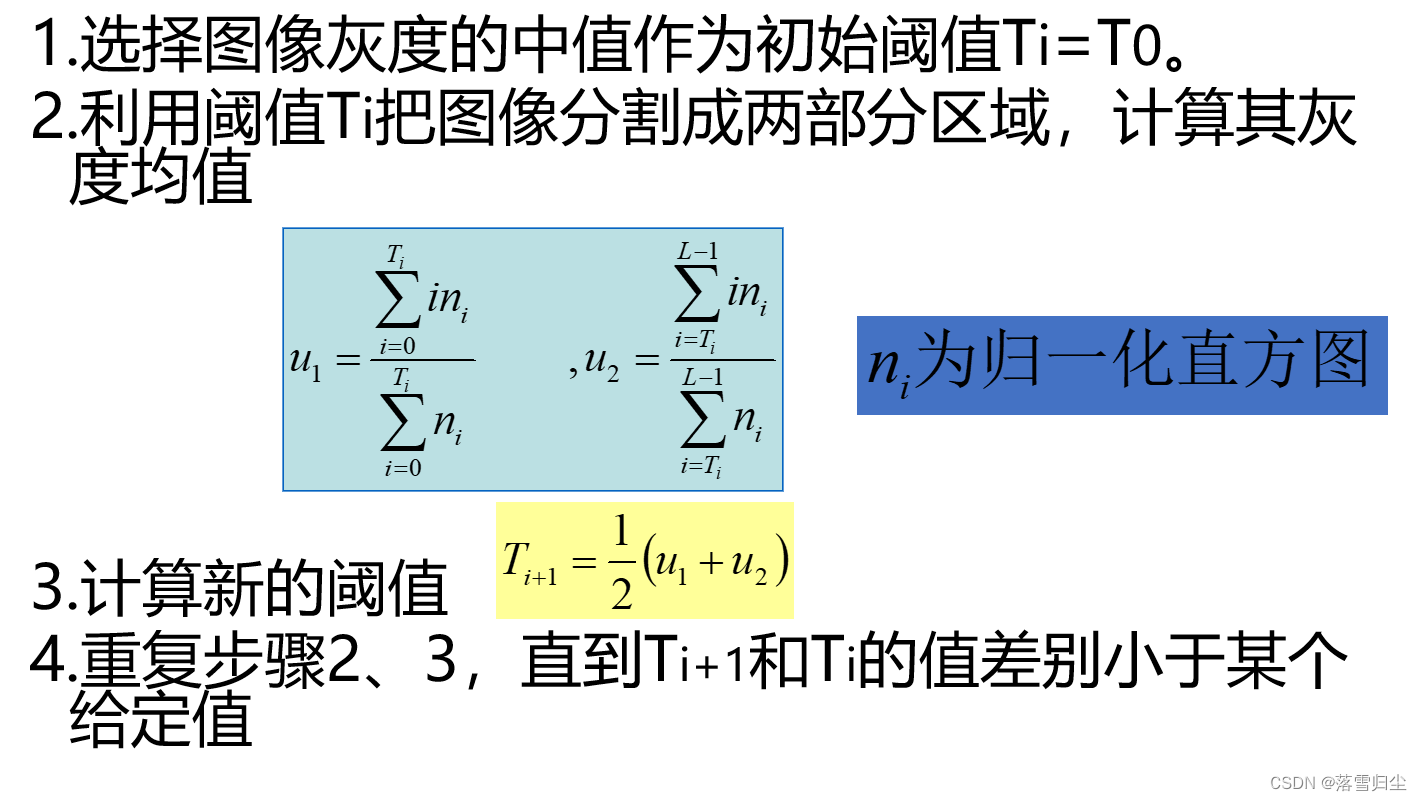
?迭代法確定二值化閾值，初始值如何給定并不重要，重要的是迭代方法 （×）

百分比法

圖像增強

??????? 圖像的直方圖增強處理方法，就是一種通過把原始圖像的灰度直方圖，從相對比較集中的某個灰度區間變成在全部灰度范圍內的均勻分布，來進行圖像增強的方法。

直方圖均衡

1. ?直方圖均衡的基本思想

???????? 所謂直方圖均衡，就是對于一幅已知灰度概率分布的灰度圖像，通過擴大該圖像中像素個數較多的灰度級別的分布范圍，縮減其像素個數較少的灰度級別的分布范圍，使該圖像的直方圖變換成具有均勻灰度概率分布的新圖像，以此來達到增加該圖像的對比度的圖像增強技術和方法。

1. ?直方圖均衡的基本思想

? 直方圖均衡即是找一種變換，使具有任意概率分布密度的直方圖的圖像，變換成接近于均勻概率分布密度的直方圖的圖像。

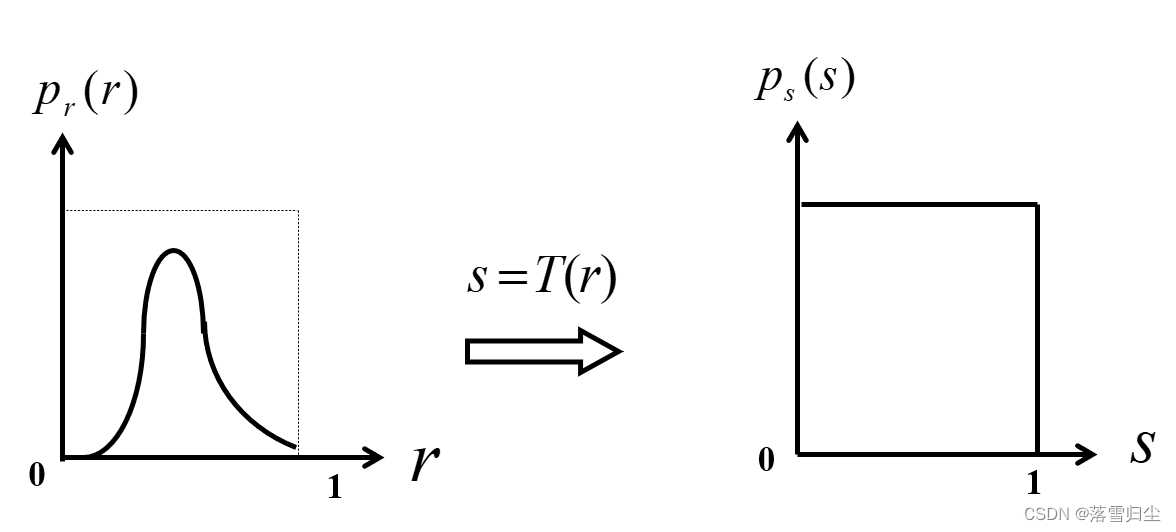
問題：

???? 直方圖均衡化方法為什么能增強圖像？

?????? 直方圖均衡化處理后，原來像素值相對比較集中的一些像素，會被分配到別的灰度值上去，處理后灰度范圍變大，對比度變大，清晰度變大，所以能有效增強圖像。

直方圖的規定化

??? 直方圖均衡方法雖然能顯著地增強圖像的對比度。但由于該方法總是僅產生近于似均勻分布的直方圖結果，而且其增強效果不易控制，所以在某些特定的情況下，必然限制了其效能的發揮和應用。

??? 實際應用中，有時可能需要的是具有某種特定形狀的直方圖的圖像，以便有選擇地對圖像中某個特定的灰度級范圍進行增強。

??? 直方圖規定化就是一種把已知直方圖的圖像變換成具有某種期望的直方圖的圖像增強方法。

圖像增強包括空域（點運算（直方圖設計映射、均衡化、規定化）、模板）和頻域

另一種分類是點運算（映射、直方圖均衡化、規定化）和模板運算

平滑：設計一個濾波器

? （鄰域平均、均值濾波器（均等地位）、其他（不是均等地位））? 實際上進行卷積運算

基于空間平滑濾波的圖像增強方法

完成以下圖像處理效果,首選頻域處理

A.圖像的二值化? ? ? ? B.消除圖像中的規律噪聲

B.使用頻域處理來消除圖像中規律噪聲的步驟：

1. 傅里葉變換：首先對圖像進行傅里葉變換，將其從空間域轉換到頻域。在頻域中，圖像的所有信息都表現為頻率成分。

2. 識別并處理噪聲：在頻域圖像中，規律噪聲（如條紋、網格等）通常表現為特定位置的尖銳、亮點或頻率成分。通過觀察頻譜圖，可以定位這些代表噪聲的頻率成分。

3. 應用帶阻濾波器：對確定的噪聲頻率成分應用帶阻濾波器或陷波濾波器來削弱或移除這些噪聲成分。帶阻濾波器允許大多數頻率正常通過，只阻斷一定范圍內的頻率。

4. 傅里葉逆變換：處理完噪聲后，使用傅里葉逆變換將頻域圖像轉換回空間域。轉換后的圖像將展現出減少或消除了規律噪聲的效果。

對于A選項——圖像的二值化——這通常是在空間域中更容易和直接完成的處理。二值化處理通常涉及到設置一個閾值，將圖像中的像素值根據這個閾值轉換為0或255（黑或白），這在空間域中實現起來比較簡單和直觀。

fft2 傅里葉變換? ? ? ? ifft2 反傅里葉變換

已知Ft為某圖像的傅里葉變換，得到其相位P的MATLAB語句為 P = angle(Ft);（以弧度為單位）.????????這行代碼會計算 Ft 中每個元素的相位（以弧度為單位），結果存儲在 P 中。

已知Ft為某圖像的傅里葉變換，得到其振幅（也即復數的模）Amp的MATLAB語句為 Amp = abs(Ft);????????這行代碼會計算 Ft 中每個元素的振幅，結果存儲在 Amp 中。

圖像空域灰度處理中的模板處理，其計算實質上就是卷積運算.

卷積定理確保了頻域處理可以直接相乘，即 .*??

圖像頻域處理中主要有高通、低通、帶通和帶阻四種處理.

高通：圖像邊緣或輪廓檢測。

帶阻：可除有規律的噪聲。

低通：可除噪聲的同時，使得結果圖像變模糊。

Why？

1. 頻域表示：圖像的傅里葉變換將其從空間域轉換到頻域，在這個變換后的表示中，圖像的信息分布在不同的頻率上。低頻分量通常對應于圖像的主要形狀和大致輪廓，而高頻分量則包括邊緣、紋理細節和噪聲。

2. 低通濾波器的作用：

   • 濾除高頻成分：低通濾波器允許低頻成分通過，同時阻斷或減弱高頻成分。高頻通常包含了圖像的細節和噪聲。通過減弱這些高頻分量，噪聲得以減少，因為許多常見的圖像噪聲（如鹽和胡椒噪聲、電子噪聲等）都表現為高頻特性。
   • 導致模糊：當你去除或減弱圖像中的高頻部分，不僅噪聲得到抑制，圖像中銳利的邊緣和細節也會受到影響，因為這些也是由高頻分量表示的。結果，圖像的邊緣和細節變得不那么明顯，從而使整體圖像看起來更模糊。

3. 視覺效果：在視覺上，去除高頻細節后，圖像中的過渡變得更加平滑，這導致了模糊的視覺效果。這在一些應用中是可取的，比如在美容攝影或特定類型的藝術效果中，但在需要保持圖像清晰度的應用中，則可能不理想。

頻域處理中，希望得到輪廓信息，可用__高通__

復習

圖像空域處理和圖像頻域處理的概念、區別與聯系

概念

1. 空域處理：

   • 空域處理直接在圖像平面上進行，處理的是圖像的像素值。常見的空域處理技術包括圖像增強（如對比度調整）、濾波（如平滑和銳化）、邊緣檢測等。

2. 頻域處理：

   • 頻域處理首先需要將圖像從空域轉換到頻域，常通過傅里葉變換實現。在頻域中，圖像表示為頻率的組合，這樣可以分析和處理圖像中的周期性和方向性特征。頻域處理的例子包括低通濾波、高通濾波等。

區別

• 處理方式：

  • 空域處理關注像素級操作，如修改像素值或根據鄰域像素值進行計算。
  • 頻域處理通過轉換圖像到頻率空間，關注整體的頻率分布和圖像的全局特征。

• 工具和方法：

  • 空域使用的工具較直觀，如各種空間濾波器。
  • 頻域處理需要使用數學變換（如傅里葉變換）來實現圖像的頻域分析和修改。

• 性能和效果：

  • 空域處理操作通常更快，適用于實時系統。
  • 頻域處理在進行全局性調整（如頻率過濾）時更有效，但計算成本較高。

聯系

• 互相轉換：

  • 空域和頻域是可以相互轉換的。通過傅里葉變換將圖像從空域轉到頻域進行處理，再通過逆傅里葉變換返回到空域。

• 互補性：

  • 在某些情況下，空域和頻域處理可以結合使用，以利用各自的優勢。例如，在頻域進行噪聲削減后，再在空域進行局部的細節增強。

• 目標相同：

  • 不論是空域處理還是頻域處理，最終的目標都是改善圖像質量或提取圖像特征，只是處理的方法和視角不同。

    概念

  • 空域處理：

    • 空域處理直接在圖像平面上進行，處理的是圖像的像素值。常見的空域處理技術包括圖像增強（如對比度調整）、濾波（如平滑和銳化）、邊緣檢測等。

  • 頻域處理：

    • 頻域處理首先需要將圖像從空域轉換到頻域，常通過傅里葉變換實現。在頻域中，圖像表示為頻率的組合，這樣可以分析和處理圖像中的周期性和方向性特征。頻域處理的例子包括低通濾波、高通濾波等。

  • 區別

  • 處理方式：

    • 空域處理關注像素級操作，如修改像素值或根據鄰域像素值進行計算。
    • 頻域處理通過轉換圖像到頻率空間，關注整體的頻率分布和圖像的全局特征。

  • 工具和方法：

    • 空域使用的工具較直觀，如各種空間濾波器。
    • 頻域處理需要使用數學變換（如傅里葉變換）來實現圖像的頻域分析和修改。

  • 性能和效果：

    • 空域處理操作通常更快，適用于實時系統。
    • 頻域處理在進行全局性調整（如頻率過濾）時更有效，但計算成本較高。

  • 聯系

  • 互相轉換：

    • 空域和頻域是可以相互轉換的。通過傅里葉變換將圖像從空域轉到頻域進行處理，再通過逆傅里葉變換返回到空域。

  • 互補性：

    • 在某些情況下，空域和頻域處理可以結合使用，以利用各自的優勢。例如，在頻域進行噪聲削減后，再在空域進行局部的細節增強。

  • 目標相同：

    • 不論是空域處理還是頻域處理，最終的目標都是改善圖像質量或提取圖像特征，只是處理的方法和視角不同。

圖像空域處理中的圖像銳化處理本質上是頻域處理中的高通處理。

圖像空域處理中的均值濾波處理本質上是頻域處理中的低通處理。

e.g.?

自然圖像的大部分信息集中在低頻（√）

圖像銳化除了在空域進行外，可以在頻域進行（√）

圖像除噪聲可在空域進行外，也以在頻域進行（√）

理想低通濾波和高斯低通濾波后結果圖像的最大區別是有無振鈴效應（√）

理想高通濾波和高斯高通濾波后結果圖像的最大區別是有無振鈴效應（√）

理想濾波器和高斯濾波器在圖像處理中都用于頻域濾波，但它們的設計和效果有顯著的區別，其中最顯著的區別之一確實包括振鈴現象。這些濾波器的不同及其原因：

理想濾波器

• 定義：理想濾波器（低通或高通）具有一個固定的截止頻率，所有低于或高于此頻率的成分被完全通過或完全阻斷。這種濾波器的頻率響應在截止頻率處是不連續的。
• 特點：
  • 濾波效果非常明顯，因為它完全消除或保留特定頻率范圍內的信號。
  • 由于其硬切換特性，在時域中表現為較長的振鈴現象。

高斯濾波器

• 定義：高斯濾波器使用高斯函數作為其基礎，其響應曲線在頻域中呈高斯分布形態，頻率從中心向外逐漸下降。
• 特點：
  • 濾波效果更為平滑，因為頻率響應的過渡更加漸進。
  • 在時域中導致的振鈴現象較小，因為高斯函數的響應在時域也是高斯分布，無突變。

振鈴現象的原因

• 振鈴現象：在圖像處理中，振鈴現象通常表現為在邊緣附近出現的假影或波紋。這是由于頻域濾波器在時域中引入的非理想響應造成的。
• 理想濾波器的振鈴：理想濾波器由于其在截止頻率處的硬切換，其時域響應是一個Sinc函數，這種函數在理論上無限長，并在主瓣之外有許多小瓣，這導致顯著的振鈴現象。
• 高斯濾波器的減少振鈴：高斯濾波器的頻率響應在整個頻率范圍內平滑過渡，沒有突變點，因此其時域響應也是平滑的高斯形狀，這大大減少了振鈴現象。

總結來說，理想濾波器和高斯濾波器最大的區別之一是在于振鈴現象的顯著程度，這主要由它們在頻域的響應特性決定。理想濾波器由于其切斷特性在實際應用中容易產生較強的振鈴效應，而高斯濾波器則因其平滑的過渡性質而廣泛應用于需要減少圖像失真的場景。

下列二值化和灰度直方圖的關系敘述錯誤的是？B

? ? ? ? A.通常灰度直方圖的雙峰對應于圖像的前景和背景區域

? ? ? ? B.通過灰度直方圖可以知道二值化的最佳閾值

? ? ? ? C.灰度直方圖對二值化有很好的指導意義

? ? ? ? D.二值化求最佳閾值的過程通常包含分析直方圖的步驟

下列關于Otsu算法中“類間方差（between-classes variance）”的描述錯誤的是？B

? ? ? ? A.類間方差達到最大的情況下即為最優二值化值

? ? ? ? B.類間方差達到最小的情況下即為最優二值化值

? ? ? ? C.類間方差有機結合了前景和背景信息，是評價信息量多少的一個評價函數

? ? ? ? D.類間方差是根據前景部分的方差和背景部分的方差計算得到的

關于圖像縮小處理，下列說法正確的是：（ D ）
A、圖像的縮小只能按比例進行。
B、 利用基于等間隔采樣的圖像縮小方法對圖像進行處理時，不需要計算出采樣間隔。
C、圖像的縮小只能按不比例進行。
D、 圖像的縮小是從原始圖像中選擇合適的像素點，使圖像縮小后可以盡量保持原有圖像的概貌特征不丟失

下列關于二值形態學算法敘述錯誤的是？（ B ）

? ? ? ? A.通過開閉運算的結合可以出去圖像中的椒鹽噪聲

? ? ? ? B.對圖像進行重復的開操作會不斷產生新的不同的結果

? ? ? ? C.二值形態學操作包括了二值膨脹、二值腐蝕以及開閉運算

? ? ? ? D.二值膨脹可以使圖像的前景區域擴大
?

根據傅里葉變換的共軛對稱性，只需半個周期的變換就可以獲得整個變換的頻譜（√）

根據傅里葉變換的周期性，只需一個周期的變換就可以獲得整個變換的頻譜（√）

圖像形態學的膨脹操作（Dilation）可以使圖像中的對象擴展 變大。

自然界中的絕大多數的顏色都可看作是由紅、黃、藍三種顏色組合而成。 （×） 自然界中的絕大多數的顏色都可以分解成紅、綠、藍這三種顏色.

目前常用的彩色模型可分成兩類：

???????? （1）面向諸如彩色監視器、彩色視頻攝像機和彩色打印機的硬件設備。

???????? ????????主要有RGB模型、CMY（青、品紅、黃）模型和CMYK（青、品紅、黃、黑）模型。

???????????????? RGB模型主要用于彩色監視器和彩色視頻攝像機； CMYK主要用于彩色打印機。

???????? （2）面向諸如彩色動畫圖形創作等的彩色處理應用。面向彩色處理應用的模型主要是HSI模型（hue-saturation-intensity，即色調、亮度和飽和度）。

??? HSI（hue-saturation-intensity）彩色模型比較適合于人用色調（H）、飽和度（S）和亮度（I）描述被觀察物體顏色的解釋，對于開發基于彩色描述的圖像處理方法是一個理想的工具。

人眼對綠色的感知最敏銳（√）

對RGB各個R/G/B分量，進行同樣的處理，稱為___真/全___彩色處理。【一個漢字】

將彩色圖像轉換為灰度圖像的實質，就是通過對圖像R、G、B分量的變換，使得每個像素點的R、G、B分量值相等。（√）

計算機顯示器采用_RGB_彩色模型。

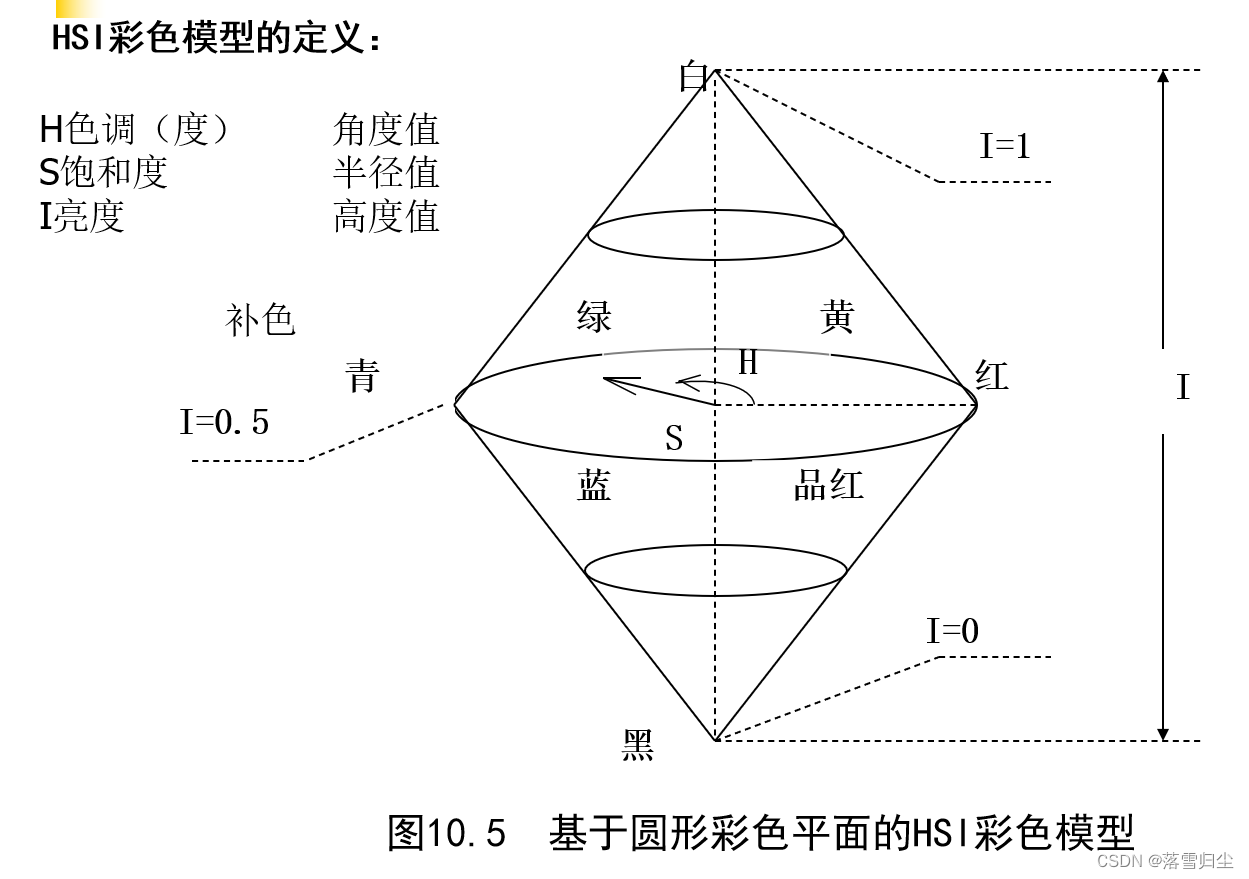
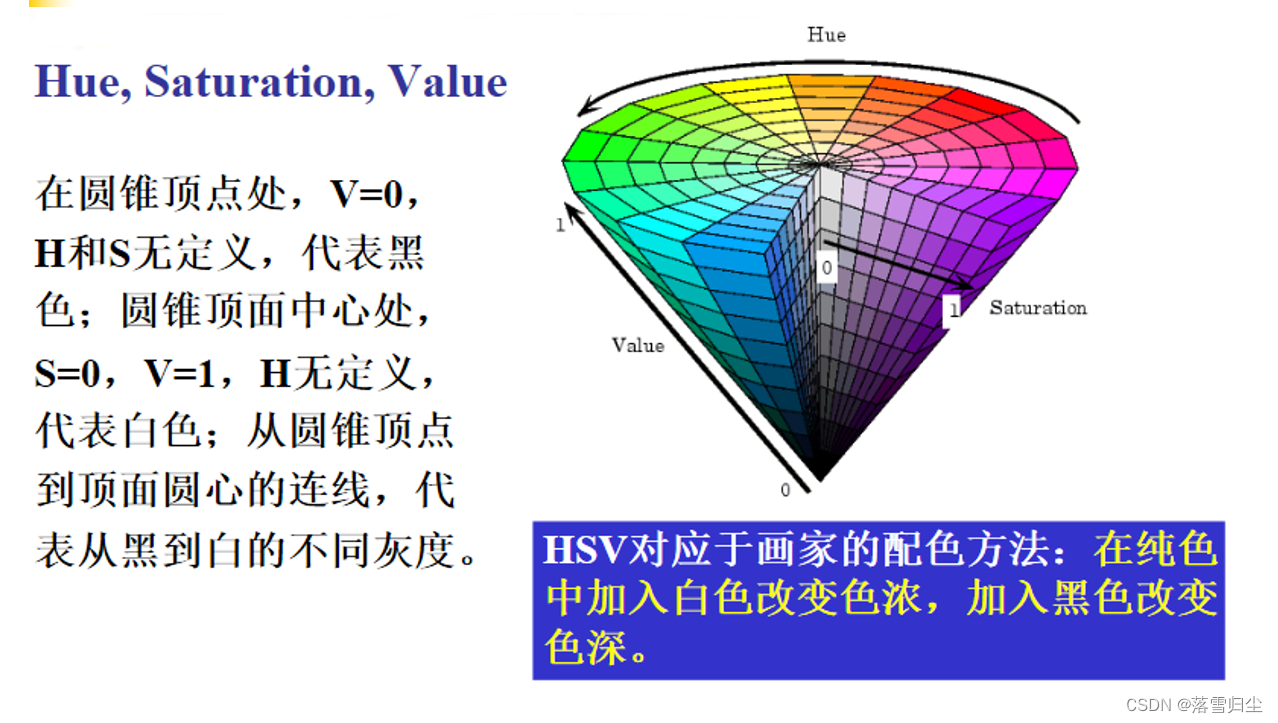
HSV彩色模型中的S是_彩度_,H是_色相_.

將rgb的圖像，轉換到視覺模型下的matlab函數是rgb2hsv.

彩色模型HSV下，常見處理方法有加法和乘法。對色相H的處理是_加_法。

彩色模型HSV下，常見處理方法有加法和乘法。對飽和度S的處理是_乘法 。

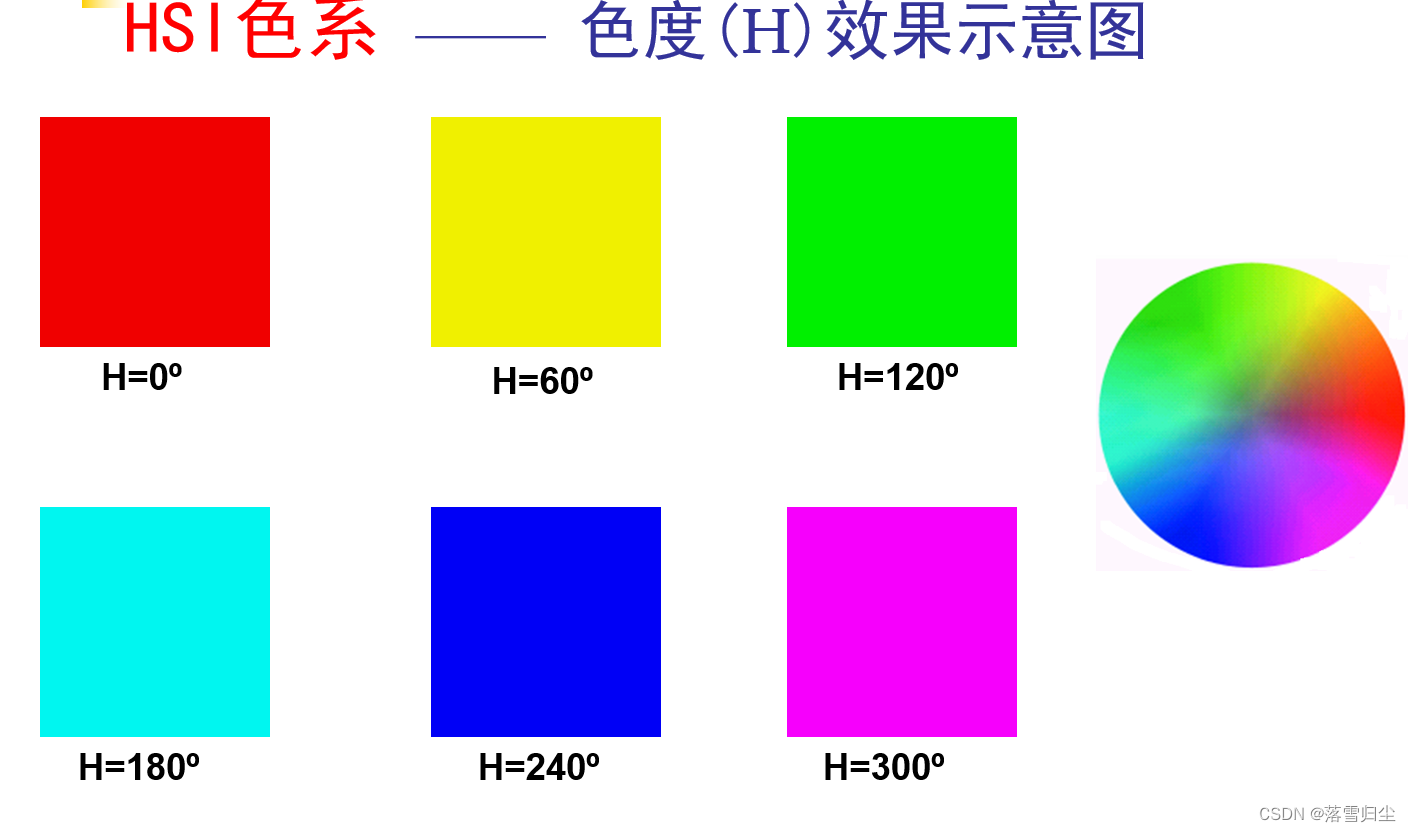
RGB彩色模型下的圖像數據，轉換為CMYK彩色模型下時，無論何種軟件其轉換結果是唯一的 （×）?

RGB彩色模型下的圖像數據，轉換為CMYK彩色模型下時，其轉換方法根據不同商家可以有多種（√）

印刷圖像采用哪一種彩色模型 _CMY / CMYK_?

NTSC和PAL制下，對應的彩色模型分別是：YIQ 和 YUV

YIQ為PAL制的彩色空間（×）

彩色空間YIQ變換為RGB，MATLAB中已有函數為：ntsc2rgb（√）

NTSC制下，傳輸彩色電視信號，使用的是_Y_、I和Q。

彩色模型YIQ下，一般情況對其Y、I和Q各個波段，采用完全相同的處理方法 （×）

彩色模型Yuv下，一般情況對其Y、u和v各個波段，采用完全相同的處理方法 （×）

YUV色彩空間可用彩色圖像壓縮 （√）

彩色模型HSV/HSI下，對飽和度S的常見處理方法是加一個度數（×）

設圖像f為rgb模型下的彩色圖像，利用MATLAB語句得到其綠色波段的語句為 g = ____f(:,:,2)____

圖像形態學中常用的一種形態學操作是（ 開運算 ），用于去除小于該結構元素的區域。

RGB轉換為灰度圖像G，其變換式為G =____0.3___*R+____0.6___*G+___0.1_____*B。【保留小數點后一位】

RGB轉換為灰度圖像G時，B所占比率最大，可達到約60%（×）

RGB轉換為灰度圖像G時，G所占比率最大，可達到約60%（√）

RGB轉換為灰度圖像G時，因為R紅色比較鮮艷，所以R所占比率最大（×）

YUV或YIQ模型下，比較亮度信息，人眼對色差信息的敏感程度較低，所以可以對色差信息直接縮小其大小（√）

在彩色圖像處理中，常使用HSI或HSV模型，它適于做圖像處理的原因是：色調與飽和度的概念與人的感知聯系緊密（√）

彩色模型HSV/HSI下，對色相H的常見處理方法是加一個度數（√）

彩色模型HSV/HSI下，一般情況下，對其HSV/HSI各個波段采用不同的處理方法（√）

MATLAB環境下，將rgb圖像f轉換為hsv的函數是 hsvx = _rgb2hsv(f)_;

設已知rgb圖像f及其對應的YIQ數據fx，為了得到f的灰度信息（即無彩的灰度圖像），可以用 g=_fx(:,:,3)_;

設已知rgb圖像f及其對應的hsv數據fx，為了得到f的灰度信息（即無彩的灰度圖像）,可以用 g=_fx(:,:,3)_

進行幾何變換和幾何校正時，最近鄰插值的坐標可用四舍五入來實現 （√）