我們在Scikit-learn對K-means假設的調查中探索了揭示算法優勢和局限性的場景。我們研究了K-means對不正確的聚類大小的敏感性，它在各向異性分布中面臨的困難，它在不同的聚類方差中面臨的困難，以及使用合成數據集的大小不均勻的聚類問題。我們希望這些假設的這種可視化表示將澄清K-means的適用性，并強調選擇特定于數據特征的聚類算法的重要性。

K-Means聚類

一種稱為K-means聚類的無監督機器學習技術用于根據數據中的相似性模式將數據集劃分為離散的組或聚類。該方法包括迭代地將數據點分配到聚類中，并優化每個聚類的質心，以減少每個數據點與分配的質心之間的總平方距離。K-means是一種可擴展且有效的方法來發現數據中的底層結構，它被廣泛用于分割和模式識別任務。K-means雖然簡單，但對于一些具有復雜結構的數據集可能很困難，因為它對初始聚類質心很敏感，并且假設球形，大小相等的聚類。

K-Means聚類中的假設

在我們深入研究代碼之前，讓我們徹底解釋K-Means聚類的幾個基本假設：

• 球形和各向同性：K-means假設集群是球形和各向同性的，這意味著它們的半徑在所有方向上近似相等。聚類中心被分配給算法根據聚類內數據點的平均值確定的均值。由于這種假設，K-means容易受到非球形或細長聚類的影響。
• 方差相等：所有聚類都被假設為具有相同的方差。這表明對于每個聚類，聚類中心周圍的數據點分布大致相同。如果聚類的方差差異明顯，則K-means可能無法很好地工作。
• 聚類大小：聚類大小相似性由K-means算法假設。具有更多數據點的聚類對聚類均值的影響更大，因為算法會將每個數據點分配給具有最接近均值的聚類。如果聚類的大小嚴重失衡，則算法可能無法正確描述底層數據分布。
• 各向異性分布數據：當K均值聚類中的數據點具有各向異性分布時，它們表示各個維度具有不同擴展的非球形細長聚類。因此，K-means的球形聚類假設被打破，這降低了準確性。對于這種復雜的數據結構，其他技術（如高斯混合模型）可能更合適。

在Scikit Learn中實現k-means假設的演示

導入庫

# immporting Libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobsplt.figure(figsize=(10, 10))# Custom parameters
n_samples_custom = 1600
random_state_custom = 42

合成數據

# Generate blobs with different characteristics
X_custom, y_custom = make_blobs(n_samples=n_samples_custom, random_state=random_state_custom)

這段代碼使用scikit-learn的make_blobs來創建一個包含1600個樣本的合成數據集。然后對數據進行K均值聚類，其中n_clusters=3，聚類以散點圖顯示。為了重現性，參數random_state_custom和n_samples_custom調節數據集的大小和隨機性。

# Incorrect number of clusters
kmeans_1 = KMeans(n_clusters=2, random_state=random_state_custom)
y_pred_custom_1 = kmeans_1.fit_predict(X_custom)plt.subplot(221)
plt.scatter(X_custom[:, 0], X_custom[:, 1], c=y_pred_custom_1)
plt.title("Incorrect Number of Blobs")

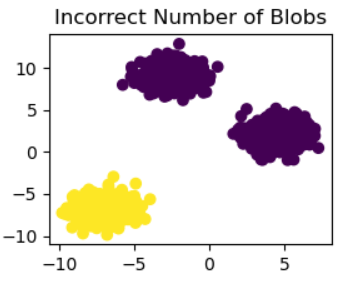
此代碼將n_clusters=2的K-means聚類應用于合成數據集X_custom。接下來，使用plt.scatter，最終的聚類分配（y_pred_custom_1）顯示在散點圖中。“Incorrect Number of Blobs”子圖是由子圖（221）制成的較大圖的一部分。

各向異性地分布簇

# Anisotropicly distributed data
transformation_custom = [[0.5, -0.8], [-0.3, 0.6]]
X_aniso_custom = np.dot(X_custom, transformation_custom)
kmeans_2 = KMeans(n_clusters=3, random_state=random_state_custom)
y_pred_custom_2 = kmeans_2.fit_predict(X_aniso_custom)plt.subplot(222)
plt.scatter(X_aniso_custom[:, 0], X_aniso_custom[:, 1], c=y_pred_custom_2)
plt.title("Anisotropicly Distributed Blobs")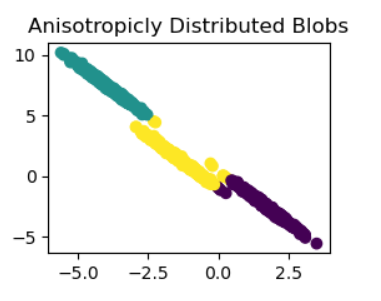

將線性變換（transformation_custom）應用于數據集的原始特征，此代碼將向其添加各向異性。接下來，使用n clusters=3，

K-means對變換后的數據進行聚類（X_aniso_custom）。在名為“Anisotropically Distributed Blobs”的子圖中包含的散點圖中，將顯示最終的聚類指定（y_pred_custom_2）。

不等方差

# Different variance
X_varied_custom, _ = make_blobs(n_samples=n_samples_custom, cluster_std=[1.0, 3.0, 0.5], random_state=random_state_custom)
kmeans_3 = KMeans(n_clusters=3, random_state=random_state_custom)
y_pred_custom_3 = kmeans_3.fit_predict(X_varied_custom)plt.subplot(223)
plt.scatter(X_varied_custom[:, 0], X_varied_custom[:, 1], c=y_pred_custom_3)
plt.title("Unequal Variance")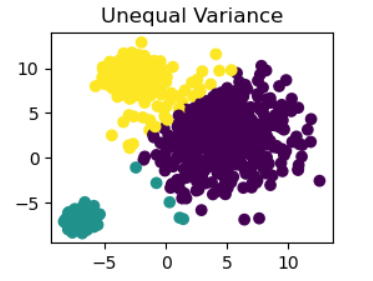

此代碼使用make_blobs函數創建具有不同聚類標準差的數據集（X_varied_custom）。接下來，將n_clusters=3的K均值聚類應用于數據集，并使用標題為“Unequal Variance”的散點圖來可視化聚類分配（y_pred_custom_3）。

大小不一致的blobs

# Unevenly sized blobs
X_filtered_custom = np.vstack((X_custom[y_custom == 0][:500], X_custom[y_custom == 1][:100], X_custom[y_custom == 2][:10]))
kmeans_4 = KMeans(n_clusters=3, random_state=random_state_custom)
y_pred_custom_4 = kmeans_4.fit_predict(X_filtered_custom)plt.subplot(224)
plt.scatter(X_filtered_custom[:, 0],X_filtered_custom[:, 1], c=y_pred_custom_4)
plt.title("Unevenly Sized Blobs")plt.show()

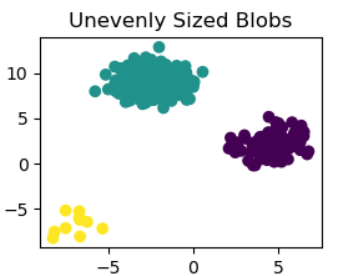
此代碼獲取原始數據集（X_custom），并從每個聚類中選擇不同數量的樣本，以創建大小不均勻的數據集（X_filtered_custom）。修改數據集后，應用n_clusters=3的K-means聚類。然后，在名為“Unevenly sized blobs”的子圖中使用散點圖顯示產生（y_pred_custom_4）的聚類分配。plt.show()顯示完整的圖形。

結論

在Scikit-Learn對K-means假設的演示中，我們系統地研究了算法假設可能被打破的場景。當我們從大小不正確的聚類開始時，首次觀察到K均值對聚類數量的敏感性。各向異性分布的引入突出了K-means在管理非球形聚類方面的局限性，因為該算法默認形成球形聚類。對具有不同方差的聚類的調查突出了K均值在處理不均勻分布的聚類時所面臨的困難。最后，不同大小的blob顯示了算法對集群大小變化的敏感程度。每個場景都顯示了可能的危險，強調理解K-means假設并根據數據集的特征選擇合適的聚類方法是多么重要。更可靠的解決方案可以通過替代技術提供，如高斯混合模型，用于各向異性或大小不均勻的簇等復雜結構。該演示強調了根據數據屬性仔細選擇算法的重要性，并為從業者導航聚類算法的微妙之處提供了有用的見解。