Trie樹：用來高效存儲和查找字符串集合的數據結構：

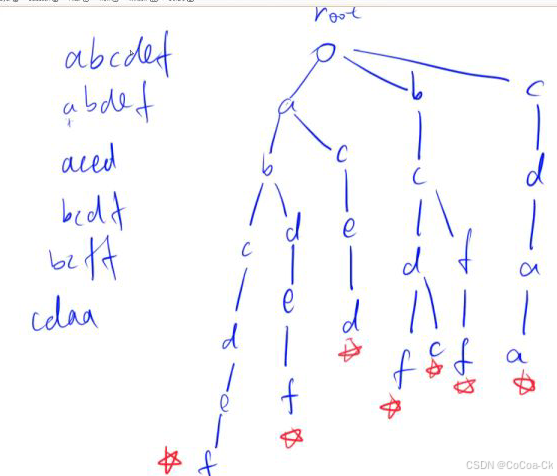
模板題：https://www.acwing.com/problem/content/837/

AC代碼：

#include<bits/stdc++.h>
using namespace std;
int son[100010][26],cnt[100010],idx;
char str[100010];
void insert(char str[])
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';if(!son[p][u]) son[p][u]=++idx;p=son[p][u];}cnt[p]++;
}
int query(char str[])
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';if(!son[p][u]) return 0;p=son[p][u];}return cnt[p];
}
int main()
{int n;cin>>n;while (n -- ){char op[2];scanf("%s%s",op,str);if(op[0]=='I') insert(str);else printf("%d\n",query(str));}
}

再來個十分典的：https://www.acwing.com/problem/content/145/

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
int son[3200000][2],idx,a[100010];
int n;
void insert(int k)
{int p=0;int res=0;for(int i=30;i>=0;i--){int u=k>>i&1;if(!son[p][u]) son[p][u]=++idx;p=son[p][u];}
}
int query(int k)
{int p=0,res=0;for(int i=30;i>=0;i--){int u=k>>i&1;if(!son[p][1-u]){p=son[p][u];res=2*res+u;}else{p=son[p][1-u];res=2*res+1-u;}}return res;
}
int main()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];int res=0;for(int i=1;i<=n;i++){insert(a[i]);int ck=query(a[i]);res=max(res,a[i]^ck);}cout<<res;
}

堆：

主要實現這5個功能：

1.插入一個數 2.求集合最小值 3.刪除最小值 4.刪除任意一個元素 5.修改任意一個元素

是一個完全二叉樹，對于小根堆每一個父節點小于它的兒子，根節點就是min

模板題：https://www.acwing.com/problem/content/840/

AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int h[100010],size1;
void down(int u)
{int t=u;if(u*2<=size1&&h[u*2]<h[t]) t=u*2;if(u*2+1<=size1&&h[u*2+1]<h[t]) t=u*2+1;if(u!=t){swap(h[u],h[t]);down(t);}
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>h[i];size1=n;for(int i=size1/2;i;i--) down(i);while (m -- ){cout<<h[1]<<" ";h[1]=h[size1];size1--;down(1);}
}

模板題：https://www.acwing.com/problem/content/841/

其中用到了映射關系，具體可以看某大佬題解：https://www.acwing.com/solution/content/5661/

AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N=1e5+10;
int h[N];   //堆
int ph[N];  //存放第k個插入點的下標
int hp[N];  //存放堆中點的插入次序
int cur_size;   //size 記錄的是堆當前的數據多少
void heap_swap(int u,int v)
{swap(h[u],h[v]);swap(ph[hp[u]],ph[hp[v]]);swap(hp[u],hp[v]);
}void down(int u)
{int t=u;if(u*2<=cur_size&&h[t]>h[u*2]) t=u*2;if(u*2+1<=cur_size&&h[t]>h[u*2+1])  t=u*2+1;if(u!=t){heap_swap(u,t);down(t);}
}
void up(int u)
{if(u/2>0&&h[u]<h[u/2]) {heap_swap(u,u/2);up(u>>1);}
}
int main()
{int n,m=0;cin>>n;while (n -- ){string op;int k,x;cin>>op;if(op=="I"){cin>>x;m++;h[++cur_size]=x;ph[m]=cur_size;hp[cur_size]=m;up(cur_size);down(cur_size);}else if(op=="PM")    cout<<h[1]<<endl;else if(op=="DM"){heap_swap(1,cur_size);cur_size--;down(1);}else if(op=="D"){cin>>k;int u=ph[k];//注意不能直接ph[k]heap_swap(ph[k],cur_size);cur_size--;down(u);up(u);}else if(op=="C"){cin>>k>>x;h[ph[k]]=x;                 down(ph[k]);                up(ph[k]);}}
}

哈希表：按照存儲結構可以分為開放尋址法以及拉鏈法

模板題：https://www.acwing.com/problem/content/842/

拉鏈法的AC代碼：

#include<bits/stdc++.h>
using namespace std;
const int N=100003,null=0x3f3f3f3f;//最好是質數
int h[N],e[N],ne[N],idx;//鏈表,h相當于槽,類似鏈式前向星
void insert(int x){int k=(x%N+N)%N;e[idx]=x,ne[idx]=h[k],h[k]=idx++;}
bool find(int x){int k=(x%N+N)%N;for(int i=h[k];i!=-1;i=ne[i]){if(e[i]==x) return 1;}return 0;
}
int main(){int n;cin>>n;memset(h,-1,sizeof(h));while(n--){char op[2];int x;scanf("%s%d",op,&x);if(*op=='I') insert(x);else{if(find(x)) puts("Yes");else puts("No");}}
}

開放尋址法：

#include<bits/stdc++.h>
using namespace std;
const int M=200003,null=0x3f3f3f3f;
int h[M];
int find(int x){int k=(x%M+M)%M;while(h[k]!=null&&h[k]!=x){k++;if(k==M) k=0;}return k;
}
int main(){int n;cin>>n;memset(h,0x3f,sizeof(h));while(n--){char op[2];int x;scanf("%s%d",op,&x);if(*op=='I'){int k=find(x);h[k]=x;}else{int k=find(x);if(h[k]!=null) puts("Yes");else puts("No");}}
}

還可以通過字符串前綴哈希法：https://www.acwing.com/activity/content/problem/content/891/

具體就是先確定一個把字符串映射成一個數的函數，我們可以把它看出p進制再mod Q，A,B,等賦予不同的權值（最好不要0，否則AA,A就是同一個了），這里有個經驗值，我們一般取p=131或者13331,Q=2^64,我們可以認為此時沒有沖突值。

這樣+前綴哈希就可以計算出所有子串的哈希值：h[r]-h[l]*p^(r-l+1).

這里有個技巧：我們開unsigned long long 這樣modQ就可以用溢出直接代替了?

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N = 100010, P = 131;int n, m;
char str[N];
ull h[N], p[N];
ull get(int l, int r)
{return h[r] - h[l - 1] * p[r - l + 1];
}
int main()
{scanf("%d%d", &n, &m);scanf("%s", str + 1);p[0]=1;for(int i=1;i<=n;i++){h[i] = h[i - 1] * P + str[i];p[i] = p[i - 1] * P;}while (m -- ){int l1, r1, l2, r2;scanf("%d%d%d%d", &l1, &r1, &l2, &r2);if (get(l1, r1) == get(l2, r2)) puts("Yes");else puts("No");}
}