【matlab 路徑規劃】基于改進遺傳粒子群算法的藥店配送路徑優化

一背景介紹

本文分享的是一個基于訂單合并的訂單分配和路徑規劃聯合優化，主要背景是騎手根據客戶需求，從藥店取藥之后進行配送，配送的過程中考慮路徑的長度、客戶的服務時間窗、車輛的固定成本等要素，經過建模和優化得到最優的配送方案。

二模型介紹

2.1基本假設

配送的具體流程和現實情況,建立的數學模型基于以下假設條件:
(1)O2O 藥品零售平臺旗下的各個門店能夠滿足已下單顧客的需求量，即不存在供不應
求的情況。
(2)已知消費者下單商品數量、地理位置及時間窗和每個消費者的需求量不會發生變化
(3)騎手在每個配送點服務時間恒定且相同，由于服務時間較短所以忽略不計。
(4)騎手從藥店出發，中途不可返回藥店取貨，完成所有的配送任務后需要返回藥店。
(5)在騎手對各配送點進行配送的過程中，不考慮交通堵塞、車輛故障、天氣惡劣等突
發狀況的影響。

2.2目標函數

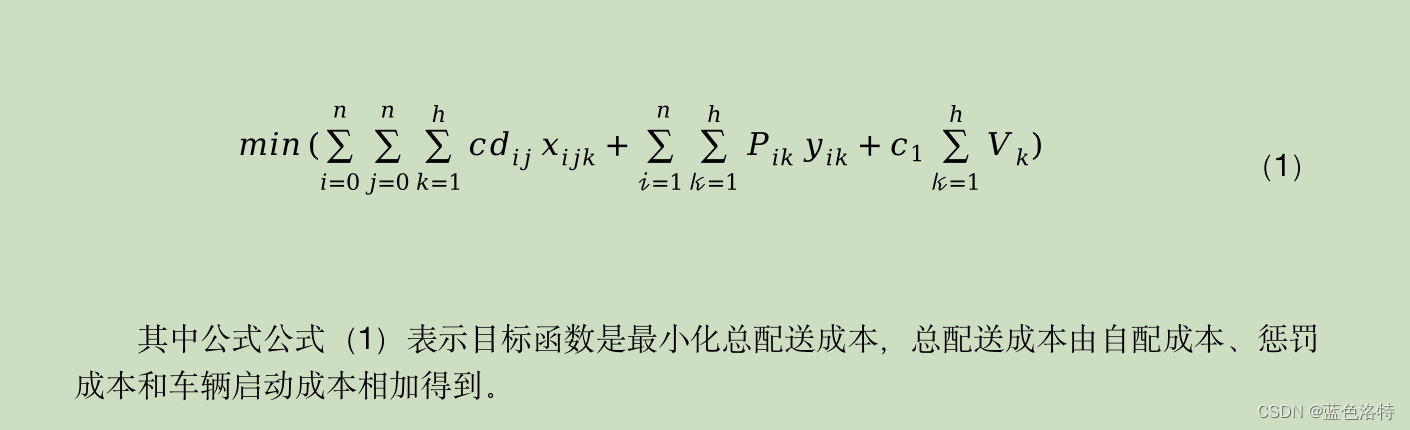
在這里插入圖片描述

2.3 約束條件

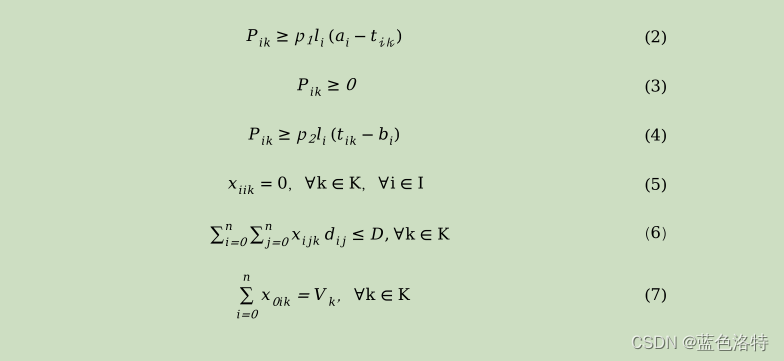
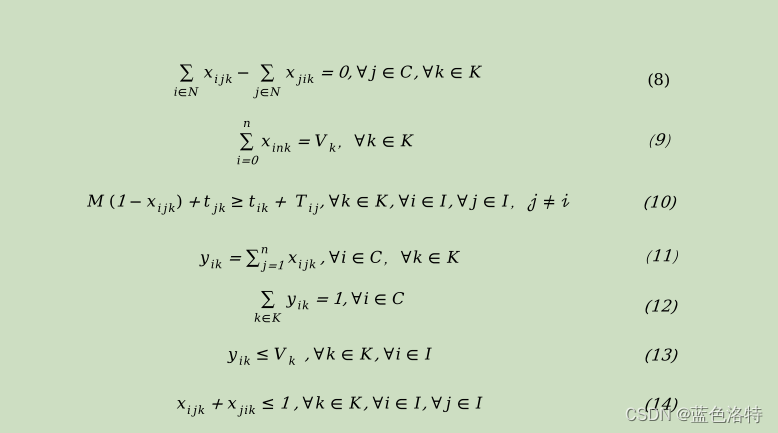
在這里插入圖片描述

三算法介紹

遺傳算法是一種模擬自然進化過程的優化算法，用于解決優化問題。它模擬了生物進化的過程，通過對優良個體的選擇、交叉和變異，逐步優化解的質量，最終找到最優解。

遺傳算法的基本步驟包括：

初始化種群：隨機生成一組初始解作為種群，通常采用隨機數生成的方式。

適應度評價：根據問題的具體要求，采用適應度函數對每個個體進行評估，得到其適應度值。

選擇操作：根據個體的適應度值，按照一定的選擇概率選擇優良個體作為父代，通常采用輪盤賭選擇方法。

交叉操作：從選出的父代個體中選取一對個體，通過某種交叉方式生成新的個體。

變異操作：對新生成的個體進行一定的變異操作，改變其基因的值，增加種群的多樣性。

更新種群：將新生成的個體加入到種群中，得到更新后的種群。

終止條件判斷：判斷是否滿足終止條件，如達到最大迭代次數或找到滿足要求的解。

返回最優解：返回種群中適應度最好的個體作為最優解。

遺傳算法通過迭代優化的方式，不斷改進解的質量，尋找到全局最優解或較好的局部最優解。它在解決復雜問題、搜索空間大的問題等方面具有很好的性能。

四算例分析

算例1 本文使用30個節點的算例，1個配送節點 29個需求節點（分為三個優先級）
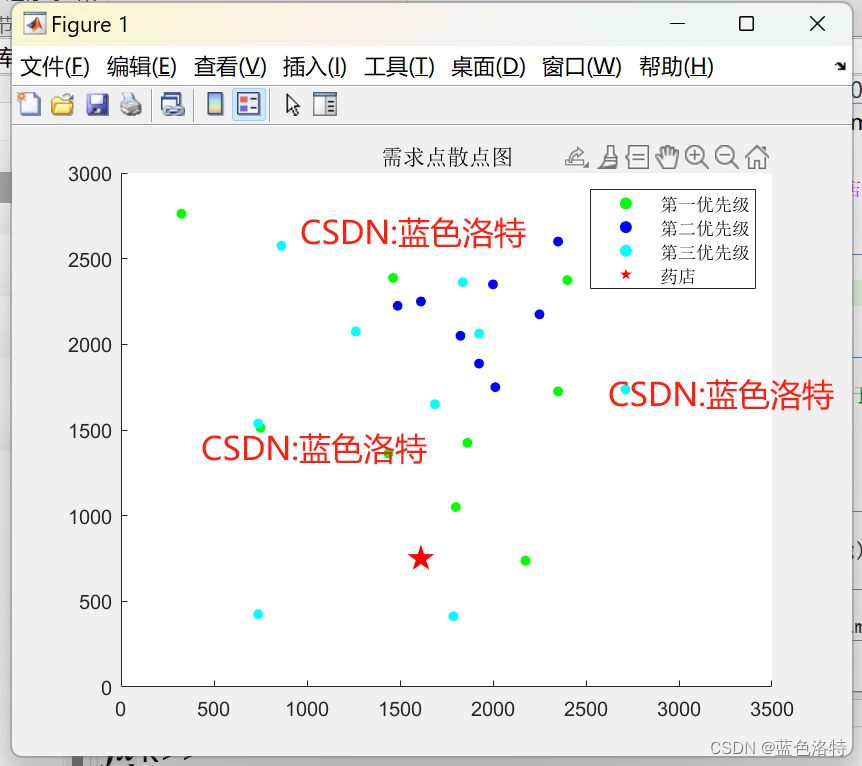
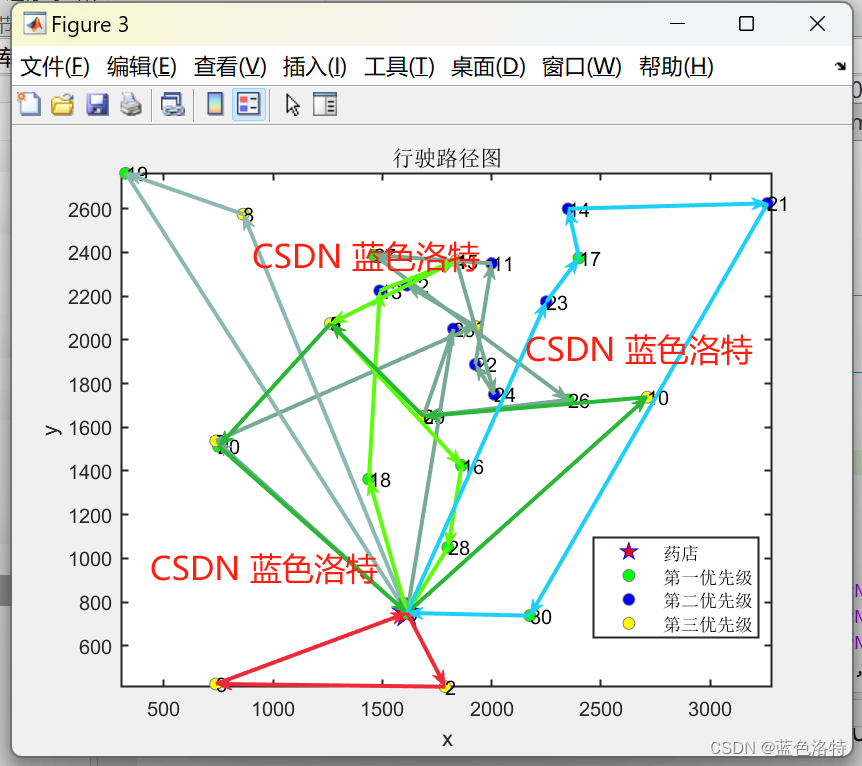
在這里插入圖片描述

車輛編號.1: 0 -> 7 -> 1 -> 12 -> 15 -> 24 -> 22 -> 11 -> 27 -> 26 -> 29 ->
25 -> 0 到達時間節點: 0 - 4.7 - 9.9 - 11.4 - 12.4 - 14.9 - 15.6 - 17.4 -
19.6 - 24 - 26.7 - 28.4 - 33.7 min 行駛距離: 8413.36 m, 總時間: 33.7 min; 行駛成本 (C1): 21.03, 懲罰成本 (C2): 50.88
------------------------------------------------------------- 車輛編號.2: 0 -> 8 -> 19 -> 0 到達時間節點: 0 - 7.9 - 10.2 - 19.7 min 行駛距離: 4931.47
m, 總時間: 19.7 min; 行駛成本 (C1): 12.33, 懲罰成本 (C2): 29.59
------------------------------------------------------------- 車輛編號.3: 0 -> 18 -> 13 -> 4 -> 5 -> 16 -> 28 -> 0 到達時間節點: 0 - 2.5 - 6 - 7.5 -
10.1 - 13.6 - 15.1 - 16.6 min 行駛距離: 4138.40 m, 總時間: 16.6 min; 行駛成本 (C1): 10.35, 懲罰成本 (C2): 29.81
------------------------------------------------------------- 車輛編號.4: 0 -> 10 -> 6 -> 9 -> 20 -> 0 到達時間節點: 0 - 5.9 - 10 - 12.4 - 15.5 -
20.1 min 行駛距離: 5020.18 m, 總時間: 20.1 min; 行駛成本 (C1): 12.55, 懲罰成本 (C2): 33.81
------------------------------------------------------------- 車輛編號.5: 0 -> 23 -> 17 -> 14 -> 21 -> 30 -> 0 到達時間節點: 0 - 6.2 - 7.2 - 8.2 -
11.8 - 20.5 - 22.8 min 行駛距離: 5695.44 m, 總時間: 22.8 min; 行駛成本 (C1): 14.24, 懲罰成本 (C2): 37.93
------------------------------------------------------------- 車輛編號.6: 0 -> 2 -> 3 -> 0 到達時間節點: 0 - 1.5 - 5.7 - 9.5 min 行駛距離: 2363.65 m,
總時間: 9.5 min; 行駛成本 (C1): 5.91, 懲罰成本 (C2): 14.18

算例2 本文使用10個節點的算例，1個配送節點 9個需求節點（分為三個優先級）

在這里插入圖片描述
**

車輛編號.1: 0 -> 2 -> 3 -> 1 -> 5 -> 4 -> 7 -> 8 -> 9 -> 6 -> 0 到達時間節點:
0 - 1.5 - 5.7 - 13.8 - 15.3 - 16.9 - 18.5 - 22.1 - 27.2 - 29.5 - 32.4
min 行駛距離: 8090.30 m, 總時間: 32.4 min; 行駛成本 (C1): 20.23, 懲罰成本 (C2):
54.26

六項目分享

部分源碼

clc
clear
close all
tic % 保存當前時間dataloader
%% 初始化問題參數
CustomerNum = size(Position, 1) - 1; % 需求點個數%% 需求點繪圖
figure
hold on
xx = Position(:, 1);
yy = Position(:, 2);
idx1 = find(order_priority == 1);
idx2 = find(order_priority == 2);
idx3 = find(order_priority == 3);
scatter(xx(idx1), yy(idx1), 25, 'filled', 'go', 'DisplayName', '第一優先級')
scatter(xx(idx2), yy(idx2), 25, 'filled', 'bo', 'DisplayName', '第二優先級')
scatter(xx(idx3), yy(idx3), 25, 'filled', 'yo', 'DisplayName', '第三優先級')
scatter(xx(1), yy(1), 200, 'filled', 'rp', 'DisplayName', '藥店')
legend
title('需求點散點圖')%% 初始化算法參數
NIND = 1000; % 粒子數量
MAXGEN = 100; % 最大迭代次數
mutation_prob = 0.05; % 變異概率
crossover_prob = 0.8; % 交叉概率
tournament_size = 5; % 錦標賽規模%% 為預分配內存而初始化的0矩陣
Population = zeros(NIND, CustomerNum * 2 + 1); % 預分配內存，用于存儲種群數據
PopDistance = zeros(NIND, 1); % 預分配矩陣內存
GbestDisByGen = zeros(MAXGEN, 1); % 預分配矩陣內存penalty_costs = zeros(NIND, 1);
travel_costs = zeros(NIND, 1);
vehicle_costs = zeros(NIND, 1);
total_distances = zeros(NIND, 1);
penalty_orders = cell(NIND, 1);for i = 1:NIND%% 初始化各粒子Population(i, :) = InitPop(CustomerNum, Distance, setting); % 使用GRASP算法生成TSP路徑%% 計算路徑長度PopDistance(i) = CalcDis(Population(i,:),Distance,TimeWindow,order_priority,setting); % 計算路徑長度
end
%% 存儲Pbest數據
Pbest = Population; % 初始化Pbest為當前粒子集合
PbestDistance = PopDistance; % 初始化Pbest的目標函數值為當前粒子集合的目標函數值%% 存儲Gbest數據
[mindis, index] = min(PbestDistance); % 獲得Pbest中
Gbest = Pbest(index, :); % 初始Gbest粒子
GbestDistance = mindis; % 初始Gbest粒子的目標函數值%% 開始迭代
gen = 1;while gen <= MAXGEN%% 選擇算子（錦標賽選擇）new_population = zeros(size(Population));for i = 1:NINDnew_population(i, :) = Selection(Population, PopDistance, tournament_size); % 錦標賽選擇endPopulation = new_population;%% 每個粒子更新for i = 1:NIND%% 粒子與Pbest交叉if rand < crossover_probPopulation(i, 2:end-1) = Crossover(Population(i, 2:end-1), Pbest(i, 2:end-1)); % 交叉end% 新路徑長度變短則記錄至PbestPopDistance(i) = CalcDis(Population(i,:),Distance,TimeWindow,order_priority,setting); % 計算路徑長度if PopDistance(i) < PbestDistance(i) % 若新路徑長度變短Pbest(i, :) = Population(i, :); % 更新PbestPbestDistance(i) = PopDistance(i); % 更新Pbest距離end%% 根據Pbest更新Gbest[mindis, index] = min(PbestDistance); % 找出Pbest中最短距離if mindis < GbestDistance % 若Pbest中最短距離小于Gbest距離Gbest = Pbest(index, :); % 更新GbestGbestDistance = mindis; % 更新Gbest距離end%% 粒子與Gbest交叉if rand < crossover_probPopulation(i, 2:end-1) = Crossover(Population(i, 2:end-1), Gbest(2:end-1));end% 新路徑長度變短則記錄至PbestPopDistance(i) = CalcDis(Population(i,:),Distance,TimeWindow,order_priority,setting); % 計算路徑長度if PopDistance(i) < PbestDistance(i) % 若新路徑長度變短Pbest(i, :) = Population(i, :); % 更新PbestPbestDistance(i) = PopDistance(i); % 更新Pbest距離end%% 粒子自身變異if rand < mutation_probPopulation(i, :) = Mutate(Population(i, :), Distance); % 傳遞Distance矩陣end% 新路徑長度變短則記錄至PbestPopDistance(i) = CalcDis(Population(i,:),Distance,TimeWindow,order_priority,setting); % 計算路徑長度if PopDistance(i) < PbestDistance(i) % 若新路徑長度變短Pbest(i, :) = Population(i, :); % 更新PbestPbestDistance(i) = PopDistance(i); % 更新Pbest距離end%% 根據Pbest更新Gbest[mindis, index] = min(PbestDistance); % 找出Pbest中最短距離if mindis < GbestDistance % 若Pbest中最短距離小于Gbest距離Gbest = Pbest(index, :); % 更新GbestGbestDistance = mindis; % 更新Gbest距離endend%% 顯示此代信息fprintf('迭代次數 = %d, 最小成本 = %.2f   \n', gen, GbestDistance)%% 存儲此代最短距離GbestDisByGen(gen) = GbestDistance;%% 更新迭代次數gen = gen + 1;
end% 刪去路徑中多余1
for i = 1:length(Gbest) - 1if Gbest(i) == Gbest(i + 1)Gbest(i) = 0; % 相鄰位都為1時前一個置零end
end
Gbest(Gbest == 0) = []; % 刪去多余零元素Gbest = Gbest - 1; % 編碼各減1，與文中的編碼一致%% 計算結果數據輸出到命令行
disp('-------------------------------------------------------------')
toc % 顯示運行時間
TextOutput(Gbest, Distance, TimeWindow, setting); % 顯示最優路徑
disp('-------------------------------------------------------------')%% 迭代圖
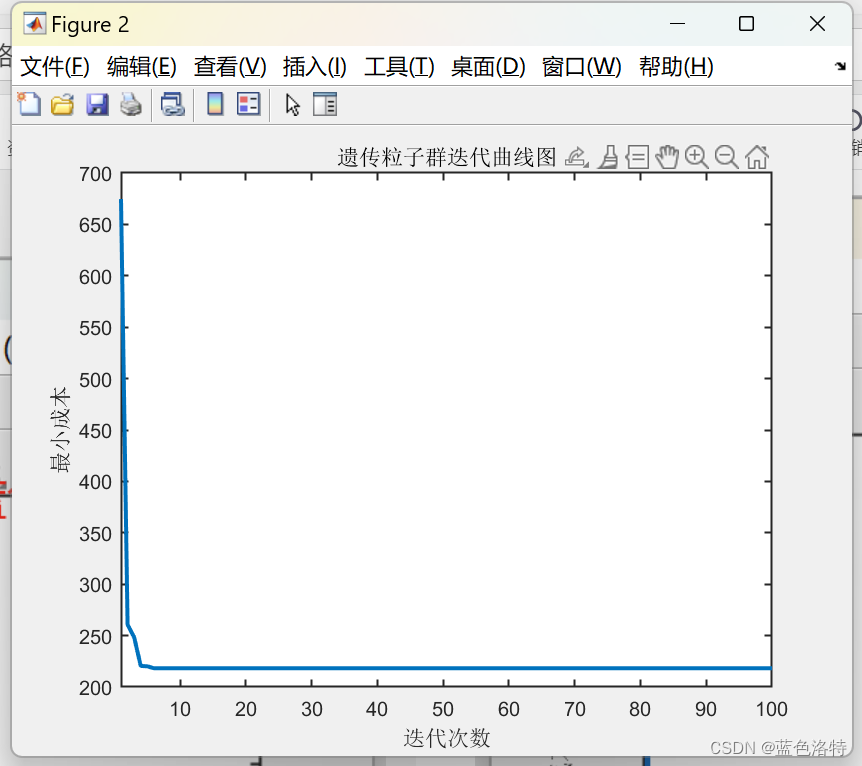
figure
plot(GbestDisByGen, 'LineWidth', 2) % 展示目標函數值歷史變化
xlim([1 gen - 1]) % 設置 x 坐標軸范圍
set(gca, 'LineWidth', 1)
xlabel('迭代次數')
ylabel('最小成本')
title('遺傳粒子群迭代曲線圖')%% 繪制實際路線
DrawPath(Gbest, Position, idx1, idx2, idx3)