關鍵路徑，是項目網絡中從起始事件到終止事件的最長路徑，決定了項目的最短完成時間。

關鍵路徑中的任務沒有任何可調整的余地，如果任何一個任務被延遲，整個項目的完成時間也會被延遲。

假設我們現在有一個圖：把圖的邊看作是活動，權值為活動的持續時間；圖的頂點看作是事件，事件是指在項目中發生的關鍵時間點沒有時間，即箭頭的頭是事件開始，箭頭末尾是事件完成。這就是所謂的AOE圖

在以前我們把邊看作是距離，在這里我們把邊看作是時間，即頂點到頂點所需的時間，那么接下來我們就要引出幾個概念：

事件的最早開始時間和最晚開始時間

????????我們假設頂點0是從時間為0時開始的，那么頂點1的最早開始時間為 6（因為需要經過時間為6的活動），頂點 2 為 4 ，頂點 3 為 5 。那么頂點 4 的最早起始時間是什么時候？因為要等活動全部進行完才可以進行下一個活動，所以頂點 4 的最早起始時間為 7，同樣對于頂點 8 來說，有多條路徑，但是要等前面所有活動都進行完，也就是取時間最長的，所以是（7+9+2）或者（7+7+4）路徑而不是走頂點0，3，5，7，這樣加起來是17<18。

所以事件（頂點）的最早開始時間為（從0到8）：

0，6，4，5，7，7，16，14，18

????????接下來是最晚開始時間，最晚時間代表著在不延誤項目的情況下，最晚開始的時間。對于最后的事件 8 ，最晚開始時間就是最早開始時間（意思就是后面沒得可以做了，要立刻宣布項目的完成，所以最晚也是最早），所以事件 8 的最晚開始時間為 18。

????????反推前面的事件，事件 6 的最晚開始時間為 18-2=16，事件 7 的最晚開始時間為 18-4=14，事件 5 的最晚開始時間為 14-4=10，事件 4 的最晚開始時間為 16-9=7 或者 14-7=7，事件 3 的最晚開始時間為 10-2=8，事件 2 和事件 1 的最晚開始事件為7-1=6，那么事件0的最晚開始時間為多少？是6-6=0，6-4=2，還是8-5=3？考慮到不能延誤活動，應該是三個中最小的6-6=0。

所以事件的最晚開始時間為（從0到8）：

0，6，6，8，7，10，16，14，18

當事件的最早開始時間和最晚開始時間相等時叫做關鍵事件，這代表著此事件是項目的關鍵項目，不可拖延。

活動的最早開始事件和最晚開始事件

????????對于活動來說，最早開始時間就是箭頭起始事件的最早開始時間，意味著這時已經可以開始進行活動了，所以對于ABC活動來說，最早開始時間都是0，D為6，E為4，F為5，那么GH的最早開始時間是多少?這里GH是事件4的最早開始事件，為7，以此類推。

最后，活動的最早開始時間，從（A到K）：

0，0，0，6，4，5，7，7，7，16，14

????????最晚開始時間是箭頭的終止事件的最晚開始時間減去權值，意味著這時必須要開始進行活動了，否則會延誤，對于A來說，事件1的最晚開始時間為6，所以6-6=0，B，事件2的最晚開始時間為6，6-4=2，也就是說，B活動最晚要在時間為 2 的時候進行。以此類推。

最后，活動的最晚開始時間，從（A到K）：

0，2，3，6，6，8，7，7，10，16，14

講完這兩個概念，才到文章的主題：關鍵路徑。

????????關鍵路徑是指活動的最早開始時間減去最晚開始時間為0的活動，也就是沒有時間余量。我們可以發現 ADGHJK 活動是最早開始時間等于最晚開始時間的，所以這就是關鍵路徑，如圖：

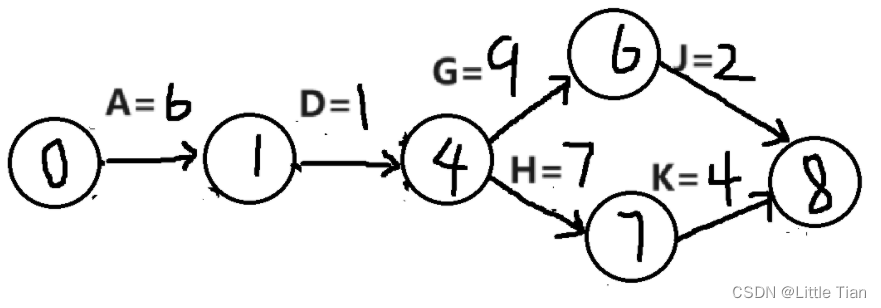????????因為關鍵路徑是最短完成項目的事件，所以在優化項目的時候要著重優化這幾個活動，從而提高效率，這就是關鍵路徑的意義。

現在我們可以先思考一下代碼的過程：

1.拓撲排序，因為最早最晚時間要考慮前驅后繼（事件）

2.計算事件的最早最晚時間，根據是否相等確定關鍵路徑上的事件。

3.找出關鍵路徑

完整的代碼會在下一篇文章，希望對你有所幫助，如有錯誤歡迎指出。