目錄
- 1.下降路徑最小和
- 1.題目鏈接
- 2.算法原理詳解
- 3.代碼實現
- 2.最小路徑和
- 1.題目鏈接
- 2.算法原理詳解
- 3.代碼實現
- 3.地下城游戲
- 1.題目鏈接
- 2.算法原理詳解
- 3.代碼實現
1.下降路徑最小和
1.題目鏈接
- 下降路徑最小和
2.算法原理詳解
- 思路:
-
確定狀態表示 ->
dp[i][j]的含義- 到達
[i, j]位置時,最小的下降路徑
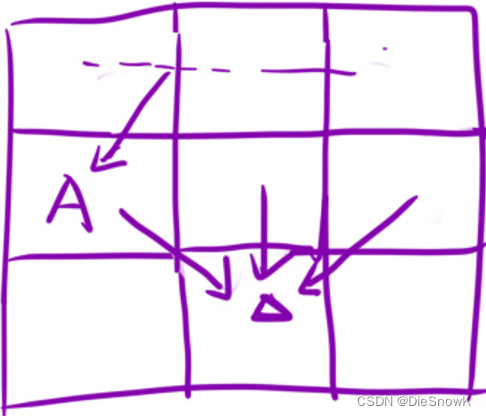
- 到達
-
推導狀態轉移方程
dp[i][j] = min(x, y, z) + m[i][j]
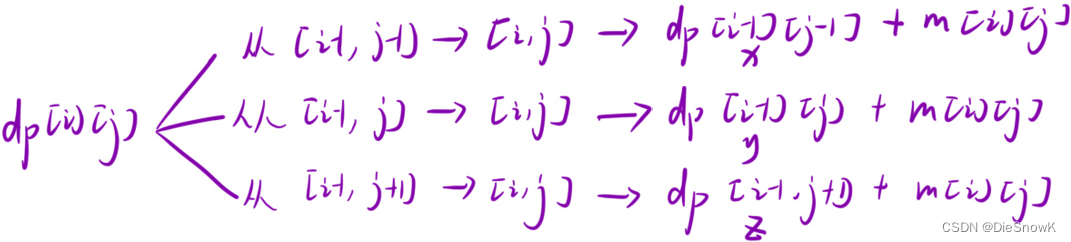
-
初始化:
vector<vector<int>> dp(n + 1, vector<int>(m + 2, INT_MAX))dp[0, i] = 0-> 第一行初始化為0
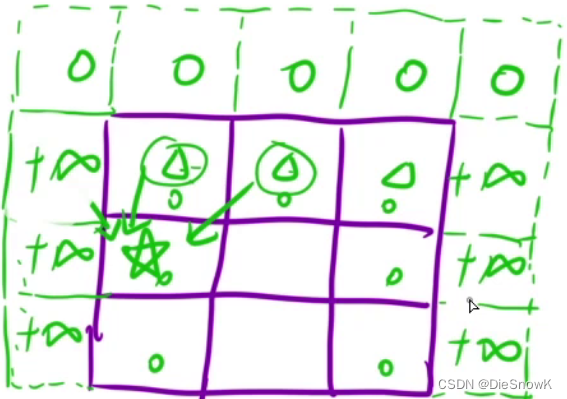
-
確定填表順序:從上往下
-
確定返回值:最后一行的最小值
-
3.代碼實現
int minFallingPathSum(vector<vector<int>>& matrix)
{// Initint n = matrix.size();vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));for(int i = 0; i < n + 2; i++){dp[0][i] = 0;}// Dynamic Planfor(int i = 1; i < n + 1; i++){for(int j = 1; j < n + 1; j++){dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1]))+ matrix[i - 1][j - 1]; }}// 找最小值int ret = INT_MAX;for(int i = 0; i < n + 2; i++){ret = min(ret, dp[n][i]);}return ret;
}
2.最小路徑和
1.題目鏈接
- 最小路徑和
2.算法原理詳解
- 思路:
-
確定狀態表示 ->
dp[i][j]的含義- 走到
dp[i][j]的時候,最小路徑和
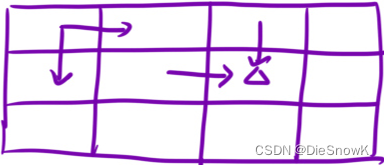
- 走到
-
推導狀態轉移方程
dp[i][j] = min(dp[i - 1][j] + dp[i][j - 1]) + g[i - 1][j - 1]
-
初始化:
dp表多開一行和一列虛擬結點,避免處理邊界dp[0][1] = dp[1][0] = 0
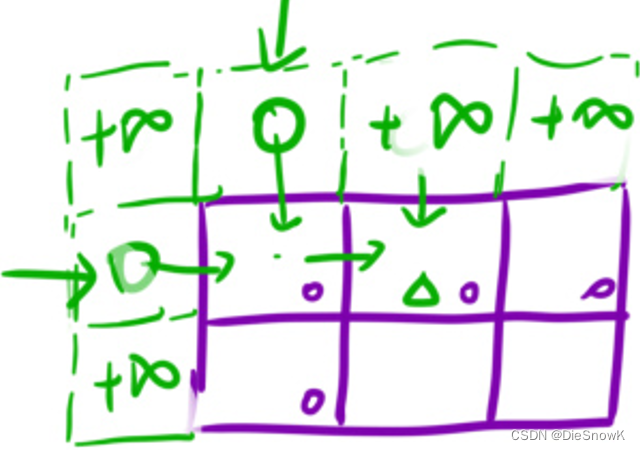
-
確定填表順序:從上往下,從左往右
-
確定返回值:
dp[n][m]
-
3.代碼實現
int minPathSum(vector<vector<int>>& grid)
{// Initint n = grid.size(), m = grid[0].size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX));dp[0][1] = dp[1][0] = 0;// Dynamic Planfor(int i = 1; i < n + 1; i++){for(int j = 1; j < m + 1; j++){dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[n][m];
}
3.地下城游戲
1.題目鏈接
- 地下城游戲
2.算法原理詳解
- 思路:
-
確定狀態表示 ->
dp[i][j]的含義- 從
[i, j]出發,到達終點,所需的最低初始健康點數
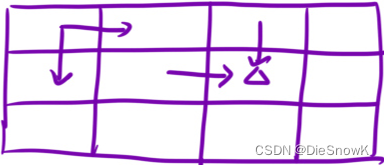
- 從
-
推導狀態轉移方程
dp[i][j] = min(dp[i][j + 1] + dp[i + 1][j]) - d[i][j]dp[i][j] = max(1, dp[i][j]- 避免出現負血量也可以來到此位置
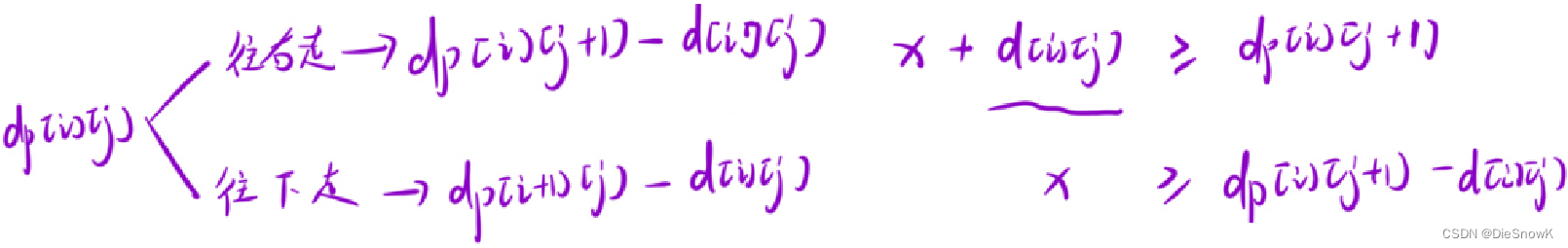
- 避免出現負血量也可以來到此位置
-
初始化:
vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX))dp[n][m - 1] = dp[n - 1][m] = 1
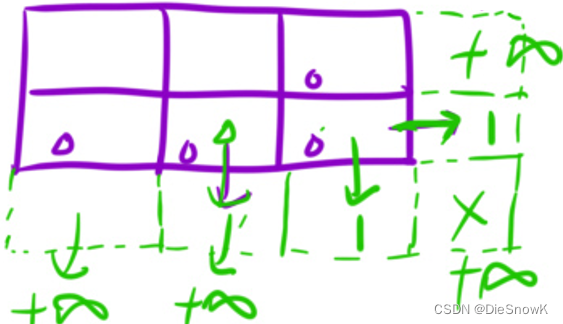
-
確定填表順序:從下往上,從右往左
-
確定返回值:
dp[0][0]
-
- 本題為什么不可以到
[i, j]…?- 因為本題中,
[i, j]的值不僅受前面兩個值影響,也受后面兩個值影響 - 如果從前面,可能確實從前面可以到
[i, j],但是從[i, j]到后面就無法進行下去了
- 因為本題中,
3.代碼實現
int calculateMinimumHP(vector<vector<int>>& d)
{// Initint n = d.size(), m = d[0].size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX));dp[n][m - 1] = dp[n - 1][m] = 1;// Dynamic Planfor(int i = n - 1; i >= 0; i--){for(int j = m - 1; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - d[i][j];dp[i][j] = max(1, dp[i][j]); // 防止"死了還能到":P}}return dp[0][0];
}












之內嵌容器)
——國際化)
)
-滑動窗口最大值 + 前 K 個高頻元素 + 總結)
)


