本篇會加入個人的所謂魚式瘋言

??????魚式瘋言:??????此瘋言非彼瘋言

而是理解過并總結出來通俗易懂的大白話,

小編會盡可能的在每個概念后插入魚式瘋言,幫助大家理解的.

🤭🤭🤭可能說的不是那么嚴謹.但小編初心是能讓更多人能接受我們這個概念 ！！！

前言

在前面的章節中，我們學習了 "雙指針"算法 ， “滑動窗口"算法

而在本篇章節 ， 我們期待已久的 “二分查找”算法 即將登場， 透露下本次算法主要的規劃 💖 💖 💖

目錄

1. 二分算法的初識

2. 二分算法的應用

3. 二分算法的總結

一. 二分算法的初識

1. 二分算法的簡介

二分算法，也被稱為 二分查找 算法，是一種常用的查找 算法。

它的基本思想是將已排序的數據序列分成 兩部分 ，取中間 的元素與 目標值 進行比較，然后根據比較結果，確定目標值 在左半部分還是 右半部分，再繼續在相應的部分進行 查找，直到找到目標值或者確定目標值 不存在 為止。

2. 二分算法的使用步驟

因為二分查找算法分為兩種：

“一種是 樸素二分查找” 算法， 另外一種是 "左右邊界二分查找 " 算法

因為樸素二分查找比較基礎，我們先學習基礎版本的，再調整有難度的 💖 💖 💖

小編在這里說明 “樸素二分查找” 的具體步驟哦

先拿個題目來瞧瞧唄

二分查找

704.二分查找題目鏈接

<1>. 題目描述

給定一個 n 個元素有序的（升序）整型數組 nums 和一個目標值 target ，寫一個函數搜索 nums 中的 target，如果目標值存在返回下標，否則返回 -1。

示例 1:

輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中并且下標為 4

示例 2:

輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

題目含義

在給定的數組中查找一個數 ，返回其 下標 ，如果沒有就返回 -1

<2>. 講解算法思想

題目分析 ： 我們要查找一個數最簡單的方式

解法一 ：

暴力求解

用一個 for -遍歷 數組 ，然后中間用一個 if 來判斷 ，一定成立就返回其下標

在解法一的基礎上，我們為了減少一半的數據，特別提煉出 二分查找 算法的思想

解法二 ：

二分算法 :

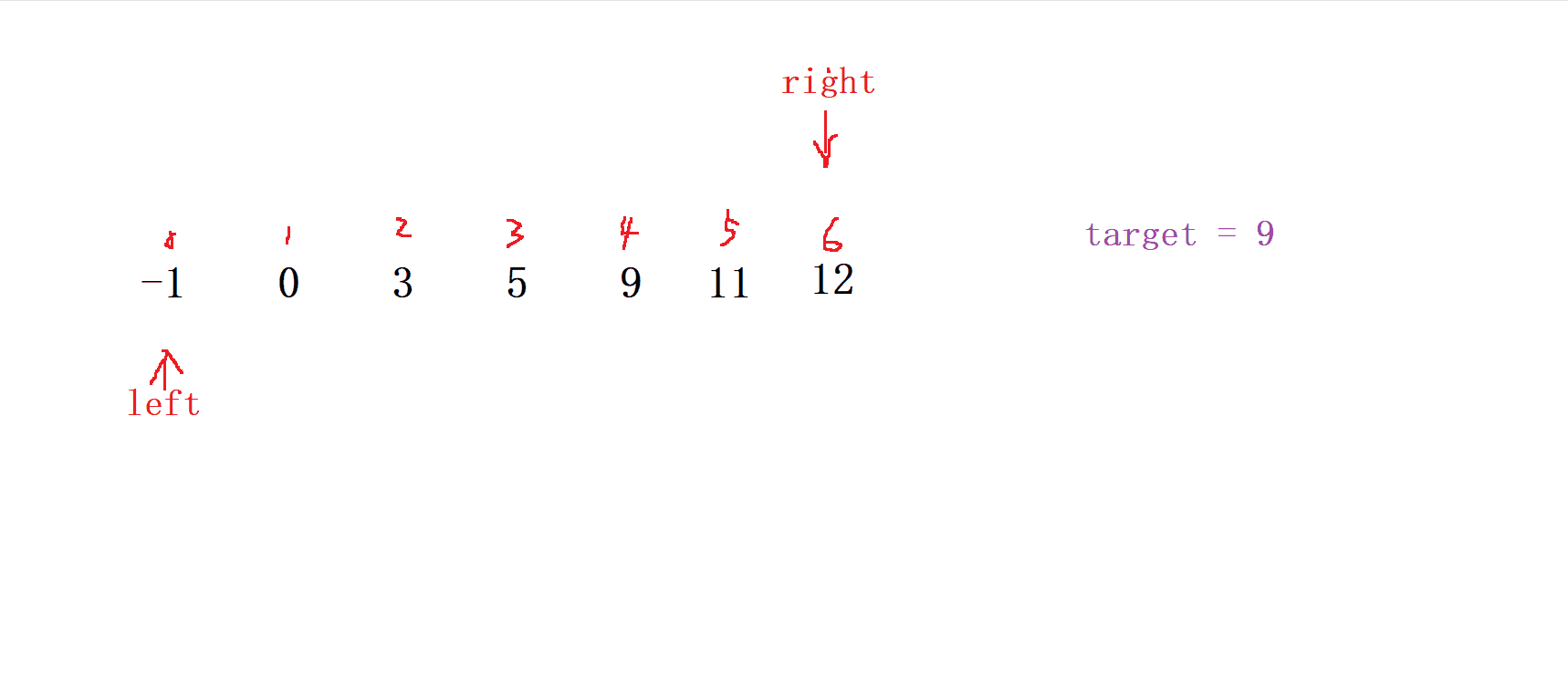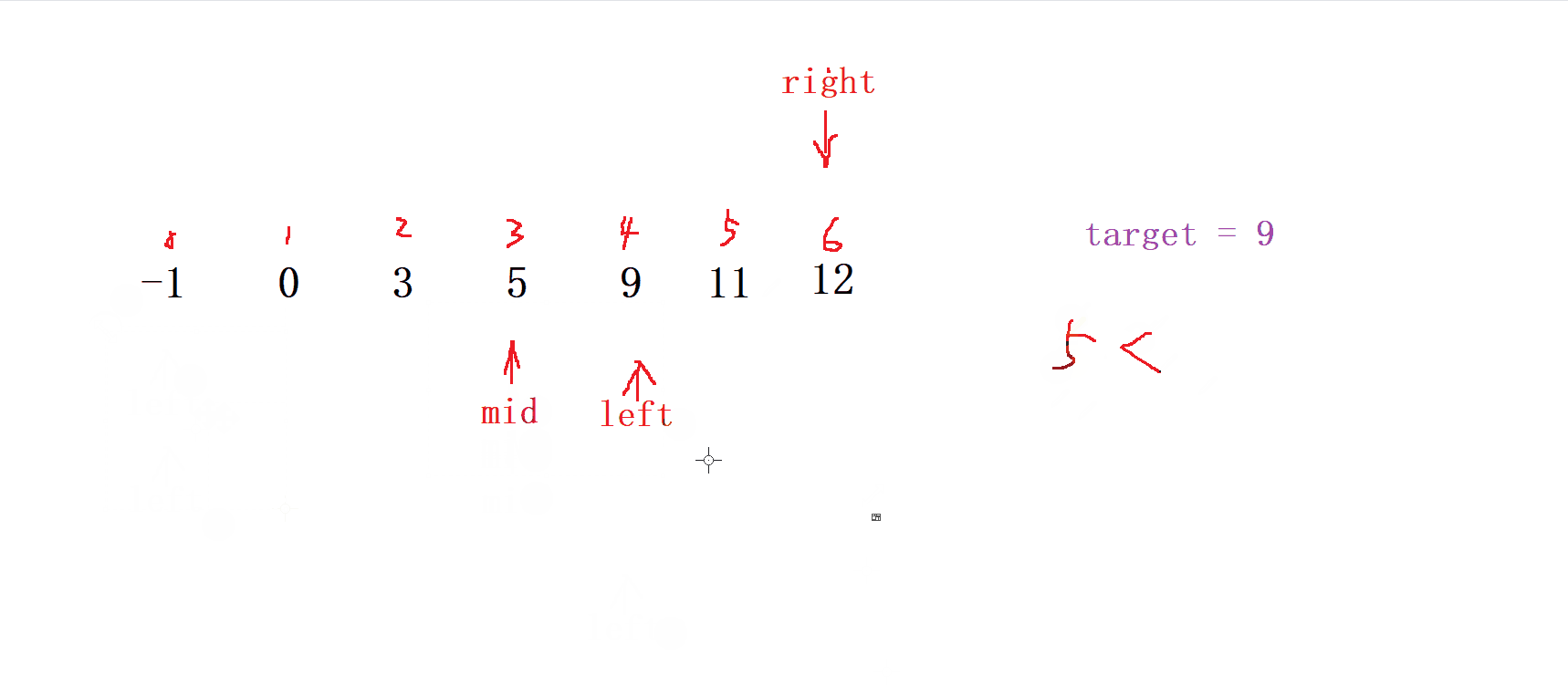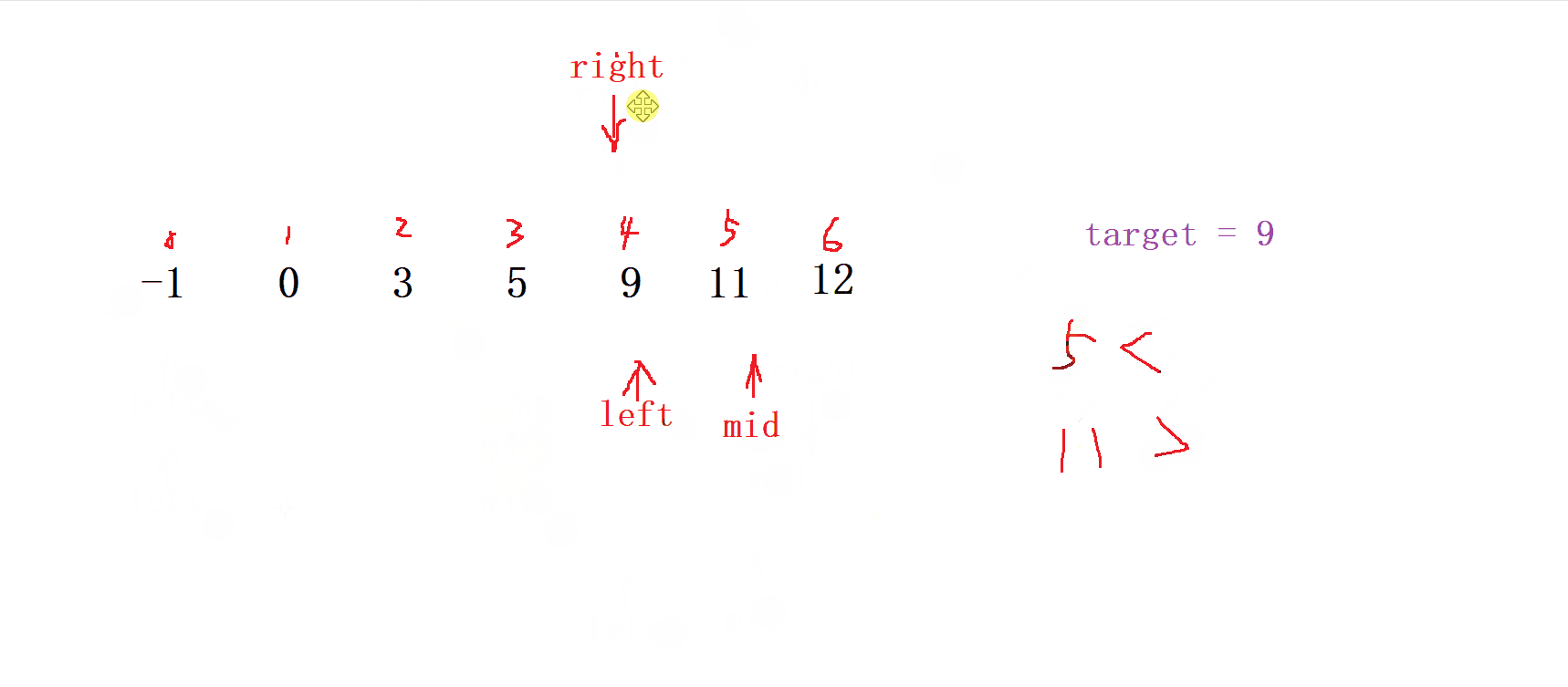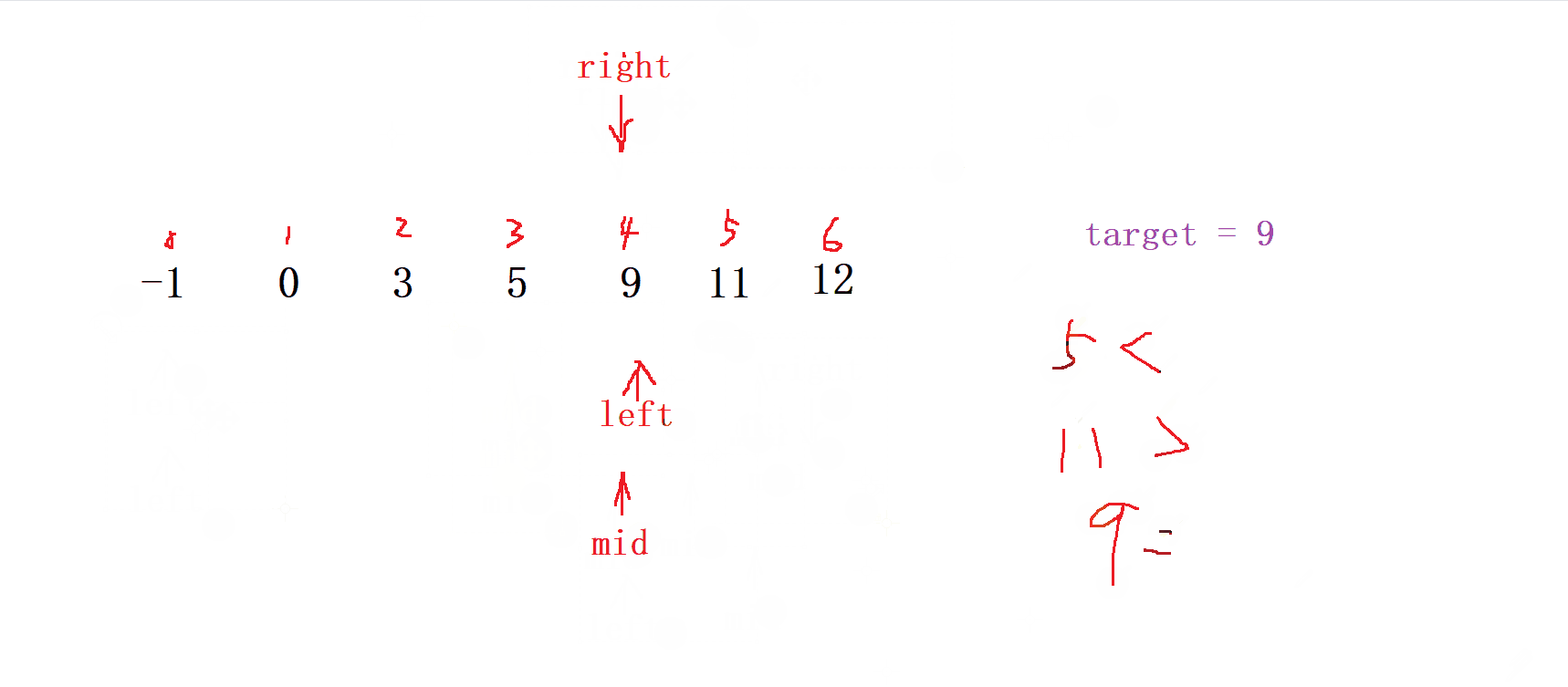
• 首先，確定要查找的目標值在序列中的可能范圍，通常是通過比較目標值和序列的 第一個元素 和 最后一個元素 來確定；

我們定義 一個數組的第一個元素的為 left ， 再定義 最后一個元素 的下標為 right

• 然后，在可能范圍內，取中間的元素與目標值進行比較；

• 如果中間的元素等于目標值，則查找成功，返回對應的位置；

• 如果中間的元素 大于 目標值，則說明目標值可能在 左半部分 ，縮小范圍到 左半部分 繼續查找，重復步驟2；

• 如果中間的元素 小于 目標值，則說明目標值可能在 右半部分 ，縮小范圍到 右半部分 繼續查找，重復步驟2；

• 如果范圍縮小到只有一個元素，但該元素不等于目標值，則查找失敗，目標值不存在。

• 二分算法的時間復雜度為 O(log n) ，其中 n是序列的長度 。``二分算法 通常適用于 已排序的數據序列，能夠 快速查找目標值 的位置。

<3>. 編寫代碼

class Solution {public int search(int[] nums, int target) {int numslen = nums.length;int left=0,right=numslen-1;while(left <= right) {int mid= left + ((right - left) >>> 1);if(nums[mid] > target) {right = mid - 1;} else if(nums[mid] < target ) {left = mid + 1;} else {return mid;}}return -1;}
}

魚式瘋言

樸素二分的算法體會就是

小了 整體新的區間移動到 中間值的右邊

大了 整體新的區間移動到 中間值的左邊

并且 樸素二分 必須是保證數據是有序的

 while(left <= right) {};

細節注意

我們需要這里要取等的， 當 left 和 right 相等 的時候， 也有可能是 目標值

二. 二分算法的應用

講解完了 樸素的二分算法， 接下來講解了 左右邊界二分查找 算法

小編在這里說一句哦，這個 左右邊界的 二分算法思想

可以這么說，是 基礎算法 細節最多，最惡心 ，也是 最容易造成死循環 的一種算法

1. 尋找峰值

162.尋找峰值題目鏈接

<1>. 題目描述

峰值元素是指其值嚴格大于左右相鄰值的元素。

給你一個整數數組 nums，找到峰值元素并返回其索引。數組可能包含多個峰值，在這種情況下，返回 任何一個峰值 所在位置即可。

你可以假設 nums[-1] = nums[n] = -∞ 。

你必須實現時間復雜度為 O(log n) 的算法來解決此問題。

示例 1：

輸入：nums = [1,2,3,1]
輸出：2
解釋：3 是峰值元素，你的函數應該返回其索引 2。

示例 2：

輸入：nums = [1,2,1,3,5,6,4]
輸出：1 或 5
解釋：你的函數可以返回索引 1，其峰值元素為 2；
或者返回索引 5， 其峰值元素為 6。

題目含義 :

在一個數組尋找一個既 小于左邊 又 小于右邊 的 一個數字的 下標值

<2>. 講解算法思想

其實本質上我們可以認為是尋找一個 極大值(也可以是最大值)

解法一 :

暴力遍歷 :

我們只需要遍歷數組即可查找到我們 極大值

解法二 :

二分算法

當我們需要尋找一個 最大值 的 時候， 我們可以通過 單調性 來尋找 二段性

什么是 二段性 ， 就是在數組中可以區分為 兩個區域 ，我們可以把這個區域劃分為 兩段 ，而這個 兩端 我們可以進行分為

第一個區域的 右邊界 ，以及相鄰的第二個區域的 左邊界

1. 首先我們定義 left 為 第一個元素 下標 ， right 為 最后 一個元素下標

2. 如果 mid 在 遞增 區間， 就讓 left = mid

3. 如果 mid 在 遞減 區間， 就讓 right = mid - 1 ；

4. 最后就是我們需要注意的就是 終止條件 怎么設置

5. 當 遞減區間 邊界的 right 剛好跳到 左邊 ，而 left 也剛剛好處于 遞增區間 的時我們就可以確定右邊界了

所以我們 只需要讓 left 等于 right

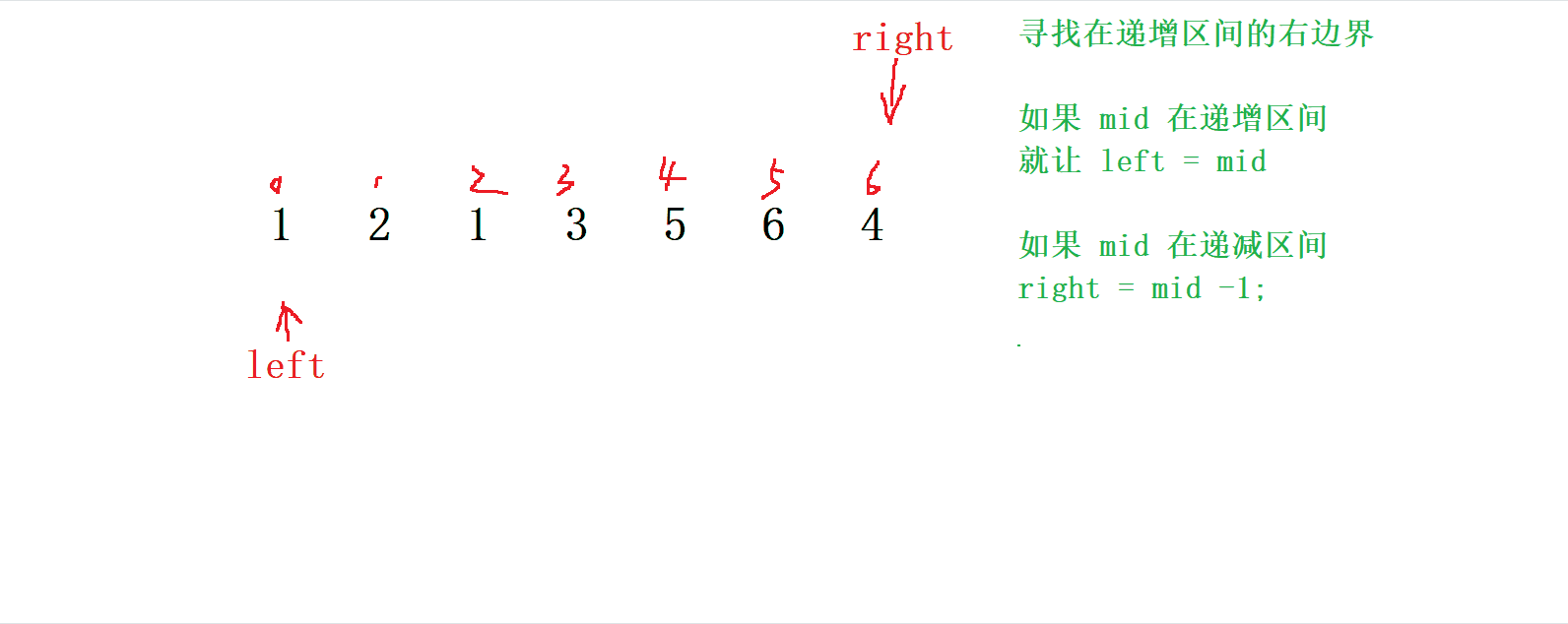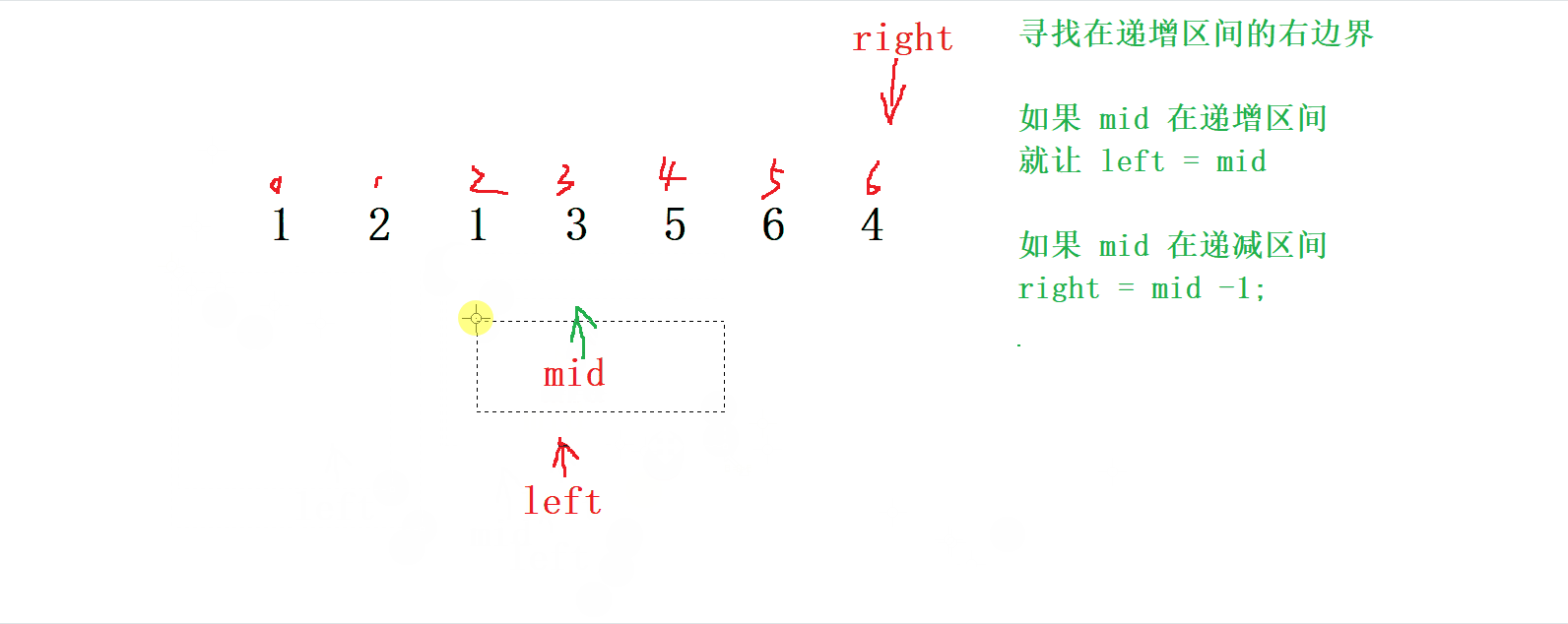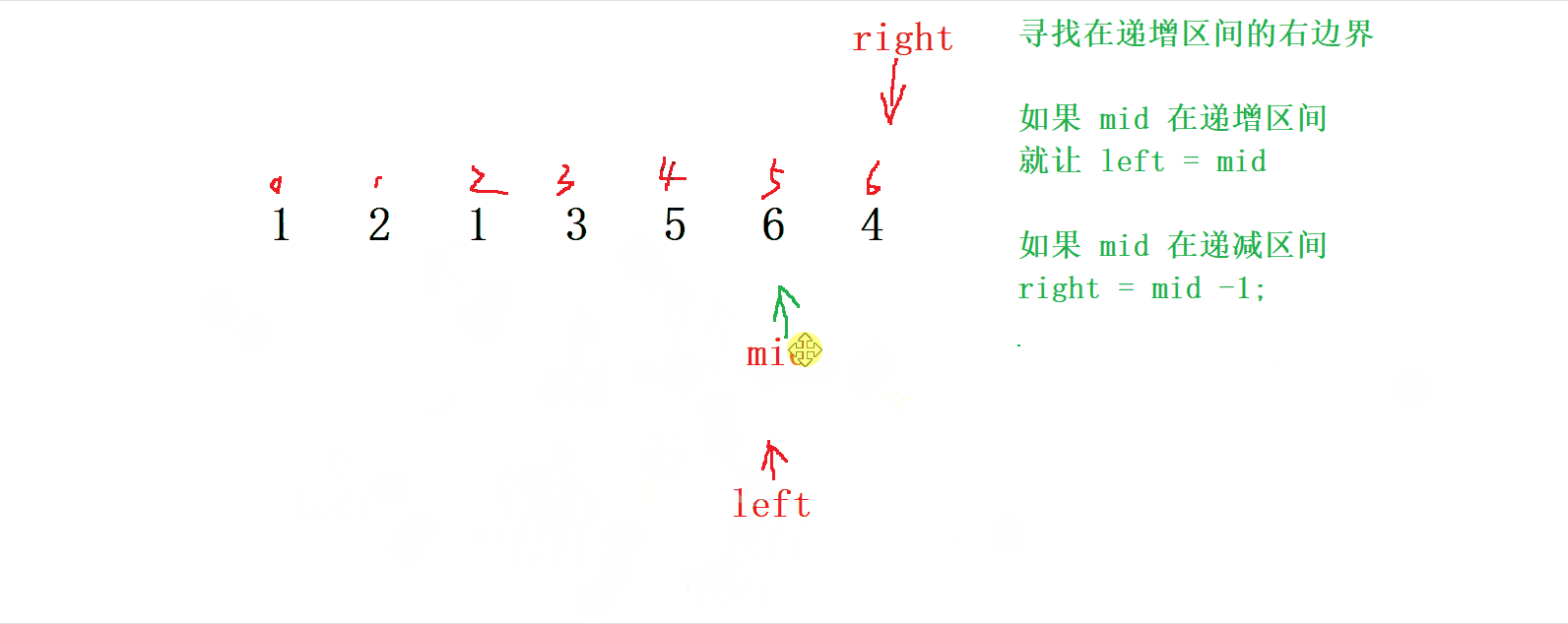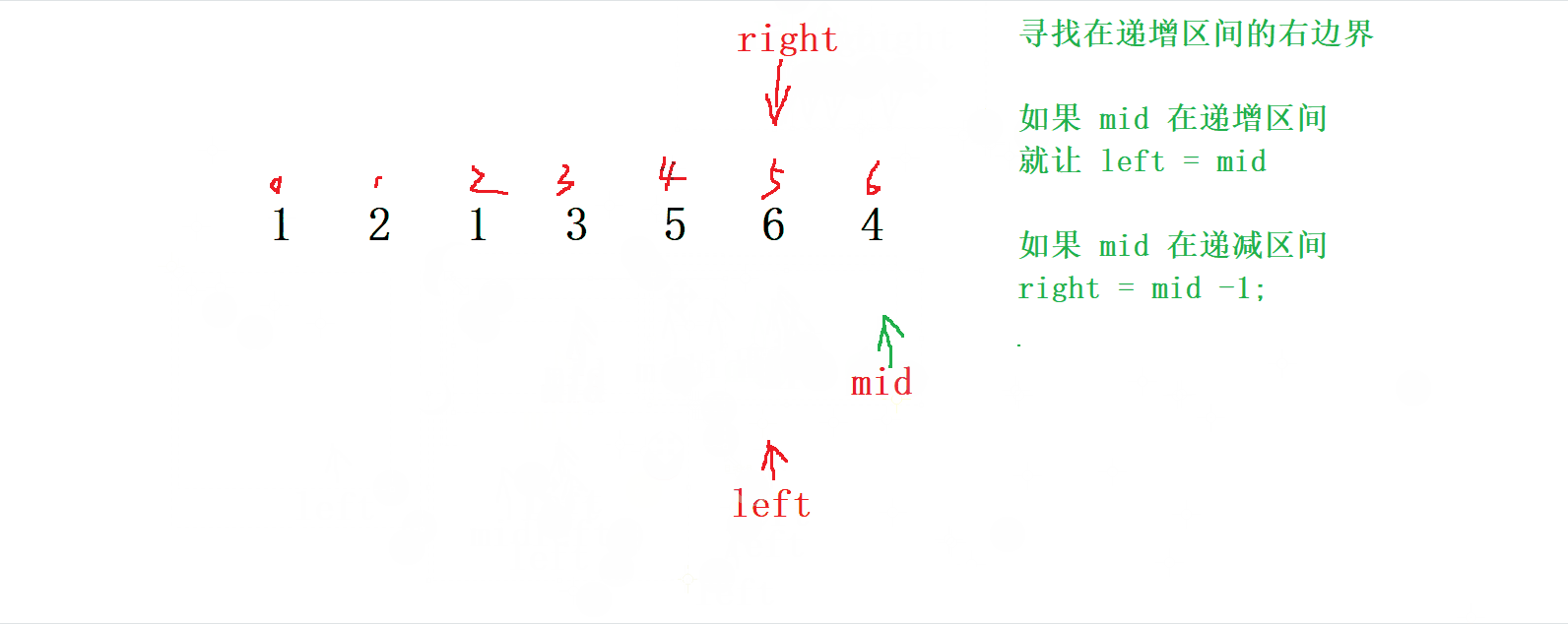
<3>. 編寫代碼

class Solution {public int findPeakElement(int[] nums) {// 進行 左二分查找算法int left=0,right=nums.length-1;while(left < right) {int mid= left +  ( (right - left + 1) >>> 1 );if(nums[mid] > nums[mid-1]) {left = mid;} else {right = mid -1;}}return right;        }
}

魚式瘋言

小編的體會

1. 對于二分算法來說，二段性 才是 核心 , 如何尋找到在 一個區間 中劃分為 兩個 不同含義 的區間，

從而利用二分法尋找左右邊界來得到目標值

本題尋找二段性 常見的方式: 遞增性…

細節處理:

 int mid= left +  ( (right - left + 1) >>> 1 );

這里我們需要用到 當我們用到 right = mid - 1 ;

自然我們就需要 在這里進行 +1 操作

2. 在排序數組中查找元素中 第一個位置和最后一個位置

在排序數組中查找元素中 第一個位置和最后一個位置題目鏈接

<1>. 題目描述

給你一個按照非遞減順序排列的整數數組 nums，和一個目標值 target。請你找出給定目標值在數組中的開始位置和結束位置。

如果數組中不存在目標值 target，返回 [-1, -1]。

你必須設計并實現時間復雜度為 O(log n) 的算法解決此問題。

示例 1：

輸入：nums = [5,7,7,8,8,10], target = 8
輸出：[3,4]
示例 2：

輸入：nums = [5,7,7,8,8,10], target = 6
輸出：[-1,-1]
示例 3：

輸入：nums = [], target = 0
輸出：[-1,-1]

題目含義 :

尋找一段相同目標值的 第一個位置 和 最后一個位置 的 下標

<2>. 講解算法思想

題目分析:

用的還是二分思想，就是根據數據的性質，在某種判斷條件下將區間 一分為二 ，然后舍去其中一個
區間，然后再另一個區間內查找；方便敘述，用 target 表示該元素， left 表示 左邊界， right 表示右邊界。

當我們求左邊界時， 就可以按照

尋找左邊界：

• 我們注意到以左邊界劃分的兩個區間的特點：

• 左邊區間 [left, left - 1] 都是小于 target 的；

• 右邊區間（包括左邊界） =[left, right] 都是 大于等于 x 的；

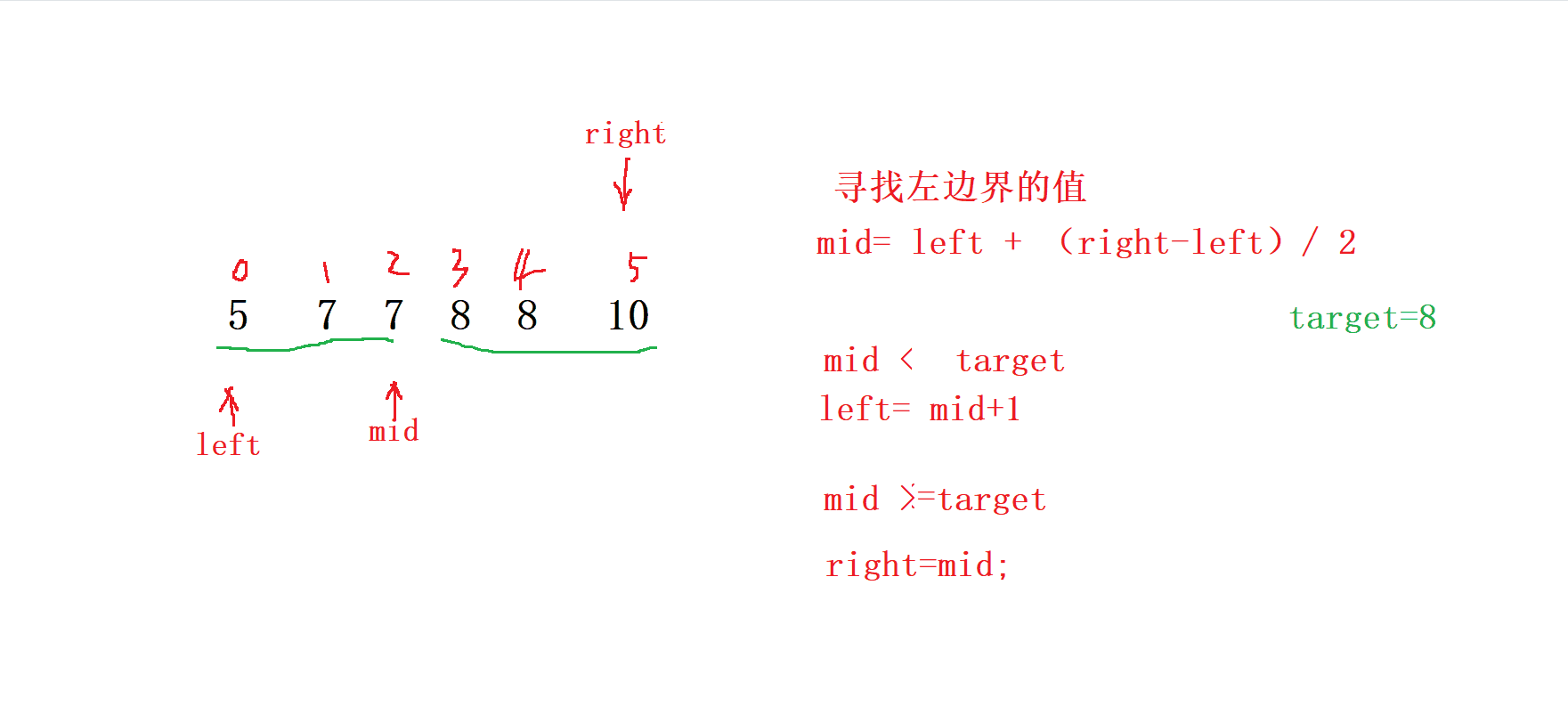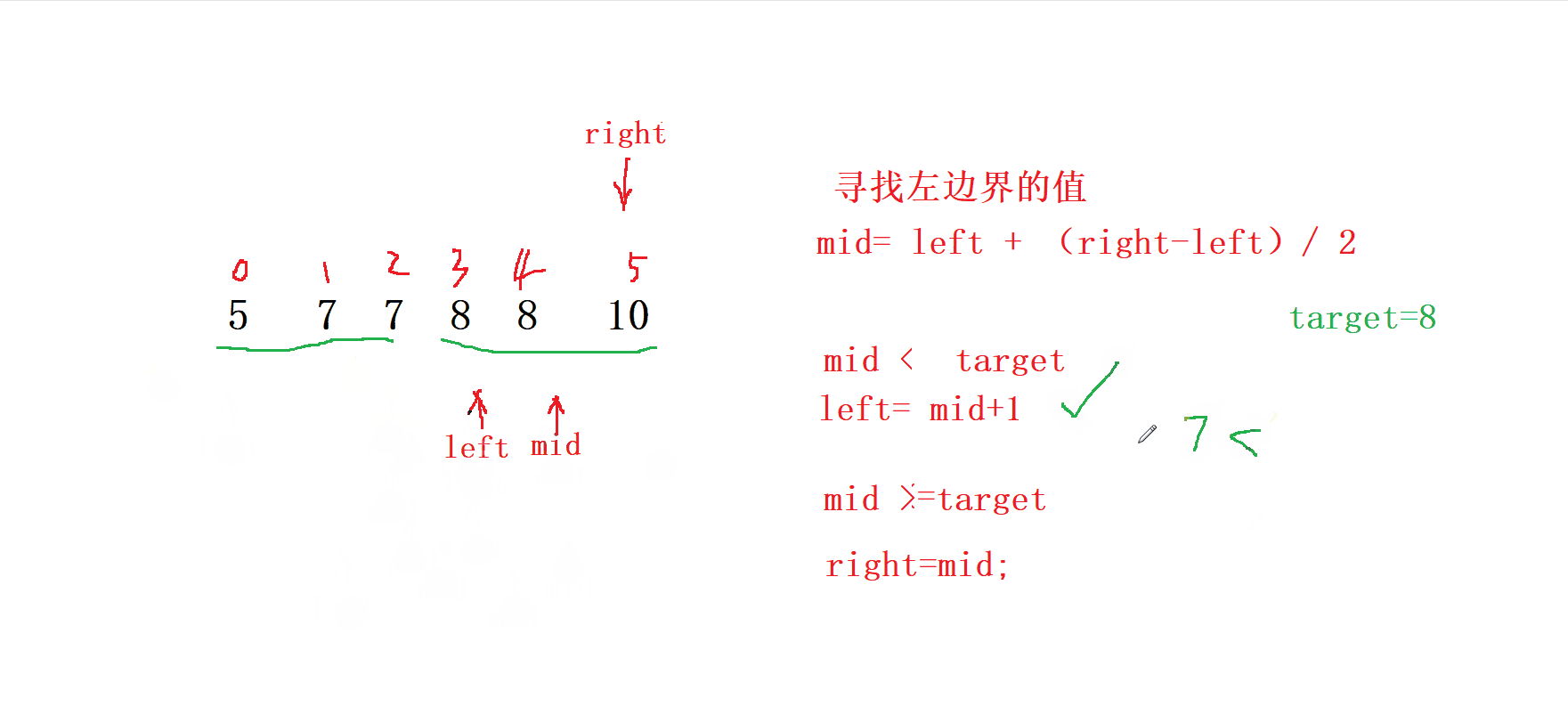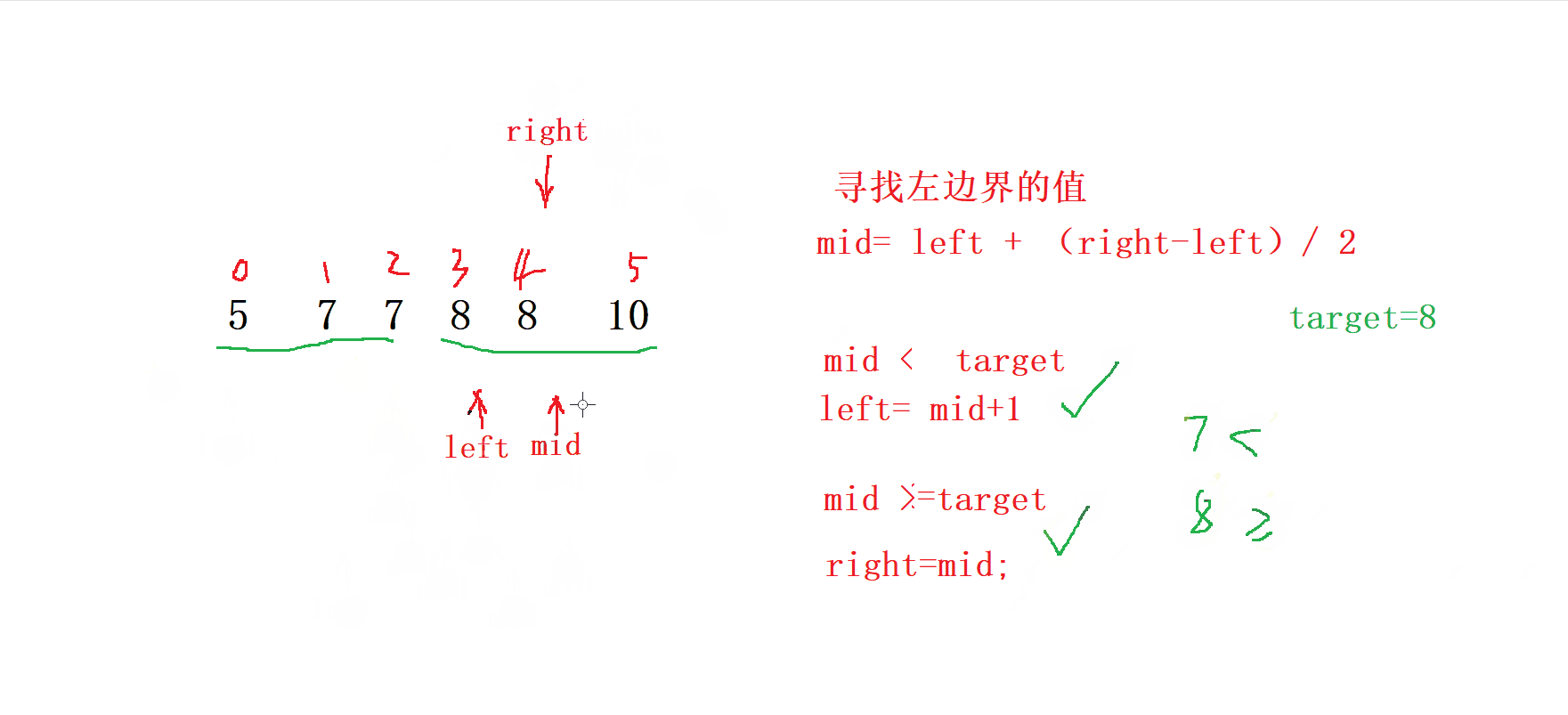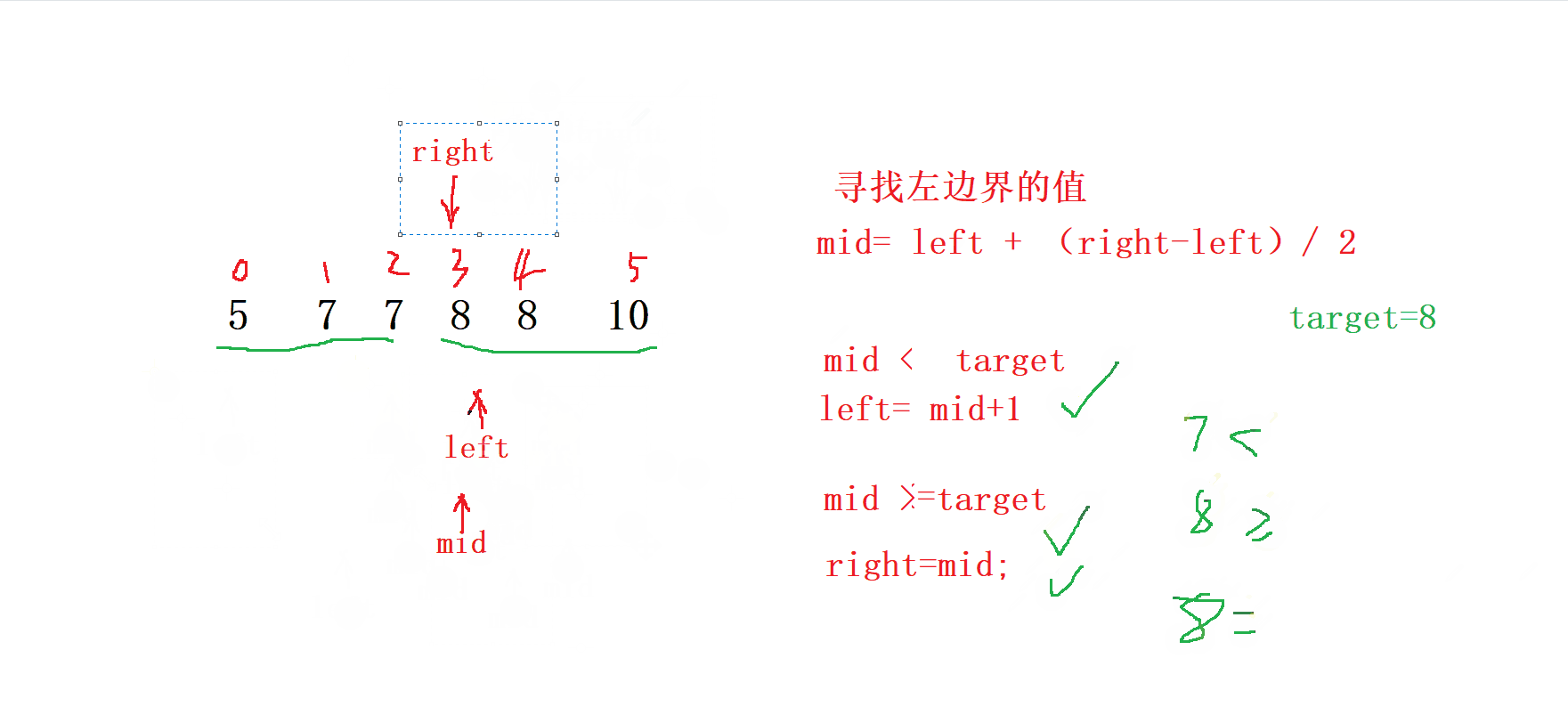
• 因此，關于 mid 的落點，我們可以分為下面兩種情況：

• 當我們的 mid 落在 [left, left - 1] 區間的時候，也就是 arr[mid] <
  target 。

• 說明 [left, mid] 都是可以舍去的，此時更新 left 到 mid + 1 的位置，
  繼續在 [mid + 1, right] 上尋找左邊界；

• 當 mid 落在 [left， right] 的區間的時候，也就是 arr[mid] >= target 。
  說明 [mid + 1, right] （因為 mid 可能是最終結果，不能舍去）是可以舍去的，此時
  更新 right 到 mid 的位置，繼續在 [left, mid] 上尋找 左邊界；

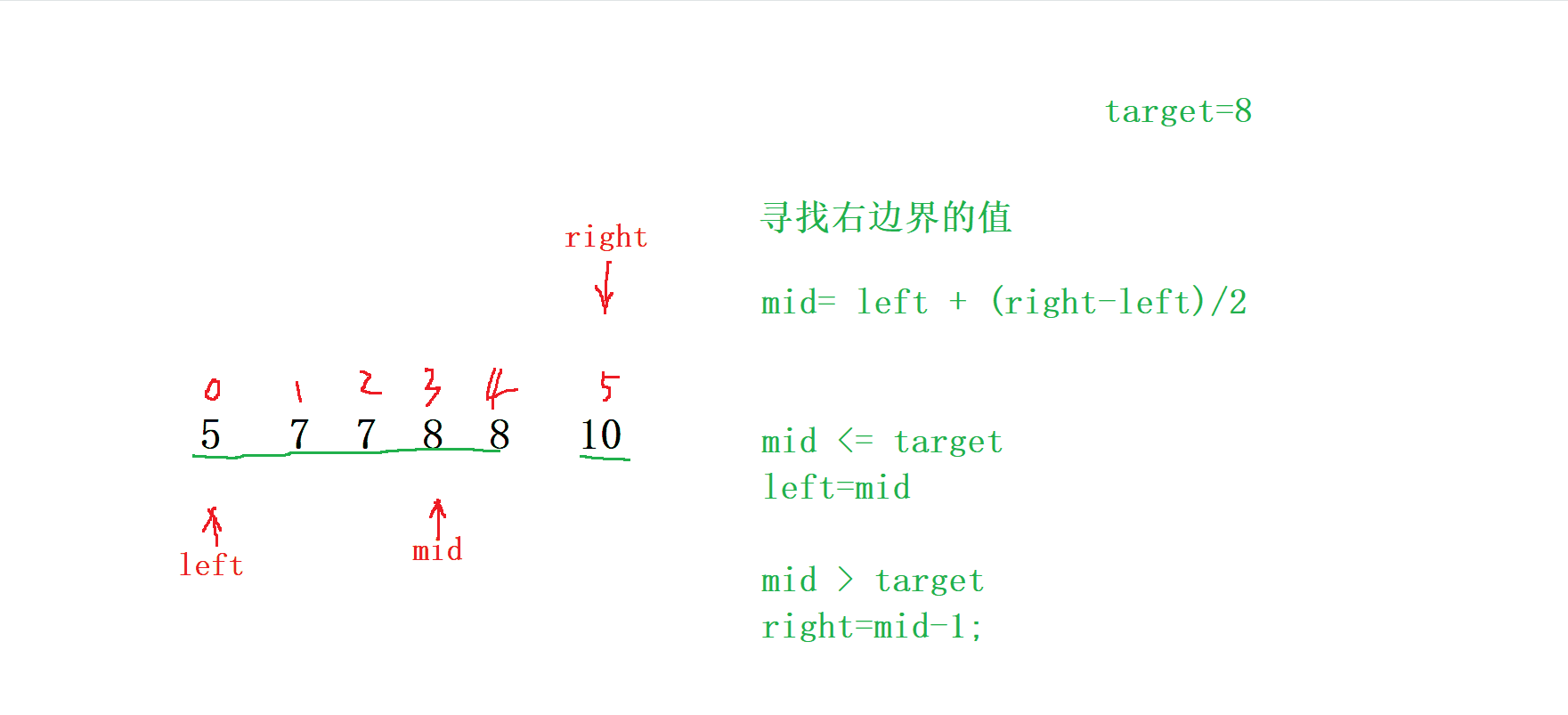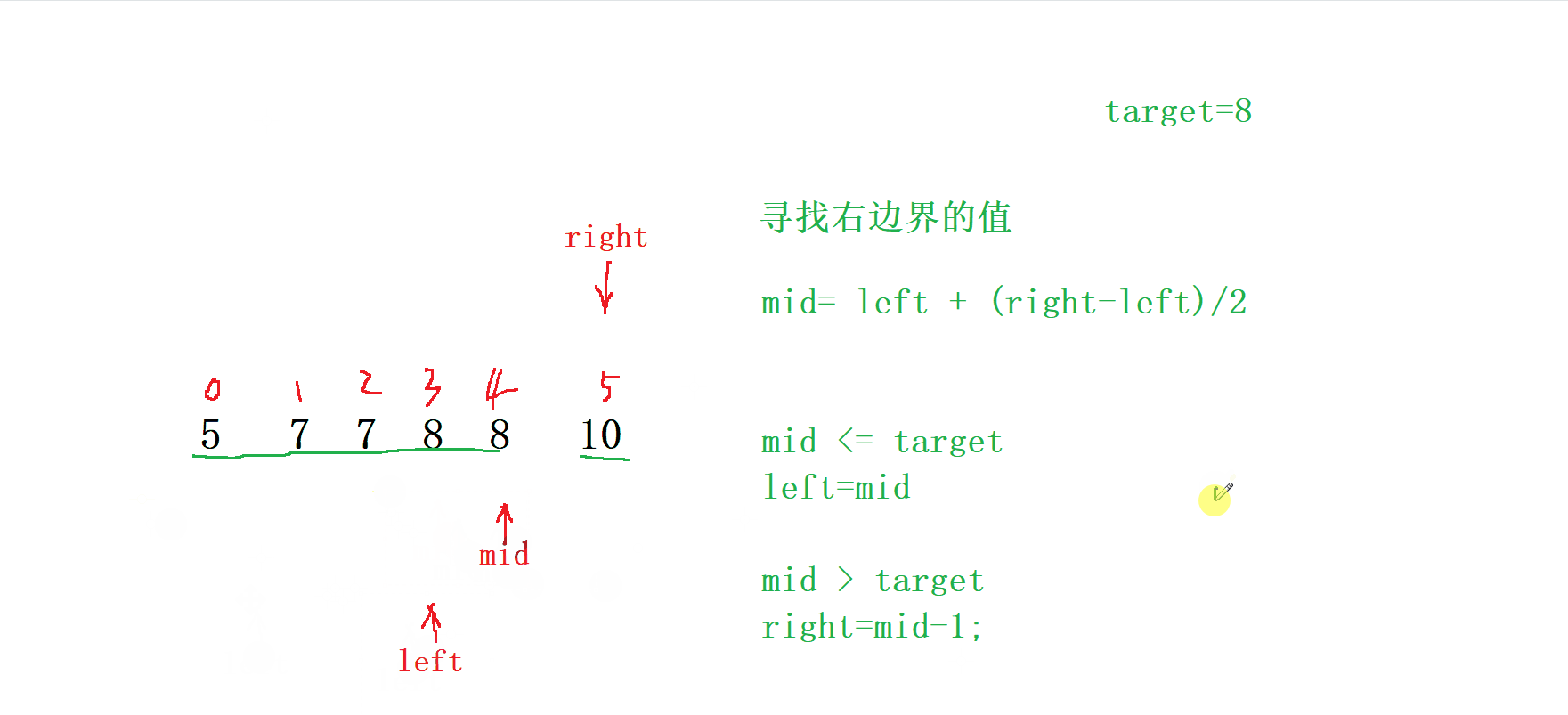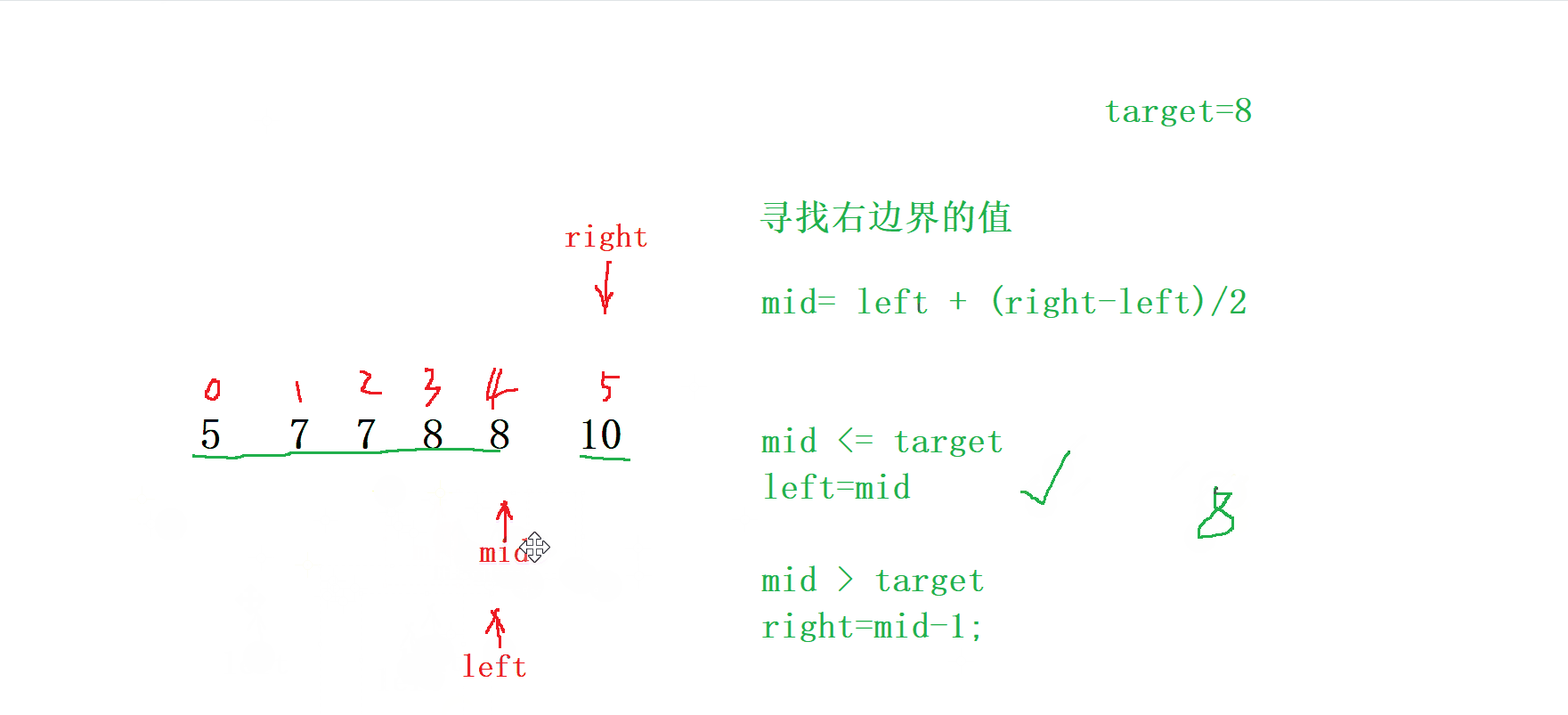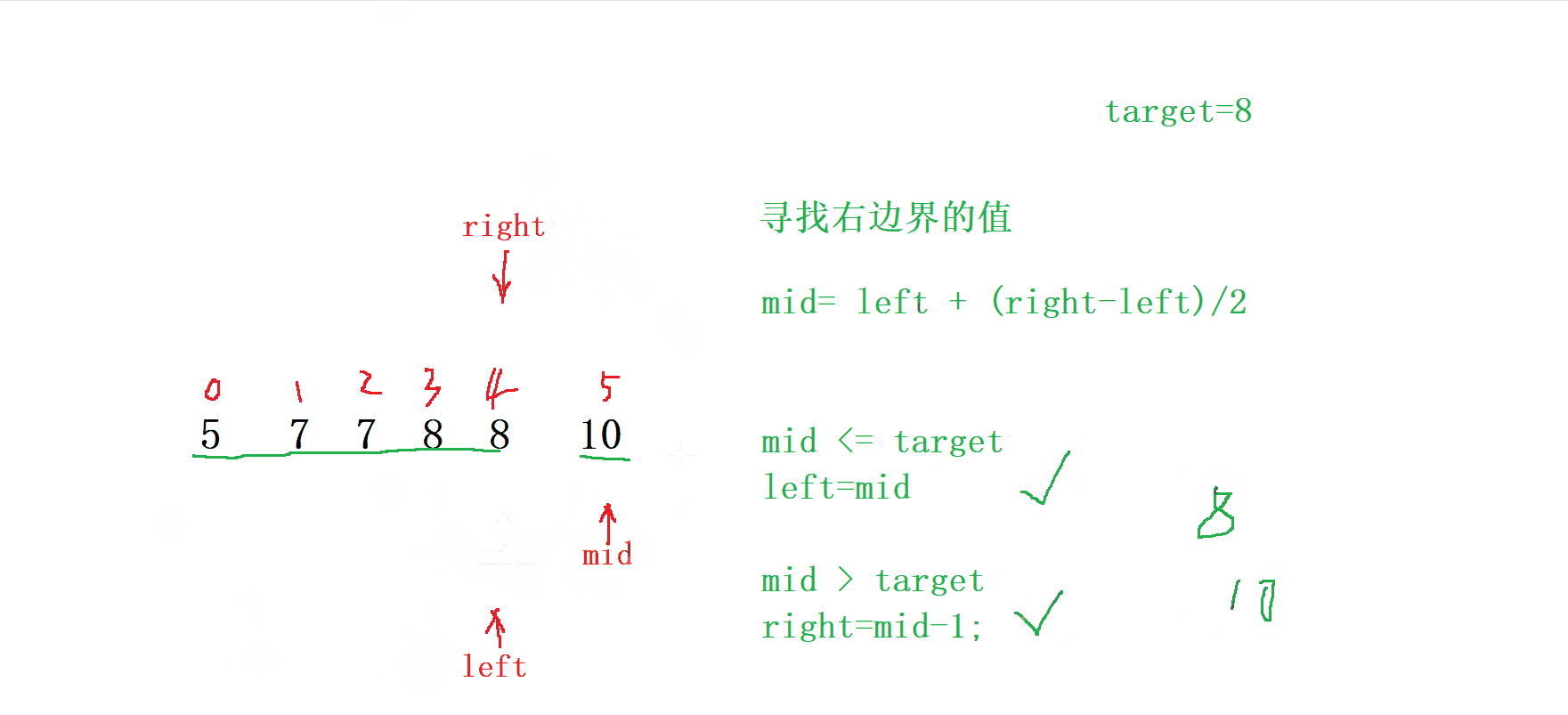
當我們需要右邊界時

按照上面我們尋找 左邊界 的思維來尋找 右邊界

我們就以 右邊界 的來劃分區域

當 mid 處于 <= target 時 ，right = mid；

當 mid 處于 > target 時 ， left = mid -1；

<3>. 編寫代碼

class Solution {public  int[] searchRange(int[] nums, int target) {// 定義一個存放起始和終止位置的數組int[] ret=new int[]{-1,-1};// 得到長度int len=nums.length;// 數組為 空 時 就直接返回if(len == 0) return ret;// 進行二分操作// 定義左右指針int left=0,right= len-1;/*** 尋找左邊界* 當 right = mid = left 就會陷入死循環* 細節一 : 終止條件 不能寫等號** 當 中點值  <= target 時* 細節二 ： 我們更新 left = mid** 當 left  mid  right  相鄰 時*  細節三 ： 更新 mid = left + ( (right - left + 1) >>> 1 )**///while(left < right) {int mid=left + ( (right-left) >>> 1);if(nums[mid] < target) {left = mid+1;}  else if(nums[mid] >= target) {right = mid ;}}if(nums[right] == target) ret[0] = right;left=0;right=len-1;/*** 尋找右邊界**  當 right = mid = left 就會陷入死循環*  細節一 : 循環終止條件 ： 這里不可以進行 取等**  當 中點值 >= target  時 進行 right 移動*  細節二 : 右指針 right 移動的位置 是 到達  中點下標 mid***  left  mid  right*  當 中點 和 left  right 相鄰 時就需要*  細節三 : 確立 mid = left +(  (right - left ) >>> 1 )*/while(left < right) {int flg=left + ( (right - left + 1) >>> 1);if(nums[flg] <= target) {left = flg;}  else if(nums[flg] > target) {right = flg -1;}}if (nums[left]== target) ret[1]= left;return ret;}
}

魚式瘋言

說下對于本題小編個人的體會吧

二段性 我們是找到了，但這里的是如何去 劃分我們的區域

所以然后選擇 等號 也是很關鍵的一條

當我們尋找 左邊界 時，我們就需要 讓 mid >= target 的情況進行劃分

當我們尋找 右邊界 時， 我們就需要 讓 mid < target 的情況進行劃分\

細節處理

處理 右邊界 的時

 while(left < right) {}

當 right = mid = left 就會陷入 死循環

細節一 :

終止條件 不能寫等號

   if(nums[flg] <= target) {left = flg; }

當 中點值 <= target 時

細節二 ：

我們更新 left = mid

當 left mid right 相鄰 時

細節三 ：

更新 mid = left + ( (right - left + 1) >>> 1 )

處理 左邊界 時

 while(left < right) {}

當 right = mid = left 就會陷入 死循環

細節一 :

終止條件 不能寫等號

   if(nums[flg] >= target) {right = flg; }

當 中點值 <= target 時

細節二 ：

我們更新 right = mid

當 left mid right 相鄰 時

細節三 ：

更新 mid = left + ( (right - left ) >>> 1 )

3. 尋找排序數組中的最小值

尋找排序數組中的最小值題目鏈接

<1>. 題目描述

已知一個長度為 n 的數組，預先按照升序排列，經由 1 到 n 次 旋轉 后，得到輸入數組。例如，原數組 nums = [0,1,2,4,5,6,7] 在變化后可能得到：

若旋轉 4 次，則可以得到 [4,5,6,7,0,1,2]

若旋轉 7 次，則可以得到 [0,1,2,4,5,6,7]

注意，數組 [a[0], a[1], a[2], …, a[n-1]] 旋轉一次 的結果為數組 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

給你一個元素值 互不相同 的數組 nums ，它原來是一個升序排列的數組，并按上述情形進行了多次旋轉。請你找出并返回數組中的 最小元素 。

你必須設計一個時間復雜度為 O(log n) 的算法解決此問題。

示例 1：

輸入：nums = [3,4,5,1,2]
輸出：1
解釋：原數組為 [1,2,3,4,5] ，旋轉 3 次得到輸入數組。

示例 2：

輸入：nums = [4,5,6,7,0,1,2]
輸出：0
解釋：原數組為 [0,1,2,4,5,6,7] ，旋轉 3 次得到輸入數組。

示例 3：

輸入：nums = [11,13,15,17]
輸出：11
解釋：原數組為 [11,13,15,17] ，旋轉 4 次得到輸入數組。

** 題目含義** ：

在一個由原先 有序 進行 旋轉 后的數組中，尋找 最小值

<2>. 講解算法思想

題目分析

因為題目要求時間 復雜度只能是 O(log n)

所以這樣我們就需要用到 二分算法

那我們就必須尋找到 二段性

首先還是利用的大小關系來尋找我們的 基準值

因為是 反轉后的數據，所以從最小值到最后一個元素必然是 遞增 的，

那么這段區間肯定都是 小于等于 最后一個元素的

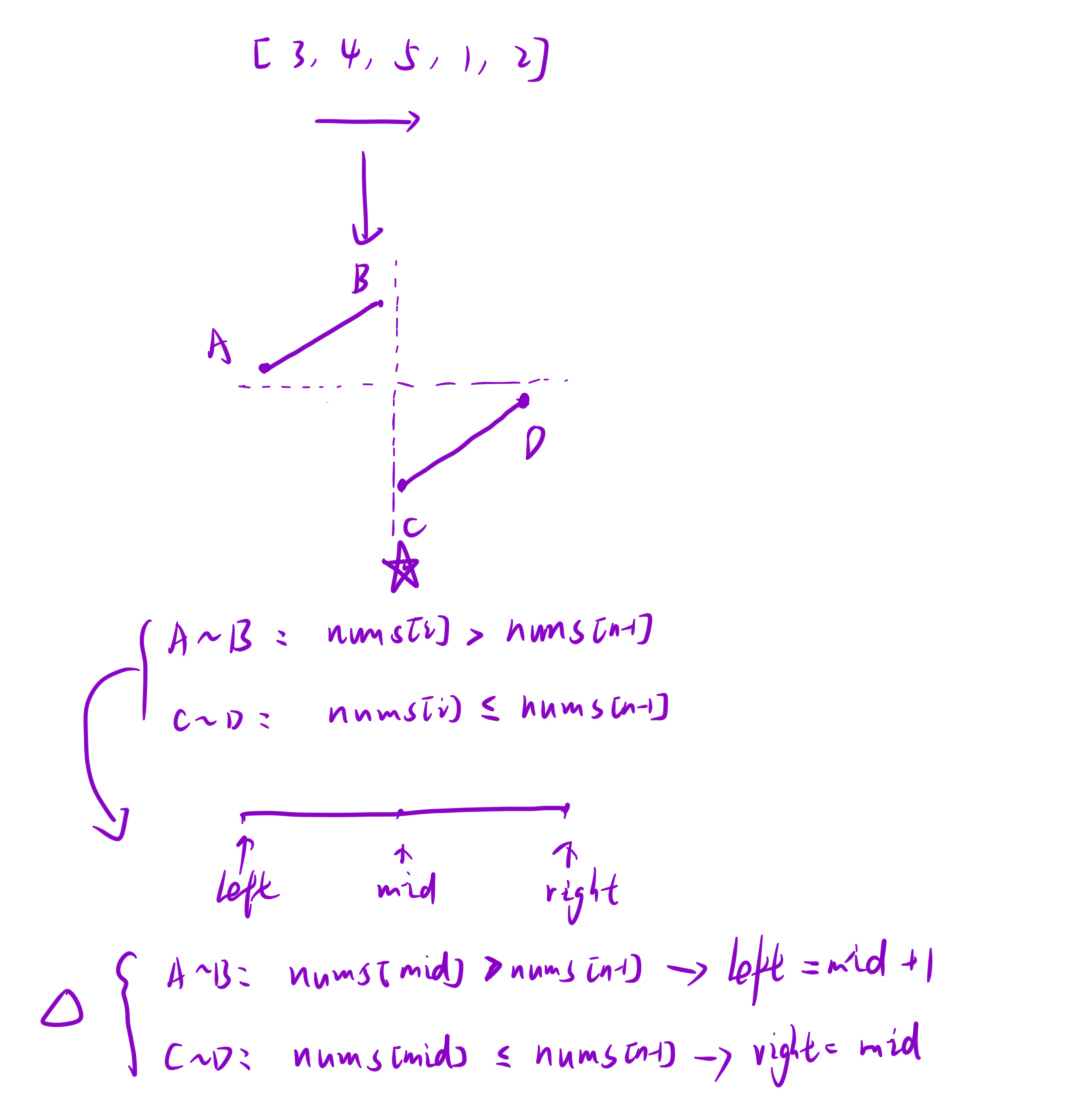
而 翻轉過去的元素 必然是 大于 我們最后一個元素的，我們又劃分出了 這段區間

** 二分算法**

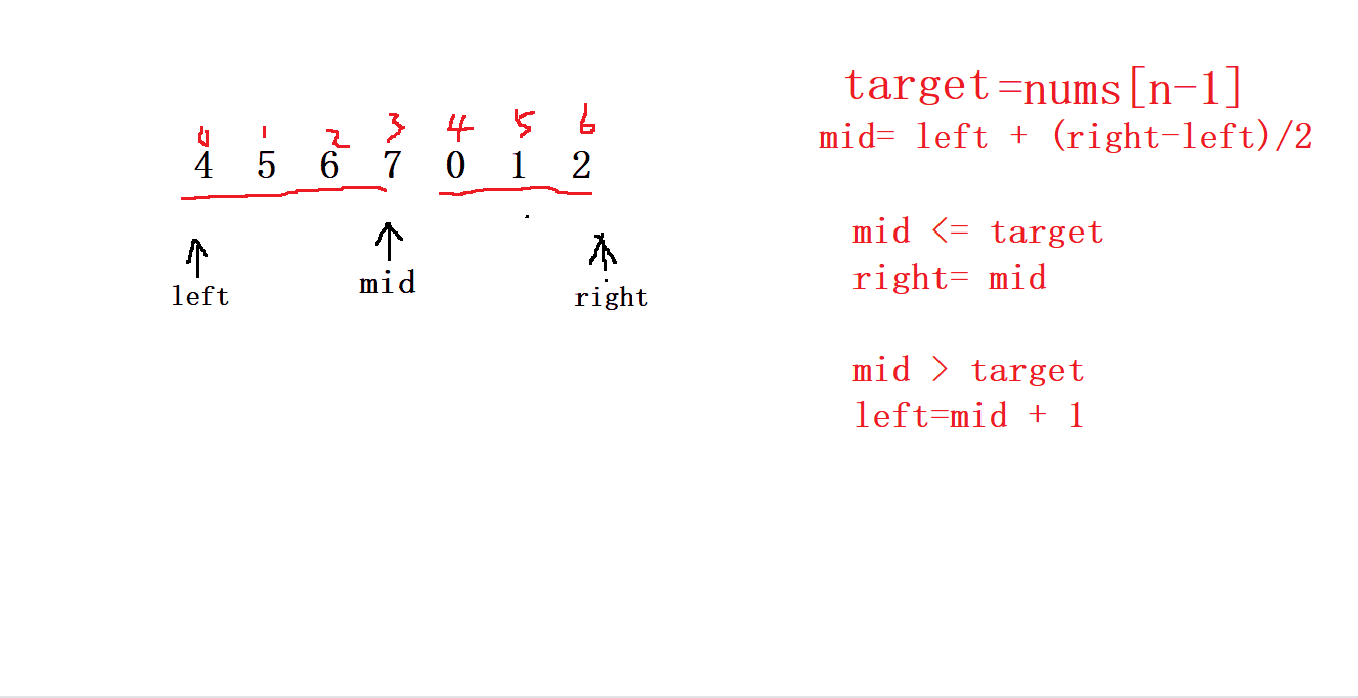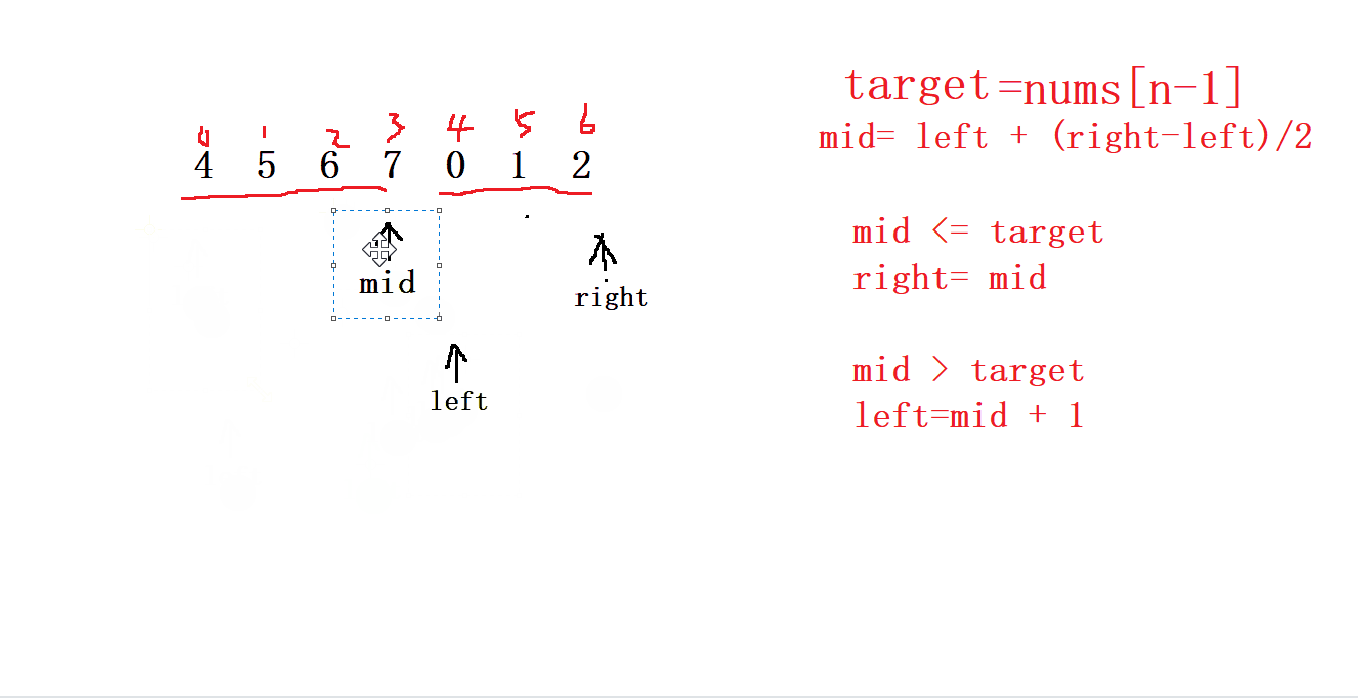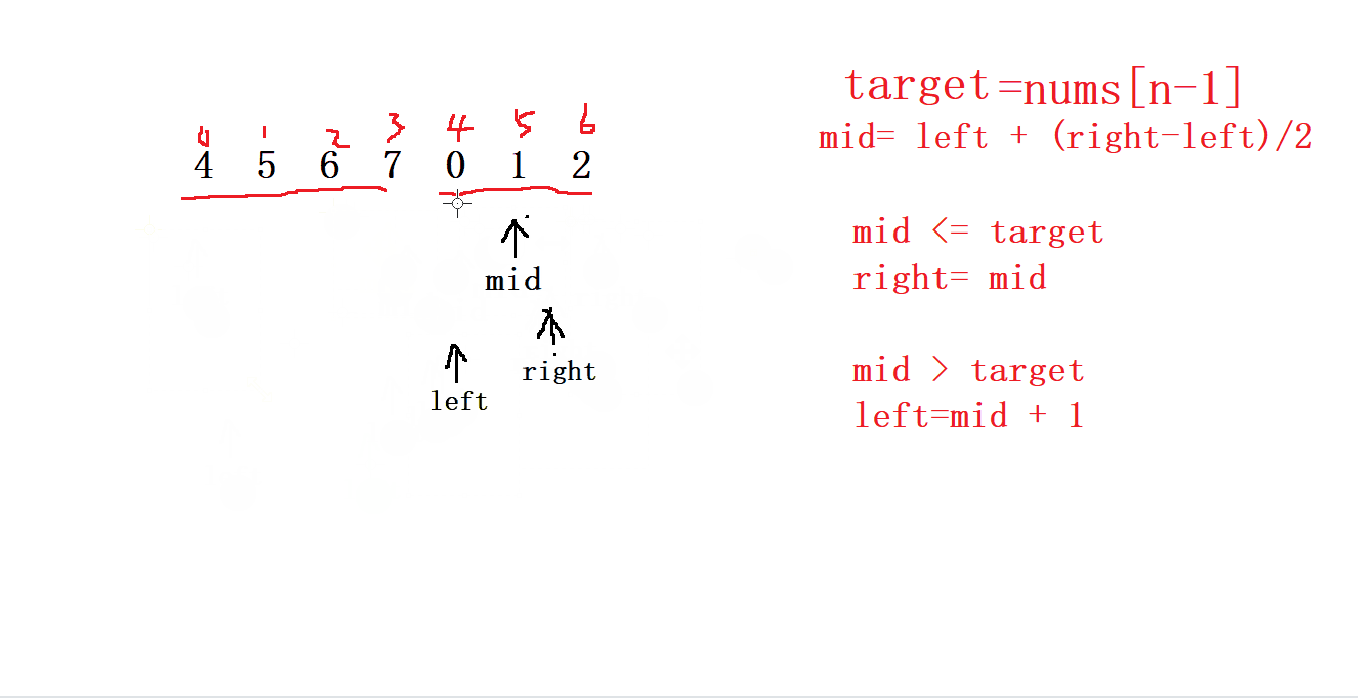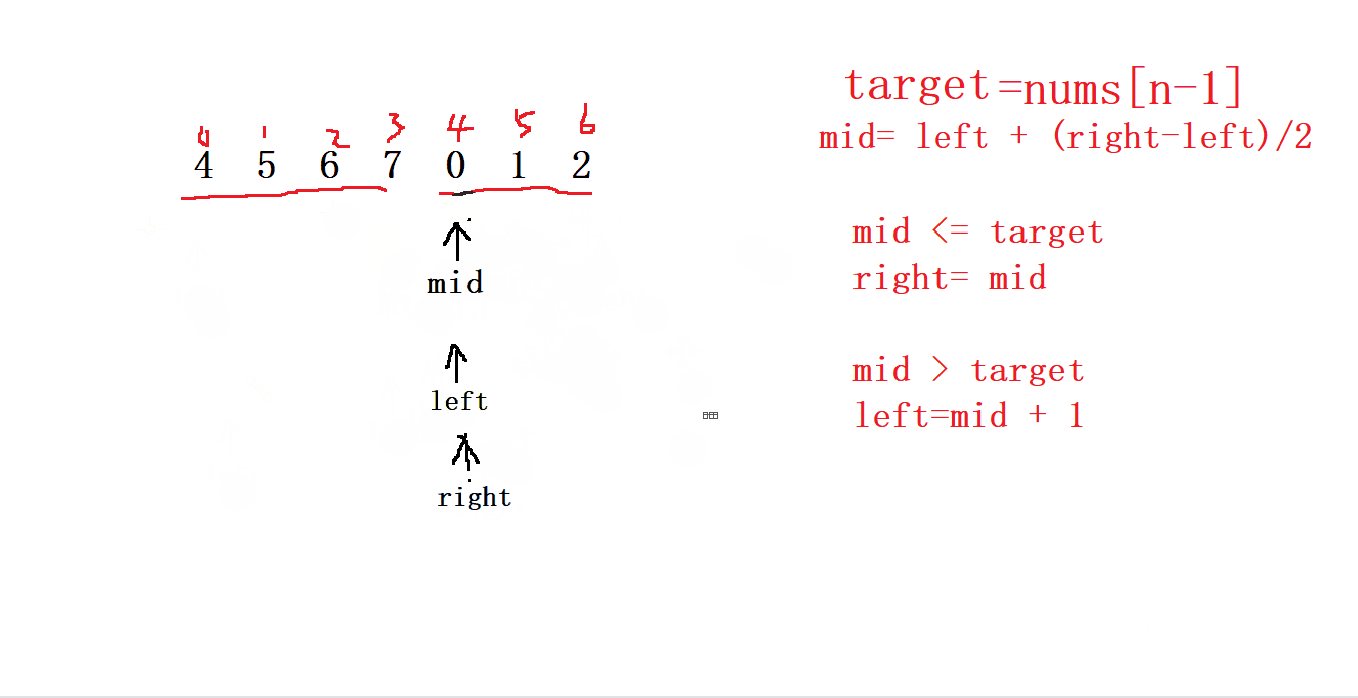
所以我們操作數字定義 left= 0 ，right 指向最后一個元素 ， 并且取一個 基準值 target 也為最后一個元素

然后進行 mid 的判斷，以及 right 和 left 的移動,

最終 left 和 right 相遇的位置就是我們要找的 最小值

<2>.編寫代碼

class Solution {public int findMin(int[] nums) {// 進行二分左查找 int left= 0, right=nums.length-1;// 以 最右邊為基準值 進行 原數組的劃分int flg=nums[right];while(left < right) {// 得到中間 下標int mid= left + (  (right - left ) >>> 1 );// 如果 小于 基準   說明 是 左邊的數 ， 不存在最小值if( nums[mid]  >  flg) {left = mid +1;} else {// 存在 右邊 小于或等于 基準值    right =mid;}}  return nums[left];}}

三. 二分算法的總結

我們先初步認識了什么是 二分算法以及并明白了 樸素二分查找算法 的使用，

并且 樸素 是在 有序 的條件下進行

之后我們又通過 “尋找峰值”，“在排序數組中查找元素中 第一個位置和最后一個位置”，"尋找排序數組中的最小值" , 我們更明白 尋找 二段性 比如通過 比大小, 單調性， 端點值, 不等性

下面有 小彩蛋哦

總結樸素二分算法模板

總結左右邊界二分算法模板

記住一點：

求左邊界時： right = mid

求右邊界時： left = mid

如果覺得小編寫的還不錯的咱可支持 三連 下 (定有回訪哦) , 不妥當的咱請評論區 指正

希望我的文章能給各位寶子們帶來哪怕一點點的收獲就是 小編創作 的最大 動力 💖 💖 💖