通過一個例子來引出卡爾曼濾波的狀態更新方程；

這里系統狀態是金條的重量；

為了估計系統的狀態，我們可以多次測量金條的重量，然后求平均值；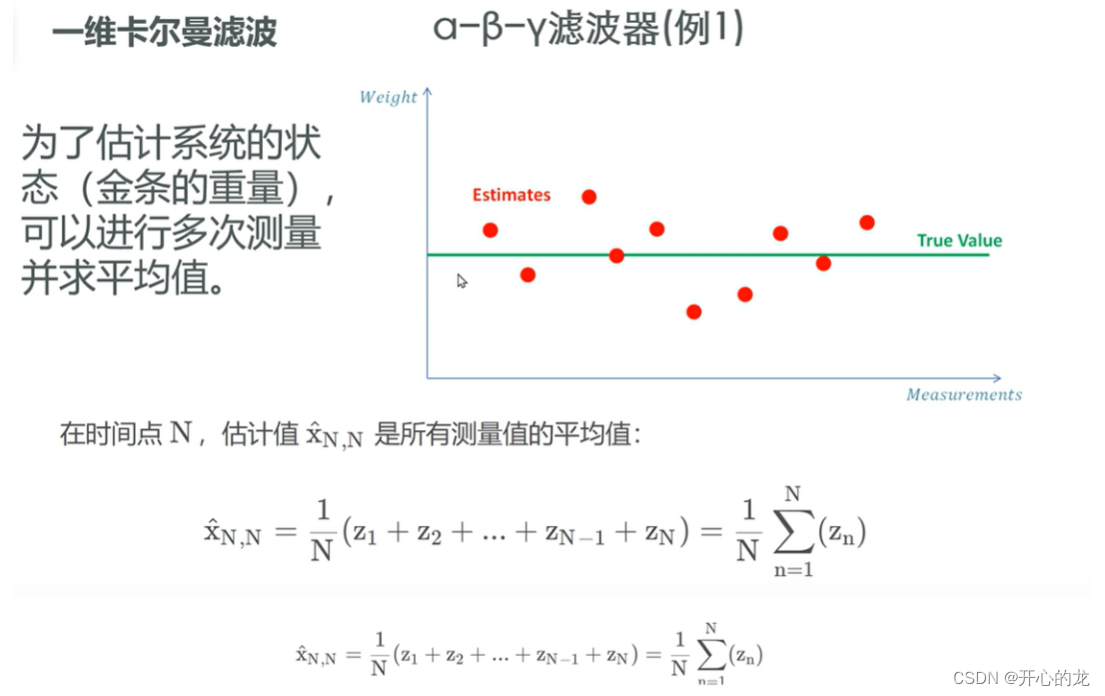

?其中估計值是所有測量值的平均值；

?

由于我們使用的是靜態模型（金條的重量是不會在短時間內發生改變的），所以第N次的估計值和N+1次的估計值相等，即

?

?

具體的物理意義：

1.預測重量的調整：表示測量值Zn和先驗估計值（測出第N-1次后，對第N次的估計）之間的差異，稱為殘差或者創新，這個差異代表了當前的測量值和先前預測的偏差；

加權平均:通過乘以權重因子，濾波器調整對這個差異的響應，較大的權重因子，表示更信任當前測量值，較小的權重因子表示更信任先前的預測；

更新后的估計位置：通過將加權的殘值添加到預測重量，得到更新的后的估計重量，這意味著新的估計重量是預測重量和測量重量之間的加權平均，更加接近實際重量；

其中1/N隨著測量次數越來越小，意味著開始時沒有足夠的重量信息，估算值主要依靠測量值，但是隨著次數越來越多，每次測量的值在估計過程中占比也越來越少，隨著迭代次數足夠多，新的測量值對估計值的影響可以忽略不記；??

在做第一次測量之前，可以通過看金條上刻的數字(或粗略估計)得到金條的重量，著稱為初始猜測(Initial Guess)，它將是我們的第一個估計；

這個估計并不會影響我們后面的結果，隨著測量次數逐漸增大，最后估計的結果都會趨于真實值，這就是濾波器的厲害之處；

在卡爾曼濾波器中1/N這個權重因子就是卡爾曼增益 ；

這個方程的形式就是狀態更新方程，如下：

?

狀態更新方程只是卡爾曼濾波的一個方程，卡爾曼濾波是一個有機整體，具體流程如下：

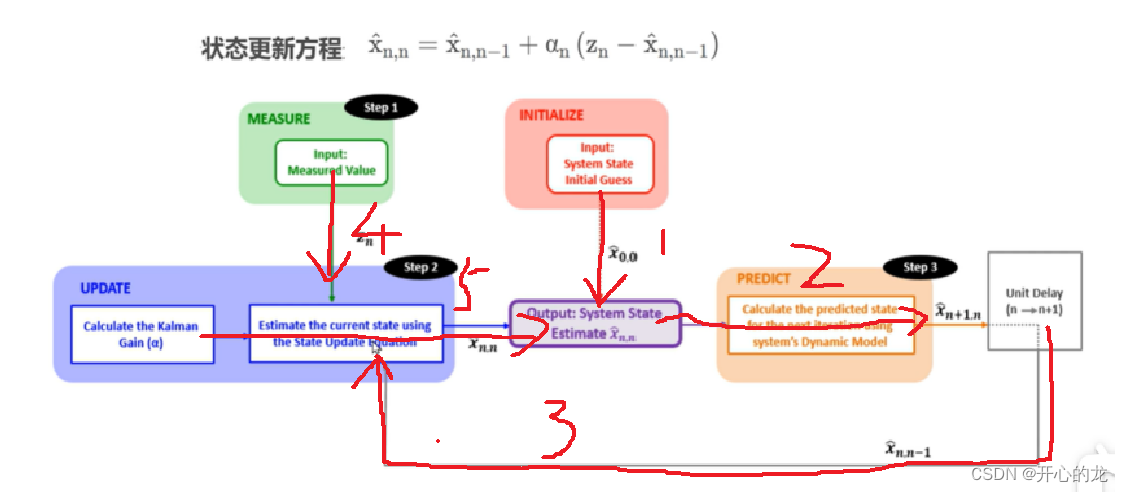
流程并不是按照Step1.2.3進行的，具體如圖所示：

?

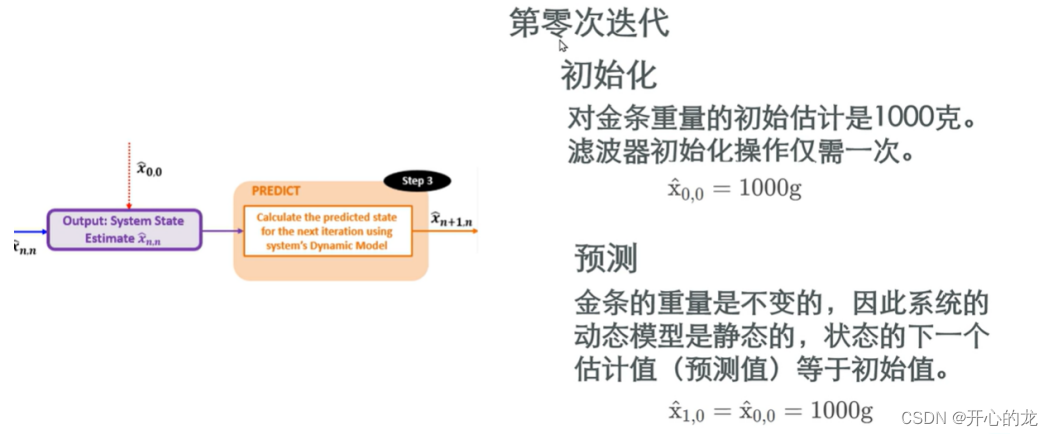
首先第一步1：進行初始化，我們根據各方面因素，輸入一個估計值X（0，0）（主觀定義）；

第二步2：進行預測（狀態外推方程），但是由于我們目前使用的是靜態模型，所以預測前后結果保持不變，得到輸出估計值為X(1,0)（表示先驗估計值，第0次對第一次的估計，其值仍然等于X（0，0））；

第三步3：變為下一時刻n->n+1，此時N=1;

第四步4：進行測量，輸入測量值Z1；

第五步5：根據狀態更新方程，更新數據得到下一時刻的估計值，之后（初始化只進行一次）進行預測，由于我們是靜態模型，所以不需要進行任何預測，值保持不變，循環往復；

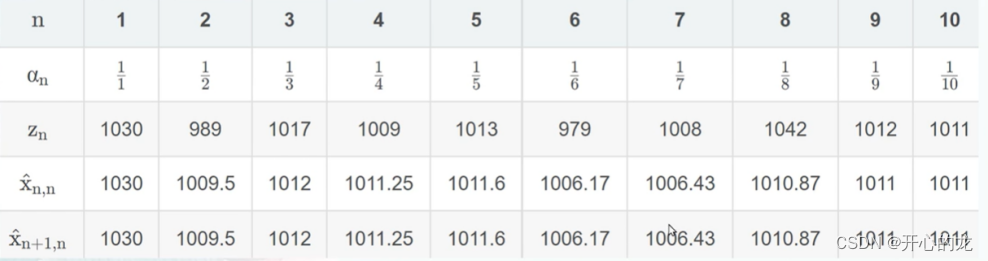
....經過十次后，得到以下結果：

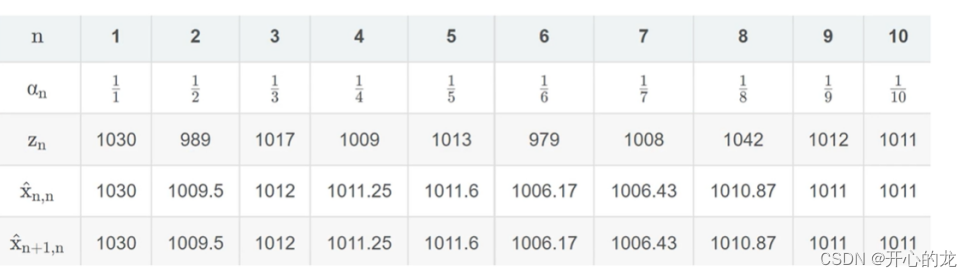?繪制圖像：綠色的線是真實值，藍色的線是測量值，紅色的線是估計值，隨著迭代次數，估計值收斂于真實值；

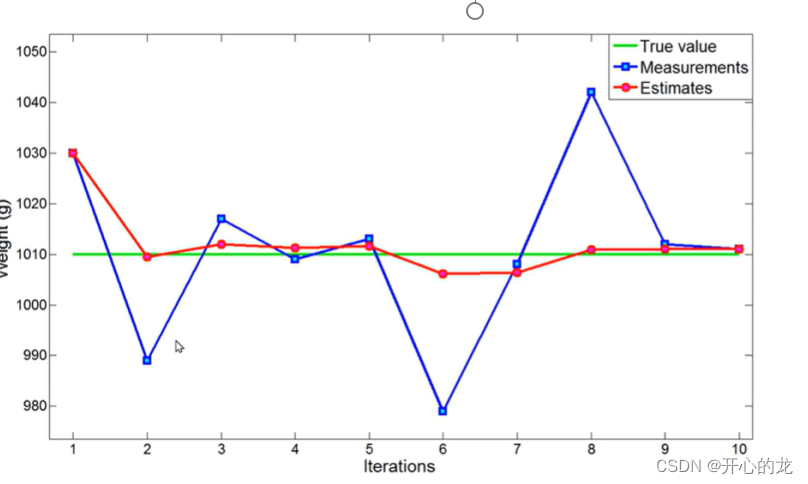
?具體舉例：

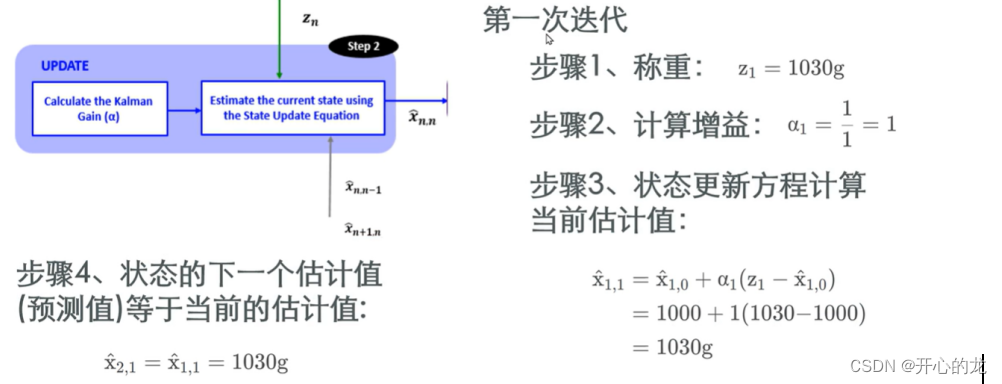?第二次迭代：

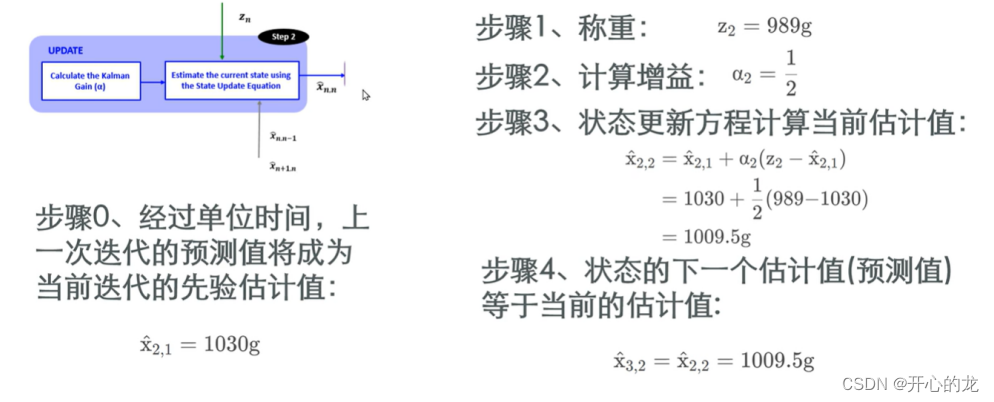
第三次迭代：

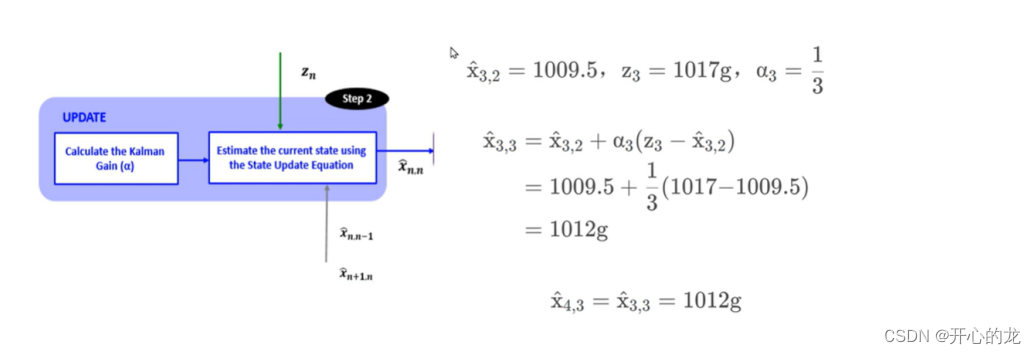?增益隨著測量的次數而減小，每一次測量值的影響都比之前前一個測量值小；

?

在這個例子中，我們為靜態系統設計了一個簡單的估計算法，并且推導出了卡爾曼濾波的五個方程之一的狀態更新方程。

系統的輸入是上一時刻的先驗估計值和權重因子，輸出是當前時刻的估計值；

表示通過預測值加上殘差（測量值減去預測值）*權重因子得到當前時刻的估計值，更加接近實際重量；

?
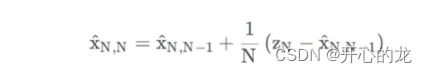