目錄

?編輯

1.前言

2.四道題目

1.小紅叕戰小紫

1.題目描述

2.輸入描述

3.輸出描述

4.示例

5.題解與思路

2.小紅的數組移動

1.題目描述

2.輸入描述

3.輸出描述

4.示例

5.題解與思路

3.小紅的素數合并

1.題目描述

2.輸入描述

3.輸出描述

4.示例

5.題解與思路

4.小紅的子序列求和

1.題目描述

2.輸入描述

3.輸出描述

4.示例

5.題解與思路

3.小結

---

1.前言

哈嘍大家好喔，今天來給大家帶來牛客周賽42部分題目的題解，無論你是小白，還是大牛，你一定都是能看懂的，希望對大家有所幫助，也歡迎大家多多交流，提出不一樣但同樣很有價值的看法。

2.四道題目

1.小紅叕戰小紫

1.題目描述

2.輸入描述

3.輸出描述

4.示例

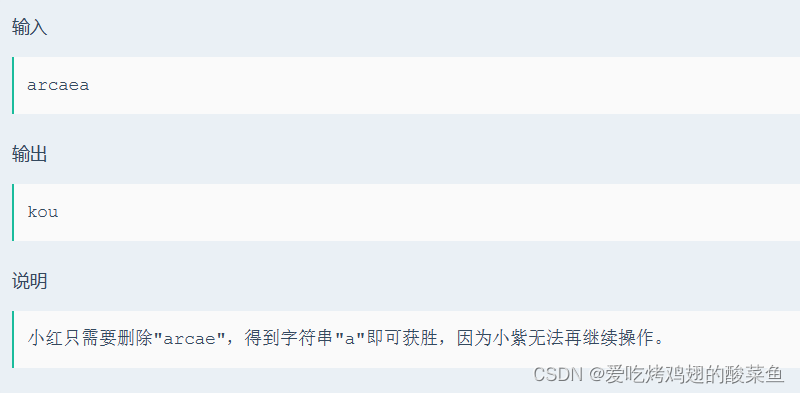
5.題解與思路

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;int main(){char a[15];scanf("%s",a);int i=strlen(a);if(i!=1)printf("kou");else printf("yukari");return 0;
} 

這道題就好像一道腦筋急轉彎一樣，需要簡單思考一下，代碼量不大，作為簽到題也是蠻有趣的。思路：由于每一次小紅都可以刪除多個前綴或后綴字符，所以當字符串大于1時，小紅只需要將字符串刪到1即可，此時小紅就贏。但如果本身字符串長度就為1，則小紫贏。

2.小紅的數組移動

1.題目描述

2.輸入描述

3.輸出描述

4.示例

5.題解與思路

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
long long num[100005];
long long ans = 0, n = 0, locate = 0;
char order[100005];int main() {scanf("%lld",&n);for (int i = 0; i < n; i++) {scanf("%lld",&num[i]);}scanf("%s",order);for(int i=0;i<strlen(order);i++){if(order[i]=='L')locate=max(0ll,locate-1);else locate=min(n-1,locate+1);ans+=num[locate];}ans%=1000000007;printf("%lld", ans);return 0;
}

這道題就是需要簡單模擬一下就OK了：num數組用于記錄每一位分數，order數組用于記錄指令，locate用于記錄移動時候的所在坐標，關于如何處理到數組邊界0和n-1時，用函數max以及min即可（需要注意一個小細節，使用這倆個數學函數的時候，需要保證比較的倆個數類型相同，不能一個為int，另一個為long long，所以在max中寫0ll用于將默認的int強轉long long）。

3.小紅的素數合并

1.題目描述

2.輸入描述

3.輸出描述

4.示例

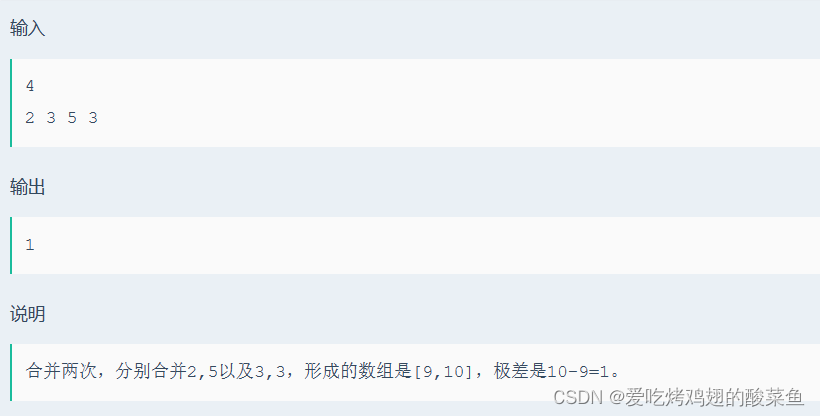
5.題解與思路

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;long long num[100005];
long long ans = 0, n = 0 ,mi = 1e18 ,ma = 0;
char order[100005];int main() {scanf("%lld",&n);for (int i = 0; i < n; i++) {scanf("%lld",&num[i]);}sort(num,num+n);int l=0 ,r=n-n%2-1;while(l<r){mi=min(mi,num[l]*num[r]);ma=max(ma,num[l]*num[r]);l++,r--;}if(n&1){mi=min(mi,num[n-1]);ma=max(ma,num[n-1]);}printf("%lld",ma-mi);return 0;
}

?先理解題意：素數先進行合并，最后尋找極差的最小值，在正式模擬之前我們需要明確一個問題，任意倆個素數想成合并后，一定是一個合數，合數不被作為接下來的合并對象。

明確這個問題后我們開始正是分析，何時相減為最小，即我們需要保證合成操作結束后合數的最大沒有那么大，最小沒有那么小，所以這道題我們的思路是先將數組的質數進行sort快排（從小到大），每一合并操作都將數組中第一項和最后一項進行合并，最后尋找極差。

另外還有一個需要注意的問題是，數組中質數的個數可能為奇也可能為偶，偶數個數的時候正常處理，奇數個數的時候我們需要在合成前舍棄一個數，又由題意可得尋找極差的最小，那我們直接舍棄數組中的最大值即可，代碼中是另外單開了一個if來處理奇數單獨與舍棄的數進行大小比較。

4.小紅的子序列求和

1.題目描述

2.輸入描述

3.輸出描述

4.示例

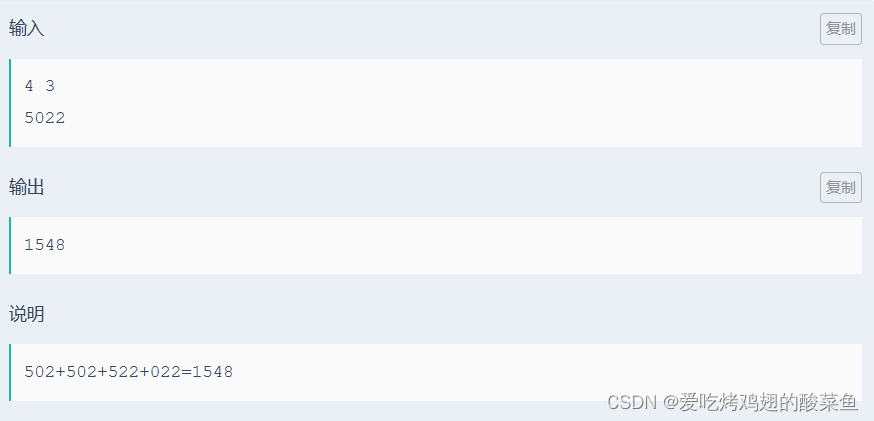
5.題解與思路

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;int n=0 ,k=0,ans=0;
int mod=1e9+7;
long long c[1010][1010];//預處理的楊輝三角
long long pow10[1010];//記錄不同位數的倍數
char num[1010];//記錄僅有數字組成的字符串int main(){//根據題意輸入scanf("%d%d",&n,&k);scanf("%s",num);//處理楊輝三角for(int i= 0;i<1000;i++){for(int j=0;j<=i;j++){if(j==0||i==j)c[i][j]=1;else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;}}//處理倍數pow10[0]=1;for(int i=1;i<1000;i++)pow10[i]=pow10[i-1]*10%mod;//關鍵模擬for(int i=0;i<n;i++){for(int j=0;j<k;j++){ans+=(num[i]-'0')*pow10[k-j-1]%mod*c[i][j]%mod*c[n-1-i][k-j-1]%mod;ans%=mod;}}printf("%d",ans);return 0;
} 

這道題我本人認為還是很有價值的（這道題可以用dp來做，但這里本人沒有使用這個方法），接下來將呈現我完整的思路歷程：

首先我們先對示例中的數據進行模擬

• 我們模擬的思路是以每一個數為基準，算出每一個數字在每一個不同的數中的“價值”，向前向后延展。
• 第一個數為5，5的前面沒有任何數，所以5只能做首位（這里說的都不是廢話，都是對分析有幫助的），因為k=3，所以我們需要在后面的022中任選倆個數，即C（3，2），又因為5在百位，所以5的價值為5*100*C（3，2）=1500。
• 第二個數為0。當取5時，后面就從22中任取其一，即C（2，1）；當不取5時，就將后面的22全取，即C（2，2）。所以0的價值為0*100*C（2，2）+0*10*C（2，1）=0。
• 第三個數為2。推理過程同理，第一個2的價值為2*1*C（2，2）+2*10*C（2，1）=42。
• 第四個數為2。推理過程同理，第二個2的價值為2*1*C（3，2）=6。
• 綜上，1500+0+42+6=1548，符合題意。

從特殊到一般，分析數據

• 我們發現每個數之前都有聯系，如C（3，2）=C（2，2）+C（2，1），這不禁可以讓你想到什么，這可就是大名鼎鼎楊輝三角啊，尋找每一位數字往前與往后所有的價值里面相乘的C(? ?,? ?)都和楊輝三角簡直如出一轍。
• 再處理好每位數字出現次數的問題，接下來要來解決所在位數的問題。這里我們創建了一個pow10數組用于記錄每個位數所包含的倍數。
• 處理完成后，我們接下來要通過代碼實現了。

代碼實現，有許多小細節以及需要分析的點

• 首先按照題目要求進行輸入。
• 接著提前處理楊輝三角并存儲進二維數組中。
• 接下來處理倍數，這些都是很基礎的操作。
• 最后正式模擬：注意在計算過程中要不斷的%1e9+7，防止溢出。先將著一位數字單獨拿出來（num[i]-'0'），乘以對應的倍數（如題目中的5作首位時，其為百位，即k-1-j=2，）乘以左側出現的次數c[i][j]，再乘以右側出現的次數c[n-1-i][k-j-1]（這里都可以拿5來舉例子，這里不再贅述），記得不斷取模就好。
• 最后輸出結果。

3.小結

今天的分享到這里就結束了，廢了好大功夫才將這兒四道題講的清晰明白，希望大家多多支持我哦~