Java常見數據結構---八大結構

??前言：

數據結構是計算機底層存儲、組織數據的方式。是指數據相互之間是以什么方式排列在一起的。通常情況下，精心選擇的數據結構可以帶來更高的運行或者存儲效率?

常見的八大數據結構：

?棧：

思想：

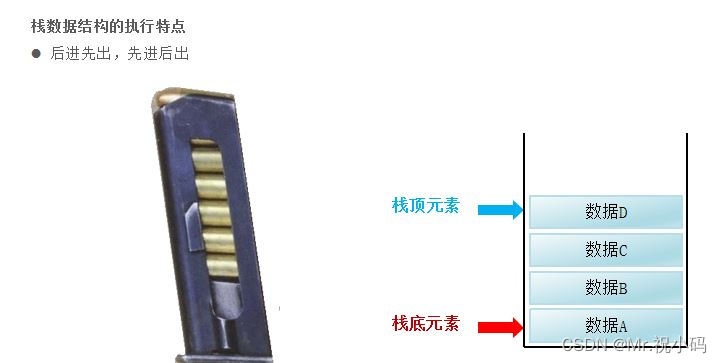
棧是一種數據結構，它遵循后進先出 (LIFO) 原則。這意味著最后添加的元素（稱為棧頂元素）將首先被移除。

特點：

**簡單性和效率：**棧的操作（push、pop、peek）可以在常數時間內完成。
**后進先出：**棧的 LIFO 特性使其非常適合需要按添加順序處理元素的應用。
可以理解為子彈夾一樣，先進后出，后出先進

?數據進入棧模型的過程稱為：壓/進棧

??數據出棧模型的過程稱為：彈/出棧

代碼：?

public class Stack {private int[] arr;private int top;private int capacity;public Stack(int capacity) {this.arr = new int[capacity];this.top = -1;this.capacity = capacity;}public void push(int element) {if (isFull()) {System.out.println("Stack overflow");return;}arr[++top] = element;}public int pop() {if (isEmpty()) {System.out.println("Stack underflow");return -1;}return arr[top--];}public int peek() {if (isEmpty()) {System.out.println("Stack is empty");return -1;}return arr[top];}public boolean isEmpty() {return top == -1;}public boolean isFull() {return top == capacity - 1;}public static void main(String[] args) {Stack stack = new Stack(5);stack.push(1);stack.push(2);stack.push(3);stack.push(4);System.out.println("Top element: " + stack.peek());stack.pop();stack.pop();System.out.println("Top element: " + stack.peek());}
}

過程：

過程解釋：

創建棧：我們創建一個容量為 5 的棧對象。棧是用數組實現的，其中?top?變量跟蹤棧頂元素的索引。
壓入元素：push?方法將元素壓入棧中。如果棧已滿，它會打印一條錯誤消息。
彈出元素：pop?方法從棧中移除并返回棧頂元素。如果棧為空，它會打印一條錯誤消息。
查看棧頂元素：peek?方法返回棧頂元素，但不將其移除。如果棧為空，它會打印一條錯誤消息。
檢查棧是否為空：isEmpty?方法檢查棧是否為空。
檢查棧是否已滿：isFull?方法檢查棧是否已滿。
主方法：**在主方法中，我們創建了一個棧對象，壓入一些元素，彈出一些元素，并打印棧頂元素。

?最后輸出：

Top element: 4

Top element: 2

隊列：

思想：

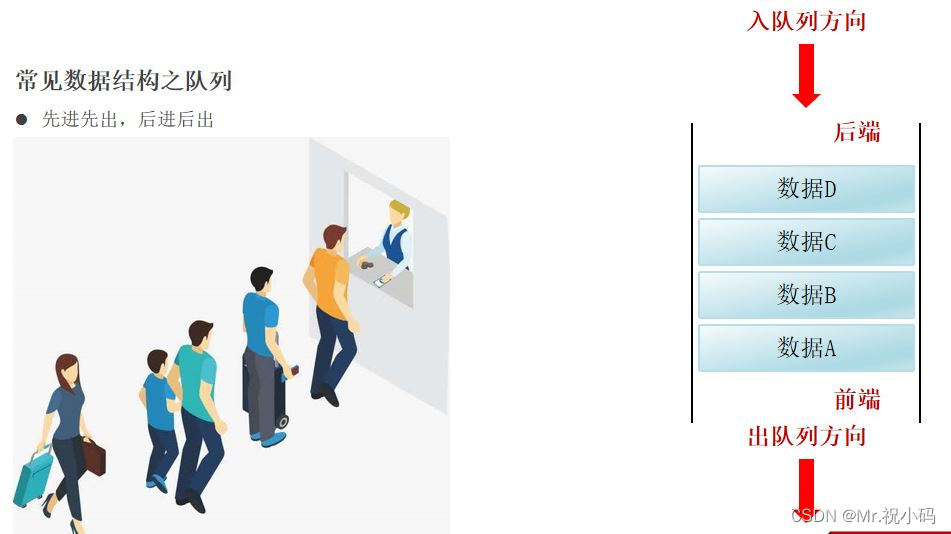
隊列是一種遵循先進先出 (FIFO) 原則的數據結構。這意味著隊列中的第一個添加的元素將首先被移除。與棧恰恰相反，隊列兩端全開，遵循先進先出，后進后出的原則

特點：

先進先出 (FIFO)：隊列遵循先進先出原則，這意味著第一個添加的元素將首先被移除。
線性數據結構：隊列是一種線性數據結構，這意味著元素按順序排列。
插入在末尾：新元素總是添加到隊列的末尾（也稱為尾部）。
刪除在頭部：元素從隊列的頭部（也稱為前端）移除。
限制訪問：隊列只允許在頭部和尾部進行插入和刪除操作。中間元素無法直接訪問。
隊列大小：隊列可以是固定大小的（使用數組實現）或動態大小的（使用鏈表實現）。
廣泛的應用：隊列在計算機科學中有廣泛的應用，例如消息傳遞、任務調度、緩沖和廣度優先搜索

代碼：?

import java.util.LinkedList;
import java.util.Queue;public class QueueExample {public static void main(String[] args) {// 創建一個隊列Queue<Integer> queue = new LinkedList<>();// 向隊列中添加元素queue.add(1);queue.add(2);queue.add(3);queue.add(4);// 從隊列中移除元素int removedElement = queue.remove(); // 移除并返回第一個元素// 查看隊列中的第一個元素int headElement = queue.peek(); // 返回第一個元素，但不將其移除// 檢查隊列是否為空boolean isEmpty = queue.isEmpty();// 打印隊列中的元素System.out.println("Queue elements: " + queue);// 打印移除的元素System.out.println("Removed element: " + removedElement);// 打印隊列頭部的元素System.out.println("Head element: " + headElement);// 打印隊列是否為空System.out.println("Queue is empty: " + isEmpty);}
}

輸出：

Queue elements: [2, 3, 4]
Removed element: 1
Head element: 2
Queue is empty: false

過程：?

創建隊列：我們使用 Java 的?LinkedList?類創建一個隊列。LinkedList 實現了 Queue 接口，它提供了隊列的基本操作。
添加元素：add?方法將元素添加到隊列的末尾。
移除元素：remove?方法從隊列中移除并返回第一個元素。
查看隊列頭部的元素：peek?方法返回隊列中的第一個元素，但不將其移除。
檢查隊列是否為空：isEmpty?方法檢查隊列是否為空。

數組：

思想：

數組是一種數據結構，它存儲固定數量的相同類型元素的集合。數組中的元素使用索引進行訪問，索引從 0 開始。

數組相對其他數據結構相對來說比較簡單理解，可以理解為是一組元素，起始值下標從0開始

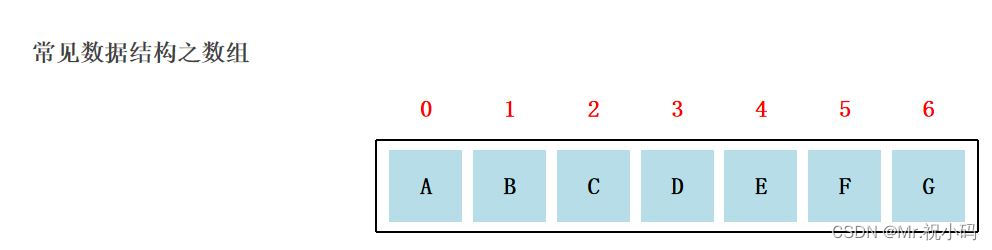
查詢速度快：查詢數據通過地址值和索引定位，查詢任意數據耗時相同。?
刪除效率低：要將原始數據刪除，同時后面每個數據前移。?

代碼：?

public class Array {public static void main(String[] args) {// 聲明一個長度為 7 的整型數組int[] arr = {1, 2, 3, 4, 5, 6, 7};// 遍歷數組并打印每個元素for (int element : arr) {System.out.println(element);}}
}

?過程：

聲明數組：我們聲明一個長度為 7 的整型數組，并使用花括號初始化其元素。
遍歷數組：使用增強 for 循環遍歷數組并打印每個元素。

鏈表：

思想：

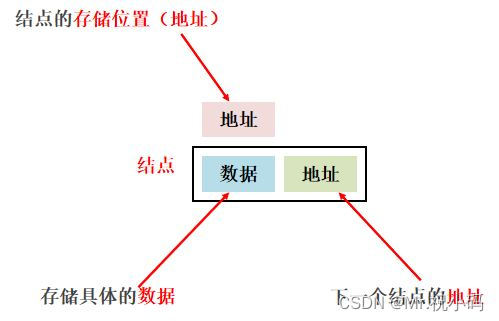
鏈表是一種數據結構，它由一組稱為節點的對象組成。每個節點包含一個數據項和指向下一個節點的引用。

在 Java 中，鏈表使用以下類實現：

LinkedList：一個雙向鏈表，允許在列表的任何位置添加和刪除元素。
ArrayList：一個基于數組的列表，在列表末尾添加和刪除元素非常高?

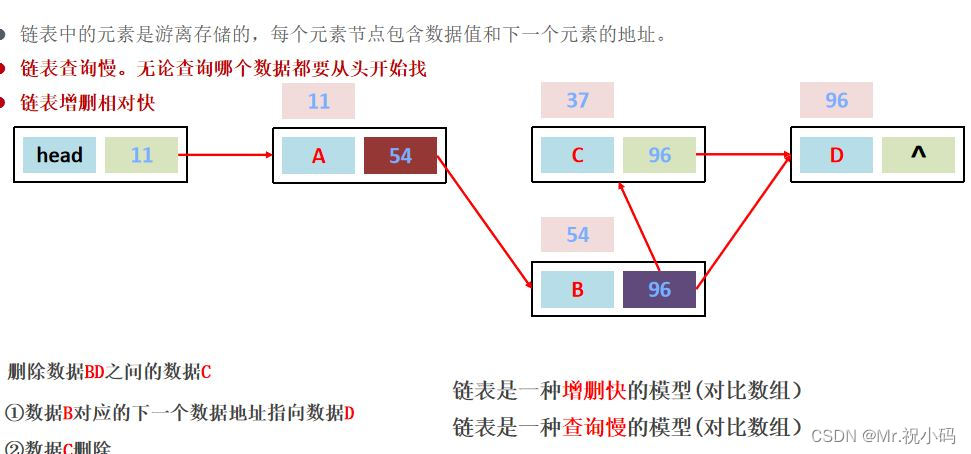
鏈表中的元素是游離存儲的，每個元素節點包含數據值和下一個元素的地址。?

鏈表是一種增刪快、查詢慢的模型(對比數組）

?代碼：

public class LinkedList {public static void main(String[] args) {// 創建一個鏈表LinkedList<String> list = new LinkedList<>();// 向鏈表中添加元素list.add("Apple");list.add("Banana");list.add("Orange");// 遍歷鏈表并打印每個元素for (String fruit : list) {System.out.println(fruit);}// 從鏈表中刪除元素list.remove("Banana");// 打印修改后的鏈表System.out.println("Modified list:");for (String fruit : list) {System.out.println(fruit);}}
}

輸出：

Modified list:Apple??Orange

Banana元素已經被鏈表刪除

二叉樹：

思想：

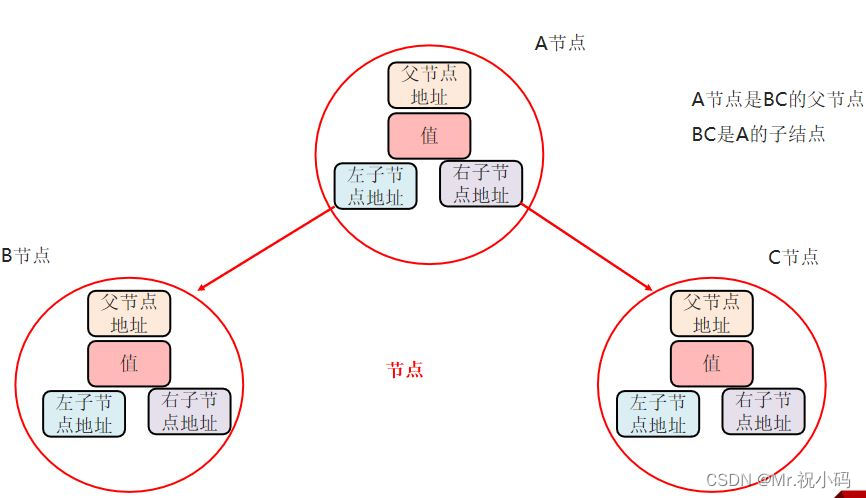
二叉樹（Binary tree）是樹形結構的一個重要類型。許多實際問題抽象出來的數據結構往往是二叉樹形式，即使是一般的樹也能簡單地轉換為二叉樹，而且二叉樹的存儲結構及其算法都較為簡單，因此二叉樹顯得特別重要。二叉樹特點是每個節點最多只能有兩棵子樹，且有左右之分?[1]。

特點：

?只能有一個根節點，每個節點最多支持2個直接子節點。

節點的度：節點擁有的子樹的個數，二叉樹的度不大于2 葉子節點度為0的節點，也稱之為終端結點。

高度：葉子結點的高度為1，葉子結點的父節點高度為2，以此類推，根節點的高度最高。

層：根節點在第一層，以此類推

兄弟節點：擁有共同父節點的節點互稱為兄弟節點

代碼：

public class BinaryTree {private Node root;public void add(int data) {root = addRecursive(root, data);}private Node addRecursive(Node current, int data) {if (current == null) {return new Node(data);}if (data < current.data) {current.left = addRecursive(current.left, data);} else if (data > current.data) {current.right = addRecursive(current.right, data);}return current;}public boolean contains(int data) {return containsRecursive(root, data);}private boolean containsRecursive(Node current, int data) {if (current == null) {return false;}if (data == current.data) {return true;} else if (data < current.data) {return containsRecursive(current.left, data);} else {return containsRecursive(current.right, data);}}public static void main(String[] args) {BinaryTree tree = new BinaryTree();tree.add(10);tree.add(5);tree.add(15);System.out.println("Contains 5: " + tree.contains(5));System.out.println("Contains 12: " + tree.contains(12));}
}class Node {int data;Node left;Node right;public Node(int data) {this.data = data;}
}

?過程：

添加元素：add()?方法使用遞歸將元素添加到二叉樹中。它將新元素與當前節點進行比較，并將其添加到左子樹或右子樹中，具體取決于元素的值。
查找元素：contains()?方法使用遞歸在二叉樹中查找元素。它將查找值與當前節點進行比較，并根據需要遞歸地遍歷左子樹或右子樹。
主方法：main()?方法創建二叉樹并向其中添加元素。然后，它調用?contains()?方法來查找樹中是否存在特定值。
輸出：Contains 5: true Contains 12: false

二叉查找樹：

思想：

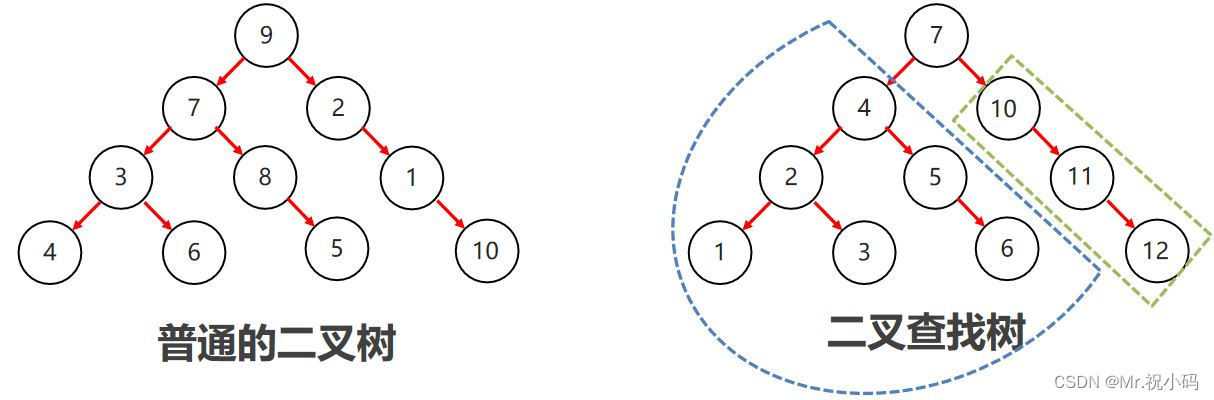
二叉搜索樹又被稱為排序樹，它或者是一顆空樹，或者是一棵具有以下性質的二叉樹：若它的左子樹不為空，則左子樹上所有節點的值都小于根節點的值若它的右子樹不為空，則右子樹上所有節點的值都大于根節點的值

?特點：

1，每一個節點上最多有兩個子節點

2，左子樹上所有節點的值都小于根節點的值

3，右子樹上所有節點的值都大于根節點的值?

目的：提高檢索數據的性能。

不同點：

二叉樹

每個節點最多有兩個子節點（左子節點和右子節點）。
沒有排序規則。
可以用于表示各種數據結構，例如堆和哈夫曼樹。

二叉搜索樹（BST）

一個特殊的二叉樹，其中每個節點的值都比其左子樹的所有值大，并且比其右子樹的所有值小。
具有以下性質：
- 左子樹中的所有值都小于根節點的值。
- 右子樹中的所有值都大于根節點的值。
- 左子樹和右子樹都是二叉搜索樹。

區別

二叉搜索樹和二叉樹之間的主要區別在于排序規則：

二叉樹沒有排序規則，而二叉搜索樹中的節點根據其值進行排序。

代碼：?

public class BinarySearchTree {private Node root;public void add(int data) {root = addRecursive(root, data);}private Node addRecursive(Node current, int data) {if (current == null) {return new Node(data);}if (data < current.data) {current.left = addRecursive(current.left, data);} else if (data > current.data) {current.right = addRecursive(current.right, data);}return current;}public boolean contains(int data) {return containsRecursive(root, data);}private boolean containsRecursive(Node current, int data) {if (current == null) {return false;}if (data == current.data) {return true;} else if (data < current.data) {return containsRecursive(current.left, data);} else {return containsRecursive(current.right, data);}}public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.add(10);tree.add(5);tree.add(15);System.out.println("Contains 5: " + tree.contains(5));System.out.println("Contains 12: " + tree.contains(12));}
}class Node {int data;Node left;Node right;public Node(int data) {this.data = data;}
}

?過程：

添加元素：add()?方法使用遞歸將元素添加到二叉查找樹中。它將新元素與當前節點進行比較，并將其添加到左子樹或右子樹中，具體取決于元素的值。
查找元素：contains()?方法使用遞歸在二叉查找樹中查找元素。它將查找值與當前節點進行比較，并根據需要遞歸地遍歷左子樹或右子樹。
主方法：main()?方法創建二叉查找樹并向其中添加元素。然后，它調用?contains()?方法來查找樹中是否存在特定值

輸出：

Contains 5: true
Contains 12: false

平衡二叉樹：

思想：

平衡二叉樹是一種特殊的二叉搜索樹，其中每個節點的左子樹和右子樹的高度差至多為 1。這確保了樹在很大程度上保持平衡，并且查找、插入和刪除操作的時間復雜度為 O(log n)，其中 n 是樹中的節點數。

?平衡二叉樹可以通過使用稱為旋轉的操作來實現。旋轉是重新排列樹中節點以維護平衡的一種方法。AVL 樹和紅黑樹使用不同的旋轉規則來保持平衡。

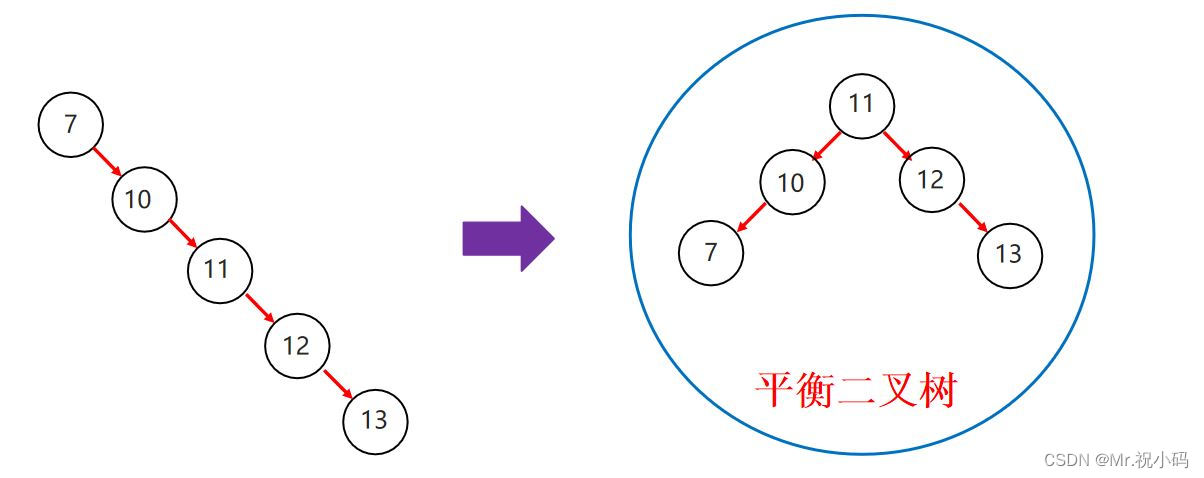
平衡二叉樹是在滿足查找二叉樹的大小規則下，讓樹盡可能矮小，以此提高查數據的性能。??

代碼：?

public class AVLTree {private Node root;public void add(int data) {root = addRecursive(root, data);}private Node addRecursive(Node current, int data) {if (current == null) {return new Node(data);}if (data < current.data) {current.left = addRecursive(current.left, data);} else if (data > current.data) {current.right = addRecursive(current.right, data);}updateHeight(current);return balance(current);}private Node balance(Node current) {int balanceFactor = getBalanceFactor(current);if (balanceFactor > 1) {if (getBalanceFactor(current.left) < 0) {current.left = leftRotate(current.left);}return rightRotate(current);} else if (balanceFactor < -1) {if (getBalanceFactor(current.right) > 0) {current.right = rightRotate(current.right);}return leftRotate(current);}return current;}private int getBalanceFactor(Node node) {if (node == null) {return 0;}return height(node.left) - height(node.right);}private int height(Node node) {if (node == null) {return 0;}return node.height;}private void updateHeight(Node node) {node.height = 1 + Math.max(height(node.left), height(node.right));}private Node leftRotate(Node node) {Node newRoot = node.right;node.right = newRoot.left;newRoot.left = node;updateHeight(node);updateHeight(newRoot);return newRoot;}private Node rightRotate(Node node) {Node newRoot = node.left;node.left = newRoot.right;newRoot.right = node;updateHeight(node);updateHeight(newRoot);return newRoot;}public static void main(String[] args) {AVLTree tree = new AVLTree();tree.add(10);tree.add(5);tree.add(15);System.out.println("Inorder traversal of the AVL tree:");inorderTraversal(tree.root);}private static void inorderTraversal(Node node) {if (node != null) {inorderTraversal(node.left);System.out.print(node.data + " ");inorderTraversal(node.right);}}
}class Node {int data;Node left;Node right;int height;public Node(int data) {this.data = data;this.height = 1;}
}

過程：?

添加元素：add()?方法使用遞歸將元素添加到 AVL 樹中。它將新元素與當前節點進行比較，并將其添加到左子樹或右子樹中，具體取決于元素的值。添加后，它更新節點的高度并平衡樹以保持 AVL 性質。
平衡樹：balance()?方法檢查節點的平衡因子并執行必要的旋轉以平衡樹。
獲取平衡因子：getBalanceFactor()?方法計算節點的平衡因子，它等于左子樹的高度減去右子樹的高度。
獲取高度：height()?方法計算節點的高度，它等于其子樹中最大高度加 1。
更新高度：updateHeight()?方法更新節點的高度，它等于其子樹中最大高度加 1。
左旋轉：leftRotate()?方法執行左旋轉操作，它將當前節點的右子樹作為新根，并將當前節點作為新根的左子樹。
右旋轉：rightRotate()?方法執行右旋轉操作，它將當前節點的左子樹作為新根，并將當前節點作為新根的右子樹。
主方法：main()?方法創建 AVL 樹并向其中添加元素。然后，它打印樹的中序遍歷以顯示樹的順序。

結果：?

Inorder traversal of the AVL tree:
5 10 15
?

紅黑樹：

規則：?

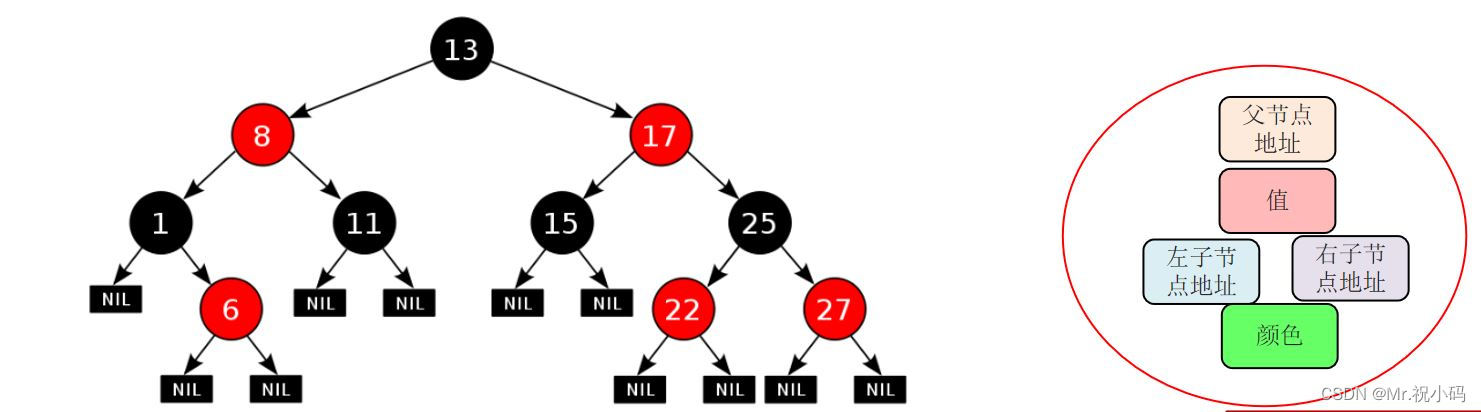
?每一個節點或是紅色的，或者是黑色的，根節點必須是黑色。

如果某一個節點是紅色，那么它的子節點必須是黑色(不能出現兩個紅色節點相連的情況)。

對每一個節點，從該節點到其所有后代葉節點的簡單路徑上，均包含相同數目的黑色節點。

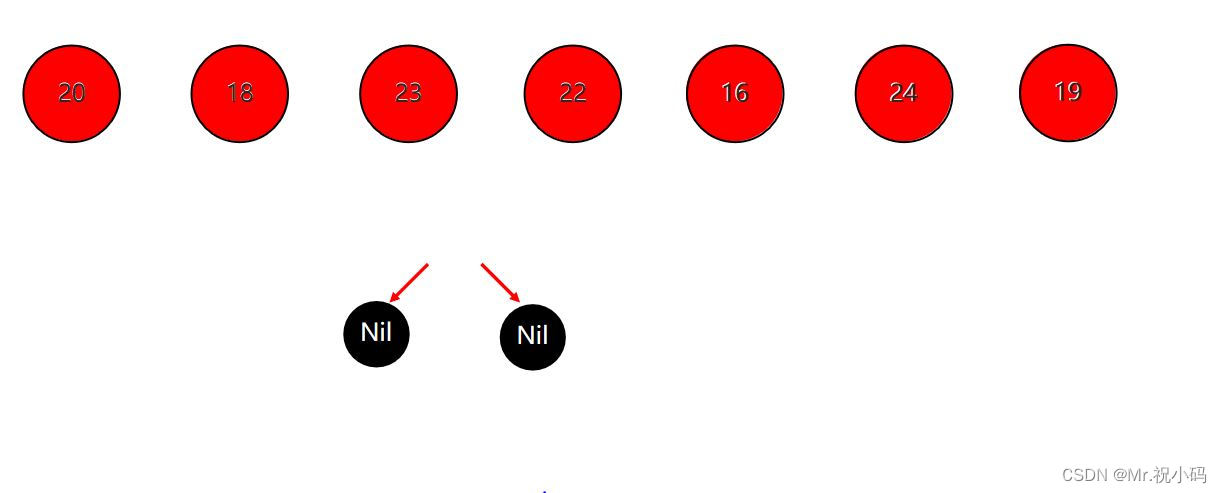
當添加的節點為根節點時，直接變成黑色就可以了?

?代碼：

import java.util.ArrayList;
import java.util.List;public class RedBlackTree {private Node root;public void add(int data) {root = addRecursive(root, data);root.color = Color.BLACK;}private Node addRecursive(Node current, int data) {if (current == null) {return new Node(data);}if (data < current.data) {current.left = addRecursive(current.left, data);} else if (data > current.data) {current.right = addRecursive(current.right, data);}if (isRed(current.left) && isRed(current.right)) {flipColors(current);}if (isRed(current.left) && isRed(current.left.left)) {current = rightRotate(current);}if (isRed(current.right) && isRed(current.right.right)) {current = leftRotate(current);}return current;}private void flipColors(Node node) {node.color = Color.RED;node.left.color = Color.BLACK;node.right.color = Color.BLACK;}private Node rightRotate(Node node) {Node newRoot = node.left;node.left = newRoot.right;newRoot.right = node;newRoot.color = node.color;node.color = Color.RED;return newRoot;}private Node leftRotate(Node node) {Node newRoot = node.right;node.right = newRoot.left;newRoot.left = node;newRoot.color = node.color;node.color = Color.RED;return newRoot;}private boolean isRed(Node node) {return node != null && node.color == Color.RED;}public static void main(String[] args) {RedBlackTree tree = new RedBlackTree();int[] data = {20, 18, 23, 20, 16, 24, 19};for (int value : data) {tree.add(value);}List<Node> redNodes = new ArrayList<>();inorderTraversal(tree.root, redNodes);System.out.println("Red nodes in the Red-Black tree:");for (Node node : redNodes) {System.out.print(node.data + " ");}}private static void inorderTraversal(Node node, List<Node> redNodes) {if (node != null) {inorderTraversal(node.left, redNodes);if (node.color == Color.RED) {redNodes.add(node);}inorderTraversal(node.right, redNodes);}}private enum Color {RED,BLACK}private static class Node {int data;Node left;Node right;Color color;public Node(int data) {this.data = data;this.color = Color.RED;}}
}