動態規劃在子數組/子串問題

一、最大子數組和（LeetCode 53）

二、環形子數組的最大和（LeetCode 918）

三、乘積最大子數組（LeetCode 152）

四、乘積為正數的最長子數組長度（LeetCode 1567）

五、等差數列劃分（LeetCode 413）

六、最長湍流子數組（LeetCode 978）

七、單詞拆分（LeetCode 139）

?八、環繞字符串中唯一的子字符串（LeetCode 467）

總結

動態規劃（Dynamic Programming，簡稱 DP）是解決多階段決策問題的有效方法，尤其在處理子數組、子串相關問題時，能通過狀態定義和轉移，高效找到最優解。下面結合幾道經典題目，分享動態規劃在這類問題中的分析方法與思路。
?

一、最大子數組和（LeetCode 53）

?
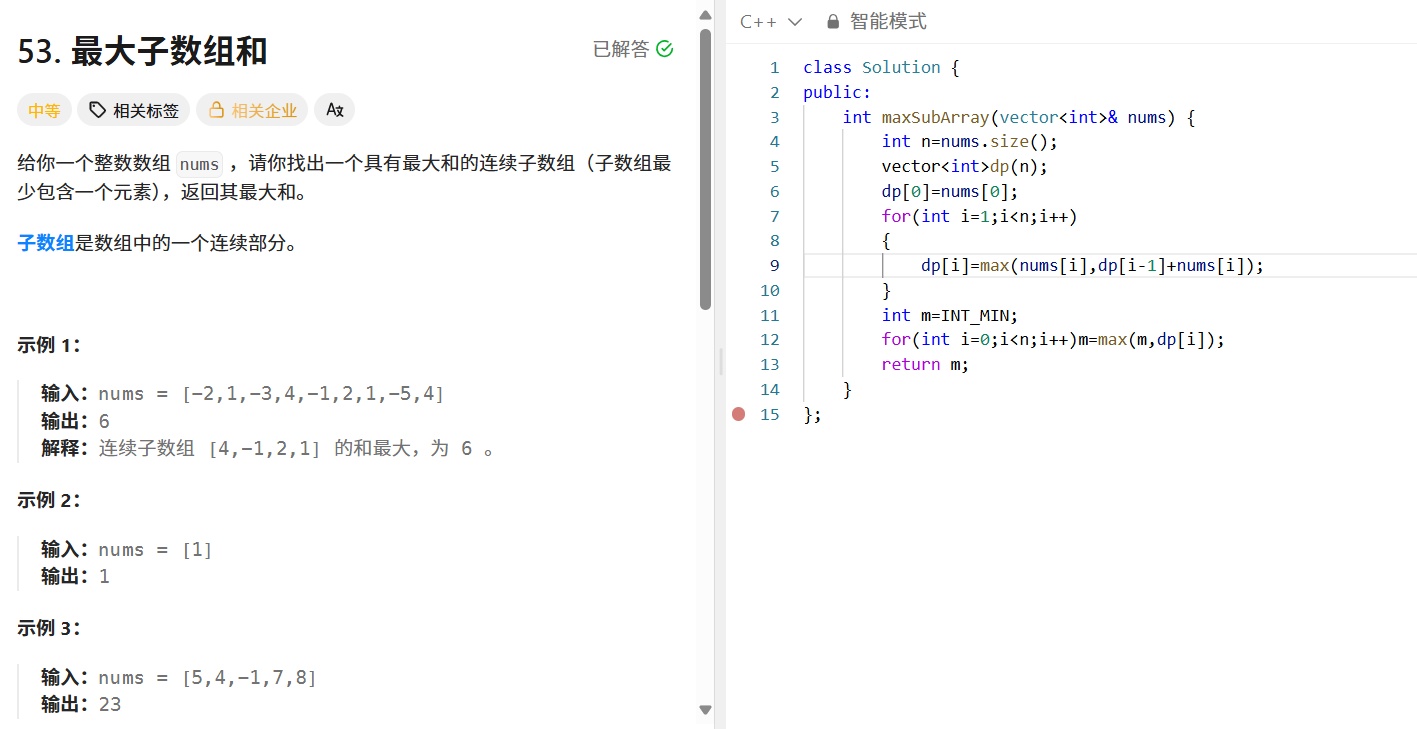
問題描述
?
給定整數數組 ?nums?，找出和最大的連續子數組，返回其最大和。
?
分析思路
?
- 狀態定義：?dp[i]??表示以 ?nums[i]??結尾的連續子數組的最大和。
- 狀態轉移：對于 ?nums[i]?，有兩種選擇，要么加入前面的子數組（?dp[i - 1] + nums[i]?），要么自己作為新子數組的起點（?nums[i]?），取兩者最大值，即 ?dp[i] = max(nums[i], dp[i - 1] + nums[i])?。
- 初始條件：?dp[0] = nums[0]?，因為第一個元素自己就是一個子數組。
- 結果提取：遍歷 ?dp??數組，找到最大值。
?
代碼實現
?

class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n);dp[0] = nums[0];for (int i = 1; i < n; i++) {dp[i] = max(nums[i], dp[i - 1] + nums[i]);}int maxSum = INT_MIN;for (int num : dp) {maxSum = max(maxSum, num);}return maxSum;}
};

二、環形子數組的最大和（LeetCode 918）

?
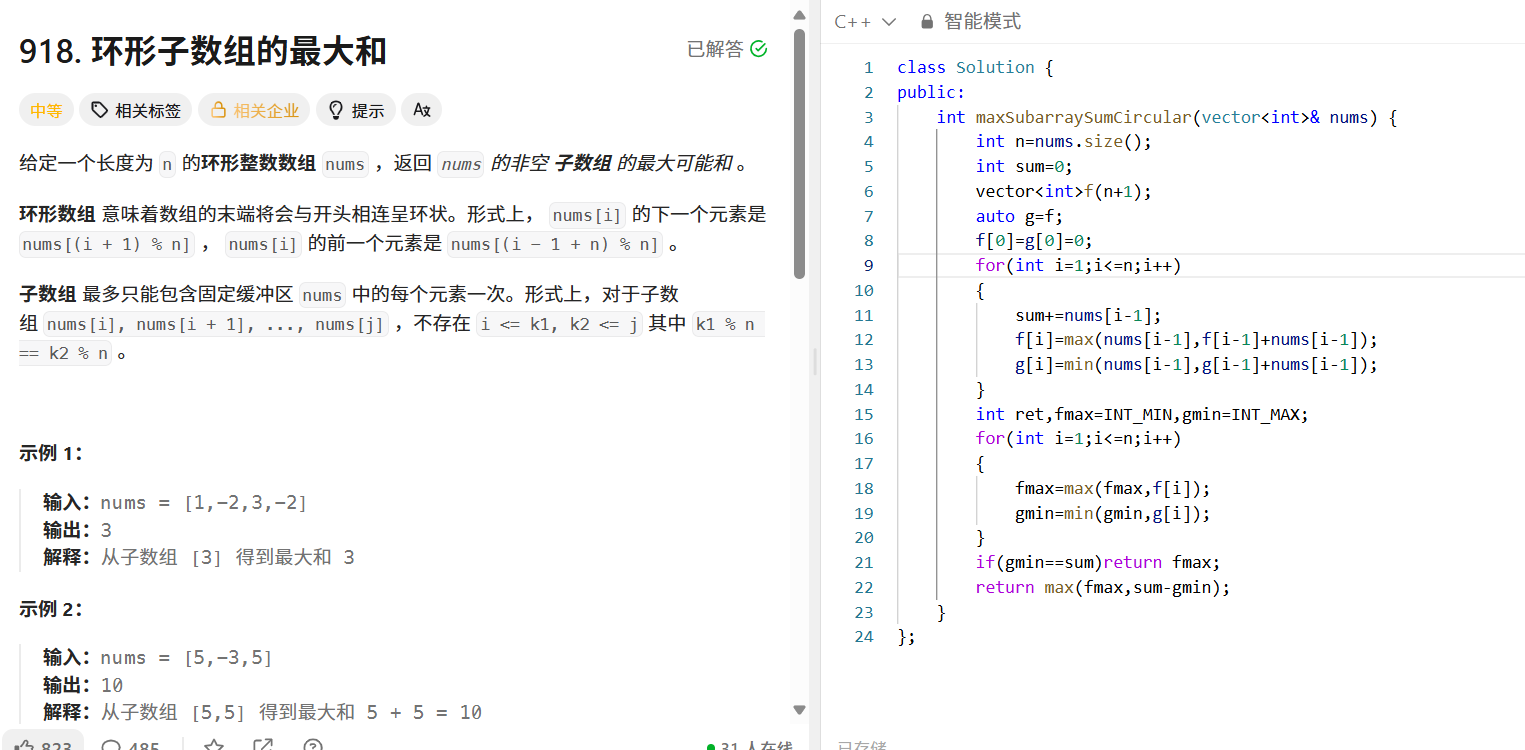
問題描述
?
給定環形整數數組 ?nums?，返回非空子數組的最大可能和（環形意味著數組末端與開頭相連）。
?
分析思路
?
環形子數組的最大和有兩種情況：
?
- 情況一：最大和子數組在數組內部（非環形），可通過常規最大子數組和方法計算。
- 情況二：最大和子數組跨越數組首尾（環形），此時最大和等于數組總和減去內部最小子數組和。
需要注意，若數組所有元素都是負數，此時總和減去最小子數組和（也是負數）會得到錯誤結果，需單獨判斷。
?
代碼實現

class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();int sum = 0;vector<int> f(n + 1);auto g = f;f[0] = g[0] = 0;for (int i = 1; i <= n; i++) {sum += nums[i - 1];f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);}int fmax = INT_MIN, gmin = INT_MAX;for (int i = 1; i <= n; i++) {fmax = max(fmax, f[i]);gmin = min(gmin, g[i]);}if (gmin == sum) return fmax;return max(fmax, sum - gmin);}
};

三、乘積最大子數組（LeetCode 152）

?
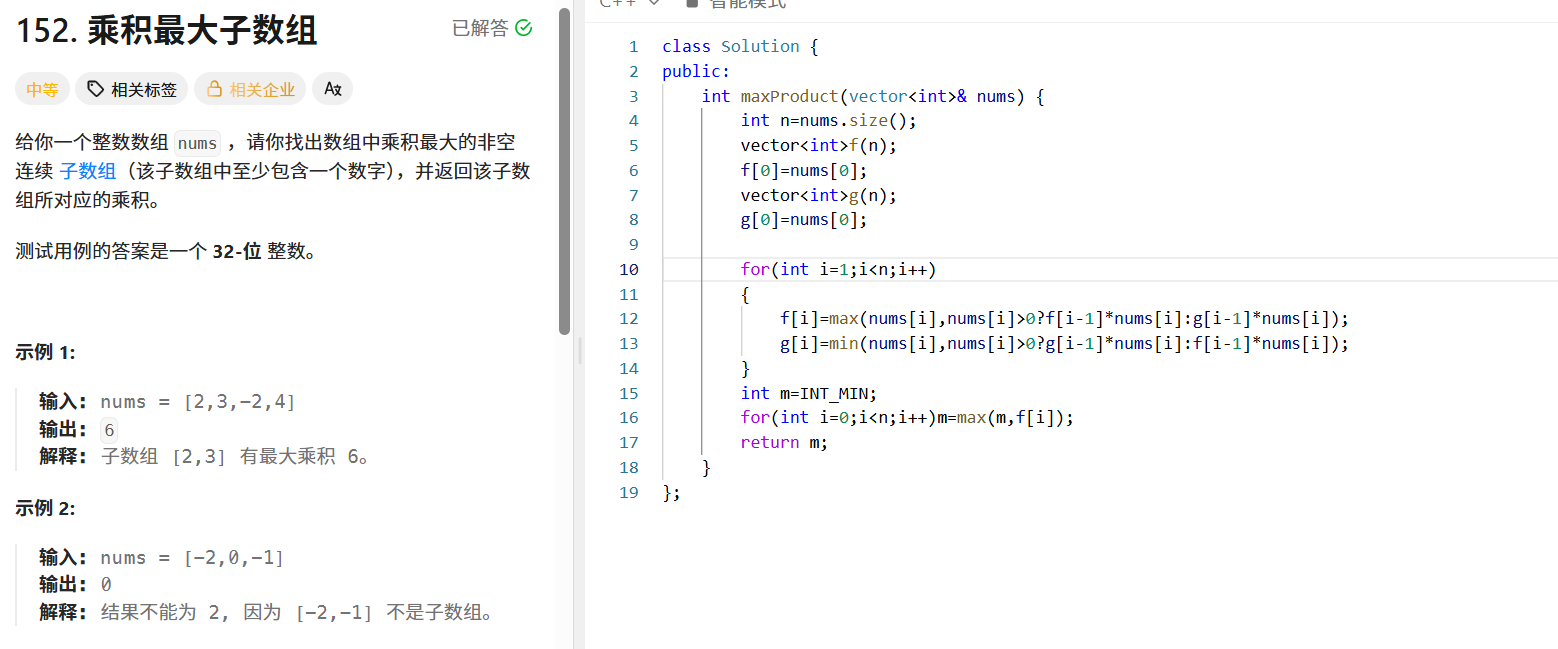
問題描述
?
給定整數數組 ?nums?，找出乘積最大的非空連續子數組，返回該乘積。
?
分析思路
?
由于乘法的特殊性，負數相乘可能得到正數，所以需要同時記錄以 ?nums[i]??結尾的子數組的最大乘積和最小乘積。
?
- 狀態定義：?f[i]??表示以 ?nums[i]??結尾的子數組的最大乘積，?g[i]??表示以 ?nums[i]??結尾的子數組的最小乘積。
- 狀態轉移：根據 ?nums[i]??的正負，選擇與 ?f[i - 1]??或 ?g[i - 1]??相乘，即：
- 若 ?nums[i] > 0?，?f[i] = max(nums[i], f[i - 1] * nums[i])?，?g[i] = min(nums[i], g[i - 1] * nums[i])?；
- 若 ?nums[i] < 0?，?f[i] = max(nums[i], g[i - 1] * nums[i])?，?g[i] = min(nums[i], f[i - 1] * nums[i])?；
- 若 ?nums[i] == 0?，?f[i] = g[i] = 0?。
- 初始條件：?f[0] = g[0] = nums[0]?。
- 結果提取：遍歷 ?f??數組，找到最大值。
?
代碼實現

class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n);f[0] = nums[0];vector<int> g(n);g[0] = nums[0];for (int i = 1; i < n; i++) {if (nums[i] > 0) {f[i] = max(nums[i], f[i - 1] * nums[i]);g[i] = min(nums[i], g[i - 1] * nums[i]);} else if (nums[i] < 0) {f[i] = max(nums[i], g[i - 1] * nums[i]);g[i] = min(nums[i], f[i - 1] * nums[i]);} else {f[i] = g[i] = 0;}}int maxProd = INT_MIN;for (int num : f) {maxProd = max(maxProd, num);}return maxProd;}
};

四、乘積為正數的最長子數組長度（LeetCode 1567）

?
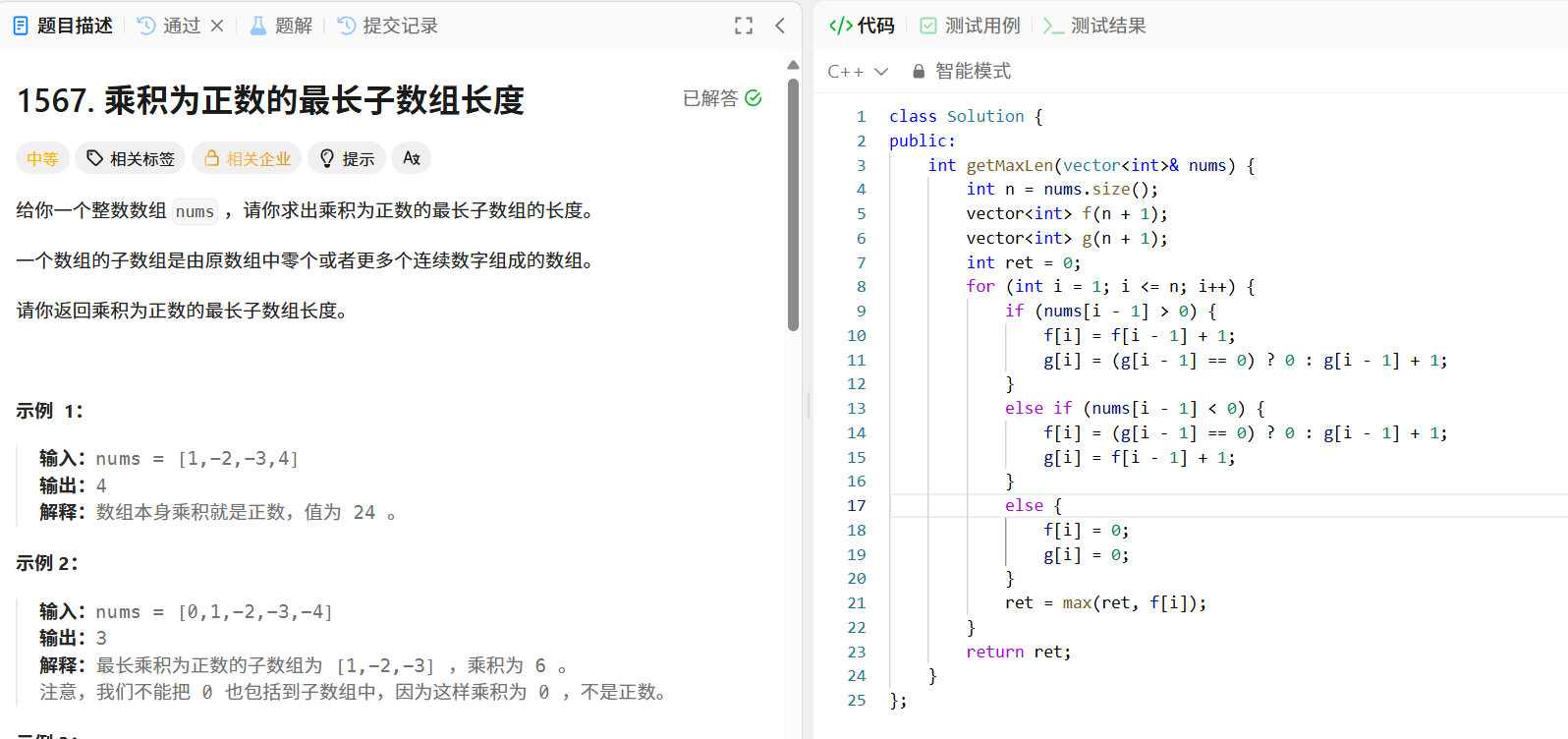
問題描述
?
給定整數數組 ?nums?，求出乘積為正數的最長子數組的長度。
?
分析思路
?
- 狀態定義：?f[i]??表示以 ?nums[i - 1]??結尾的乘積為正數的最長子數組長度，?g[i]??表示以 ?nums[i - 1]??結尾的乘積為負數的最長子數組長度。
- 狀態轉移：根據 ?nums[i - 1]??的正負進行轉移：
- 若 ?nums[i - 1] > 0?，?f[i] = f[i - 1] + 1?，?g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1?；
- 若 ?nums[i - 1] < 0?，?f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1?，?g[i] = f[i - 1] + 1?；
- 若 ?nums[i - 1] == 0?，?f[i] = g[i] = 0?。
- 初始條件：?f[0] = g[0] = 0?。
- 結果提取：遍歷過程中記錄 ?f[i]??的最大值。
?
代碼實現
?

class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);vector<int> g(n + 1);int ret = 0;for (int i = 1; i <= n; i++) {if (nums[i - 1] > 0) {f[i] = f[i - 1] + 1;g[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;} else if (nums[i - 1] < 0) {f[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;} else {f[i] = 0;g[i] = 0;}ret = max(ret, f[i]);}return ret;}
};

五、等差數列劃分（LeetCode 413）

?
問題描述
?
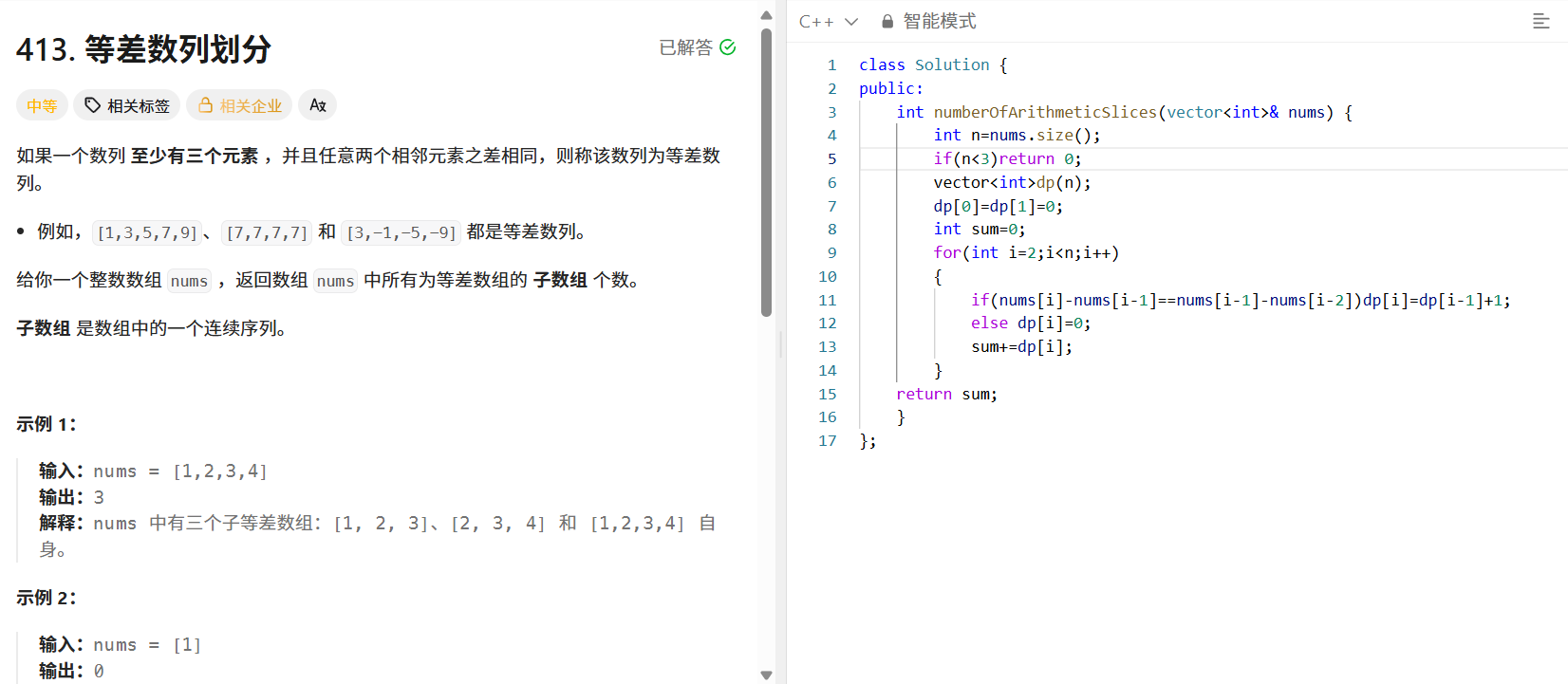
如果一個數列至少有三個元素，且任意兩個相鄰元素之差相同，則稱該數列為等差數列。給定整數數組 ?nums?，返回數組中所有為等差數組的子數組個數。
?
分析思路
?
- 狀態定義：?dp[i]??表示以 ?nums[i]??結尾的等差數列的個數。
- 狀態轉移：若 ?nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]?，說明以 ?nums[i]??結尾能形成新的等差數列，?dp[i] = dp[i - 1] + 1?；否則 ?dp[i] = 0?。
- 初始條件：?dp[0] = dp[1] = 0?，因為前兩個元素無法形成至少三個元素的等差數列。
- 結果提取：將所有 ?dp[i]??相加，得到總的等差數列子數組個數。
?
代碼實現

??
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3) return 0;vector<int> dp(n);dp[0] = dp[1] = 0;int sum = 0;for (int i = 2; i < n; i++) {if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {dp[i] = dp[i - 1] + 1;} else {dp[i] = 0;}sum += dp[i];}return sum;}
};

六、最長湍流子數組（LeetCode 978）

?
問題描述
?
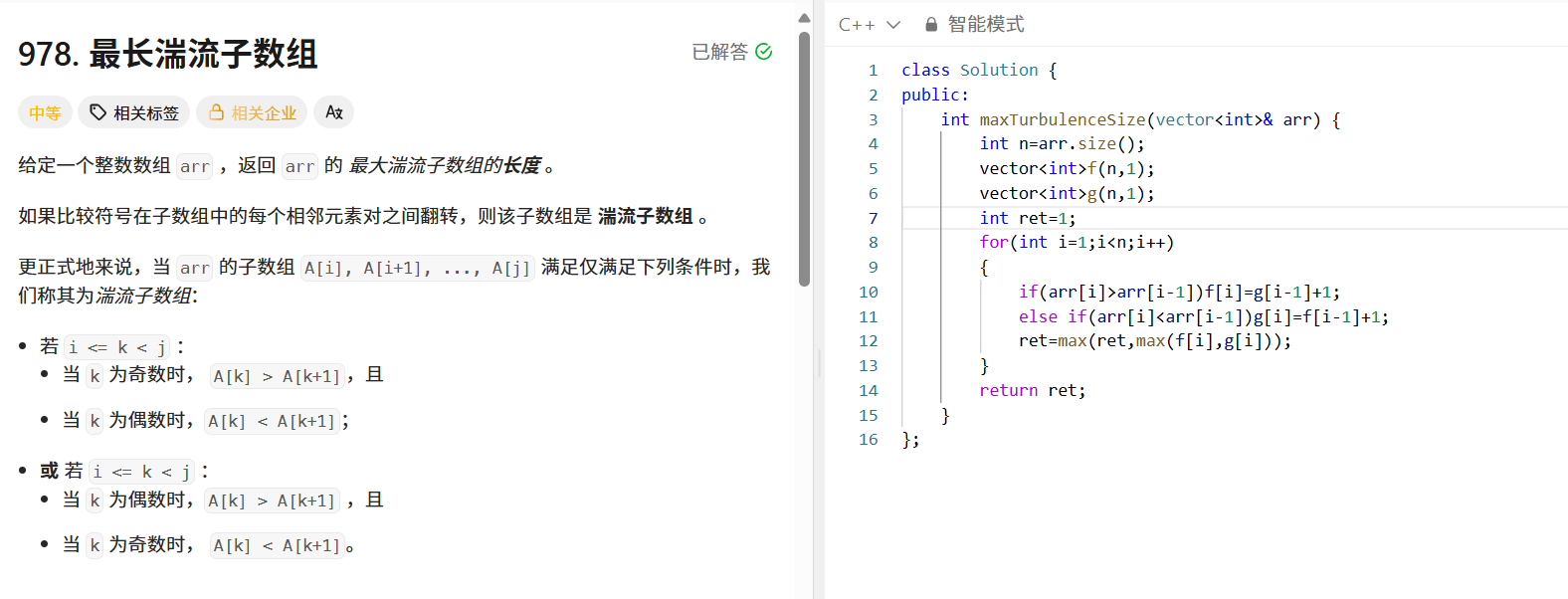
給定整數數組 ?arr?，返回其最大湍流子數組的長度。湍流子數組是指相鄰元素對之間比較符號翻轉的子數組。
?
分析思路
?
- 狀態定義：?f[i]??表示以 ?arr[i]??結尾，且最后是上升（?arr[i] > arr[i - 1]?）的湍流子數組長度；?g[i]??表示以 ?arr[i]??結尾，且最后是下降（?arr[i] < arr[i - 1]?）的湍流子數組長度。
- 狀態轉移：
- 若 ?arr[i] > arr[i - 1]?，?f[i] = g[i - 1] + 1?，?g[i] = 1?；
- 若 ?arr[i] < arr[i - 1]?，?g[i] = f[i - 1] + 1?，?f[i] = 1?；
- 若 ?arr[i] == arr[i - 1]?，?f[i] = g[i] = 1?。
- 初始條件：?f[0] = g[0] = 1?，單個元素自身是長度為 1 的湍流子數組。
- 結果提取：遍歷過程中記錄 ?f[i]??和 ?g[i]??中的最大值。
?
代碼實現

??
class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n, 1);vector<int> g(n, 1);int ret = 1;for (int i = 1; i < n; i++) {if (arr[i] > arr[i - 1]) {f[i] = g[i - 1] + 1;g[i] = 1;} else if (arr[i] < arr[i - 1]) {g[i] = f[i - 1] + 1;f[i] = 1;} else {f[i] = g[i] = 1;}ret = max(ret, max(f[i], g[i]));}return ret;}
};

七、單詞拆分（LeetCode 139）

?
問題描述
?
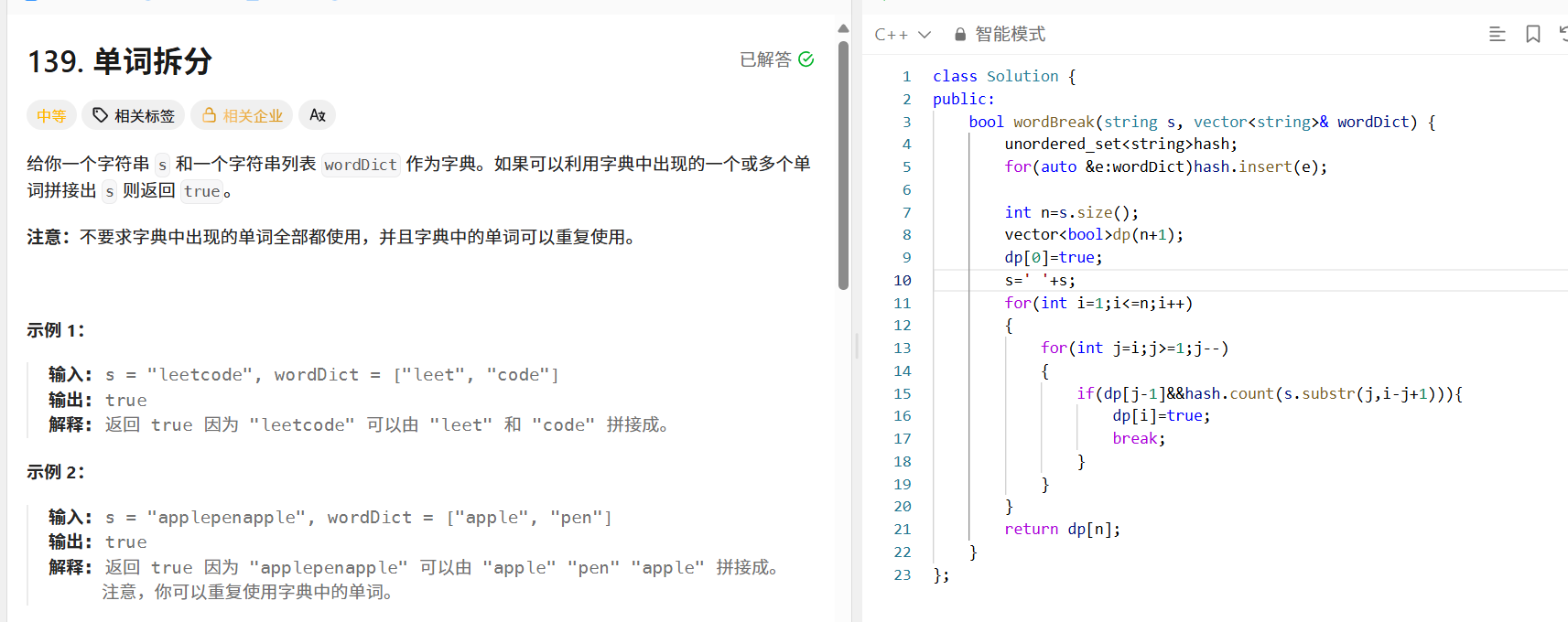
給定字符串 ?s??和字符串列表 ?wordDict??作為字典，判斷是否可以利用字典中出現的一個或多個單詞拼接出 ?s?。
?
分析思路
?
- 狀態定義：?dp[i]??表示字符串 ?s??的前 ?i??個字符是否能被字典拼接而成。
- 狀態轉移：對于每個 ?i?，枚舉分割點 ?j?（從 ?i??到 ?1?），若 ?dp[j - 1]??為 ?true?（前 ?j - 1??個字符能被拼接）且 ?s??的 ?j??到 ?i??子串在字典中，則 ?dp[i] = true?。
- 初始條件：?dp[0] = true?，空字符串能被拼接。
- 結果提取：?dp[s.size()]??即為最終結果，表示整個字符串是否能被拼接。
?
代碼實現

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> hash;for (auto &e : wordDict) hash.insert(e);int n = s.size();vector<bool> dp(n + 1);dp[0] = true;s = " " + s;for (int i = 1; i <= n; i++) {for (int j = i; j >= 1; j--) {if (dp[j - 1] && hash.count(s.substr(j, i - j + 1))) {dp[i] = true;break;}}}return dp[n];}
};

?八、環繞字符串中唯一的子字符串（LeetCode 467）

?
問題描述
?
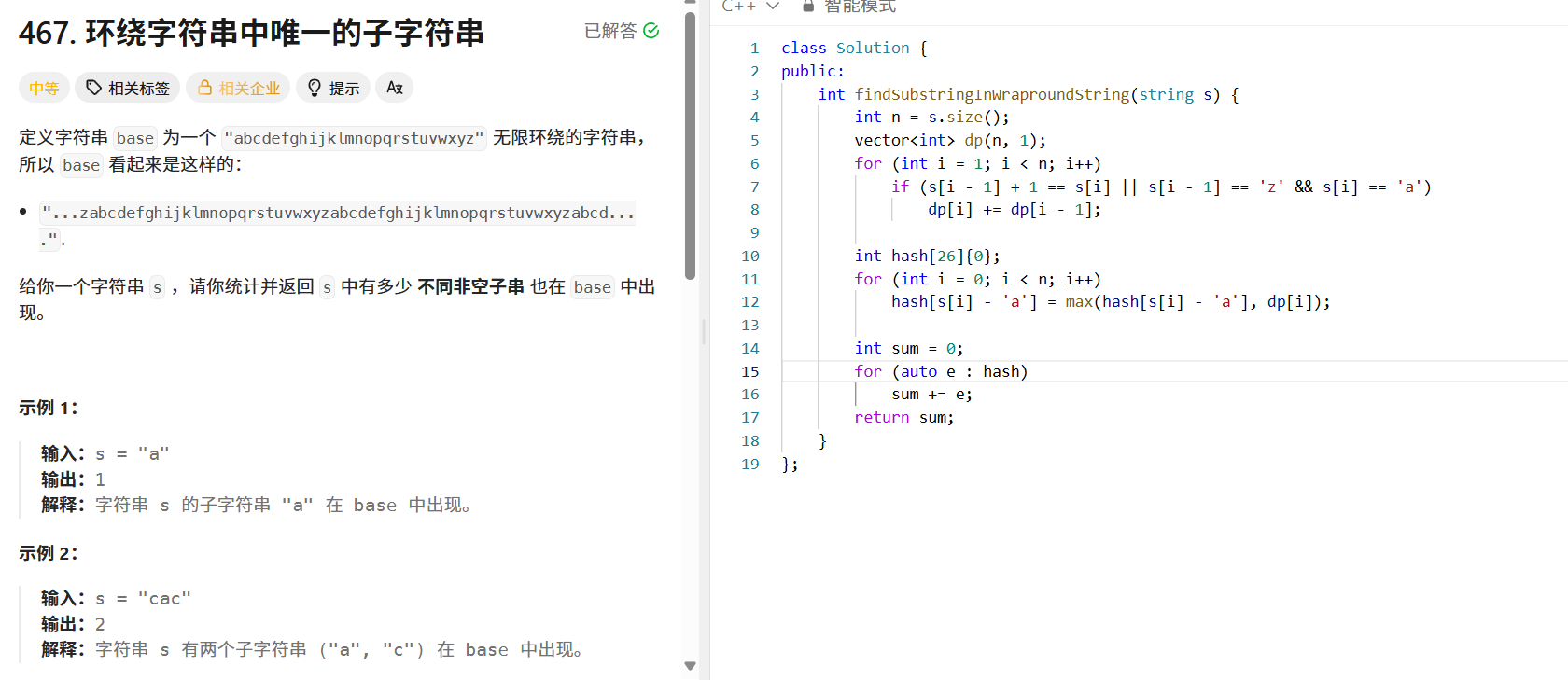
定義字符串 ?base??為 ?"abcdefghijklmnopqrstuvwxyz"??無限環繞的字符串，給定字符串 ?s?，統計并返回 ?s??中有多少不同非空子串也在 ?base??中出現。
?
分析思路
?
- 狀態定義：?dp[i]??表示以 ?s[i]??結尾的符合 ?base??規律的子串長度。
- 狀態轉移：若 ?s[i - 1]??到 ?s[i]??符合 ?base??的連續規律（如 ?s[i - 1]??是 ?'z'??且 ?s[i]??是 ?'a'?，或 ?s[i] = s[i - 1] + 1?），則 ?dp[i] = dp[i - 1] + 1?；否則 ?dp[i] = 1?。
- 去重處理：用長度為 26 的數組 ?hash??記錄每個字符結尾的最長符合規律子串長度，最后將所有 ?hash??元素相加，得到不同子串的個數（因為最長長度包含了所有更短的以該字符結尾的符合規律子串）。
?
代碼實現
???

class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();vector<int> dp(n, 1);for (int i = 1; i < n; i++) {if (s[i - 1] + 1 == s[i] || (s[i - 1] == 'z' && s[i] == 'a')) {dp[i] += dp[i - 1];}}int hash[26] = {0};for (int i = 0; i < n; i++) {hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);}int sum = 0;for (auto e : hash) {sum += e;}return sum;}
};