AVL樹

概念性質

一顆AVL樹或是空樹，或者具有一下性質的二叉搜索樹：左右都是AVL樹，左右子樹高度差的絕對值不超過1

AVL樹有n個結果，高度保持在O（logN） 搜索時間復雜度O(logN）

模擬實現插入

定義：左子樹，右子樹，父親節點，自身值，平衡因子

static class TreeNode{public TreeNode left;public TreeNode right;public TreeNode parent;public int val;public int bf;//平衡因子public TreeNode(int val) {this.val = val;}}

插入

1.先將數據插入AVL樹中（和二叉搜索樹一樣）

  public static boolean insert(int val){TreeNode node=new TreeNode(val);if(root==null){root=node;return true;}TreeNode cur=root;TreeNode parent=null;while(cur!=null){if(cur.val==val){return false;}else if(cur.val>val){parent=cur;cur=cur.left;}else{parent=cur;cur=cur.right;}}//cur=nullif(parent.val>val){parent.left=node;}else{parent.right=node;}node.parent=parent;cur=node;//調整平衡因子while(parent!=null){if(cur==parent.left){parent.bf--;}else{parent.bf++;}if(parent.bf==0){break;}else if(parent.bf==1||parent.bf==-1){//繼續向上調整cur=parent;parent=cur.parent;}else{if(parent.bf==2){//右樹高度高if(cur.bf==1){rotateLeft(parent);}else{rotateRL(parent);}}else{if(cur.bf==-1){rotateRight(parent);}else{rotateLR(parent);}}}}return  true;}

2.插入后，根據平衡因子進行調整

當parent.bf==0時就平衡了，不需要再向上調整了

旋轉

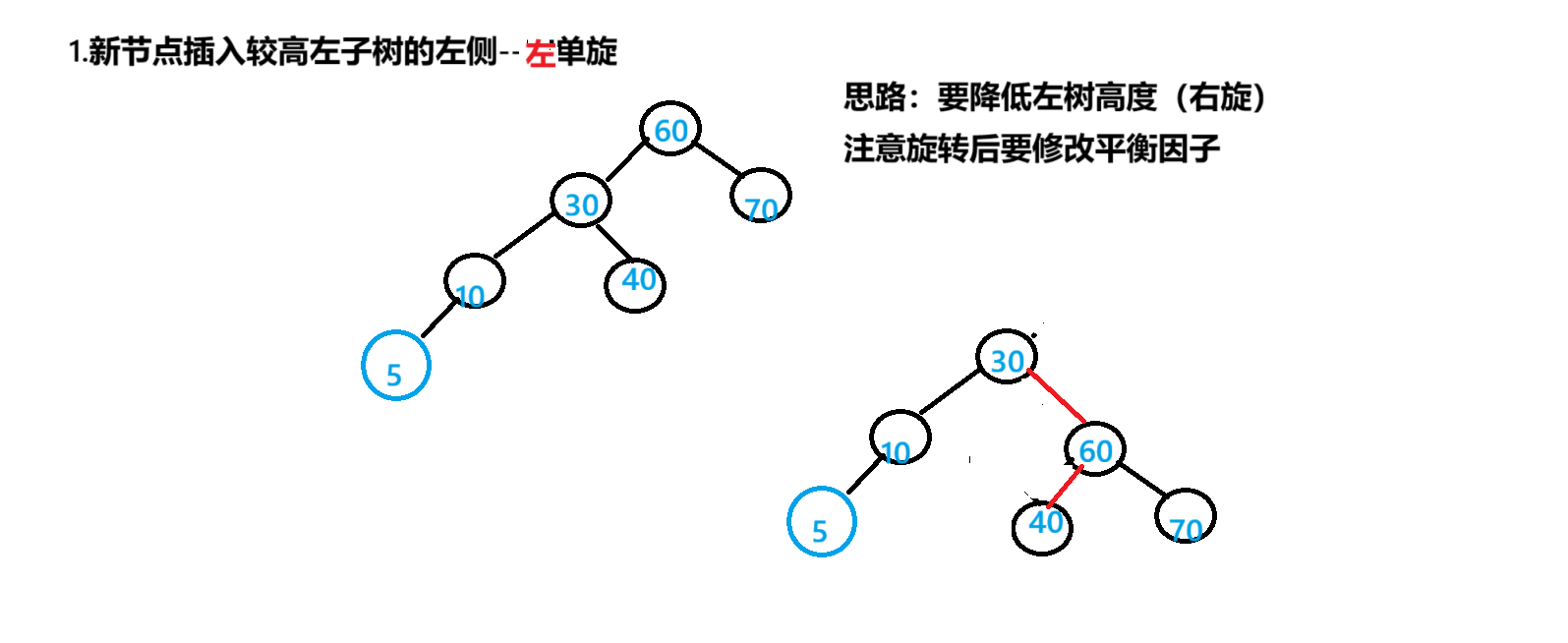
private static void rotateLeft(TreeNode parent) {TreeNode subR=parent.right;TreeNode subRL=subR.left;parent.right=subRL;if(subRL!=null){subRL.parent=parent;}TreeNode pParent=parent.parent;parent.parent=subR;if(parent==root){root=subR;subR.parent=null;}else{if(pParent.left==parent){pParent.left=subR;}else{pParent.right=subR;}subR.parent=pParent;}subR.bf=parent.bf=0;}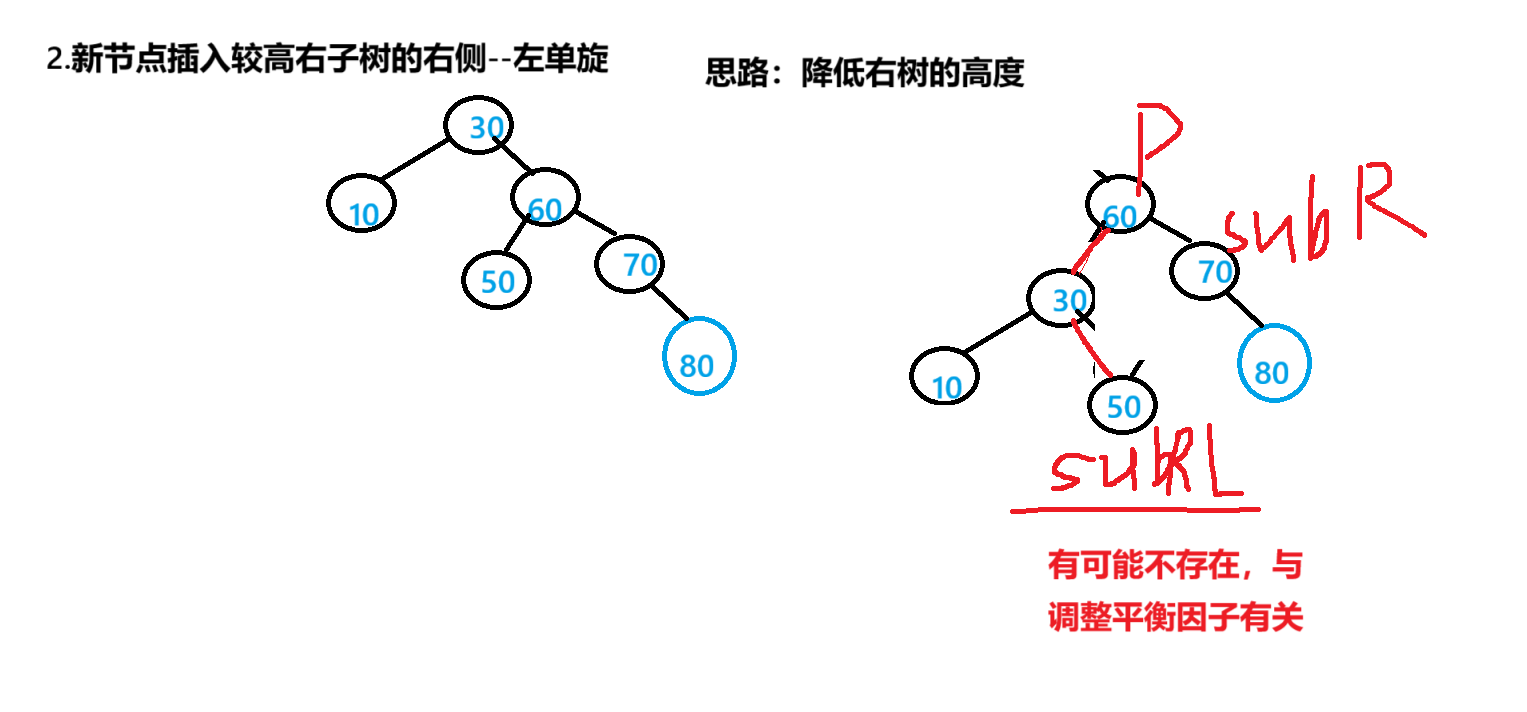

 private static void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;//沒有subLRif(subLR != null) {subLR.parent = parent;}//必須先記錄TreeNode pParent = parent.parent;parent.parent = subL;//檢查 當前是不是就是根節點if(parent == root) {root = subL;root.parent = null;}else {//不是根節點，判斷這棵子樹是左子樹還是右子樹if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}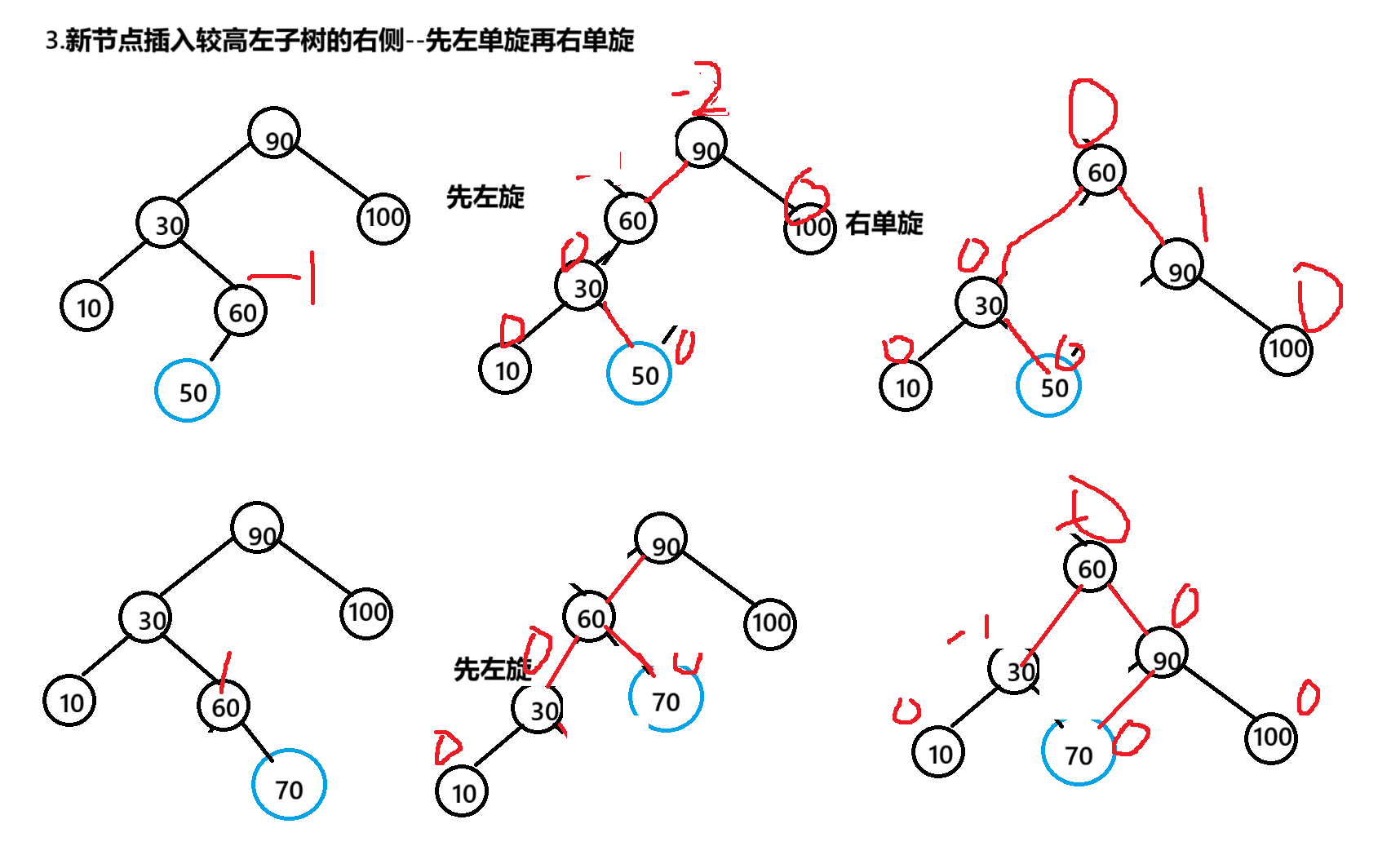

 private static void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if(bf == -1) {subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if(bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}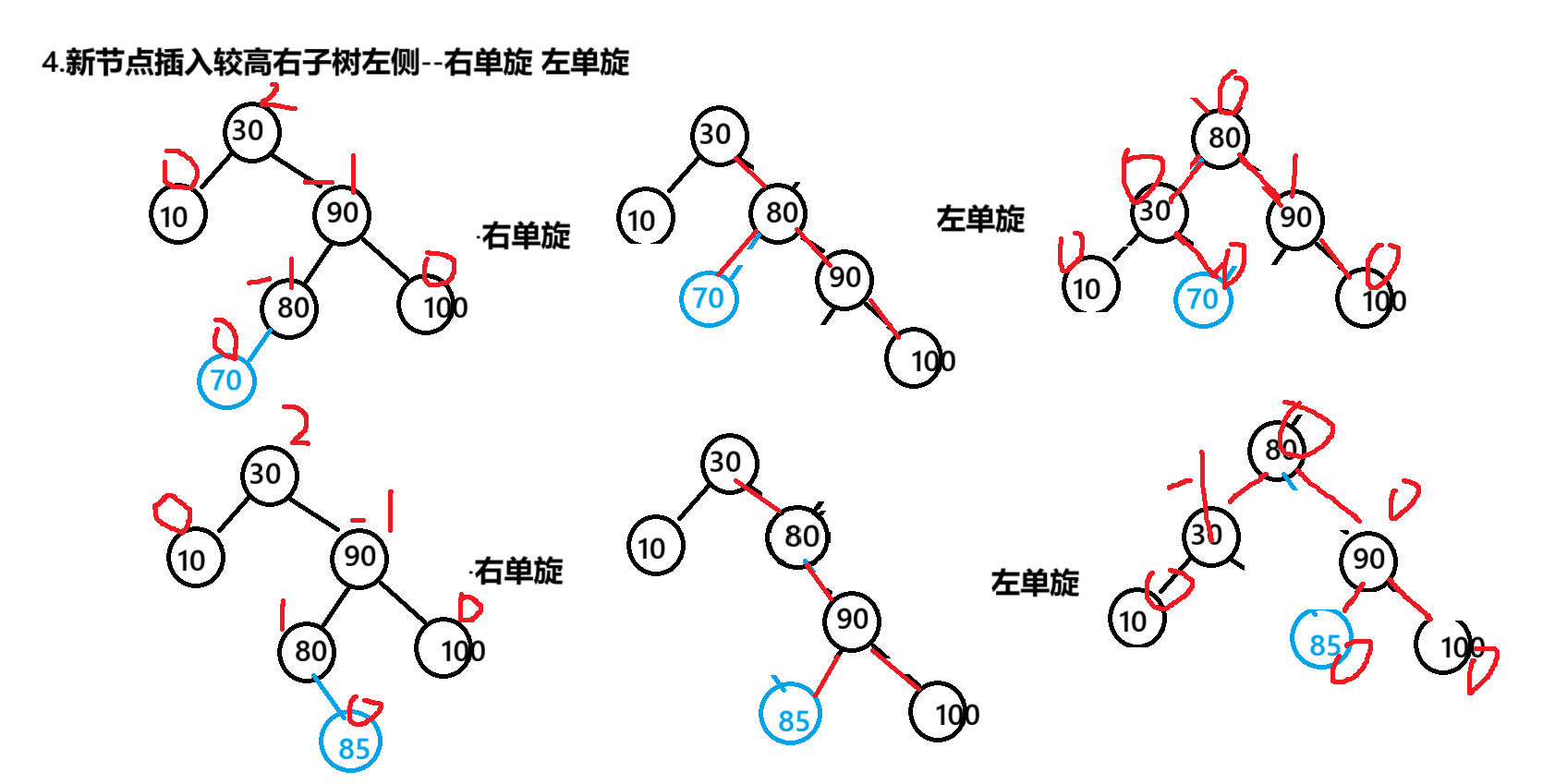

 private static void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == 1) {parent.bf = -1;subR.bf = 0;subRL.bf = 0;}else if(bf == -1){parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}

驗證當前樹是否為AVL樹

高度平衡的二叉搜索樹（不能遍歷AVL樹，因為bf是我們手動設置的，可能會出錯）

  private int height(TreeNode root) {if(root == null) return 0;int leftH = height(root.left);int rightH = height(root.right);return leftH > rightH ? leftH+1 : rightH+1;}public boolean isBalanced(TreeNode root) {if(root == null) return true;int leftH = height(root.left);int rightH = height(root.right);if(rightH-leftH != root.bf) {System.out.println("這個節點："+root.val+" 平衡因子異常");return false;}return Math.abs(leftH-rightH) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}

AVL樹的刪除思路

1.找到要刪除節點

2.按二叉搜索樹刪除規則刪除節點

3.更新平衡因子

性能分析

AVL樹的平衡是通過大量旋轉換來的，適合查找高效且有序的數據結構，而且數據個數為靜態的