貝葉斯的核心思想就是,誰的概率高就歸為哪一類。
貝葉斯推論
P(A):先驗概率。即在B事件發生之前,我們對A事件概率的一個判斷。
P(A|B):后驗概率。即在B事件發生之后,我們對A事件概率的重新評估。
P(B|A)/P(B):可能性函數。這是一個調整因子,使得預估概率更接近真實概率。
1、樸素貝葉斯實現鳶尾花分類
from sklearn.naive_bayes import MultionmialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_irisx,y = load_iris(return_X_y=True)x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=42)
model = MultionmialNB()
model.fit(x_train,y_train)#訓練模型(統計先驗概率)
score = model.score(x_test,y_test)
print(score)#0.6666666666666666x_new=[[5,5,4,2],[1,1,4,3]]
y_predict = model.predict(x_new)
print(y_predict)#[1 2]2、樸素貝葉斯實現葡萄酒數據集分類
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
x,y = load_wine(return_X_y=True)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=42)
model = MultinomialNB()
model.fit(x_train,y_train)
print(model.score(x_test,y_test))#0.9111111111111111x_new = [[1,1,2,1,1,2,1,1,1,1,2,1,1]]
print(model.predict(x_new))#[1]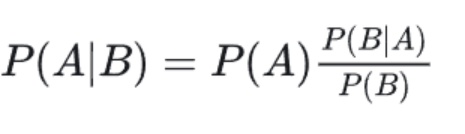



、主機虛擬機(Windows、Ubuntu)、手機(筆記本熱點),三者進行相互ping通)















)