數據結構（9）排序

一、常見排序算法

排序在生活中無處不在，上學這么多年班級排名啥的總有吧，不可能一次都沒見過；打游戲有的排行榜不也是有排序的思想在里面，排序倒不是什么特殊的數據結構，但是是非常重要的算法思想，所以在初階數據結構的最后，學習一下常見的幾種排序算法。

當然，有些算法已經實現過了，比如冒泡排序和堆排序，到時候可以重寫復習一下，但是不再展開具體細節了。

二、插入排序

1.直接插入排序

直接插入排序的思想最經典的對比就是打斗地主，抓牌以后習慣性的就是相同的牌放在一起，一般玩的多的老手也會順手按照升序或者降序排列（當然，按照牌規大小放不一定跟數值升降序一樣）。這就是最常見的插入排序。

當然，實際到對數組的排序肯定是有細節上的差異的，之前我們也大大小小寫過排序的代碼，排序函數的參數也就只數組arr和數組內元素個數，肯定不可能真的存在一個一個插的情況的，但是我們可以自己想想出來一個一個插。

怎么想象出來呢，比如給一個數組：

想想數組為空，現有數組的數據都是要一個一個插入進去的，所以剛開始是：

當然，只看第一個肯定看不出來什么門道，接下來繼續往里插入：

有數據的話再插入肯定就得比較了，將{}類比成手，那里面就是牌，牌肯定按大小排列好看一點。

繼續：

一比較，直接放

比較后前移：

前面幾個例子只能體會到一個一個往后遍歷的循環，但是想象中插入比較交換的循環卻沒能體會到，這個例子就得好好看了。

可見插入（想象出來的）比較，交換實際上也是一個循環。

所以代碼思路基本就有了，外層循環依次遍歷數組中的元素，內層循環使這次遍歷到的元素與前面的元素進行比較，如果不符合想要的順序，那就產生交換，而且比較和交換不止一次，有兩種情況會停止比較和交換，一個是已經符合順序了（比如上面的9，6），另一個是把已經排序（想象中一個一個插入）的數據比較完了，那就該停手將元素放到數組首元素的位置了。

思路一有具體細節代碼見：

外層循環遍歷數組都寫臭了，倒是沒什么好說的。

但是內層循環每次都得有已經排序過的數據的下標，初始值倒是好算，比如這個例子：

最開始插入2,2是待排的（或者說待插的）數據，下標就是i，那i的前一個元素下標也好算，直接i-1即可，但是這個例子很明顯不是比較了一次，而是比較了多次，那么每次下標都得計算：

這樣的話就不得不創建一個變量專門存儲這次比較的兩個數的下標了，這個就有點像冒泡排序內層循環了：

不妨以end為已排序數組的最后一個元素，可知每次進入循環end = i - 1。

那么這次比較的就是end和end + 1（為什么不用i，進循環走幾次就理解了）。

如果想要實現交換肯定得先臨時存下來2，也就是進入循環不僅要計算下標end，也需要記錄下這次插入進的元素。

不過2也別著急放，9一比較往后放是就算了，2可不一定比較一次就放了，很明顯：

一比較2又該前移，或者說6該后移：

循環比較，直到：

比的不能再比了，再比較越界了，那就直接跳出循環，所以進入循環的條件是end>=0。

當然，最后別忘了跳出循環時候把存起來的值放到end+1的位置。

直接寫代碼：

內層循環就是以end作為循環的條件，如果需要換那就把end位置的后移，如果不需要換就結束循環，最后在arr[end + 1]處放置這次插入的數據，思路里面說的非常清楚了。

測試代碼：

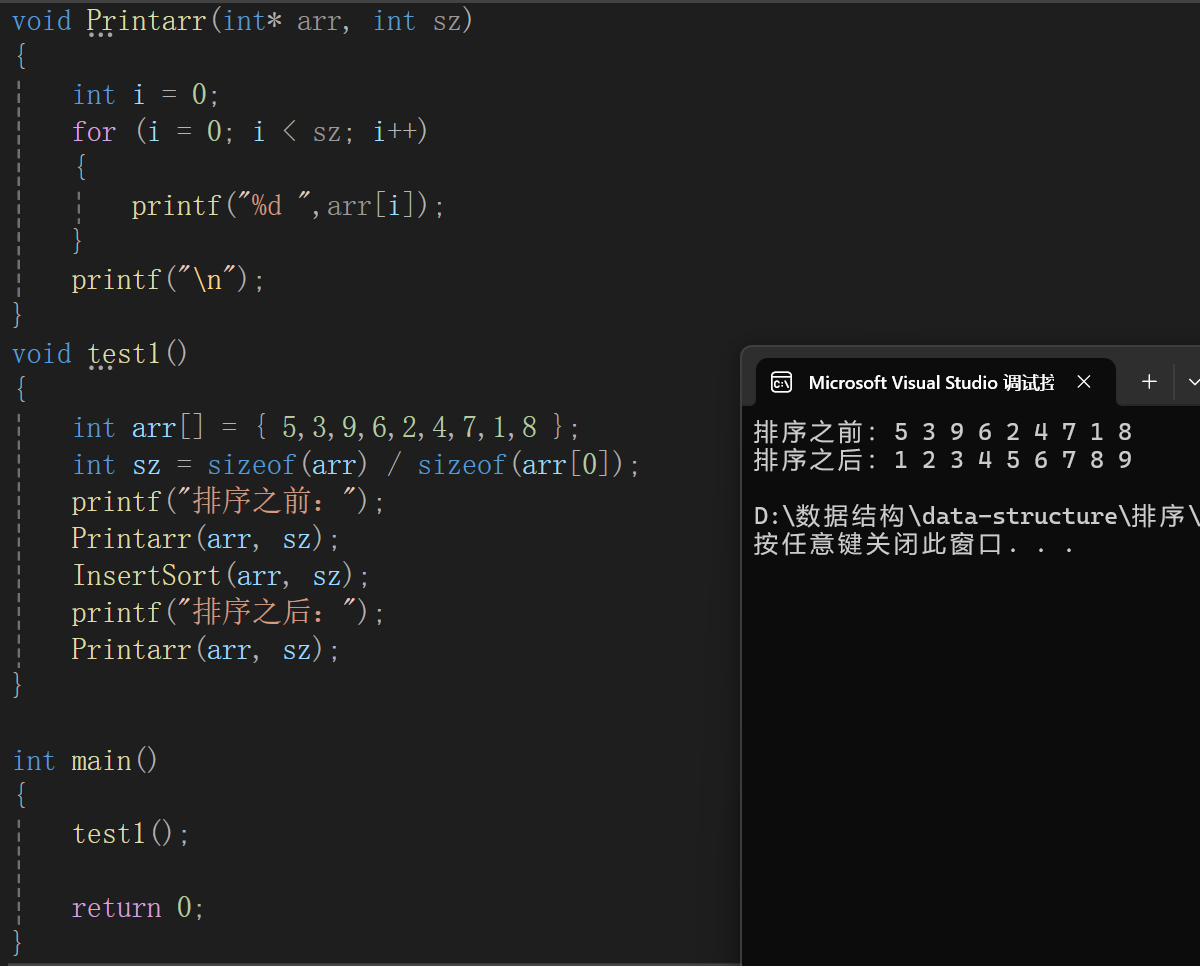
為了方便查看就寫了個Print函數，不多說。

經測試直接插入排序無誤。

時間復雜度

如果按照最壞的肯定是如果想排升序，給的降序數組，這樣的話如果數組大小為n，那么前移的次數就為1 + 2 + ...+ n - 1所以最壞情況下直接插入排序的時間復雜度就是O（n^2）（但是注意，這種情況實在是太少太少，所以一般直接插入排序倒不至于是O（n^2），一般比這個小）。

2.希爾排序

直接插入排序如果遇到與目標順序完全相反的數組序列的話，或者說假如你要排升序序列，結果給的數據是這樣的：

大的在前小的在后，那么這樣也基本n^2的時間復雜度。

為了解決這樣的問題，人們在直接插入排序的基礎上就創造出了希爾排序。

希爾排序的思想如下：
選定一個整數gap（這個gap是步距的意思，具體到例子里就明白了），依據gap將數組分成gap組，對每個gap組進行直接插入排序，所有gap組直接插入排序完以后進行某種運算（一般為gap = gap / 3 + 1，初始為gap = n / 3 + 1，只是為了縮小步距），當gap縮小為1是則為直接插入排序。

可見希爾排序在直接插入排序的思想上提前進行了多次預排序，避免出現與待排序順序完全相反的序列。

注意，這里的gap變化不是依據gap = gap / 3，只是畫圖輔助理解gap的含義。

gap是5，所以就往后數5個數，第gap個正好就是同一組的。

gap理解了以后就得一點一點想代碼怎么寫了：

以這個為例，先考慮一次排序怎么做。

錯誤想法

既然每次排序的每組都是以直接插入排序實現的，直接考慮考慮怎么套直接插入排序看看：

剛上去i = 0肯定也不用移，但是可以知道，如果要進行下一次直接插入排序，不能再i++，如果直接i++就成另外的組了，所以循環變量的變化應為i += gap，同樣由此end每次不能再--而是end -= gap，比較的內層循環也免不了改end初始化為i - gap，后移代碼改為arr[end + gap] = arr[end]。

兩層循環的條件再檢查檢查：

for循環只要不超出數組范圍即可：

while循環

這么一看還是不越界就行。

但是這才是一組的排序：

如果好幾組的話還得再嵌套循環，容易發現gap是幾有幾組，所以用for循環更好：

gap也得變啊，還得套循環計算gap去：

咱就不說時間復雜度到底多少了，就這么多層循環，也少不到哪去，肯定比直接插入排序大，而且說實話，兩層循環的時候調試或者改代碼都難讀的很，這都4層了，那還不得炸了。

正確做法

所以上面的思路肯定行不通，畢竟希爾排序可是直接插入排序的優化，索性這么干：
不套直接插入排序的代碼，依次遍歷實現直接插入排序，什么意思呢？

外層for循環還是遍歷整個數組，內層循環實現組內比較和互換即可，畫圖理解：

這樣分組i = 0和i = 1沒啥好看的都是組里第一個元素，也不比也不移，直接從i = 2開始。

明顯end初始化就為i - gap，需要存的temp還是i所指元素，進入while循環顯然的比較對象應該是end和end - gap，且end不能越界，end如果是下標為0，再讓arr[end]和temp比較，故循環條件為end >= 0，內層比較條件和循環變量注意即可。

最外層gap注意循環條件即可，最內層弄清楚下標。

時間復雜度

由于希爾排序時間復雜度實在太復雜（可不要以為三層循環就是n^3），可以說到了算無可算的地步了，只需要知道肯定比直接插入排序的n^2低即可。

三、選擇排序

1.直接選擇排序

直接選擇排序就是一次次的遍歷數組，把這次遍歷到的數組最大和數組最小放在數組的頭和尾，直至遍歷完整個數組。

還是以這個數組為例：

遍歷數組肯定免不了用下標，而下標起名也好起：

從兩邊往中間遍歷，這樣的話，最后找到min和max就能直接給begin和end位置的數據賦值。

細節直接看代碼：

一次選擇排序選最大選最小，比較需要注意的是for循環的起始條件和循環的限制。

因為min和max初始為begin所以遍歷的時候不需要自己跟自己比較了，并且越界條件是超出未排序元素的下標（已排序的已經保證比現在待排的最大或者最小了）。

只不過在遍歷的時候出了一點意外：

如果按照我們寫出來的代碼來看，arr[begin]和arr[min]互換一次，arr[max]和arr[end]互換一次，這樣不就相當于沒有換嘛，所以這種begin是max，end是min的前情況得想辦法克服。

要不然如果碰見就交換一次，但是有點小麻煩，干脆如果max剛好是begin，min剛好是end，就還是先交換，但是max換為了得讓max跟上：

最后外層while循環條件基本上就得往begin和end的關系靠一靠了：

可以很明顯看出來，相等就不用再排了，同樣的，如果begin比end還大，那也不用排了，所以循環條件是：

最后代碼：

測試代碼：

時間復雜度

基本上看來是這樣的，因為我們這個也算是改進過的直接選擇排序（一般直接選擇排序每次找最小的放到前面就行了），進入循環的次數是n - 1 + n - 3 + n - 5 +……+0（當然，最后不一定是0），再估算基本就是O（n ^ 2）。

2.堆排序

堆排序代碼直接手打了：

測試代碼：

時間復雜度

沒啥好說的nlogn。

四、交換排序

1.冒泡排序

接觸過的第一個排序算法，那時候還在學C，現在數據結構初階都快干完了。

不多bb：

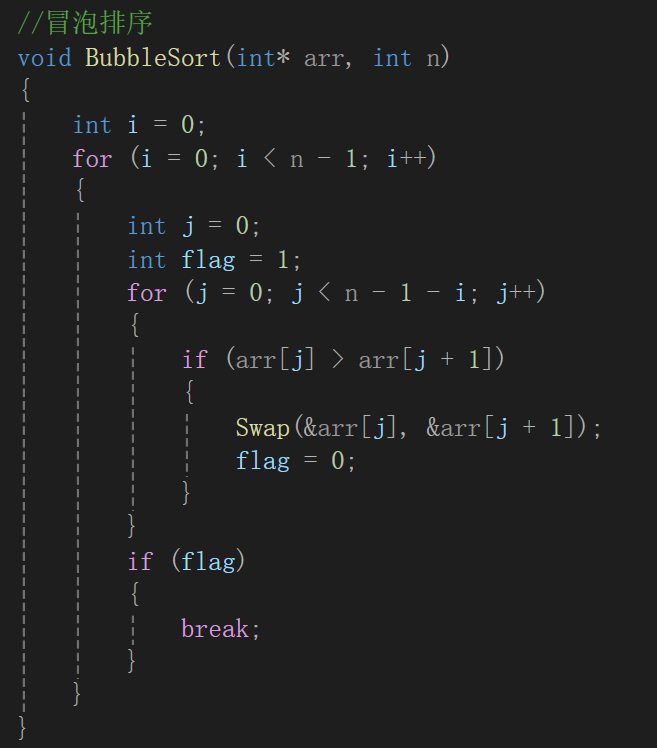
測試代碼：

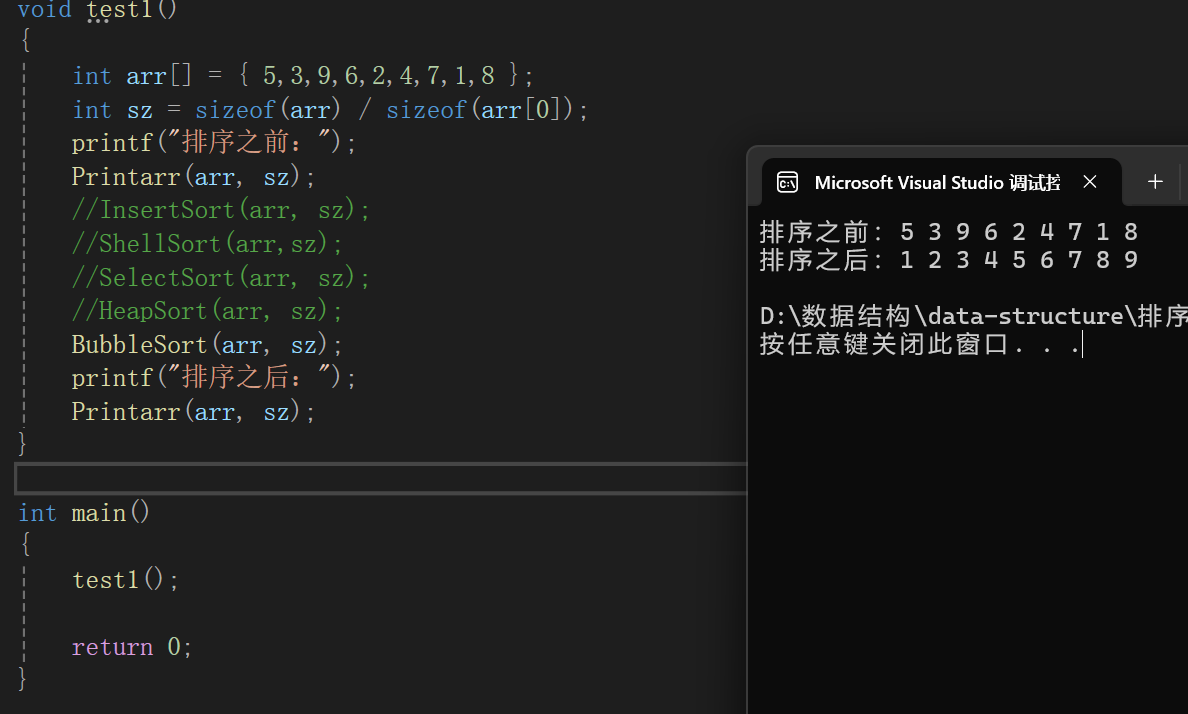
時間復雜度

n^2，經典的循環套循環。

2.快速排序

快速排序人如其名，可以說沒有什么突出的特點，就是一個快字，借助的思想就是二叉樹的思想，可不是跟堆排序一樣，時時刻刻都在保證數組就是個堆，只不過如果畫圖的話，看起來像一棵二叉樹。

核心思路就是選取一個基準值，依照基準值的大小，將數組序列分成左右兩個子序列，左子序列是比基準值小的值（不一定有序），右子序列是比基準值大的值（不一定有序）。重復此過程，最終，所有元素都會排列到相應位置。

基準值倒是可以隨便選，但是基準值可不是生來就是左序列比它小，右序列比它大，我們得想辦法實現出來。

當然，這個操作的實現可不止一種，所以接下來慢慢講：

①hoare版本

比如這樣一個序列：

咱也不亂弄，就讓數組第一個元素當基準值，接下來就借用兩個指針和一個哨兵：
?

key站在這次的基準值

left指針從左往右遍歷，找比基準值要大的數

right指針從右往左遍歷，找比基準值要小的數

為什么left和right要這么做呢？

其實是如果在key左邊有比key大的數，肯定得放到key后面；如果在key右邊有比key小的數，肯定要放在key前面。但是在確定key位置前，很明顯的我們不知道該把left往哪放才算往后放，right往哪放才算往前放，所以這時候就要swap：left和right。

我們可以遍歷試試：

每次判斷left和right的指向值，不符合我們找的值就left++right--。

交換過以后也要++--。

相等也要繼續遍歷：

但是這么一找，明顯越界了，所以一旦越界了，就該插入key了，因為我們已經整理好左右子序列了，這就倆指針，一個right，一個left，我也不知道為啥，直接跟right交換就行。

這樣一次找key就結束了，結果是這樣的：

key指向的元素歸位了，接下來就是循環這兩個子序列了，基本操作是一樣的，key就是子序列最開頭的元素：

確定好區間：

剛才光顧著討論跳出循環以及什么時候互換，忘了說一個玩意，我們left和right指針遍歷的應該是除了key以外的元素，畢竟key所指元素一直要被比，所以left初始弄個key + 1或者說key就是此次數組的第一個元素，left再++。

循環截止的條件也能看出來點門道，如果只有一個元素，或者說沒有元素的話，直接就可以停止循環了，當然，帶上下標更清楚一點：

如果再分，就是[4,4]和[6,5]區間，很明顯，一個是左等右，一個是區間不存在。

最左側的還得再分，但是最后肯定可以得到：

成功實現了排序，從這里也可以看出來類似于二叉樹的左右子樹一樣，所以干脆我們還用遞歸寫代碼：

快速排序的參數講究的有點多，因為我們快速排序的時候要的是區間，有的人一看就說，你傳n以后自己計算區間從哪到哪不完了，但是遞歸呢，遞歸以后還要自己計算嗎，這個left和right很好的代表了區間的左右，而不僅僅是為排序數組的首元素下標和尾元素下標。

放key的實現講究太多，單獨封裝成函數來看：

right和left的移動可不止一次，所以直接給一個while循環，while循環去找right和left目標值是沒錯，但是在這之前還得保證不能越界：

這里就是很好的例子，一越界就停手吧，雖然成功找到了比key小的數，這樣再交換豈不成無底洞了，早晚right得到key的位置，這其實是我們不想看到的。

另外，碰見相等的也不能等，有這樣的例子：

如果寫了等號，那就會瘋狂的向左遍歷right指針，一越界就停止，這樣會導致遞歸的樹穩定為n層。

即：

不寫等號可能對半分分遞歸就結束了，遞歸的次數基本上就是能分出來的二叉樹的層數，但是一旦寫上等號，不說right穩定得遍歷到數組最左端，光說產生的遞歸的樹都得n

即logn變n。

②lomuto版本

lomuto版本的主體思路大概如下：

用兩個指針，一個是pcur，一個是prev，prev指針初始指向pcur指針前一個。pcur的作用是用來遍歷整個數組，找比key要小的值。

具體細節如下：

pcur指針往后遍歷，尋找比key指向的值要小的值。

1)如果找到了，prev++，并將此時prev和pcur指向的元素互換，互換完以后prev繼續站崗，pcur++

2)如果找不到，pcur++

比如這樣的例子：
符合交換條件，prev++，再swap掉prev和pcur

但是遇到prev == pcur就沒有必要再互換，直接pcur++就行。

循環遍歷：

又是相等不用變，pcur++

這次遍歷到的很明顯就比key要大了，那就不管它繼續往后遍歷，直到碰見比key小的。但是在此之前，觀察到prev++后指向的要比key要大，所以這種遍歷prev后面的要不然就直接是pcur指向的，不用互換，要不然就是比key要大的，一跟pcur互換不就是實現了小在key前，大在key后之類的操作嗎。

展示其中一次不相等的互換：

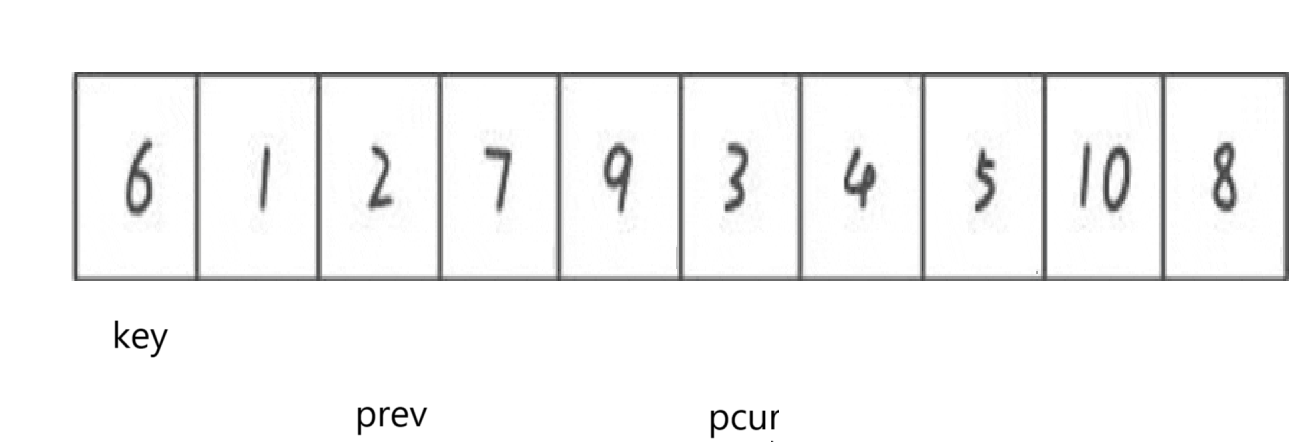
找到了就prev++

swap

swap結束pcur++

也不廢話了，直接展示遍歷完以后：

這時如果swap key和prev所指向：

剛好實現基準值前比它小，基準值后比它大。

代碼實現：

當然，內層if嵌套可以合并一下：

遞歸的代碼不變：

測試代碼：

遞推版本快速排序的時間復雜度和空間復雜度的分析

時間復雜度基本上得類比我們做二叉樹oj題的思路，因為代碼產生了遞歸，可知，時間復雜度 =?? 遞歸次數*每次遞歸的函數的循環次數。

但是對于我們這段代碼時間復雜度卻不能死板的套公式去算：

如果按照公式順著走下去的話，倒是可以硬解，假設結點剛好能夠湊夠滿二叉樹，每層還都能對半分序列，這樣的話有：

每層都是結點個數 *? 每個子序列時間復雜度（因為相當于遍歷整個數組，所以基本等于結點個數）

1 *? n + 2 * n / 2 + 4 * n / 4 + ……+? $2^{log(n + 1) - 1}$ ? * 1

而 $2^{log(n + 1) - 1}$ ? * 1基本也是O(n)

有多少層呢logn層

所以時間復雜度為O(nlogn)。

當然，可以用分割的思想，如果一層一層來看的話，其實每層子序列合起來剛好就是原數組的長度，這樣想的話很容易想到每層時間復雜度都是O(n)，并且有logn層，很容易得到時間復雜度就是O(nlogn)。

空間復雜度一般是不必多說的，但是對于這種類似于在棧區構建出來函數二叉樹的代碼還是來見見世面。這種遞歸代碼時間復雜度的產生就是因為函數棧幀的創建：

如果沒有回歸的話，就會從一個函數棧幀跳躍到另一個函數棧幀里去，這樣的話很容易想到，總有一條路是最長的，比如其它最多分兩三層，它能分5層，這樣得創建5次函數棧幀，其實這個最大值應該就是樹的高度，我們估算的話就是logn層嘛，所以空間復雜度就是O（logn）。

③非遞歸版本——借助數據結構棧

棧里面存的是本次需要找基準值的區間，通過入棧出棧實現對不同區間的基準值的查找以及遞歸區間的分割。

找基準值我們實現了兩種方法，所以找基準值到時候直接寫就行，問題是我們如果通過棧實現類似于函數遞歸的效果呢？
比如現在第一次找到基準值以后，就應該分開左右子序列，按照上面所說，我們分別需要在棧里存0,4和6,9并分別在子序列中尋找新的基準值，后面的不再口頭描述，直接看到最后：

帶上棧：

左邊界大于右邊界的就寫了一個，只要key在邊緣就會產生，可知，如果子區間左值等于右值，或者子區間左值大于右值，都是無需再排列的子序列，不再入棧。

代碼表達：

測試代碼：

五、歸并排序

1.歸并排序基本思路

歸并排序基本思路就是把不斷的把得到的數組二分拆開，得到有序的子序列后再不斷合并得到最終的有序序列。

比如上圖，最開始輸入的序列基本都是無序的吧，不斷的二分，使得數組最終被分割為一個又一個的元素，如果只看每個元素的話，每個元素自己都是有序的，接下來合并，思路就是合并兩個有序數組，這個思路在OJ題里見識過，大致思路還是一樣的。最終得到的數組就是有序的。

而分割數組類似于快排每次找完基準值后的分割，所以可以嘗試用遞歸實現，即大體步驟為：
遞歸分割和合并兩個有序數組

2.代碼實現

遞歸分割

很明顯如果想要分割，看成區間的話，區間左端和右端都得十分清楚，才能算出來區間中點，所以遞歸的函數我們就傳左端點和右端點的值。

看著圖其實很容易寫出來代碼，實際上這個分割類似于快排，不是真的分割，只不過給的區間導致能訪問到的元素類似于分割的效果。

遞歸有遞推肯定還得有回歸，回歸條件很明顯，如果這次區間左等右，也就是只有一個元素的時候，就該回歸了。

拆分完全以后就可以兩兩進行合并了：

就看這兩個序列，合并兩個有序數組的代碼肯定免不了循環，因為需要往目標數組里存放的值肯定不止一個，而且如果一個數組遍歷完以后，就應該停下來，防止越界比較，這樣肯定會存在一個數組放完了，另一個數組還沒有訪問，所以得三個循環才能保證最終兩個數組的元素都被有序的放到了目標數組中。

有思路了，寫代碼前我想應該畫一下圖，看看執行思路大概是什么：

我們從單個的元素的序列合并成兩個元素的序列我們采取原地修改會將原數組順序改成：

現在有左序列區間[left,mid]右序列區間[mid + 1,right]，這時候就發現了一個問題：

不管是找兩個序列的最大的放到序列末尾，還是找到最小的放到序列開頭，都可能會導致未排序的數據被覆蓋，如果這樣肯定排序就會失敗。

我們每次放之前存一下的話等于還得用一個變量index去記錄這次該放的位置的下標，以及temp保存下標對應的元素，這樣的話每次取出來的可就不只是有序數組里的兩個元素了，也就是每次放都得考慮兩個有序數組里取出來的和temp里存放的。

這么寫又出現問題了，假如現在插入小的：

你temp存的就應該是6對吧，存6以后遍歷左邊子序列的指針肯定不能再指向6了，得指向temp，但是如果指向temp的話你該怎樣遍歷原子序列6后的10呢，難不成還得再存一下嗎？
所以原地插入實在是太麻煩了，我們OJ題里可以實現原地插入純純是因為當時的題給的有空位：

所以才往空的地方先插大的。

原地實現歸并排序太麻煩為何不嘗試一下創建一個等大的臨時數組呢？

遞歸函數分割的時候確實不需要temp這個臨時數組，但是一旦開始合并就需要了，所以索性遞歸函數加上temp這個參數，而排序結束及時歸還操作系統我們申請的空間，所以歸并排序主函數邏輯就是如此了，那么細節就是看遞歸函數了：

分割其實還是不用變，但是一旦分割到頭，如：

這里就是左右子樹都分割好了，就得合并了，直接就著現有指針實在是太抽象了，所以我們不妨創建幾個變量：

而且注意，我們的思路是拿著有序序列，檢測著先后順序往temp里放，一旦組合完成就返回給arr，所以我們循環內部判斷大小引用的是arr里的值（如果剛分割完還沒放，temp為空也沒辦法訪問，都是隨機值）

但是寫著寫著發現又有問題了，如果以遍歷子序列的指針遍歷temp數組的話，就會很明顯的發現，你begin1小那放begin1，遍歷過了就++，但是如果begin2大的話，begin1現在指向的元素實際上是沒有插入temp里，但是你為了遍歷temp的指針放到正確的位置，還是++了，所以現在就應該單獨給遍歷temp數組創建一個變量：

這樣就合理多了。

我們說過了，這個循環結束一定還有元素未放：

最后把temp里的元素給arr復制過去：

選擇用memcpy，但是不知道得傳多大空間，所以畫圖看一下：

很明顯(right - left + 1) * sz(int)個字節。

但是還有細節，如果遍歷到這里：

arr是數組首元素的地址，這兩個數組合并的話應該是從temp + left開始逐個從arr + left開始復制，不然只會去修改從首元素開始的right - left + 1個數據。

所以最終代碼：

測試代碼：

時間復雜度和空間復雜度分析

時間復雜度還是和快速排序類似，畢竟都是分樹，樹每層總得時間復雜度就是O（n），容易得到樹的層數就是logn，所以時間復雜度就是O（nlogn）。

空間復雜度直接看總的代碼：

一個是temp，一個是遞歸函數的函數棧幀的創建，很明顯O（n + logn），那么空間復雜度就是O（n）。

六、測試所有比較排序的性能

有這樣一段代碼：

創造十萬個數據來查看具體時間的快慢，與時間復雜度對照：

直接插入排序最壞是O（n^2），但是最壞情況是小的數據都在后面，大的數據都在前面，實際情況下其實不一定達到，所以直接插入排序時間復雜度實際達不到的多。

希爾排序很少討論它的時間復雜度，因為希爾排序時間復雜度不好計算，一般認為O（nlogn~n^2）

直接選擇排序我們實現的時候是用兩個指針，一個找最小，一個找最大，其實每次都遍歷完了、最后不管數據什么情況都是O(n^2)，但是由于數據量太小，所以顯得我們直接插入排序時間復雜度其實小于冒泡排序，但是多次試驗以后基本都是冒泡的一半。

堆排序不必多說，O(nlogn）深入人心。

快排歸并都剛寫，O（nlogn）

冒泡排序典型循環套循環，O（n^2）毋庸置疑。

七、計數排序

1.原理即實現

實際上我們常見的排序是八大排序，但是我們見得比較排序只有其中啊，插入排序的直接插入排序和希爾排序，選擇排序的直接選擇排序和堆排序，比較排序的冒泡排序和快速排序，以及歸并排序。

既然計數排序不屬于比較排序，難道屬于不比較排序，嗎，但是這其實有點匪夷所思，不比較大小我怎么能知道哪個大哪個小，不妨來看一下計數排序：

計數排序的原理是運用哈希直接定址法對相同的數據進行計數，并最終將計數結果還原到原數組里。

具體操作如下：

從小到大計數：
1：2

2：2

4：3

6：1

9：1

創建一個數組，專門用來存儲計數的結果，其中下標為原數據，數組元素為計數數據：

當然，空白的地方不是沒有數據嘛，就存0，所以到時候要不然calloc，要不然malloc以后memset，反正動態開辟的數組默認值為0。

遍歷我們的計數數組，寫一個循環，外層循環的次數是數組元素大小，內層不斷往原數組里塞下標，直至遍歷完整個計數數組。

即：

老說什么哈希映射，哈希不哈希不管，確實是體會到了映射。

但是寫代碼之前再整一個例子，因為開辟的數組空間大小還有個講究：

如果仍舊按照最大元素的值創建數組，按照下標照應原數值的原理，我們realloc的大小實際上是max + 1，因為數組下標是從0開始的嘛，這樣就會造成其實基本100個空間的浪費，因為0~99根本不會存放元素，當然，下標100往后也不是每個都存，但是至少可以接受那么一點點浪費。

所以一般會做此處理：
寫一個循環遍歷整個數組，找出最大值最小值，根據最大值和最小值的差確定數組大小，比如這里的max = 109，min = 100，假設這中間每個元素都存在的話就是max - min + 1個元素，所以到時候數組的大小就得搞個max - min + 1個元素。

這時候往里存肯定就得先-min，不然下標不好照樣，到時候還原的時候+min就行，比如這個例子

處理后應為：{0,1,9,5,1,5}

如果存起來的話應該是：

0：1

1：2

5：2

9：1

到時候還原的時候下標+min就行。

思路清楚代碼表達：

說啥做啥，所以代碼不再解釋。

可以看到其實還是比較了，至少遍歷整個數組給出了最大值和最小值，只不過正兒八經改變數組的時候確實不需要比較。

測試代碼：

2.限制

分析計數排序的時間復雜度可以得到：
O(n + range)

復雜度其實不老好分析，畢竟range取決于所給序列的最大值和最小值的差值。

所以為使時間復雜度趨近于O（n），一般只適用于數據大小比較密集的序列。

八、所有排序算法時間復雜度及穩定性分析

排序?法	平均情況	最好情況	最壞情況	空間復雜度	穩定性
直接插入排序	O( $n^{2}$ )?	O(n)?	O( $n^{2}$ )?	O(1)	穩定
希爾排序	O(nlogn) ~O( $n^{2}$ )?	O( $n^{1.3}$ )	O( $n^{2}$ )?	O(1)	不穩定
直接選擇排序	O( $n^{2}$ )?	O( $n^{2}$ )?	O( $n^{2}$ )?	O(1)	不穩定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不穩定
冒泡排序	O( $n^{2}$ )?	O(n)	O( $n^{2}$ )?	O(1)	穩定
快速排序	O(nlogn)	O(nlogn)	O( $n^{2}$ ）	O(logn)	不穩定
歸并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	穩定