一、決策樹

1. 決策樹有一個很強的假設：

????信息是可分的，否則無法進行特征分支

2. 決策樹的種類：

2. ID3決策樹：

ID3決策樹的數劃分標準是信息增益：

信息增益衡量的是通過某個特征進行數據劃分前后熵的變化量。但是，它沒有考慮到特征本身的熵，因此容易偏向于取值較多的特征。

3. C4.5決策樹：

C4.5決策樹的數劃分標準是信息增益比：

信息增益比則是 信息增益 除以 該特征自身的熵（也稱為分裂信息）。這種方法旨在糾正信息增益對于取值較多特征的偏愛，通過將信息增益與特征自身的熵相除來懲罰那些擁有大量取值的特征。

C4.5并沒有直接偏向于取值少的特征，而是通過分裂信息來調整信息增益，使得特征的基數大小影響其最終的選擇概率。這種方式幫助算法避免了僅僅基于信息增益選擇特征可能導致的過擬合問題，特別是當存在高基數特征時。

4. CART 回歸樹 和 分類樹：

回歸樹：每個子樹的輸出是該子樹節點值的均值：

步驟(1)：選擇最優切分變量和切分點

步驟(2)：劃分區域并決定輸出值?

根據特征jj和切分點ss將數據集劃分為兩個子區域

計算子區域內的樣本目標值的平均值作為該區域的預測值

這兩個步驟描述了遞歸地應用上述過程，直到滿足停止條件，并最終生成決策樹的過程。

5. CART 的參數：?

6. CART 訓練后的回歸樹常用屬性：

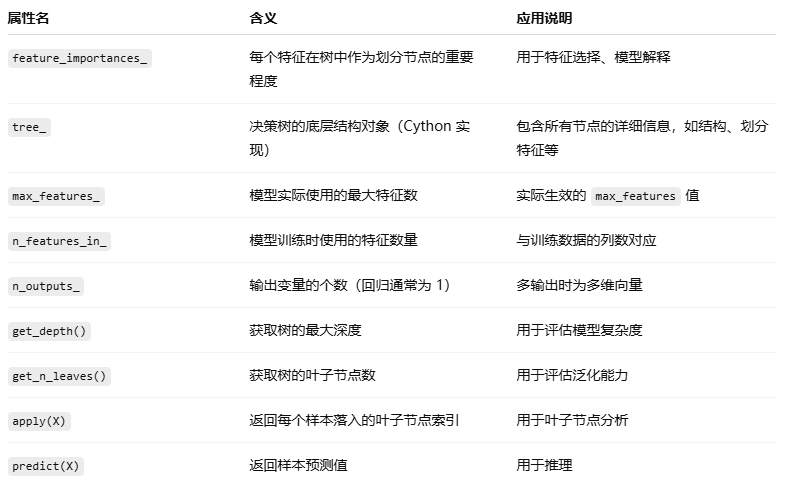
為什么獲取樹的葉子節點數 就可以用于評估泛化能力？

???????葉子節點數量越多，意味著決策樹越復雜。每個葉子節點代表一個具體的預測規則或輸出值。如果一棵樹的葉子節點過多，說明它可能已經學習了訓練數據中的很多細節甚至是噪音，這種現象通常被稱為過擬合。過擬合模型在訓練集上表現很好，但在未見過的數據（測試集）上的表現較差。

7. 回歸樹demo展示，可視化回歸樹：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt# 1. 加載數據
data = load_iris()
X = data.data
y = X[:, 0]  # 用 sepal length 做回歸目標# 2. 數據劃分
X_train, X_test, y_train, y_test = train_test_split(X[:, 1:], y, test_size=0.2, random_state=42)# 3. 建立模型
reg = DecisionTreeRegressor(max_depth=3, random_state=42)
reg.fit(X_train, y_train)# 4. 模型預測與評估
y_pred = reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"\n【模型評估】\n均方誤差 MSE: {mse:.4f}")# 5. 打印常用屬性
print("\n【模型屬性展示】")
print("特征重要性 feature_importances_:", reg.feature_importances_)
print("使用特征數 n_features_in_:", reg.n_features_in_)
print("輸出維度數 n_outputs_:", reg.n_outputs_)
print("實際使用的 max_features_:", reg.max_features_)
print("樹最大深度 get_depth():", reg.get_depth())
print("葉子節點數 get_n_leaves():", reg.get_n_leaves())# 6. 可視化特征重要性
feature_names = data.feature_names[1:]
plt.figure(figsize=(6, 4))
plt.bar(feature_names, reg.feature_importances_, color='teal')
plt.title("Feature Importances")
plt.ylabel("Importance")
plt.grid(axis='y')
plt.tight_layout()
plt.show()# 7. 可視化樹結構
plt.figure(figsize=(10, 6))
plot_tree(reg, feature_names=feature_names, filled=True, rounded=True)
plt.title("Decision Tree Structure")
plt.show()

8. 分類樹：

sklearn 的模型參數：

模型屬性對比：

demo：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 1. 數據準備
iris = load_iris()
X = iris.data
y = iris.target# 2. 劃分數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 3. 構建模型（使用信息增益）
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)
clf.fit(X_train, y_train)# 4. 預測與評估
y_pred = clf.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"準確率: {acc:.4f}")# 5. 展示分類專有屬性
print("\n【分類樹專有屬性】")
print("類別標簽 classes_:", clf.classes_)
print("類別數量 n_classes_:", clf.n_classes_)
print("每個測試樣本的預測概率 predict_proba():\n", clf.predict_proba(X_test[:5]))

?二、Boosting：

Boosting?中文是“提升方法”，是一種集成學習方法，它只是一個“策略思想”。

AdaBoost、GDBT、 XGBoost、LightGBM 都是這個思想的具體實現。

Boosting 將多個弱學習器（weak learner），如小決策樹，串行地組合在一起，每一輪都“糾正”上一輪的錯誤，最終得到一個強大的集成模型。

Gradient Boosting：英文縮寫 GDBT ，中文是“梯度提升樹”或“提升樹”、“提升樹模型”。

（2）Gradient Boosting：英文縮寫 GDBT ，中文是“梯度提升樹”或“提升樹”、“提升樹模型”。

注意：提升樹 ≈ GBDT（及其變種） ≠??AdaBoost?

1. AdaBoost：

注意：不同于GDBT，AdaBoost 在第 t 輪不直接使用前一輪訓練出的模型，而是通過樣本權重的改變，間接地反映之前模型的表現。

AdaBoost 每一輪都是從頭訓練一個新的弱學習器???，只是通過每次迭代將?訓練樣本分布進行調整，令錯分樣本權重更大

2. GDBT：

GBDT 是一種通過迭代擬合損失函數負梯度（即殘差）的方式訓練多個決策樹并進行加權求和的Boosting 方法。GDBT使用回歸樹作為弱學習器（哪怕是分類任務）。

GBDT 的“Gradient”不是裝飾，它真的是在做梯度下降，只是回歸時，常用的損失函數是平方誤差（MSE）的公式為：

?

對于MSE 的負梯度為：

MSE的負梯度剛好有一個可描述的名字，就是殘差，因此可以理解為一種巧合hh

再舉個例子：

GBDT 用于二分類，使用對數損失（Log Loss）：

那么，在 GBDT 的每一輪中，就是用這些 負梯度 gi? 作為新的“偽標簽”來訓練一個 回歸樹。在新的一輪迭代中，這個回歸樹試圖學習xi → gi 。該回歸樹不是去做分類，而是用回歸樹去逼近這個負梯度值（偽殘差）

你看到的是“殘差”，其實它背后是“負梯度”；
這個巧合讓 GBDT 在回歸問題上看起來像“殘差堆樹”，但本質上是一種通用的函數空間梯度優化方法。

1. 集成學習：

2. Boosting 工作機制：

Boosting 的每一輪訓練模型都試圖學習 當前預測值與真實值之間的差值（殘差），從而逐步縮小誤差。?

Boosting 不是一開始就擬合目標，而是每次都只擬合 還沒學會的部分，就像學生每天復習昨天不會的題，反復訓練，直到掌握。

?

提升樹算法通過逐次擬合殘差并不斷優化模型，能夠有效地提高模型的預測精度，且避免模型過擬合，具體來說，原因如下：

（1）逐步擬合殘差，避免直接過擬合目標
每一步學習的目標是上一步的誤差（殘差），不是一次性“猜中全部”。
這種“加法模型”方式可以讓模型以小步慢走的方式逐漸逼近真實目標。

（2）模型弱但組合強
Boosting 通常使用弱學習器（如深度很淺的決策樹）。
單個模型能力弱，不容易過擬合，但組合起來又能表現強。

總結參考：

感謝大佬的無私分享，同時加入了一些自己的總結和理解，歡迎批評指正，相互交流~

決策樹（ID3、C4.5、CART）的原理、Python實現、Sklearn可視化和應用 - 知乎