1.P與NP問題

我們之前就對P與NP問題有所了解。
有些計算問題看起來很難解決。盡管我們進行了多次嘗試，但我們仍然不知道這些是否存在高效的算法。然而，我們也無法證明這些問題確實很難解決。我們只是“不知道”或者不確定，至少在目前是這樣。用更正式的語言來說，我們不知道P是否等于NP，或者P是否不等于NP。

1.1 計算上難以解決的問題（Hard Computational Problems）

例如前面我們提到的 { 0 , 1 } \{0,1\} {0,1}背包問題。
輸入：一組物品 { i 1 , i 2 , . . . , i n } \{i_1,i_2,...,i_n\} {i1?,i2?,...,in?}，其中每個物品$i_j$有一個整數重量$w_j>0$和一個整數收益$b_j$。同時，給定一個最大重量$W$。
目標：找到一個物品的子集，使得這個子集的總重量不超過$W$，并且總收益最大化。注意，不允許取物品的分數部分。

這里我們室友動態規劃解決該問題，起時間復雜度是$O(nW)$，其中$n$是物體的數量，$W$是背包的最大承重。這個時間復雜度不是多項式時間復雜度，在$W$非常大時仍然會非常慢。動態規劃解決方案確實與W的值成線性關系，但與$W$的長度（即W的二進制表示的位數）成指數關系。
例如，如果$W$是$1000000$，那么W的二進制表示大約是$20$位（因為$2^{20}\approx 1000000$）。因此，算法的運行時間是$O(n\times 2^{20})$，這與W的長度成指數關系。

1.2 決策問題和優化問題（Decision/Optimization problems）

決策問題（Decision problems）指對于一個計算問題，其輸出“是”或“否”。換句話說，決策問題的答案是一個布爾值（True或False），表示某個條件是否滿足。
優化問題（Optimization problems）中我們的目標是最大化或最小化某個值。
優化問題可以通過添加一個參數$k$來轉化為決策問題。具體來說，我們可以通過以下方式將優化問題轉化為決策問題：
如果優化問題是最大化某個函數$f(x)$，那么可以轉化為決策問題：是否存在一個解$x$，使得$f(x)\ge k$？
如果優化問題是最小化某個函數$f(x)$，那么可以轉化為決策問題：是否存在一個解$x$，使得$f(x)\le k$？
如果一個決策問題是難解的（即沒有已知的多項式時間算法），那么其相關的優化問題也必定是難解的。

例如我們前面的 { 0 , 1 } \{0,1\} {0,1}背包問題就是一個優化問題，我們的目標是最大化收益函數。因此我們也可以得到其的決策問題版本。
輸入：一組物品 { i 1 , i 2 , . . . , i n } \{i_1,i_2,...,i_n\} {i1?,i2?,...,in?}，其中每個物品$i_j$有一個整數重量$w_j>0$和一個整數收益$b_j$。同時，給定一個最大重量$W$和一個整數$k$。
問題：是否存在一個物品的子集，使得這個子集的總重量不超過$W$，并且總收益至少為$k$？
如果我們可以高效地回答決策問題，那我們就可以高效地解決相關的優化問題。
因此我們通過決策問題的高效解決，我們可以使用二分搜索來找到優化問題的最優解。
具體步驟如下：

1. 設定收益的范圍，從最小可能收益到最大可能收益。
2. 使用二分搜索，在這個范圍內查找最大收益，使得決策問題的答案為“是”。
3. 每次二分搜索的中間值作為$k$，詢問決策問題。
4. 如果決策問題的答案為“是”，則最優解可能在更高的收益范圍內；如果答案為“否”，則最優解可能在更低的收益范圍內。
5. 重復這個過程，直到找到最大收益，使得決策問題的答案為“是”。

1.3 計算問題的正式定義

這一部分的知識與上學期知識類似。

計算問題的輸入被編碼為有限的二進制字符串$s$。字符串的長度表示為$\mid s\mid$。
我們將決策問題與一組字符串聯系起來，對于這些字符串，答案是“是”。
我們說算法$A$接受輸入字符串$s$，如果$A$在輸入$s$上輸出“是”。

這個概念可以用上學期的圖靈機去理解。現在我們有一個圖靈機對算法$A$是否接受輸入字符串$s$進行判斷。它會對接受的字符串$s$輸出“是”。最后決策問題就是包含所有結果為“是”的輸入字符串$s$的集合。

對于某個決策問題$X$，用$L(X)$表示應該被該問題的算法接受的（二進制）字符串的集合。
我們通常將$L(X)$稱為一個語言。
這與上學期的知識一致。
我們說算法$A$接受語言$L(X)$，如果對于每個字符串$s\in L(X)$，算法$A$輸出“是”；而對于不在$L(X)$中的字符串，算法$A$輸出“否”。

下面我們給出 { 0 , 1 } \{0,1\} {0,1}背包問題的決策問題版本的形式化語言表達。
首先物品的重量 { w i } \{w_i\} {wi?}、收益 { b i } \{b_i\} {bi?}、背包容量$W$和目標值$k$都被編碼為二進制字符串。這里一個整數$m$需要$lo{g}_{2}m$位來表示。
語言$L(Knapsack)$：包含所有存在可行解的背包問題實例的編碼。
存在一個物品的子集，滿足以下條件：
總重量不超過$W$。
總收益至少為$k$。
如果存在這樣的子集，那么這個字符串就屬于$L(Knapsack)$。

1.4 復雜性類

1.4.1 復雜性類$P$

復雜性類$P$是包含所有可以用確定性算法在最壞情況下多項式時間內解決的決策問題。
用形式化語言是$P$包含所有可以被多項式時間算法接受的語言$L(X)$（語言$L(X)$即所有“是”的實例集合）。
這些問題可以在$O(p(n))$時間內解決，其中$p(n)$是關于輸入規模$n$的多項式函數。輸入規模通常用$\mid s\mid$表示，即輸入字符串$s$的長度。
確定性算法是指總是能計算出正確答案的算法。也就是說，存在一個算法$A$，如果$s\in L(X)$，那么在輸入$s$時，算法$A$會在時間$p(\mid s\mid )$內輸出“是”，其中$\mid s\mid$是輸入字符串的長度，$p(?)$是一個多項式函數。

直觀描述為$P=計算機可以快速解決的問題$，也就是這些問題可以通過一個清晰的方法（即多項式時間算法）快速解決。
例如如果一個算法的運行時間是$O(n^2)$或$O(n^3)$，那么它就是多項式時間算法。
現在我們給出復雜性類$P$的幾個問題示例。

1. 分數背包問題（Fractional Knapsack Problem）
2. 帶非負邊權的圖中的最短路徑問題（Shortest Paths in Graphs with Non-negative Edge Weights）
3. 任務調度問題（Task Scheduling）

1.4.2 證明（Certification）

找到決策問題的解決方案可能很難，但是驗證解決方案是相對簡單的。
例如數獨（Sudoku）問題。
數獨問題給定一個$n^2\times n^2$的數組，該數組被劃分為n×n的方塊。數組中的一些單元格已經填入了介于$\mathrm{1...}{n}^2$范圍內的整數。
目標是完成數組，使得每一行、每一列和每個方塊都包含從$\mathrm{1...}{n}^2$的所有整數。
找到數獨問題的解決方案可能很困難，因為需要嘗試不同的組合并滿足所有約束條件。
然而，一旦找到一個解決方案，驗證它是否正確卻相對容易，因為只需要檢查每一行、每一列和每個子網格是否包含從$\mathrm{1...}{n}^2$的所有整數，而不重復。

因此我們現在回到前面的 { 0 , 1 } \{0,1\} {0,1}背包問題。
給定一組物品的重量、收益，以及參數$W$（背包的最大容量）和$k$（目標收益），如果提出一個這些物品的子集，可以很容易地檢查這些物品的總重量是否不超過$W$，以及總收益是否至少為$k$。
如果這兩個條件都滿足，那么我們說這個物品子集是決策問題的一個證明（certificate），即它驗證了 { 0 , 1 } \{0,1\} {0,1}背包決策問題的答案是“是”。
有效證明的概念是用來定義NP問題類的。NP（Nondeterministic Polynomial time）問題類包含所有可以在多項式時間內驗證解的決策問題。

1.4.3 復雜性類NP

NP類包含所有存在有效證明者的決策問題。
這里的“有效證明者”指的是可以在多項式時間內驗證解的算法。更正式的定義如下：
對于一個決策問題$X$，有效證明者是一個算法$B$，它接受兩個輸入字符串$s$和$t$。
字符串$s$是決策問題的輸入。
“有效”意味著$B$是一個多項式時間算法，即存在一個多項式函數$q(?)$，對于所有字符串，我們有$s\in L(X)$當且僅當存在一個字符串$t$，使得$\mid t\mid \le q(\mid s\mid )$且$B(s,t)=“是”$。
這里$\mid t\mid \le q(\mid s\mid )$的意思是：證明$t$的長度必須被一個關于輸入$s$長度的多項式函數$q(?)$所限制。換句話說，那就是證明不會隨著輸入的增長而呈指數級增加。
我們可以將字符串$t$視為決策問題答案為“是”的“證明”。換句話說，如果存在這樣的字符串$t$，那么它就證明了輸入字符串$s$屬于語言$L(X)$。

下面給出例子。
COMPOSITE問題：給定一個整數$s$，判斷$s$是否為合數（即不是質數）。
如果存在一個整數$t$（滿足$1<t<s$），使得$s$是$t$的倍數，那么$s$就是合數。
在這里YES實例$s=437,669$。
我們的證明$t=541或809$。
因為$437,669=541\times 809$。
所以我們回到前面的定義檢查以下，這里$s=437,669\in L(X)$，因為$437,669$是合數。然后我們用$437,669/541$能很快地出結果，這一步的算法是多項式復雜度的。這里有效證明者做的是檢查$t$是否滿足 $1<t<s$并驗證$s$是否能被$t$整除。
我們再舉一個NO實例$s=437,677$。所以我們這里$B(s,t)=“是”$。
對于這個實例，我們不存在任何證明（Certificate）可以欺騙驗證者使其錯誤地判斷該實例屬于語言$L(X)$。

我們現在對YES實例和NO實例有了更清楚的理解。
YES實例：存在一個證明（Certificate），使得驗證者可以確認該實例屬于語言$L(X)$。
NO實例：不存在任何證明（Certificate）可以欺騙驗證者使其錯誤地判斷該實例屬于語言$L(X)$

1.4.4 非確定性算法（non-deterministic algorithm）

非確定性算法是在執行過程中可以執行任意數量的非確定性分支的算法。
這種算法在其中一個分支結束時終止。

非確定性分支指的是算法在某個步驟可以同時探索多個可能的選擇，而不是只選擇一個。
這種選擇不是真正并行執行的，而是一種理論上的構造，用于描述算法可能探索的所有可能路徑。

我們現在給出NP問題類的另一種定義。NP問題類是可以在多項式時間內非確定性地接受（即找到解決方案）的決策問題$X$（或語言$L(X)$）的集合。
非確定性計算機是一種理論上的計算模型，它可以“猜測”正確的答案或解決方案。
NP問題也可以被看作是那些解決方案可以在多項式時間內被驗證的問題類。
對于輸入字符串$s$，非確定性算法可以生成一個多項式長度的字符串$t$（作為解決方案的“證明”或“證書”）。
然后，我們使用算法$B$來檢查$B(s,t)=“是”$。
重要的是，如果答案是“是”，則算法$B$將在多項式時間內以該輸出終止。

現在我們回到我們貫穿始終的例子 { 0 , 1 } \{0,1\} {0,1}背包問題。
給定一組物品 I = { i 1 , i 2 , . . . , i n } I=\{i_1,i_2,...,i_n\} I={i1?,i2?,...,in?}，每個物品$i_j$有一個正整數重量$w_j$和一個整數收益$b_j$。另外，給定一個最大重量$W$和一個整數$k$。
假設有人提出了一個物品的子集，我們可以很容易地檢查（有效驗證者）：

1. 這些物品的總重量是否不超過$W$；
2. 總價值是否至少為$k$。

如果這兩個條件都滿足，那么這個物品子集就是一個證明（certificate）$t$，用于驗證 { 0 , 1 } \{0,1\} {0,1}背包決策問題的答案是“是”。
算法$B(s,t)$=“是”意味著算法$B$接收輸入字符串$s$（表示背包問題的實例）和證明$t$（表示提出的解），并驗證這個解是否正確。
我們需要注意這里輸入$s$表示整個背包問題的實例，包括所有物品的重量集合、所有物品的收益集合、背包的最大容量$W$和目標收益$k$。
而證明$t$表示提出的一個可能的解決方案，即一個物品的子集。
滿足條件的物品子集是可行解，而不是必然是最優解。最優解是指在所有可行解中收益最大的解，這通常涉及到更復雜的計算和比較。
在NP問題的定義中，我們關注的是是否存在至少一個可行解，而不是找到最優解。

所以我們現在再總結一下這里的概念。

1. 算法$A$（決策算法）:
   算法$A$旨在確定輸入$s$是否屬于語言$L(Knapsack)$。
   它通過搜索有效物品子集直接解決問題。
2. 算法$B$（驗證算法）:
   算法$B$是一個驗證器（證明者），用于檢查給定的物品子集$t$（證書）是否是輸入$s$的有效解決方案。
3. 非確定性算法：
   { 0 , 1 } \{0,1\} {0,1}背包問題的非確定性算法涉及猜測一個物品子集并使用算法$B$進行驗證。
4. 證書$t$：
   提出的物品子集，作為輸入$s$屬于$L(Knapsack)$的證據。
5. 輸入字符串$s$：
   $s$是輸入字符串，表示整個背包問題的實例。
6. 語言$L(Knapsack)$：
   包含所有存在可行解的背包問題實例的編碼。

現在我們給出一個例子。
假設我們有一個具體的 { 0 , 1 } \{0,1\} {0,1}背包問題實例，其中包含$3$個物品，每個物品的重量和收益分別為 { 2 , 3 , 4 } \{2,3,4\} {2,3,4} 和 { 3 , 4 , 5 } \{3,4,5\} {3,4,5}，背包的最大容量為$5$，目標收益為$7$。這個實例的二進制編碼可能如下：
$w_1=2$ → 二進制編碼為$10$。
$w_2=3$ → 二進制編碼為$11$。
$w_3=4$ → 二進制編碼為$100$。
$b_1=3$ → 二進制編碼為$11$。
$b_2=4$ → 二進制編碼為$100$。
$b_3=5$ → 二進制編碼為$101$。
$W=5$ → 二進制編碼為$101$。
$k=7$ → 二進制編碼為$111$。
將這些編碼組合成一個字符串，例如：$10,11,100,11,100,101,101,111$。這個字符串$s$就是輸入，它編碼了整個背包問題的實例。而這個$s$屬于$L(Knapsack)$,因為存在$t$滿足$B(s,t)=“是”$。

1.4.5 P和NP的關系：

$P?NP$：P是NP的一個子集。這意味著所有可以在多項式時間內解決的問題（P類問題）也可以在多項式時間內驗證解（因此也是NP問題）。
P問題：可以在多項式時間內解決的問題。這些問題被認為是“容易”的，因為它們可以快速找到解決方案。
NP問題：如果給定一個解決方案，可以在多項式時間內驗證的問題。這些問題可能很難找到解決方案，但如果給定一個潛在的解決方案，可以快速驗證其正確性。
如果一個問題屬于P類（可以在多項式時間內解決），那么它的解決方案也可以在多項式時間內使用相同的算法進行驗證。

$P=NP$還是$P\ne NP$：
這是計算復雜性理論中最著名的未解決問題之一。數學家和計算機科學家目前不知道P是否等于NP，還是P不等于NP。盡管多項式時間內的可驗證性看起來是比多項式時間內的可解性更弱的條件。

2. NP-Completeness（NP完全性）

2.1 布爾電路（Boolean Circuit）

布爾電路是一種有向圖，其中每個頂點（稱為邏輯門）對應于一個簡單的布爾函數，如AND（與）、OR（或）或NOT（非）。
輸入邊（Incoming edges）：指向邏輯門的邊，表示該邏輯門的輸入。
輸出邊（Outgoing edges）：從邏輯門出發的邊，表示該邏輯門的輸出。

示例如下圖所示。

2.2 Circuit-SAT問題

這里SAT 代表可滿足性（Satisfiability）。
輸入：一個具有單個輸出頂點的布爾電路。
問題：是否存在一種輸入值的賦值方式，使得布爾電路的輸出值為$1$？
非確定性算法：非確定性算法選擇一種輸入位的賦值方式，并確定性地檢查這種輸入是否會產生輸出值為$1$。
示例如下圖所示。

這里有多種滿足的結果。

因此Circuit-SAT問題的完整表達是給定一個具有單個輸出節點的布爾電路，是否存在一種輸入值的賦值方式，使得輸出值為$1$？

這里的Circuit-SAT屬于NP問題類的證明如下：
猜測：非確定性算法為所有輸入以及每個邏輯門的輸出猜測值。
驗證：驗證每個邏輯門的輸出（我們猜測的）是否與其基于輸入的布爾函數（AND、OR、NOT）相匹配。這種驗證相對于電路大小在多項式時間內完成。
接受條件：如果所有門都與其布爾函數一致，并且最終輸出為1，則接受該解決方案。
由于解決方案可以在多項式時間內被驗證，因此Circuit-SAT屬于NP問題類。

2.3 頂點覆蓋問題（Vertex Cover，VC）

頂點覆蓋是指給定一個圖$G=(V,E)$，其中$V$是頂點集，$E$是邊集。
頂點覆蓋是$V$的一個子集$C?V$，使得對于$E$中的每條邊$(v,w)$，至少有一個頂點$v$或$w$在$C$中。
圖和頂點覆蓋示例如下。

優化問題版本：尋找盡可能小的頂點覆蓋，即找到一個最小的頂點集合$C$，使得$C$是圖$G$的一個頂點覆蓋。
決策問題版本：給定一個圖$G$和一個整數$k$，詢問是否存在一個包含最多$k$個頂點的頂點覆蓋。

這里的決策問題屬于NP問題類的證明如下：
猜測：一個非確定性算法猜測$V$的一個子集$C$，其大小最多為$k$。這意味著我們從圖$G$中選擇最多$k$個頂點。
驗證：首先檢查$\mid C\mid \le k$。然后驗證對于每條邊$(u,v)\in E$，至少有一個頂點$u$或$v$在$C$中。這種驗證相對于邊的數量在多項式時間內完成。
接受條件：如果$\mid C\mid \le k$并且所有邊都通過了這個檢查，則接受該解決方案。
由于解決方案可以在多項式時間內被驗證，頂點覆蓋問題屬于NP問題類。

2.4 多項式時間可歸約性（Polynomial-time reducibility）

多項式時間可歸約性（Polynomial-time reducibility）對于確定一個問題是否為NP完全問題是重要的。
一個決策問題$L$可以在多項式時間內歸約到另一個多項式時間問題$M$（記作 $L\stackrel{\text{poly}}{\to }M$），如果存在一個可以在多項式時間內計算的函數$f$，滿足以下條件：
將$L$的任何輸入$s$轉換為$M$的輸入$f(s)$。
$s$是$L$的“是”實例當且僅當$f(s)$是$M$的“是”實例。

歸約的意義主要是:

1. 如果$M$可以在多項式時間內解決，那么$L$也可以。
2. 如果$L$是難解的（即沒有已知的多項式時間算法），那么$M$也必須是難解的。
   這兩點都是因為歸約可以證明$M$至少和$L$一樣難。

我們使用$L\stackrel{\text{poly}}{\to }M$表示語言$L$可以在多項式時間內歸約到語言$M$。

2.4.1 NP-hard

如果一個決策問題定義的語言$M$是NP-hard的，那么NP中的每一個其他語言$L$都可以在多項式時間內歸約到$M$。這意味著對于NP中的每一個$L$，都存在一個多項式時間可計算的函數$f$，使得$L\stackrel{\text{poly}}{\to }M$。

如果一個語言$M$是NP-hard的，并且它本身也屬于NP（即可以在多項式時間內解決），那么$M$就是NP完全的（NP-complete）。
NP完全問題是NP中最難的問題之一。如果能夠解決任何一個NP完全問題，那么理論上也能在多項式時間內解決所有NP問題。

P問題：可以在多項式時間內解決的決策問題。形式上，如果一個問題可以在 $O(n^k)$時間內解決，其中$n$是輸入的大小，$k$是某個常數，則該問題屬于P類。
NP問題：給定一個解決方案，可以在多項式時間內驗證其正確性的決策問題。
NP-Hard問題：至少和NP問題中最難的問題一樣難的問題。NP中的每個問題都可以在多項式時間內歸約到NP-Hard問題。值得注意的是，NP-Hard問題可能不屬于NP類，因為它們可能比NP問題更難（例如，停機問題）或者無法在多項式時間內驗證解。
NP-Complete問題：同時滿足以下兩個條件的問題：

1. NP-Hard（所有NP問題都可以歸約到這些問題）。
2. 屬于NP（解決方案可以在多項式時間內被驗證）。

因此，NP完全問題是NP-hard問題集合和NP問題集合的交集。
下面的圖展示了這些問題的關系。

NP完全問題被描述為NP問題類中“最難”的問題。
所以如果一個NP完全問題可以在多項式時間內解決，那么NP中的所有問題都可以在多項式時間內解決，因此P等于NP。

2.5 合取范式（Conjunctive Normal Form，簡稱CNF）

一個布爾公式如果由多個子句（clauses）組成，這些子句使用邏輯與（AND，表示為$\wedge$）連接，而每個子句內部的字面量（literals，即變量$x_i$或其否定 $\overline{x_i}$）使用邏輯或（OR，表示為$\vee$）連接，則稱該公式處于合取范式。
下面給出一些例子。
$(\overline{x_1}\vee \overline{x_2}\vee x_4\vee \overline{x_6})\wedge (\overline{x_2}\vee x_4\vee \overline{x_5}\vee x_3)$

$(x_2\vee \overline{x_3}\vee \overline{x_1})\wedge (x_1\vee x_3\vee x_4)\wedge (\overline{x_4}\vee \overline{x_2}\vee \overline{x_5})$

$(\overline{x_2}\vee x_1)\wedge (\overline{x_1}\vee x_4\vee x_3)\wedge (x_4\vee x_3)\wedge (\overline{x_3}\vee x_2\vee \overline{x_5}\vee \overline{x_1})$

2.6 CNF-SAT（Conjunctive Normal Form Satisfiability）問題

這是布爾可滿足性問題（SAT）的一個特定變體，其中布爾公式以合取范式（CNF）給出。
輸入：一個以合取范式（CNF）表示的布爾公式$C$。
公式$C$由多個子句（clauses）通過邏輯與（AND，表示為$\wedge$）連接組成：$C=c_1\wedge c_2\wedge ...\wedge c_n$，其中每個子句$c_i$是一個字面量（literal）的邏輯或（OR，表示為$\vee$）的組合。每個字面量可以是一個變量$x_k$或其否定$\overline{x_k}$。變量表示為$x_1,x_2,...,x_n$。
問題：是否存在一種布爾值（真/假）的賦值方式給變量$x_1,x_2,...,x_n$ ?
，使得整個公式$C$計算結果為真（即每個子句$c_i$至少有一個字面量為真）？

2.6.1 庫克-列文定理（Cook-Levin Theorem）

庫克-列文定理表明布爾電路可滿足性問題（Circuit-SAT）是NP完全的。
證明過程如下：

步驟1：證明Circuit-SAT屬于NP問題類。
證明：通過計算有限數量的邏輯門的輸出來驗證輸入賦值是否滿足電路，其中之一將是電路的輸出。這可以在多項式時間內完成。因此，根據NP的定義，Circuit-SAT屬于NP。

步驟2：證明Circuit-SAT屬于NP-Hard，所以現在要說明對于NP中的每一個問題 $L$，都存在一個多項式時間可計算的函數，使得$L$可以歸約到Circuit-SAT。
證明：任何NP問題$L$都有一個多項式時間的驗證器$V$（一個圖靈機或算法）。
在輸入$s$和證書$t$上，算法$B$（$V$）的計算可以被編碼為一個布爾電路$C_s$。
歸約：如果$s\in L$，那么存在一個證書$t$使得$C_s(t)=True$。
反之，如果$C_s$是可滿足的，那么$s\in L$。

構建$C_s$的過程需要多項式時間（因為$V$的計算是多項式的）。
因此，Circuit-SAT是NP-Hard的。

所以我們獲得了推論：合取范式可滿足性問題（CNF-SAT）是NP完全（NP-complete）的。
由于任何布爾電路都可以轉換為等價的合取范式（CNF）公式，并且布爾電路可滿足性問題（Circuit-SAT）是NP完全的，因此可以推斷出CNF-SAT也是NP完全的。
這意味著即使在SAT問題的一個受限形式中，即公式以合取范式（CNF）給出時，它仍然是NP-hard的，同時顯然屬于NP。

2.6.2 NP完全性的證明

根據上面的這個定理的證明過程，我們現在知道如何證明一個新的問題$X$是 NP完全的。

1. 首先，證明$X\in NP$：
   這意味著需要展示問題 X 有一個多項式時間的非確定性算法，或者等價地，展示 X 有一個有效的驗證器（certifier）。
   驗證器是一個能在多項式時間內驗證給定解是否正確的算法。
2. 其次，選擇一個已知的 NP完全問題$Y$，并展示從$Y$到$X$的多項式時間歸約：這意味著需要展示$Y\stackrel{\text{poly}}{\to }X$，即對于$Y$中的每個實例，都可以在多項式時間內構造出一個對應的$X$實例，使得$Y$實例的解與$X$實例的解等價。（也就是證明$X$是NP-hard的）

我們現在介紹一個引理，或者說歸約的傳遞性：如果$L_1$可以在多項式時間內歸約到$L_2$，且$L_2$可以在多項式時間內歸約到$L_3$，那么$L_1$也可以在多項式時間內歸約到$L_3$。

現在我們可以嘗試將前面的頂點覆蓋問題（VC）歸約到合取范式可滿足性問題（CNF-SAT）。
證明步驟如下：
對于圖中的每個頂點$i$，引入一個布爾變量$v_i$，如果頂點$v_i$在覆蓋集$C$中，則$v_{=}1i$
對于每條邊$(i,j)\in E$，至少有一個端點必須在覆蓋中。這可以通過子句$(v_i\vee v_j)$來編碼。
整個覆蓋條件是所有這些子句的邏輯與（AND）：$?(i,j)\in E(v_i\vee v_j)$。
我們需要確保頂點覆蓋中頂點的數量最多為$k$。這可以通過使用加法布爾電路（adder Boolean circuits）和等式電路（equality circuits）來完成這個驗證過程。
這種構造可以在多項式時間內完成。

歸約：如果圖$G$有一個大小不超過$k$ 的頂點覆蓋$C$，則設置$v_i=1$對于 $i\in C$，否則$v_i=0$滿足所有邊子句。
反之，一個滿足的賦值給出了一個大小不超過$k$的頂點覆蓋$C=i\mid v_i=1$。

2.6.3 3-SAT（3可滿足性問題）

輸入：一個CNF形式的布爾公式$C=c_1\wedge c_2\wedge ...\wedge c_n$其中子句$c_i$依賴于變量$x_1\wedge x_2\wedge ...\wedge x_m$，并且每個子句$c_i$形式為$x_{i1}\vee x_{i2}\vee x_{i3}$，其中 $1\le i\le m$。
問題：是否存在一種變量$x_i$的真值賦值方式，使得公式$C$可滿足（即最后的結果為真，或者說每個子句的結果都為真）？

3-SAT是CNF-SAT問題的一個特例，其中每個子句恰好包含三個文字量（literals）。
所以3-SAT也是NP完全的。

2.6.4 團問題（Clique問題）

團（Clique）是圖的一個子圖，它是一個完全圖。完全圖是指圖中的每個節點至少通過一條邊與其他所有節點相連。
問題：給定一個圖$G$，問題是判斷$G$中是否存在一個包含$k$個節點的完全子圖（即$k$-團）。
團問題也是NP完全的。

2.6.5 獨立集問題（Independent Set）

給定一個圖$G=(V,E)$，其中$V$是頂點集，$E$是邊集，獨立集$S$是$V$中的一組頂點，這組頂點中任意兩個頂點都不相鄰（即圖中不存在連接這兩個頂點的邊）。
問題：是否存在一個至少包含$k$個頂點的獨立集。
獨立集問題也是NP完全的

2.6.6 NP完全問題的總結

NP完全問題有：

1. { 0 , 1 } \{0,1\} {0,1}背包問題

2. Circuit-SAT問題

3. CNF-SAT問題

4. 3-SAT問題

5. VC問題

6. Clique問題

7. Independent Set問題

8. Feedback Arc Set（反饋弧集）：
   在有向圖中，反饋弧集問題是找到最小的弧集合，移除這些弧后使得圖不再包含任何有向環（即變得無環）。

9. Hamiltonian Cycle（哈密頓回路）：
   哈密頓回路問題是確定一個圖中是否存在一個回路，該回路恰好訪問每個頂點一次并返回起始頂點。

10. Max Cut（最大割）：
    最大割問題是在一個無向圖中找到一個頂點的劃分，使得劃分產生的兩個子圖之間的邊的權重之和最大。

11. Subset Sum（子集和）：
    子集和問題是確定一個整數集合是否有一個子集，其元素之和等于給定的目標和。

12. Integer Programming（整數規劃）：
    整數規劃是線性規劃的一個子類，其中要求解決方案中的變量是整數。這包括了各種優化問題，如找到一組物品的最優組合，滿足特定的約束條件。

還有其他NP完全問題。

2.7 系統證明VC問題是NP完全的

我們現在系統的證明一下VC問題是NP完全的。
證明步驟如下：

步驟1：VC屬于NP。（也就是展示問題有一個多項式時間的非確定性算法，或者等價地，展示問題有一個有效的驗證器）
要證明VC屬于NP，需要展示給定一個候選解（一個頂點的子集$S$），我們可以在多項式時間內驗證$S$是否是大小最多為$k$的頂點覆蓋。
驗證過程：首先檢查$\mid S\mid \le k$：計算$S$中的頂點數量并與$k$比較，這需要 $O(\mid V\mid )$時間。
對于圖中的每條邊$(u,v)\in E$，檢查$u\in S$或$v\in S$：這需要檢查最多$\mid E\mid$條邊，每條邊檢查需要$O(1)$時間。
因此，總的驗證時間是$O(\mid V\mid +\mid E\mid )$，這是多項式時間。
因此，VC屬于NP。

步驟2：從已知的NP完全問題歸約到VC，這里我們使用3-SAT，也就是3-SAT到VC的歸約。
歸約目標：在多項式時間內，構造一個圖和一個頂點數量$k$，使得存在一個大小為$k$的頂點覆蓋當且僅當3-SAT公式可滿足。
對于給定的3-SAT公式$?$，其中包含$m$個子句$C_1,...,C_m$和$n$個變量$x_1,...,x_n$，構造圖$G$的方式如下：
例如我們現在有一個3-SAT公式$?$有兩個變量和三個子句。
$?=(x_1\vee x_2\vee x_2)\wedge (\overline{x_1}\vee \overline{x_2}\vee \overline{x_2})\wedge (\overline{x_1}\vee x_2\vee x_2)$
我們創建一個特殊的子圖結構（Variable Gadget）：
每個變量$x_i$創建兩個頂點$x_i$和$\overline{x_i}$并且用一條邊連接它們。任一頂點覆蓋必須包含至少兩個頂點中的一個頂點以覆蓋這條邊。

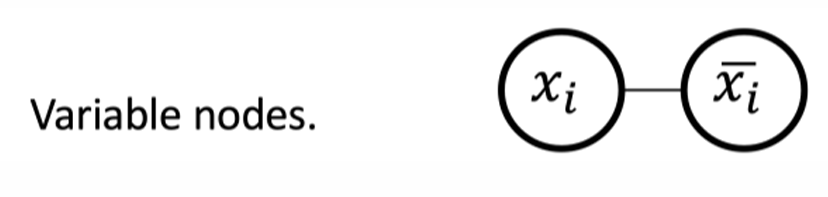
也就是對于每個變量對應的gadget（即每個變量的子圖結構），我們必須恰好選擇一個節點來包含在我們的頂點覆蓋中。

我們再構造另一種特殊子圖（Clause Gadget）：
對于每個子句$C_j=(l_{j_1}\vee l_{j_2}\vee l_{j_3})$，創建一個由三個頂點$v_{j_1},v_{j_2},v_{j_3}$,并連接每個$v_{j_k}$到變量gadget中對應的字面量。（例如如果$l_{i_1}=x_i$，將$v_{j_1}$連接到$x_i$）
如下圖所示。


因此現在對于每一個clause gadget triangle我們需要恰好選擇兩個頂點來覆蓋該三角形的所有邊。

但是我們對于升級的gadget里，如果變量gadget覆蓋了否定。

有一種情況不行。
如果覆蓋的是$x_i$。

只需要1+2三個節點就可以。

我們用直覺稍微解釋一下。
圖中的變量節點（如$x_i$和$\overline{x_i}$）代表SAT問題中的變量及其否定形式。這些節點用于表示布爾變量的賦值。
對于每個子句（clause），根據SAT賦值選擇兩個節點。這些節點代表子句中的文字量（literals）。
如果一個字面量為真，其連接的子句節點不需要被選中。
如果一個字面量為假，其連接的子句節點必須被選中。
每個子句gadget必須至少有一個連接到一個真字面。（如上面的那種情況就不符合）

所以前面的式子所對應構造出來的圖如下圖所示。

根據我們現在前面的結論，對于每個變量，我們需要覆蓋一個節點。對于每個子句我們需要覆蓋兩個節點。因此假設我們現在有$n$個變量和$m$個子句，那么現在需要選擇的節點數$k=n+2m$，因此對于這個例子來說，$k=2+3?2=8$。

現在我們開始說一下如何從3-SAT問題的解構造頂點覆蓋問題的解：
變量選擇（大小$n$）：如果$x_i$為真（true），則在頂點覆蓋中選擇$x_i$，否則選擇$\overline{x_i}$。這確保了變量節點之間的所有邊都被覆蓋。
子句選擇（大小$2m$）：對于每個子句$C_j$，至少有一個字面$l_{j_t}$為真（$t=[1,2,3]$)。選擇與$l_{j_t}$相連的兩個頂點，以確保所有子句邊都被覆蓋。
總的頂點覆蓋大小為$n$（變量）加上$2m$（子句）。
所有的變都會被覆蓋，VC也有會有正確的大小。
如下圖所示。我們取$x_1$為假，$x_2$為真。

對于第一個子句，由于第三個字面也就是$l_{1_3}$為真，所以選擇與其相連的兩個頂點。
對于第二個子句，由于第一個字面也就是$l_{2_1}$為真，所以選擇與其相連的兩個頂點。
對于第三個子句，由于第二個字面也就是$l_{1_3}$為真，所以選擇與其相連的兩個頂點。

那么反過來如何從3SAT到VC呢？
給定條件：給定一個圖$G$有一個大小為$k=n+2m$的頂點覆蓋$S$，其中$n$是變量的數量，$m$是子句的數量。
變量賦值過程:

1. 變量gadget處理：
   對于每個變量gadget（每個變量及其否定形式對應的兩個頂點），頂點覆蓋集合$S$中必須恰好有一個頂點被選中。
   如果$x_i$被選中（即$x_i\in S$），則將∈S的值設為真（true）。
   如果$\overline{x_i}$被選中（即$\overline{x_i}\in S$），則將∈S的值設為假（false）。
2. 子句gadget處理：
   對于每個子句gadget（每個子句對應的三角形），未選中的節點$v_{j_t}$必須連接到$l_{j_t}$的頂點gadget，而這個$l_{j_t}（x_i)$的值為真，否則這條邊$(v_{j_t},x_i)$不會被覆蓋。
   因此對于每個子句，至少有一個字面為真，從而滿足3-SAT公式$?$。

圖的構造：

1. 變量節點：
   對于3-SAT問題中的每個變量$n$，圖中創建兩個頂點，分別代表該變量及其否定形式。這會產生$2n$個頂點。
   每個變量gadget（變量及其否定形式）之間有一條邊相連，表示在頂點覆蓋中，變量及其否定形式不能同時被選中。
2. 子句節點：
   對于3-SAT問題中的每個子句$m$，圖中創建一個包含三個頂點的三角形，代表子句中的三個字面量。這會產生$3m$個頂點。
   每個子句gadget中的頂點連接到變量gadget中對應的字面，表示在頂點覆蓋中，至少有一個字面需要被選中。一共為$3m$條邊。
   所以一共：
3. 頂點：
   變量gadget產生的頂點：$2n$
   子句gadget產生的頂點：$3m$
   總頂點數量：$2n+3m$
4. 邊：
   變量gadget產生的邊：$n$（每個變量gadget有一條邊）
   子句gadget內部的邊：$3m$（每個子句gadget有三個頂點，形成三角形，有三條邊）
   子句gadget與變量gadget的連接邊：$3m$（每個子句gadget的三個頂點分別連接到三個變量gadget）
   總邊數量：$n+3m+3m=n+6m$

因此算法復雜度為$O(n+m)$，所以從3-SAT問題構造VC問題的圖的過程可以在多項式時間內完成，這意味著這種歸約是有效的。

3. 優化問題（Optimization Problems）

說完決策問題，我們說優化問題。優化問題（Optimization problems）中我們的目標是最大化或最小化某個值。
即我們有一個問題實例$x$，它有許多可行的“解決方案”。我們試圖最小化（或最大化）某個成本函數$c(S)$，其中$S$是問題實例$x$的一個“解決方案”。
例如：

1. 最小生成樹（Minimum Spanning Tree）
2. 最小頂點覆蓋（Smallest Vertex Cover）

系統一點的定義如下：
對于解決方法我們有一個可行解集（Feasible solution）：對于每個問題實例$x$，我們有一組可行解$F(x)$。這些解滿足問題的所有約束條件。
成本函數（Cost function）：每個可行解$s\in F(x)$都有一個成本$c(s)$。成本函數衡量解的優劣或效率。
最優成本（Optimum cost）：最優成本$OPT(x)$定義為所有可行解中成本函數的最小值（或最大值，取決于是最小化還是最大化問題）： O P T ( x ) = m i n { c ( s ) : s ∈ F ( x ) } OPT(x)=min\{c(s):s∈F(x)\} OPT(x)=min{c(s):s∈F(x)}（或$max$）。

許多計算問題都是NP完全優化問題。例如：尋找具有最小節點數的頂點覆蓋。

3.1 近似比率（Approximation Ratio）

因此面對NP完全性問題我們要試著尋找盡可能好的解決方案。
那如何衡量解決方案的“好”呢？近似比率（approximation Ratio）是衡量解決方案質量的一個常用方法。
假設我們有一個算法，它為問題實例$x$返回一個解決方案$T(x)$。
一種衡量解決方案質量的方法是比較算法找到的解決方案$T(x)$ 的成本$c(T(x))$與最優解$OPT(x)$的成本$c(OPT(x))$的比率。
近似算法為優化問題產生一個解$T$。
$T$是最優解$OPT$的$k$-近似，如果$c(T)/c(OPT)\le k$（對于最小化問題）。
$T$是最優解$OPT$的$k$-近似，如果$c(OPT)/c(T)\le k$（對于最大化問題）。
這里，$c(T)$是算法找到的解的成本，$c(OPT)$是最優解的成本。$k$的值永遠不會小于$1$。
$1$-近似算法意味著找到的解就是最優解($k=1$，代表就是最優解）。
我們的目標是找到一個多項式時間的近似算法，具有較小的常數近似比率。

3.2 多項式時間近似方案（Polynomial-Time Approximation Schemes，簡稱PTAS）

近似方案是一種近似算法，它接受一個參數$\epsilon >0$作為輸入，使得對于任何固定的 $\epsilon >0$，該方案是一個$(1+\epsilon )$-近似算法。
這意味著算法找到的解的成本與最優解$OPT$的成本之間的比率不超過$1+\epsilon$。

如果一個問題$L$有一個多項式時間的$(1+\epsilon )$-近似算法，對于任何固定的$\epsilon >0$，那么$L$有一個多項式時間近似方案（PTAS）。
這里的$(1+\epsilon )$-近似算法意味著算法找到的解的成本不超過最優解成本的$1+\epsilon$倍。

隨著$\epsilon$的減小，算法的運行時間可能會迅速增加。這是因為更小的$\epsilon$值意味著需要更精確的解，這可能需要更多的計算資源。
例如，算法的運行時間可能是$O(n^{2/\epsilon })$

3.3 完全多項式時間近似方案（Fully Polynomial-Time Approximation Schemes，簡稱FPTAS）

當一個近似方案的運行時間是多項式，不僅與問題實例的大小$n$成正比，而且與 $1/\epsilon$也成正比時，我們稱其為完全多項式時間近似方案（FPTAS）。
例如，算法的運行時間可能是$O((1/\epsilon {)}^3{n}^2)$

3.4 頂點覆蓋問題

我們現在再回到頂點覆蓋問題。
頂點覆蓋是頂點集 V 的一個子集$C?V$，滿足對于$E$中的每條邊$(u,v)$，至少有一個頂點$u$或$v$在$C$中，或者兩個頂點都在$C$中。這意味著$C$中的頂點“覆蓋”了圖中的每一條邊。
所以現在關于頂點覆蓋的優化問題OPT-VERTEX-COVER問題是給定一個圖$G$，找到$G$的一個頂點覆蓋，其大小盡可能小。
OPT-VERTEX-COVER問題是一個NP-hard問題。

3.4.1 關于頂點覆蓋問題的近似算法

偽代碼如下：

也就是在現在圖中選擇任意一條邊，將這條邊的兩個端點$u$和$v$添加到頂點覆蓋中。再移除所有與$u$或$v$相關的邊（即所有以$u$或$v$為端點的邊）。然后循環這個過程。

下面我們看一個例子，如圖所示。

現在我們假設選擇 { b , c } \{b,c\} {b,c}，所以我們將這兩個頂點添加到覆蓋中，并將所有相鄰的邊去掉。

然后我們選擇 { e , f } \{e,f\} {e,f}，所以我們將這兩個頂點添加到覆蓋中，并將所有相鄰的邊去掉。

然后我們選擇 { d , g } \{d,g\} {d,g}，所以我們將這兩個頂點添加到覆蓋中，并將所有相鄰的邊去掉。

沒有邊剩余，所以這就是近似算法的結果。
下圖的左邊是我們得出的近似算法結果，右邊是最優解結果。

這個算法是2-近似的，我們需要找到一個下界（lower bound）來估計最優解$C^{?}$的大小。
證明如下：
$A$是算法第4行選擇的邊的集合。這些邊是在算法的迭代過程中被選中的，用于構建頂點覆蓋。
任何頂點覆蓋必須覆蓋集合$A$中每條邊至少一個端點。這是因為頂點覆蓋的定義要求圖中的每條邊至少有一個端點在頂點覆蓋中。
集合$A$中的任意兩條邊不共享一個頂點。這是因為對于$A$中的任意兩條邊，其中一條必須先被選中（第4行），然后在第6行中，所有與已選中邊共享頂點的邊將從邊集$E^{\prime }$中刪除，因此它們在下一次迭代中不再被考慮。
為了覆蓋集合$A$，最優解$C^{?}$必須至少包含與$A$中邊數一樣多的頂點。這是因為每條邊至少需要一個頂點來覆蓋，所以最優解的大小至少是$\mid A\mid$。即$\mid A\mid \le |C^{?}|$
算法的第4行選擇一條邊，這條邊的兩個端點都不在當前的頂點覆蓋集合$C$中。
第5行將這條邊的兩個端點添加到$C$中。所以我們可以知道$\mid C\mid =2\mid A\mid$，其中$A$是算法選擇的所有邊的集合。
因此$\mid C\mid \le 2|C^{?}|$。這意味著算法找到的頂點覆蓋$C$的大小不會超過最優解$C^{?}$的兩倍。
由于$\mid C\mid$不能大于最優解的兩倍，所以這是一個頂點覆蓋問題的$2$-近似算法。

在近似算法的證明中，我們通常不知道最優解的大小，但我們可以通過設置一個下界來估計最優解的大小。
通過將找到的解與這個下界關聯，我們可以證明算法的近似比率。

3.4.2 面對NP-hard優化問題的策略

我們可以使用以下策略：

1. 使用已知的指數算法并限制在小規模問題上：
   指數算法的運行時間隨著輸入大小呈指數增長，對于大規模問題來說非常慢。如果問題規模較小，可能還可以使用這類算法。
2. 找出是否可以將問題限制到已知多項式時間解決方案的特殊情況：
   有時可以通過限制問題到特定情況來簡化問題，從而找到多項式時間的解決方案。
   例如，頂點覆蓋問題在二分圖中可以在多項式時間內解決。
3. 放棄最優解，尋找或設計一個提供“足夠好”結果的近似算法：
   近似算法旨在找到接近最優解的解，而不是最優解本身。
   設計一個使用啟發式（heuristic）的聰明近似算法。啟發式是一種基于經驗和直覺的解決問題的方法，它可能不保證找到最優解，但通常能找到足夠好的解。（例如我們前面介紹的定點覆蓋問題的近似解）
   幸運地證明隨機選擇一個解已經足夠好。