二叉樹思想草稿

二叉樹解體兩種思路

  1. 是否可以通過遍歷一遍二叉樹得到答案？
    • 用一個traverse函數配合外部變量
    • 實現遍歷的思維模式
  2. 是否可以定義一個遞歸函數，通過子樹的答案推導出原問題的答案？ 遞歸三部曲：
    • 函數定義，參數，返回值，充分利用返回值
    • 終止條件？
    • 單次遞歸條件？

快速排序：

  • 對于nums[lo…hi]
  • 找到分界點p
  • 通過交換元素使得nums[lo…p-1]都小于nums[p]
  • nums[p+1…hi]都大于nums[p]
  • 然后遞歸處理nums[lo…p-1]和nums[p+1…hi]
  • 最后整個數組就被排序了
void sort(int nums[], int st, int ed) {if (st >= ed) {return;}// ****** 前序位置 ******// 對 nums[lo..hi] 進行切分，將 nums[p] 排好序// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]int p = partition(nums, st, ed);// 左右子數組進行拆分sort(nums, st, p-1);sort(nums, p+1, ed);

先構造分界點，然后去左右子數組遞歸構造分界點，這就是二叉樹的前序遍歷！

歸并排序：

  • 若要對nums[st…ed]排序
  • 先對nums[st…mid]排序
  • 再對nums[mid+1…ed]排序
  • 最后連接兩個有序子數組
void sort(int[] nums, int st, int ed) {if (st == ed) {return;}int mid = (st + ed) / 2;sort(nums, st, mid);sort(nums, mid+1, ed);// ****** 后序位置 ******// 此時兩部分子數組已經被排好序// 合并兩個有序數組，使 nums[lo..hi] 有序merge(nums, st, mid, ed);
}

先對左右子數組進行排序，然后合并，這就是二叉樹后續遍歷框架！并且也是傳說中的分治算法。

二叉樹遍歷方式

  • 遞歸遍歷
  • 層序遍歷

二叉樹遞歸遍歷(DFS)

遞歸遍歷二叉樹代碼模板：

// 定義二叉樹節點
class TreeNode {
public:int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 二叉樹遞歸遍歷框架
void traverse(TreeNode* root) {if (root == nullptr) {return;}traverse(root->left);traverse(root->right);
}

  • traverse函數的遍歷就是一直往左子節點走，直到遇到空指針走不了了，才嘗試往右子節點走，如此循環，直到左右子樹都走完了才返回上一層父節點。

  • 遞歸遍歷節點的順序僅取決于左右子節點的遞歸調用順序，與其他代碼無關。

理解前中后序遍歷

遞歸遍歷的順序，即函數traverse訪問節點的順序是固定的，root指針在樹上移動的順序是固定的。

但是，我們在traverse函數不同位置寫入代碼處理邏輯，產生的效果是不同的，這就是前中后序遍歷的結果不同，原因在于我們把代碼寫在了不同位置，產生了不同效果。

// 二叉樹遍歷框架
void traverse(TreeNode* root) {if (root == nullptr) {return;};// 前序位置traverse(root->left);// 中序位置traverse(root->right);// 后序遍歷位置
}

強調：

  • 三種代碼寫入位置的關鍵區別在于執行時機不同
  • 真正的算法體不會叫我們簡單計算前中后序遍歷結果，而是要我們把正確的代碼寫入到正確的位置上
  • 所以必須準確理解三個位置的代碼產生的不同效果

補充：

  • 二叉搜索樹（BST）的中序遍歷結果是有序的

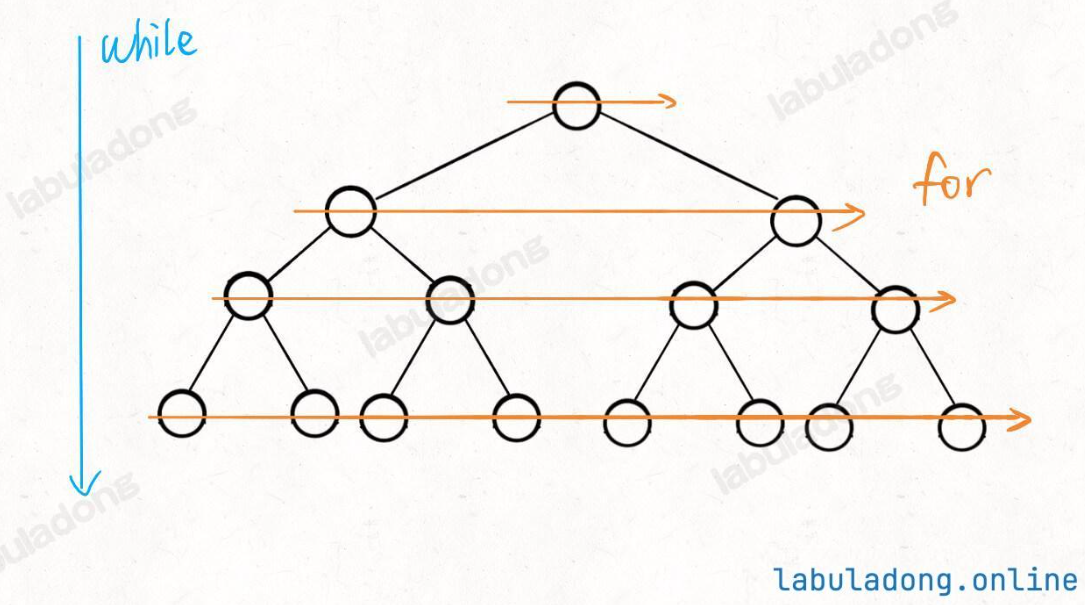
層序遍歷

在這里插入圖片描述

寫法一：

  • 簡單寫法，每次把對頭元素拿出來，然后左右子節點加入隊列
  • 缺點：無法知道節點在第幾層，這是常見需求
  • 這個寫法用得不多
void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}std::queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* cur = q.front();q.pop();// 訪問cur節點// 左右子樹加入隊列if (cur->left != nullptr) {q.push(cur->left);}if (cur->right != nullptr) {q.push(cur->right);}}
}

寫法二：

void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}std::queue<TreeNode*> q;q.push(root);// 記錄當前遍歷到的層數（根節點視為第1層）int depth = 1;while (!q.empty()) {// 記錄當前層的節點數量int sz = q.size();// 處理當前層的所有節點, sz 個// for (int i = 0; i < sz; i++) {while (sz-- > 0) {TreeNode* cur = q.front();q.pop();// 訪問或者處理cur節點...cout << "depth = " << depth << ", val = " << cur->val << endl;// 左右子樹加入隊列if (cur->left != nullptr) {q.push(cur->left);}if (cur->right != nullptr) {q.push(cur->right);}		}depth++;}
}
  • 注意

寫法三：

假設樹枝有不同權重！

class State {
public:TreeNode* node;int depth;State(TreeNode* node, int depth) : node(node), depth(depth) {}
};void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}queue<State> q;// 根節點的路徑權重和是 1q.push(State(root, 1));while (!q.empty()) {State cur = q.front();q.pop();// 訪問 cur 節點，同時知道它的路徑權重和cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;// 把 cur 的左右子節點加入隊列if (cur.node->left != nullptr) {q.push(State(cur.node->left, cur.depth + 1));}if (cur.node->right != nullptr) {q.push(State(cur.node->right, cur.depth + 1));}}
}

深入理解前中后序遍歷

  1. 前中后序遍歷都是什么？
  2. 后序遍歷有何特殊之處？
  3. 為什么多叉樹沒有中序遍歷？

回顧二叉樹遞歸遍歷框架：

// 二叉樹的遍歷框架
void traverse(TreeNode* root) {if (root == nullptr) {return;}// 前序位置traverse(root->left);// 中序位置traverse(root->right);// 后序位置
}
  • 暫且不管前中后序的東西，單單看traverse函數
  • 實質上是個能夠遍歷二叉樹節點的函數
  • 本質上和遍歷數組，鏈表完全一樣
// 迭代遍歷數組
void traverse(vector<int>& arr) {for (int i = 0; i < arr.size(); i++) {}
}// 遞歸遍歷數組
void traverse(vector<int>& arr, int i) {if (i == arr.size()) {return;}// 前序位置traverse(arr, i + 1);// 后序位置
}// 迭代遍歷單鏈表
void traverse(ListNode* head) {for (ListNode* p = head; p != nullptr; p = p->next) {}
}// 遞歸遍歷單鏈表
void traverse(ListNode* head) {if (head == nullptr) {return;}// 前序位置traverse(head->next);// 后序位置
}
  • 可見單鏈表和數組一般遍歷方式是迭代，即for循環或者while循環的方式顯示的迭代
  • 但是也是可以遞歸遍歷的
  • 最關鍵的：只要是遞歸遍歷，都有前序位置和后序位置，分別在遞歸之前和遞歸之后兩個 位置
  • 前序位置：剛進入一個節點時
  • 后序位置：即將離開一個節點時

比如倒序打印一條單鏈表：

void traverse(ListNode* head) {if (head == nullptr) {return;}traverse(head->next);// 在后序位置 執行打印，就可以實現 先遞歸，每次遞歸過去想打印時都要先執行遞歸下一個節點// 直到最后一個節點，遞歸不了，就開始從最后一個節點開始向前打印cout << head->val << endl;
}

  • 前中后序絕不僅僅是三個順序不同的list，而是遞歸遍歷二叉樹過程中，處理每個節點的三個特殊時間點。

  • 前序位置的代碼：在剛剛進入一個二叉樹節點時執行

  • 后序位置的代碼：在即將離開一個二叉樹節點時執行

  • 中序位置的代碼：在一個二叉樹節點的左子樹都遍歷完，即將開始遍歷右子樹的時候開始執行

  • 本文一直視“前中后序”為“位置”，代碼執行位置，執行時機

  • 而不是我們常說的“前中后序”為“遍歷”

兩種解題思路：

  • 遍歷一遍二叉樹得出答案——>回溯算法思想
  • 分解問題，遞歸得到答案——>動態規劃思想

個人函數命名習慣：

  1. 遍歷二叉樹解題時：
    • 函數簽名一般使用void traverse(…)，沒有返回值
    • 靠外部變量來計算結果
    • 與此對應：回溯算法的函數簽名一般也不需要返回值
  2. 分解問題思路解題：
    • 視具體函數，一般會有返回值
    • 返回值是子問題的計算結果
    • 與此對應：動態規劃給出的函數簽名是帶有返回值的dp函數

二叉樹深度

遍歷的思路

  • 遍歷一遍二叉樹 + 外部變量記錄每個節點所在深度
  • 取得最大值就是最大深度
class Solution {// 外部變量記錄當前深度和最大深度int depth = 0;int res = 0;public:// 本題函數簽名, 求取當前樹root的最大深度int maxDepth(TreeNode* root) {return res;}// 遍歷二叉樹求最大深度, void類型簽名, 不返回值void traverse(TreeNode* root) {if (root == nullptr) {return;}// 由于根節點算作深度為1, 所以在前序位置depth++depth++;// 在前序位置, 進入一個新節點時候, 若為葉子節點, 記錄答案if (root->left == nullptr && root->right == nullptr) {res = std::max(res, deqth);}traverse(root->left);traverse(root->right);// 后序位置 是 離開當前節點的時機// 減少深度, 類似回溯, 需要把深度還回去depth--; }
};
  1. 為什么需要前序位置depth++， 后序位置depth–？
    • 把traverse視作一個在二叉樹上游走的指針
    • 前序位置：剛進入一個節點時
    • 后序位置：即將離開一個節點
  2. 對于res的更新？
    • 其實放在前中后序位置都可以
    • 只要保證進入節點之后，離開節點之前

分解+遞歸的思路

class Solution {
public:// 函數簽名：輸入一個根節點root, 返回二叉樹最大深度int maxDepth(TreeNode* root) {// 僅一個節點的深度視為1, 空節點就0if (root == nullptr) return 0;// 當前root的深度等于左右子樹深度較大的一個+1// 分解問題：root的結果依賴 左右子樹的結果int leftMax = maxDepth(root->left);int righMax = maxDepth(root->right);return 1 + std::max(leftMax, rightMax);}
}
  1. 這道題主要代碼思路放在了前中后哪個位置?
    • 后序位置！
    • 后序位置執行深度加的操作！先遍歷了左右子樹，得到結果后，后序位置執行深度加的操作！
二叉樹前序遍歷

遍歷思路

  • 前序位置：執行加vector操作，前序遍歷
  • void簽名函數，無返回值
  • 配合外部變量res
// 遍歷思路計算前序遍歷結果
class Solution {
public:// 外部變量存放前序遍歷結果vector<int> res;// 前序遍歷輸出結果函數簽名vector<int> preorderTraversal(TreeNode* root) {traverse(root);return res;}// 二叉樹遍歷函數, 前序位置執行關鍵操作void traverse(TreeNode* root) {if (root == nullptr) return;// 前序位置res.push_back(root->val);traverse(root->left);traverse(root->right);}
};
  • 這種遍歷思路+外部變量的思路很好想
  • 考慮改成分解問題+遞歸的思路？來得到前序遍歷的結果！

分解思路

  • 前序遍歷的特點：根節點排在首位，接著是左子樹遍歷的結果，最后是右子樹的遍歷結果。
  • 這就實現了分解問題
    • 一個二叉樹前序遍歷結果 = 根節點 + 左子樹前序遍歷結果 + 右子樹前序遍歷結果
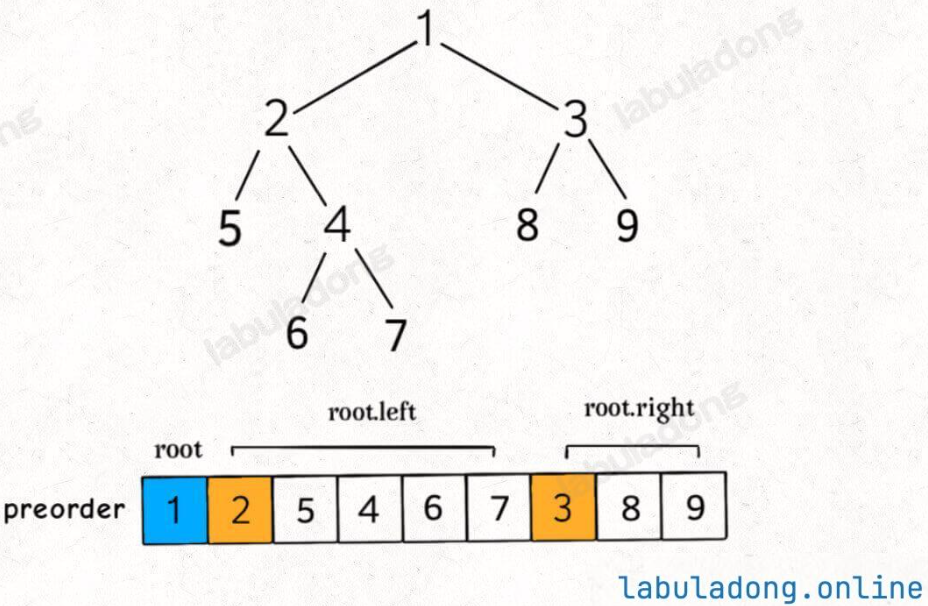
      在這里插入圖片描述
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;// 空節點返回if (root == nullptr) return res;// 前序遍歷的結果 = [root-val , 左子樹前序遍歷結果 , 右子樹前序遍歷結果]	res.push_back(root->val);// vector<int> left = preorderTraversal(root->left);res.insert(res.end(), left.begin(), left.end());vector<int> right = preorderTraversal(root->right);res.insert(res.end(), left.begin(), left.end());	return res;}
};

遇到一道二叉樹題目：

  1. 是否可以通過遍歷一遍二叉樹得到答案？
    • 用一個遍歷函數traverse()，注意前中后序位置的利用
    • 配合外部變量
  2. 是否可以通過定義一個遞歸函數，通過子問題（子樹）的答案推導出原問題的答案？
    • 寫出遞歸函數定義
    • 充分利用函數返回值
  3. 無論哪種思路，最重要的是明白二叉樹中每個節點做什么，在什么時機（前中后序）做？

后序位置的特殊之處

  • 前序位置本身沒啥特殊之處，一般是習慣把前中后序位置不敏感的代碼放在前序位置了。
  • 中序位置主要用在BST場景，完全可以把BST的中序遍歷認為是遍歷有序數組。

仔細觀察前中后位置的代碼：

  • 前序位置的代碼只能從函數參數中獲取父節點傳遞來的數據。
  • 中序位置的代碼不僅有參數數據，還有左子樹通過函數返回值傳遞回來的數據。
  • 后序位置的代碼最強大，不僅獲取參數數據，還可以同時獲得左右子樹通過函數返回值傳遞回來的數據。

所以，某些情況下把代碼移動到后序位置效率最高；
有時，只有后序位置的代碼能做。

舉個例子感受它們能力差別

  1. 如果根節點視作第一層，打印每個節點所在層數
  2. 打印每個節點左右子樹各有多少節點
// 二叉樹遍歷函數
void traverse(TreeNode* root, int level) {if (root == nullptr) return;// 前序位置printf("節點 %s 在第 %d 層", root.val, level);traverse(root->left, level + 1);traverse(root->right, level + 1);
}
// 這樣調用
traverse(root, 1);在這里插入代碼片

// 定義：輸入一棵二叉樹，返回這棵二叉樹的節點總數
int count(TreeNode root) {if (root == null) {return 0;}int leftCount = count(root.left);int rightCount = count(root.right);// 后序位置printf("節點 %s 的左子樹有 %d 個節點，右子樹有 %d 個節點",root, leftCount, rightCount);return leftCount + rightCount + 1;
}
  • 一個節點在第幾層，我們從根節點遍歷過來的過程就能順帶記錄，且遞歸函數的參數就能傳遞下去
  • 而以一個節點為根的整顆子樹有多少節點，必須遍歷完子樹之后才能得到
  • 只有后序位置才能通過返回值獲取子樹的信息！
  • 一旦發現題目與子樹有關，大概率要給函數設置合理的定義和返回值，在后序位置寫關鍵代碼，利用子樹的信息了！

二叉樹直徑

  • 關鍵理解：直徑長度 = 每個節點左右子樹最大深度之和
  • 直徑可以不經過根節點
  • 要求最長直徑長度，那就是遍歷整棵樹每個節點，然后通過每個節點的左右子樹的最大深度，求出每個節點的直徑，最后把直徑取最大值即可

思路一：

class Solution {
public:// 全局變量記錄最大直徑長度int maxDiameter = 0; // 解題主簽名int diameterOfBinaryTree(TreeNode* root) {// 對每個節點計算直徑，求最大直徑traverse(root);return maxDiameter;}private:// 遍歷二叉樹void traverse(TreeNode* root) {if (root == nullptr) return;// 前序位置// 直徑 = 左右子樹各自最大深度之和，所以這里先算左右子樹最大深度int leftMax = maxDepth(root->left);int rightMax = maxDepth(root->right);int myDiameter = leftMax + rightMax;// 更新全局最大直徑		maxDiameter = max(maxDiameter, myDiameter);traverse(root->left);traverse(root->right);}// 計算二叉樹的最大深度int maxDepth(TreeNode* root) {if (root == nullptr) return 0;// 分解問題+遞歸思路int leftMax = maxDepth(root->left);int rightMax = maxDepth(root->right);return 1 + max(leftMax, rightMax);}
};
  • 缺陷很明顯的解法，最壞時間復雜度是 O(N^2)
  • 因為traverse遍歷每個節點（計算直徑）時，還會調用遞歸函數maxDepth，maxDepth同樣遍歷所有子樹的所有節點
  • 究其原因在于，前序位置無法獲取子樹的信息，只能讓每個節點調用maxDepth函數去計算子樹的深度，屬于想起來容易，實現起來容易，但是時間復雜度過高的解法！
  • 如何優化呢？maxDepth的后序位置是已經知道左右子樹的最大深度的，所以將計算直徑的邏輯同樣放在后序位置，放在已知左右子樹最大深度的位置就可以優化時間復雜度。
class Solution {
public:// 全局變量記錄最大直徑長度int maxDiameter = 0; // 解題主簽名int diameterOfBinaryTree(TreeNode* root) {// 對每個節點計算直徑，求最大直徑maxDepth(root);return maxDiameter;}private:// 這樣就不用traverse()單獨計算直徑了！// 去掉traverse()// 計算二叉樹的最大深度int maxDepth(TreeNode* root) {if (root == nullptr) return 0;// 分解問題+遞歸思路int leftMax = maxDepth(root->left);int rightMax = maxDepth(root->right);// maxDepth的后序位置在此，此處已知左右子樹各自的最大深度，這里更新直徑就可以了！int myDiameter = leftMax + rightMax;maxDiameter = max(maxDiameter, myDiameter)return 1 + max(leftMax, rightMax);}
};
  • 時間復雜度只有 maxDepth 函數的 O(N) 了。
  • 遇到子樹問題，首先想到的是給函數設置返回值，然后在后序位置做文章！

思考題：運用后序位置的題目使用的是遍歷思路還是分解問題的思路？

我個人答案：是分解問題的思路，利用了子樹返回的答案，作為當前節點的答案的一部分
看了答案：利用后序位置的題目，一般都使用分解問題的思路，因為當前 節點接收并且利用了子樹返回返回的信息，意味著把原問題分解成了當前節點+左右子樹的子問題。

所以，如果一開始寫出遞歸套遞歸的解法，大概率要反思，重寫成后序遍歷優化！

以樹的視角看動規/回溯/DFS算法的區別和聯系

DFS和回溯算法非常相似，細節上有所區別：

  • DFS 做選擇和撤銷選擇是在for循環外部
  • 回溯 做選擇和撤銷選擇是在for循環內部

結合二叉樹，動歸/DFS/回溯可以看作二叉樹問題擴展，只是關注點不同：

  • 動態規劃算法屬于分解問題、分治的思路，關注點在于整顆子樹，處理子樹的方式和利用子樹返回的結果。
  • 回溯算法屬于遍歷的思路，關注點在于節點之間的樹枝。
  • DFS算法屬于遍歷的思路，關注點在于單個節點處理。

例子一：分解問題的思想體現，動歸
給一個二叉樹，用分解問題的思路寫一個count函數，計算共有多少節點

  • 后序位置，可以利用上左右子樹的返回的結果！
  • 所以后序位置天然與分解的思路適配！
// 函數簽名：輸入一顆二叉樹，返回二叉樹節點總數
int count(TreeNode* root) {if (root == nullptr) return 0;// 分解思路：當前節點下的樹的總節點數 == 左 + 右 + 1int leftCount = count(root->left);int rightCount = count(root->right);// 后序位置：已經得到了左右子樹的結果！return leftCount + rightCount + 1;
}
  • 動態規劃分解問題的思路
  • 著眼點永遠是結構解法相同的整個子問題！
  • 類比到二叉樹上就是遞歸處理子樹
  • 注意后序位置才可以充分利用處理好的子樹結果！

類比一個經典動歸：
斐波那契

// f(n) 計算第 n 個斐波那契數
int fib(int n) {// base case if (n == 0 || n == 1) return n;// fib() 調用 本身是分解問題return fib(n - 1) + fib(n - 2);
}

例子二：回溯算法思想
（這里是java， 請豆包幫我換成cpp的）

void traverse(TreeNode root) {if (root == null) return;printf("從節點 %s 進入節點 %s", root, root.left);traverse(root.left);printf("從節點 %s 回到節點 %s", root.left, root);printf("從節點 %s 進入節點 %s", root, root.right);traverse(root.right);printf("從節點 %s 回到節點 %s", root.right, root);
}
  • 總之對于回溯來說，
    • 在對某個子路徑調用遞歸函數traverse()遍歷之前，就是即將進入時刻，屬于該路徑的前序
    • 在對某個子路徑調用遞歸函數traverse()遍歷之后，就是退出這個節點，回溯時刻！屬于該路徑后序么？（不確定這句話對不對，豆包幫我改！）

把二叉樹進化成多叉樹：（java 改成cpp！）

// 多叉樹節點
class Node {int val;Node[] children;
}void traverse(Node root) {if (root == null) return;for (Node child : root.children) {printf("從節點 %s 進入節點 %s", root, child);traverse(child);printf("從節點 %s 回到節點 %s", child, root);}
}

從這個多叉樹的遍歷框架可以延伸出回溯算法框架套路：

void backtrack(...) {// base caseif (...)  return;for (int i = 0; i < ...; i++) {// 做選擇...// 進入下一層決策樹backtrack(...);// 撤銷剛才的決策...}
}

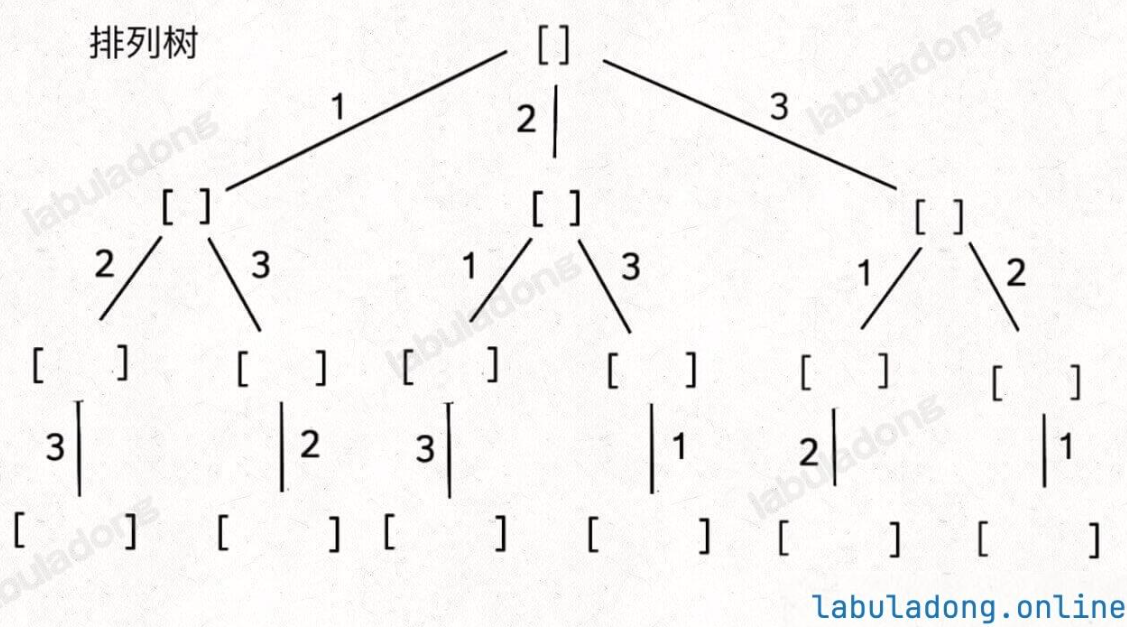
回溯算法關注點是樹的一條條樹枝！
(改cpp)

// 回溯算法核心部分代碼
void backtrack(int[] nums) {// 回溯算法框架for (int i = 0; i < nums.length; i++) {// 做選擇used[i] = true;track.addLast(nums[i]);// 進入下一層回溯樹backtrack(nums);// 取消選擇track.removeLast();used[i] = false;}
}

在這里插入圖片描述
例子三：DFS的思想體現，著眼于節點處理
一棵二叉樹，請你寫一個 traverse 函數，把這棵二叉樹上的每個節點的值都加一。，代碼如下：

void traverse(TreeNode* root) {if (root == nullptr) return;// 遍歷過的每個節點的值加一root->val++;traverse(root->left);traverse(root->right);
}

看具體的 DFS 算法問題，比如
一文秒殺所有島嶼題目 中講的前幾道題，我們的關注點是 grid 數組的每個格子（節點），我們要對遍歷過的格子進行一些處理，所以我說是用 DFS 算法解決這幾道題的：

// DFS 算法核心邏輯
void dfs(int[][] grid, int i, int j) {int m = grid.length, n = grid[0].length;if (i < 0 || j < 0 || i >= m || j >= n) {return;}if (grid[i][j] == 0) {return;}// 遍歷過的每個格子標記為 0grid[i][j] = 0;dfs(grid, i + 1, j);dfs(grid, i, j + 1);dfs(grid, i - 1, j);dfs(grid, i, j - 1);
}

總的來說：

  • 動態規劃關注整顆子樹
  • 回溯關注節點之間的樹枝
  • DFS關注單個節點

理解為什么回溯算法和 DFS 算法代碼中「做選擇」和「撤銷選擇」的位置不同了，看下面兩段代碼：

// DFS 算法把「做選擇」「撤銷選擇」的邏輯放在 for 循環外面
void dfs(Node* root) {if (!root) return;// 做選擇printf("enter node %s\n", root->val.c_str());for (Node* child : root->children) {dfs(child);}// 撤銷選擇printf("leave node %s\n", root->val.c_str());
}// 回溯算法把「做選擇」「撤銷選擇」的邏輯放在 for 循環里面
void backtrack(Node* root) {if (!root) return;for (Node* child : root->children) {// 做選擇printf("I'm on the branch from %s to %s\n", root->val.c_str(), child->val.c_str());backtrack(child);// 撤銷選擇printf("I'll leave the branch from %s to %s\n", child->val.c_str(), root->val.c_str());}
}

回溯算法必須把「做選擇」和「撤銷選擇」的邏輯放在 for 循環里面，否則怎么拿到「樹枝」的兩個端點？

  • 那dfs的重點呢？在于處理節點本身？不關注其他？（豆包回答我）

層序遍歷：

// 輸入一棵二叉樹的根節點，層序遍歷這棵二叉樹
int levelTraverse(TreeNode* root) {if (root == nullptr) return;queue<TreeNode*> q;q.push(root);int depth = 0;// 從上到下遍歷二叉樹的每一層while (!q.empty()) {int sz = q.size();// 從左到右遍歷每一層的每個節點for (int i = 0; i < sz; i++) {TreeNode* cur = q.front();q.pop();// 將下一層節點放入隊列if (cur->left != nullptr) {q.push(cur->left);}if (cur->right != nullptr) {q.push(cur->right);}}depth++;}return depth;
}
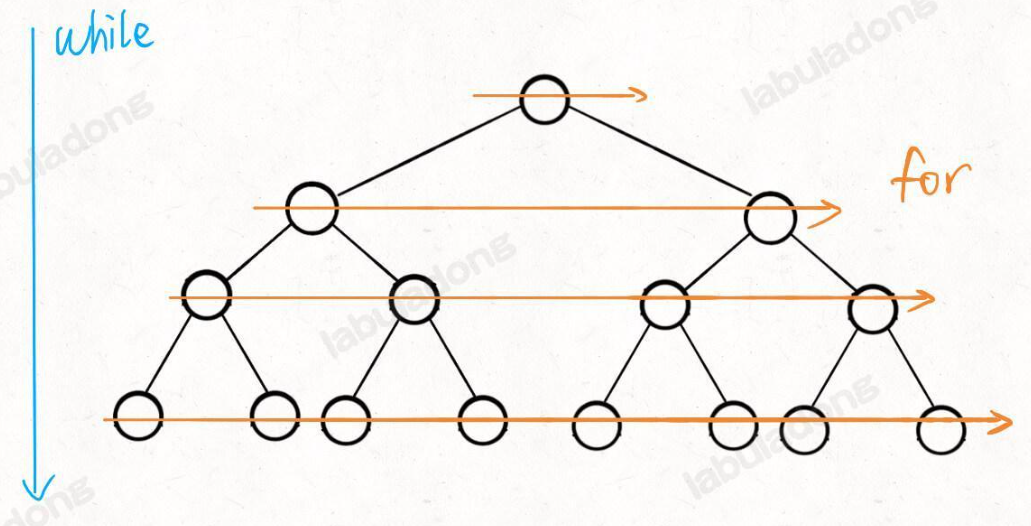
  • while循環和for循環分管從上到下和從左到右的遍歷！合力完成了層序遍歷！
    在這里插入圖片描述

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/914999.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/914999.shtml
英文地址，請注明出處：http://en.pswp.cn/news/914999.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

如何區分Bug是前端問題還是后端問題？

如何區分Bug是前端問題還是后端問題？

在軟件測試中，精準定位Bug的歸屬（前端 or 后端）是高效協作的關鍵。以下是系統化的排查方法，結合技術細節和實戰技巧： 1. 核心判斷邏輯 「數據 vs 展示」二分法： 后端問題：數據本身錯誤（API返回錯誤數據/邏輯錯誤/數據庫問題） 前端問題：數據正確但展示異常（UI渲染錯…
閱讀更多...
深入解析操作系統中的文件控制塊（FCB）：從原理到現代實現演進

深入解析操作系統中的文件控制塊（FCB）：從原理到現代實現演進

一、FCB的核心概念與基礎結構文件控制塊&#xff08;File Control Block, FCB&#xff09;是操作系統管理文件的核心元數據結構&#xff0c;充當文件系統與物理存儲間的橋梁。FCB本質上是文件在內存中的映射&#xff0c;包含文件的所有管理信息。傳統FCB通常占據32-44字節空間&…
閱讀更多...
python原生處理properties文件

python原生處理properties文件

這個工具類使用 Python 的 configparser 模塊操作 .properties 文件&#xff0c;核心是將 .properties 格式適配為 configparser 支持的 .ini 格式。 核心代碼解釋 1. 類初始化與配置解析 class Properties:def __init__(self, file_path: str, encoding: str utf-8):self.fil…
閱讀更多...
【java 安全】 IO流

【java 安全】 IO流

前言 IO是指 Input/Output&#xff0c;即輸入和輸出。以內存為中心&#xff1a; Input指從外部讀入數據到內存&#xff0c;例如把文件從磁盤讀取到內存&#xff0c;從網絡讀取數據到內存等等。Output指把數據從內存輸出到外部&#xff0c;例如把數據從內存寫入到文件&#xff0…
閱讀更多...
音視頻同步技術初剖析：原理、實現與FFmpeg分析

音視頻同步技術初剖析：原理、實現與FFmpeg分析

音視頻同步的基本原理 音視頻同步主要依靠以下幾個關鍵點&#xff1a;時間戳機制&#xff1a; 在封裝格式(如MP4)中&#xff0c;音頻幀和視頻幀都帶有時間戳(PTS, Presentation Time Stamp)這些時間戳表示該幀應該在什么時間被呈現同步策略&#xff1a; 音頻為主時鐘&#xff1…
閱讀更多...
掌控網頁的魔法之書：JavaScript DOM的奇幻之旅

掌控網頁的魔法之書：JavaScript DOM的奇幻之旅

掌控網頁的魔法之書&#xff1a;JavaScript DOM的奇幻之旅 在網頁開發的世界里&#xff0c;JavaScript就像一位魔法師&#xff0c;而DOM&#xff08;文檔對象模型&#xff09;則是它的魔法之書。沒有DOM&#xff0c;JavaScript就像失去了咒語的巫師&#xff0c;無法操控網頁的元…
閱讀更多...
【C語言】深入理解柔性數組：特點、使用與優勢分析

【C語言】深入理解柔性數組：特點、使用與優勢分析

C語言學習 柔性數組 友情鏈接&#xff1a;C語言專欄 文章目錄C語言學習前言&#xff1a;柔性數組一、柔性數組的特點二、柔性數組的使用三、柔性數組的優勢總結附錄上文鏈接專欄前言&#xff1a; 在有結構體和動態內存分配的知識后&#xff0c;今天咱們來說說柔性數組吧&…
閱讀更多...
RV126平臺NFS網絡啟動終極復盤報告

RV126平臺NFS網絡啟動終極復盤報告

1. 初始目標與環境目標: 將RV1126開發板的啟動方式&#xff0c;由從eMMC內部存儲掛載根文件系統&#xff08;rootfs&#xff09;&#xff0c;切換為通過網絡掛載位于NFS服務器上的根文件系統。動機: 提升開發調試效率&#xff0c;實現代碼修改后僅需重啟即可驗證&#xff0c;免…
閱讀更多...
一臺顯示器上如何快速切換兩臺電腦主機？

一臺顯示器上如何快速切換兩臺電腦主機？

我注意到很多人會遇到一個常見的情況&#xff1a;他們有兩臺電腦&#xff0c;一臺舊的用來處理基本的辦公任務&#xff0c;另一臺新的用來玩游戲。新手通常會用 DP端口連接第一臺電腦的顯示器&#xff0c;用 HDMI 連接第二臺電腦。當他們想在兩臺電腦之間切換時&#xff0c;經常…
閱讀更多...
抗輻照與國產替代：ASM1042在衛星光纖放大器(EDFA)中的應用探索

抗輻照與國產替代：ASM1042在衛星光纖放大器(EDFA)中的應用探索

摘要&#xff1a;本文以國科安芯推出的ASM1042芯片為例&#xff0c;通過分析ASM1042的抗輻照性能、高速數據傳輸能力、可靠性以及國產化優勢&#xff0c;結合EDFA系統的需求特點&#xff0c;深入探討了其在商業衛星光纖放大器&#xff08;EDFA&#xff09;項目中的應用潛力。AS…
閱讀更多...
鴻蒙ArkUI：聲明式開發，高效構建全場景體驗

鴻蒙ArkUI：聲明式開發，高效構建全場景體驗

目錄 導言&#xff1a;開啟鴻蒙應用開發的新范式 ArkUI框架概覽 - 鴻蒙UI的靈魂 深入核心 - 聲明式UI開發范式 命令式 vs 聲明式&#xff1a;范式革命 ArkUI如何實現聲明式&#xff1f; 創建內置組件 創建自定義組件 自定義組件的基本結構 ArkUI框架的核心特性與優勢 …
閱讀更多...
數據查找 二叉查找樹

數據查找 二叉查找樹

查找一般分為有序查找和無序查找&#xff0c;這邊在講有序查找例二分查找二分查找就是在有序數組中&#xff0c;通過mid(lowhigh)/2來判定中間值&#xff0c;將中間值與待查找的值進行比較&#xff0c;如果待查找的值大于中間值&#xff0c;那么就將范圍縮小&#xff0c;查找右…
閱讀更多...
幾款開源的安全監控與防御工具分享

幾款開源的安全監控與防御工具分享

安全監控與防御工具概述 在現代網絡安全架構中，合理選擇和部署一系列的安全監控、檢測、響應工具至關重要。下面我們將介紹一些常見的安全工具，包括 Elkeid、Wazuh、Caldera、ELK、Snort、Suricata、OpenHFW、OSSEC、GScan 和 Sysom，并詳細介紹它們的下載鏈接、用處、使用方…
閱讀更多...
Elasticsearch：ES|QL 改進的時間線

Elasticsearch：ES|QL 改進的時間線

作者&#xff1a;來自 Elastic Toms Mura 讓我們回顧一下 ES|QL 的歷史和它的改進。 更多閱讀&#xff0c;Elasticsearch&#xff1a;ES|QL 查詢展示。 Elasticsearch 配備了眾多新功能&#xff0c;幫助你為自己的用例構建最佳搜索方案。查看我們的示例筆記本了解更多內容&…
閱讀更多...
Linux | Bash 子字符串提取

Linux | Bash 子字符串提取

注&#xff1a;本文為 “ Bash 子字符串提取” 相關合輯。 英文引文&#xff0c;機翻未校。 如有內容異常&#xff0c;請看原文。 How to Extract Bash Substring? [5 methods] 如何提取 Bash 子字符串&#xff1f;[5 種方法] 2024-04-28 00:00:00 In Bash, a substring is…
閱讀更多...
Vue2 前端開發 - vue-quill-editor 富文本編輯器（編輯器基礎案例、編輯器配置參數解讀、編輯器事件）

Vue2 前端開發 - vue-quill-editor 富文本編輯器（編輯器基礎案例、編輯器配置參數解讀、編輯器事件）

一、vue-quill-editor 1、vue-quill-editor 概述vue-quill-editor 是一個基于 Quill 富文本編輯器的 Vue 組件vue-quill-editor 在 Vue 2 項目中可以很方便地集成與使用2、vue-quill-editor 安裝 執行如下指令&#xff0c;安裝 vue-quill-editor npm install vue-quill-editor …
閱讀更多...
斷網情況下，網線直連 Windows 筆記本 和Ubuntu 服務器

斷網情況下，網線直連 Windows 筆記本 和Ubuntu 服務器

在斷網情況下&#xff0c;通過網線直連 Windows 筆記本 和 Ubuntu 服務器&#xff0c;并使用 VSCode 訪問服務器及 Docker 容器 的步驟如下&#xff1a;1. 物理連接&#xff08;網線直連&#xff09; 1.1 使用網線連接 用 網線&#xff08;Cat5e 或更高&#xff09; 連接 Windo…
閱讀更多...
消息隊列總結

消息隊列總結

為什么需要消息隊列&#xff1f; 隨著互聯網快速發展&#xff0c;業務規模不斷擴張&#xff0c;技術架構從單體演進到微服務&#xff0c;服務間調用復雜、流量激增。為了解耦服務、合理利用資源、緩沖流量高峰&#xff0c;「消息隊列」應運而生&#xff0c;常用于異步處理、服務…
閱讀更多...
C#引用轉換核心原理：類型視角切換

C#引用轉換核心原理：類型視角切換

&#x1f50d; C#引用轉換核心原理&#xff1a;類型視角切換 引用類型由內存指針和類型標記組成&#xff08;如圖1&#xff09;。引用轉換不改變內存地址&#xff0c;僅改變編譯器識別對象的“視角”&#xff1a; B myVar1 new B(); // 實際B類型對象 A myVar2 (A)myV…
閱讀更多...
重要發布丨MaxKB V2正式發布，助力用戶快速構建企業級智能體

重要發布丨MaxKB V2正式發布，助力用戶快速構建企業級智能體

2025年7月18日&#xff0c;MaxKB V2版本正式發布。MaxKB是一個強大易用的企業級智能體平臺&#xff0c;致力于解決企業AI落地所面臨的技術門檻高、部署成本高、迭代周期長等問題&#xff0c;讓企業用戶落地AI更簡單。 秉承“開箱即用&#xff0c;伴隨成長”的設計理念&#xff…
閱讀更多...
最新文章

Copyright @ 2022~2023