SOTA方法

3D表示：格網和點
連續場景表示：
NeRF(體積射線行進優化多層感知機（MLP），以實現捕獲場景的新視圖合成)
插值存儲在體素、哈希網格或點中的值來構建連續表示
未考慮插值會受到外部噪聲干擾

3DGS contribution

1. 3D 高斯作為靈活且富有表現力的場景表示。
2. 使用 SfM 過程中生成的稀疏點云初始化 3D 高斯，僅使用 SfM 點作為輸入即可獲得高質量結。
3. 3D 高斯是可微的體積表示，同時可以通過投影到 2D 并應用標準 α 混合來非常高效地進行光柵化。
4. 3D 高斯屬性的優化 ——3D 位置、透明度 α、各向異性協方差和球面諧波（SH）系數
5. 3DGS屬性優化與自適應密度控制步驟交錯進行，在優化過程中添加和偶爾移除 3D 高斯。優化過程產生了場景的合理緊湊、非結構化且精確的表示
6. 快速可見性感知渲染：其使用快速 GPU 排序算法并受基于瓦片的光柵化啟發。然而，由于我們的 3D 高斯表示，我們可以執行尊重可見性順序的各向異性 splatting—— 借助排序和 α 混合 —— 并通過跟蹤所需數量的已排序 splat 的遍歷實現快速準確的反向傳播
   ??如何理解3DGS與自適應密度控制交錯進行？如何理解在優化過程添加和移除3DGS？如何理解快速GPU排序算法以及瓦片光柵化和各向異性splatting?什么是α混合？作用是什么？如何理解后向傳播？關注什么參數調整

傳統重建

基于點的渲染

NeRF

基礎知識補盲

光柵化

什么是光柵化？光柵化具體的實現步驟？

SFM

如何通過運動恢復結構（SfM）校準的相機

三角化

極線幾何

極平面、極線
在第二張圖像上面搜索空間點M在第一張圖像的投影點m的對應點m’的時候，只需要在對應的極線上搜索就可以了

標準的雙目立體視覺

條件
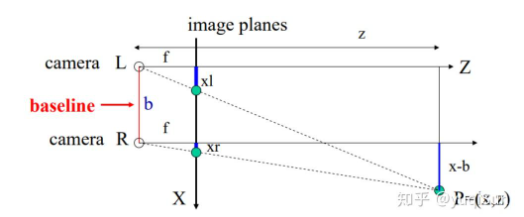
視差 d：指同一物體在左右兩張圖像中對應點的水平坐標差，在左視圖的列坐標x_l減去在右視圖上的列坐標x_r，是像素單位,則最終的水平視差為：d = x_l - x_r
深度
深度D等于像素在該視圖相機坐標系下Z坐標，是空間單位
視差圖
視差圖指存儲立體校正后單視圖所有像素視差值的二維圖像。

1. 視差圖是一張二維圖像，和原圖等大小
2. 視差圖每個位置保存的以像素為單位的該位置像素的視差值
3. 左視圖視差圖：在像素位置p的視差值等于該像素在右圖上的匹配點的列坐標減去其在左圖上的列坐標
   視差與深度的關系：視差與深度成反比：d = f x b / z對應的視差d越小，深度z越大(距離相機越遠)
4. 相機的視線平行
5. 相機光心連接構成的基線，與兩個相機的光軸平行
   極線校正——使兩幅圖像的極線相互平行

立體匹配理論與方法

主要用來估計圖像中每個像素點的可靠的深度信息
立體匹配理論：立體匹配的目的就是對同一三維場景的兩幅成像平面中的每一個像素點找到與其相匹配的點，于是可以計算出每個坐標點的視差值 d ，進而可以準確的描述場景的三維空間信息。
視差和深度之間的關系
立體匹配(視差估計)
輸入為一對在同一個時刻捕獲的經過極線校正的左右兩幅圖像I_r,I_l,輸出是由參考圖像中(左圖)中每個像素對應的視差值所構成的視差圖d。視差是三維場景中某一點在左右圖像中對應點位置的像素級差距。

立體匹配難點：
光照變化、遮擋、無紋理區域、重復紋理、視差不連續

立體匹配的基本流程

匹配代價計算：
衡量待匹配像素與候選像素之間的相關性。代價越小則說明相關性越大，是同名點的概率也越大。(是否為同名點都可以進行匹配計算)
每個像素在搜索同名點之前，往往會指定一個視差搜索范圍D（Dmin ~ Dmax）,視差搜索時將范圍限定在D內，用一個大小為W×H×D（W為影像寬度，H為影像高度）的三維矩陣C來存儲每個像素在視差范圍內每個視差下的匹配代價值。矩陣C通常稱為DSI（Disparity Space Image）。
選擇合適的匹配代價計算函數是立體匹配中不可忽視的關鍵步驟
代價聚合：

視差計算
視差優化

李群和李代數

這里首先利用了旋轉矩陣的正交性質，并考慮旋轉矩陣是具有連續時間變化的性質，對旋轉矩陣基于時間t求導
最終求導整理得出反對稱矩陣的性質

反對稱矩陣能夠用一個三維向量表示量 ?(t) ∈ R³——這也是反對稱矩陣與三維向量存在的性質
考慮在原點附近進行一階泰勒展開，同時考慮李群在原點附近的正切空間的性質，最終得到R(t)

特殊正交群SO₃與特殊歐式群SE₃
SO₃代表旋轉矩陣，而SE₃代表變換矩陣。
這里需要注意：SO₃旋轉矩陣具有約束條件，而且旋轉矩陣以及變換矩陣對加法不封閉，但是這些矩陣對乘法是封閉的

同時李群指的是具有連續(光滑)性質的群——SE(3)與SO(3)在實數空間上是連續的
李代數：
這里需要注意的是：李代數是一個由三維向量組成的集合，每個向量對應到一個反對稱矩陣，可以用于表達旋轉矩陣的導數
李群與李代數的關系為：**指數映射關系R = exp(?^{^}). **

對于羅德里格斯公式可以形象的理解為：旋轉矩陣R能夠通過利用模長θ以及單位方向向量a^{^}計算得出的，這樣可以將李代數so(3)中的任意一個三維旋轉向量，通過羅德里格斯公式，最終計算得出與指數映射等價的旋轉矩陣

姿態矩陣SE(3)上的指數映射：
首先：對于矩陣SE(3)，考慮為：
將矩陣SE(3)通過se(3)李代數通過指數映射表示為：

那么如何理解李代數呢？se(3)位于R⁶空間中，對應的SE(3)的李代數se(3)包含三維平移向量ρ以及三維旋轉向量φ

構建se(3)上面的指數映射：

得出se(3)的指數映射形式為：

將右上角的進行推導得：

平移部分經過指數映射后，發生了一次以J為系數矩陣的線性變換
那么怎么通過對數映射構建李群和李代數的關系呢？

1. 旋轉矩陣由9個量構成，但是一次旋轉只是存在3個自由度。
2. 旋轉矩陣自身帶有的約束：必須是正交矩陣，而且行列式為1
   通過一種方式，緊湊的描述旋轉和平移：
   旋轉矩陣R可以用一個單位長度的向量n，以及旋轉角度θ來描述這個變換
   羅德里格斯公式能夠明確這種變換
   注意Rn = n表示旋轉軸上的向量在旋轉后不發生任何變換，說明轉軸 n 是矩陣 R 特征值 1 對應的特征向量，并且“旋轉軸經過旋轉之后不變”
   
   李群與李代數的關系
   理解一下從SE(3)到se(3)的變化：
   通過能夠計算出旋轉角θ，然后李代數又可以表示為一個繞著某個固定軸a旋轉了θ角度的向量，也就是ε = θa，而繞著旋轉軸a旋轉角度θ，旋轉軸經過旋轉后仍然不變(Ra = a)，如果通過姿態矩陣T求得t的話，就很簡單！！！t = Jρ，而J可以通過θ和a求得，ρ就能夠簡單得出。
   
   大家可能會想：這個雅可比矩陣J怎么求——通過se(3)的羅德里格斯公式求解：
   

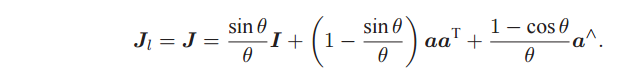
李群和李代數的映射

指數映射以及對數映射

李代數的求導

設計優化問題：

而針對于觀測到的每一個路標點，都會產生一個error誤差模型——最終的問題：尋找一個最優的T，使得整體誤差的參茶值最小：

這里觀察到：求解此問題，需要計算目標函數 J 關于變換矩陣 T 的導數。這里的重點是，我們經常會構建與位姿有關的函數，然后討論該函數關于位姿的導數，以調整當前的估計值。然而，SO(3), SE(3) 上并沒有良好定義的加法，它們只是群。如果我們把 T 當成一個普通矩陣來處理優化，那就必須對它加以約束(正交矩陣T*T^T = I,det(T) = 1)。而從李代數角度來說，由于李代數由向量組成，具有良好的加法運算。
!!! 使用李代數解決求導問題：

1. 用李代數表示姿態，然后根據李代數加法來對李代數求導
2. 對李群左乘或右乘微小擾動，然后對該擾動求導，稱為左擾動和右擾動模型。

李代數解決求導問題

BCH公式

上式對于φ₁，φ₂標量，該式成立。
但是將李代數通過指數映射轉化為矩陣形式——>ln (exp (A) exp (B)) = A + B
這里需要關注的問題：如果標量φ₁，φ₂成立，那么此時變成矩陣上式仍然滿足么？φ₁，φ₂的反對稱矩陣為矩陣的形式，所以如果φ₁ = A，φ₂ = B，那么整個式子變成如下形式，對于矩陣來說，為非標量，所以，上面的式子就不成立
兩個李代數指數映射乘積的完整形式，由 Baker-Campbell Hausdorff 公式（BCH 公式）給出

BCH 公式告訴我們，當處理兩個矩陣指數之積時，它們會產生一些由李括號組成的余項。但是SO(3) 上的李代數
ln (exp (?¹) exp (?²))∨，當 ?1 或 ?2 為小量時，小量二次以上的項都可以被忽略掉。
那么BCH 擁有線性近似表達：
== 這個公式將矩陣相乘轉化為李代數相加的形式做了等式的近似！！==

該式告訴我們，當對一個旋轉矩陣 R2（李代數為 ?²）左乘一個微小旋轉矩陣 R1（李代數為 ?¹）時，可以近似地看作，在原有的李代數 ?² 上加上了一項 J_l(?²)^?1?₁。
李代數在 BCH 近似下，分成了左乘近似和右乘近似兩種，在使用時我們須注意使用的是左乘模型還是右乘模型
這里的J對應的是羅德里格斯公式在姿態矩陣上成立的變形等式

！！！而右乘雅可比僅需要對自變量取負號


對應的李代數實現優化問題求導可以考慮為：

用李代數實現優化問題求導：
由于李代數由向量組成，具有良好的加法運算。因此，使用李代數解決求導問題的思路分為兩種：
1. 用李代數表示姿態，然后根據李代數加法來對李代數求導。
2. 對李群左乘或右乘微小擾動，然后對該擾動求導，稱為左擾動和右擾動模型。
第一種方式對應到李代數的求導模型，而第二種則對應到擾動模型。下面來討論這兩種思路的異同

李代數求導：

李代數的求導根據優化函數：

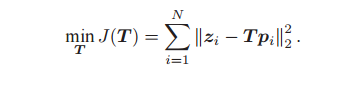
此時對于T矩陣進行求導，也就是對矩陣求導(將李代數Φ通過指數映射為R的形式)：

最終得到的函數對于R矩陣的求導為：

第 4 行至第 5 行將反對稱符號看作叉積，交換之后變號。們推導出了旋轉后的點相對于李代數的導數

利用李代數求導，引入了然含有形式比較復雜的 J_l，我們不太希望計算它

擾動模型則

由于這里仍然含有形式比較復雜的 J_l，我們不太希望計算它。而下面要講的擾動模型則提供了更簡單的導數計算方式。

！！！對于直接用李代數進行求導，通過對李代數先進性指數映射，然后進行左乘擾動，然后再通過對殘差函數求導，將對旋轉矩陣R的求導轉化為對李代數再經過左乘擾動模型后的求導
這里避免了計算直接對李代數求導后，引入了雅可比矩陣J_l，帶來額外的計算負擔，通過左乘擾動，能夠有效地規避J_l的計算
關注一下經過擾動模型得到的求導公式與直接對李代數求導的公式：
經過左乘擾動：

直接對李代數求導：

SE(3) 上的李代數求導

直接對姿態矩陣進行上面的左乘擾動，這樣能夠避免直接對李代數計算引入額外的雅可比矩陣J_l的復雜計算：



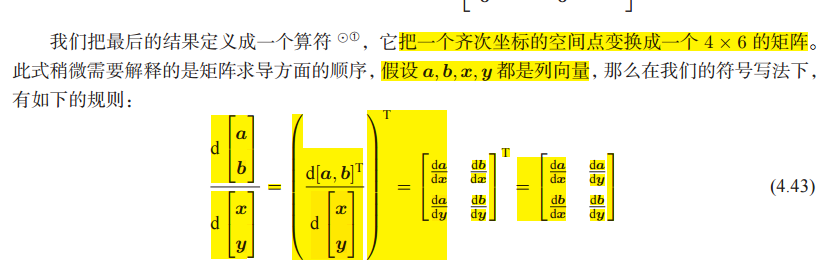
SE(3)上的推導：

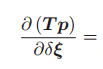
根據下面的求導規則：

得到如下計算結果：