1.多維特征

之前我們探討了單變量/特征的回歸模型，現在我們對房價模型增加更多的特征，例如房間數樓層等，構成一個含有多個變量的模型，模型中的特征為$（x1，x2，x\mathrm{3...}xn）$

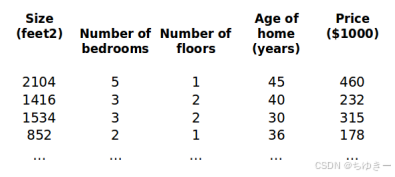
增添更多特征后，我們引入一系列新的注釋：
$n$代表特征的數量
$x^i$代表第 i 個訓練實例，是特征矩陣中的第i行，是一個向量（vector）。
$x_j^{\left(i\right)}$代表特征矩陣中第 i行的第j個特征，也就是第i個訓練實例的第 j個特征。
支持多變量的假設 ? 表示為： ?θ (x) = θ0 + θ1x1 + θ2x2 +. . . +θnxn
這個公式中有個n+1參數和個n變量，為了使得公式能夠簡化一些，引入x0=1 則公式轉化為：?θ (x) = θ0x0 + θ1x1 + θ2x2 +. . . +θnxn

此時模型中的參數是一個n + 1維的向量，任何一個訓練實例也都是n + 1維的向量公式可以簡化為：?θ(x) = θ?X其中上標T代表矩陣轉置。

2.多變量梯度下降

與單變量線性回歸類似，在多變量線性回歸中，我們也構建一個代價函數，則這個代價 函數是所有建模誤差的平方和，即：

$J({\theta }_0,{\theta }_1,\dots ,{\theta }_n)={\sum }_{i=1}^m(h_{\theta }(x^{(i)})?y^{(i)}{)}^2$

我們的目標和單變量線性回歸問題中一樣，是要找出使得代價函數最小的一系列參數。 多變量線性回歸的批量梯度下降算法為：

即：

求導得：

當n >= 1時，



我們開始隨機選擇一系列的參數值，計算所有的預測結果后，再給所有的參數一個新的值，如此循環直到收斂。

python代碼示例：

def computeCost(X, y, theta):inner = np.power(((X * theta.T) - y), 2) return np.sum(inner) / (2 * len(X))