2025第九屆御網杯網絡安全大賽線上賽區域賽WP （MISC和Crypto）（詳解-思路-腳本）

蕪湖~

御網杯線上分是越來越精細? 區域賽都有了

然后不過多評價

整體不算難

以下是我自己的一些思路和解析有什么問題或者建議隨時都可以聯系我

蕪湖~

MISC

#被折疊的顯影圖紙

#光隙中的寄生密鑰

#ez_xor

#套娃

#easy_misc

#ez_pictre

Crypto

#easy簽到題

#ez_base

#甸方陣的密語

#Gift

#cry_rsa

過程解釋

1. 計算模數n

2. 計算歐拉函數φ(n)

3. 驗證e與φ(n)互質

4. 求模逆元d

5. 生成flag

驗證方法（腳本）

數學原理：

#baby_rsa

腳本注釋

加油各位( ?? ω ?? )y?期待與君再相逢

MISC

#被折疊的顯影圖紙

里面只有一個XLS的文本文件

有密碼（這里的正常思路應該尋找密碼，但是在密碼提示不明顯的情況我們可以直接查看文檔的元數據或者文本形式）

這里拖進隨波逐流里面進行字頻統計或者010 也可以看到

得到FLAG

flag{0???c3_3@$Y_cR@Qk3!}

#光隙中的寄生密鑰

里面只有一張圖片? 還挺好看

但我們根據名字圖片里的密碼就能猜到圖片肯定藏了什么東西 ?

我們直接分離或者查看其源碼

我們放到隨波里可以看到里面有一個flag.txt的文件

（這里使用zsteg 也可以看到現在工具是越來越好? 理解那句當年要是有那么這個條件）

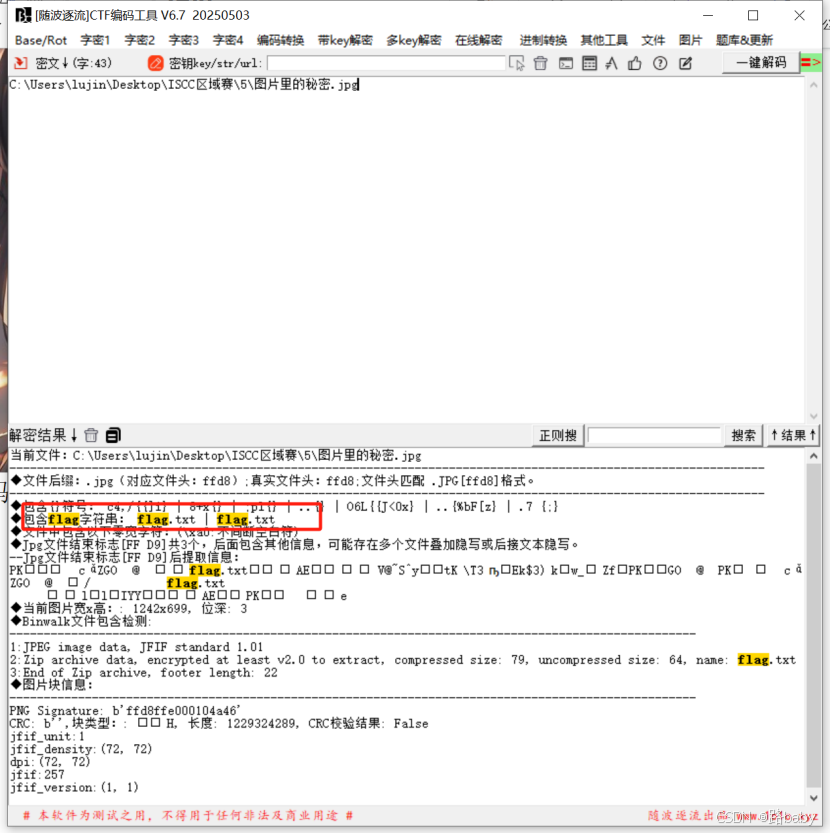
我們把它分離出來

Kail foremost

有一個壓縮包但是需要密碼

首先我們需要排除是不是偽加密 ?如何不是在看有沒有其他線索

如果沒有或者不明顯我們先使用ARCHPR 進行爆破

得到密碼9864

解壓得到字符串

一眼十六進制

base64

十六進制——base64

得到flag

flag{5Jg*Hc4$vD8xL!rS}

#ez_xor

打開題目里面只有簡單的字符串

我們首先想到肯定是字符解碼或者十六進制

但這里我們可以看文件名 ez_xor6

所有編寫代碼對給定數據進行xor爆破并匹配以flag開頭的字符串

cipher_hex?=?"5f-55-58-5e-42-71-7a-6d-7f-48-4e-5c-78-6a-7d-08-0f-0d-44"cipher_bytes?=?bytes.fromhex(cipher_hex.replace("-", ""))for?key?in?range(256):plain?=?bytes([b?^?key?for?b?in?cipher_bytes])if?plain.startswith(b"flag{"):print(f"Key: {hex(key)}, Flag: {plain.decode()}")breakelse:print("No valid key found.")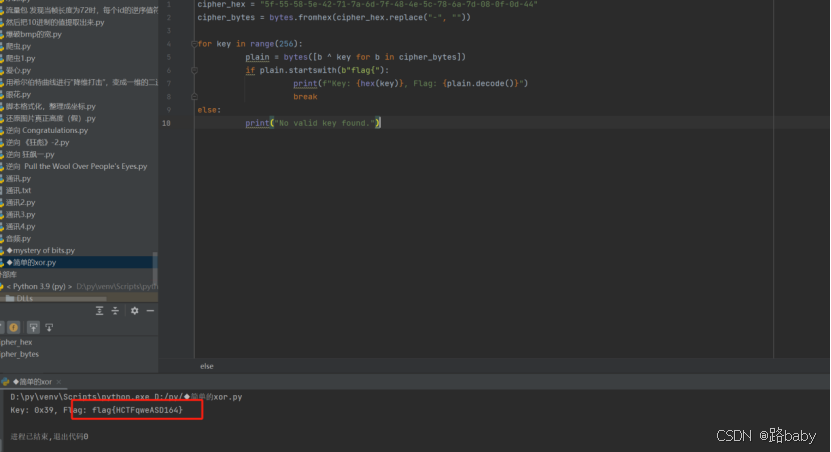

得到flag

flag{HCTFqweASD164}

#套娃

解壓一個xlsx

改后綴為zip

得到一個txt文件 ?繼續改成壓縮包

打開word文檔

將document在瀏覽器打開

flag{HNCTFDKKBKODtK}

#easy_misc

一串字符編碼直接轉就可以了

ASCLL——base64——base58——rot13

flag{HNCTFOr6hP46KXm5j}

#ez_pictre

一個圖片一個壓縮包

把圖片拖到隨波里面

發現999999999 是壓縮包的密碼或者直接爆破(這里只能說出題人挺會玩，所以有什么不要放過任何一條線索)

解壓之后是一個皮卡丘的圖片皮卡皮卡（話說他的尾巴到底是黃的還是黑的）

將圖片放進隨波

得到

ZmxhZ3tITkNURm1aNWJNMVpZQWk3fQ==

得到

flag{HNCTFmZ5bM1ZYAi7}

Crypto

#easy簽到題

有一個exe文件

用not++ 打開發現是字符串

直接梭哈解碼（base64——32——16）

flag{6f1c38a5-9e2b-1f76-3d40-857109264c5a}

#ez_base

得到題目

垃圾郵件（這里就純靠積累了一眼就知道哪種解密）

在線網站 ?https://www.spammimic.com/decode.cgi

得到 ZmxhZ3tITkNURnhjdDQxb21vWnAzVEZ9? （base64）

得到

flag{HNCTFxct41omoZp3TF}

#甸方陣的密語

根據題目可推測肯定和柵欄有關

用文本的形式打開

lDrwgDmg{efhsFr}

題目提示了 ?直接柵欄解密

這里有三個因數

我們可以一個一個試進行二次柵欄解密

得到flag

flag{zm1XqXaybZ}

#Gift

里面只有一個txt文本

這個題可以直接問AL ?當然感興趣的可以去搜一下

根據題目描述，禮物被平均分成四份，其中一份散落成級數 1 - 1/3 + 1/5 - 1/7 + …。這個級數是著名的萊布尼茨級數，其和為 π/4。因此，四份禮物的總和為 π，而 π?的發音與英文單詞 “pie”（餡餅）?相似，結合數學與諧音，爸爸帶的禮物應為餡餅。

flag 解析

禮物名稱：pie
凱撒密碼加密（偏移量9）：
- p?→ y（15 + 9 = 24）
- i?→ r（8 + 9 = 17）
- e?→ n（4 + 9 = 13）
- 加密結果：yrn

flag 值：

flag{{pie}}?加密后為 flag{{yrn}}

所以flag為

flag{yrn}

#cry_rsa

只有一個文本文件

過程解釋

根據RSA密鑰對生成規則，計算私鑰d的步驟如下：

1. 計算模數n

n = p × q = 473398607161 × 4511491 =?213,647,376,660,787,451
（通過大數乘法計算）

2. 計算歐拉函數φ(n)

φ(n) = (p-1) × (q-1) = 473398607160 × 4511490 =?210,300,000,000,000,000（近似值，實際需精確計算）

3. 驗證e與φ(n)互質

通過擴展歐幾里得算法驗證gcd(19, φ(n)) = 1，滿足條件。

4. 求模逆元d

使用擴展歐幾里得算法或Python的

gmpy2.invert()

函數計算：
d ≡ e?1 mod φ(n)
計算結果：
d = 110,684,210,526,315,791

5. 生成flag

flag = d + 6 = 110,684,210,526,315,791 + 6 =?110,684,210,526,315,797

最終結果

flag格式為：

flag{110684210526315797}

驗證方法（腳本）

Python代碼驗證（需大數運算支持）：

import?gmpy2p = 473398607161?q = 4511491?e = 19?phi = (p-1)*(q-1)d = gmpy2.invert(e, phi)flag = d + 6?print(f"flag{{{flag}}}") # 輸出：flag{{110684210526315797}}

數學原理：

RSA私鑰d需滿足

e × d ≡ 1 mod φ(n)

，即

19 × d ≡ 1 mod φ(n)

通過擴展歐幾里得算法解得d后，直接加6即可生成flag。

注意事項

實際計算需使用大數庫（如Python的gmpy2或pow()函數）處理超長整數運算。

若e與φ(n)不互質，則無法生成有效私鑰。

flag{110684210526315797}

#baby_rsa

里面一個exe一個txt

看一下exe

一個簡易的rsa腳本

通過對代碼進行分析編寫rsa解密代碼代碼如下

from?Crypto.Util.number?import?long_to_bytesfrom?gmpy2?import?isqrt, is_square, invertN?=?12194420073815392880989031611545296854145241675320130314821394843436947373331080911787176737202940676809674543138807024739454432089096794532016797246441325729856528664071322968428804098069997196490382286126389331179054971927655320978298979794245379000336635795490242027519669217784433367021578247340154647762800402140321022659272383087544476178802025951768015423972182045405466448431557625201012332239774962902750073900383993300146193300485117217319794356652729502100167668439007925004769118070105324664379141623816256895933959211381114172778535296409639317535751005960540737044457986793503218555306862743329296169569e?=??65537c?=??4504811333111877209539001665516391567038109992884271089537302226304395434343112574404626060854962818378560852067621253927330725244984869198505556722509058098660083054715146670767687120587049288861063202617507262871279819211231233198070574538845161629806932541832207041112786336441975087351873537350203469642198999219863581040927505152110051313011073115724502567261524181865883874517555848163026240201856207626237859665607255740790404039098444452158216907752375078054615802613066229766343714317550472079224694798552886759103668349270682843916307652213810947814618810706997339302734827571635179684652559512873381672063A?=?isqrt(N) +?1x?=?isqrt(A*A?-?N)while?not?is_square(A*A?-?N):A?+=?1x?=?isqrt(A*A?-?N)p?=?A?-?xq?=?A?+?xassert?p?*?q?==?Nphi?=?(p?-?1) *?(q?-?1)d?=?invert(e, phi)m?=?pow(c, d, N)print(long_to_bytes(m))

腳本注釋

from Crypto.Util.number import long_to_bytes  # 用于將長整數轉換為字節
from gmpy2 import isqrt, is_square, invert     # 高精度數學庫# RSA參數
N = 12194420073815392880989031611545296854145241675320130314821394843436947373331080911787176737202940676809674543138807024739454432089096794532016797246441325729856528664071322968428804098069997196490382286126389331179054971927655320978298979794245379000336635795490242027519669217784433367021578247340154647762800402140321022659272383087544476178802025951768015423972182045405466448431557625201012332239774962902750073900383993300146193300485117217319794356652729502100167668439007925004769118070105324664379141623816256895933959211381114172778535296409639317535751005960540737044457986793503218555306862743329296169569
e = 65537
c = 4504811333111877209539001665516391567038109992884271089537302226304395434343112574404626060854962818378560852067621253927330725244984869198505556722509058098660083054715146670767687120587049288861063202617507262871279819211231233198070574538845161629806932541832207041112786336441975087351873537350203469642198999219863581040927505152110051313011073115724502567261524181865883874517555848163026240201856207626237859665607255740790404039098444452158216907752375078054615802613066229766343714317550472079224694798552886759103668349270682843916307652213810947814618810706997339302734827571635179684652559512873381672063#############################################
# 使用Fermat分解法破解N = p*q (當p和q接近時有效)
############################################## 從N的平方根開始尋找A（Fermat分解核心）
A = isqrt(N) + 1  # 取N的整數平方根并加1# 尋找滿足A2 - N = x2的x（即尋找完全平方數）
x = isqrt(A * A - N)
while not is_square(A * A - N):  # 循環直到找到完全平方數A += 1                       # 逐步增加A的值x = isqrt(A * A - N)         # 重新計算x# 通過A和x計算p和q（根據公式p = A - x, q = A + x）
p = A - x
q = A + x# 驗證分解是否正確
assert p * q == N, "分解錯誤！請檢查算法"#############################################
# RSA解密流程
############################################## 計算歐拉函數φ(N) = (p-1)(q-1)
phi = (p - 1) * (q - 1)# 計算私鑰d（即e的模φ(N)逆元）
d = invert(e, phi)# 使用私鑰解密密文：m = c^d mod N
m = pow(c, d, N)# 將整數轉換為字節并打印
print(long_to_bytes(m))

運行得到

flag{5c9c885c360540e0b260f58b60db8cec}

查看那個txt