目錄

一、需求分析

1.1 問題描述

1.2 數據需求

1.3 功能需求

1.4 開發環境

二、概要設計

2.1 抽象數據類型 ADT 的定義

2.2 系統的主要功能模塊

2.3 功能模塊聯系圖

三、詳細設計

3.1 數據結構設計

3.2 主要算法

四、系統運行及結果分析

1. 用戶界面

2. 程序運行樣例

3. 程序結果分析

五、總結與思考

---

一、需求分析

1.1 問題描述

某工廠生產的產品需歷經 3 道工序，為提升效率，需確定加工順序，以實現生產 n 件產品的總時長最短。每件產品的各工序耗時各異。要求輸入 n（n≥10），并遞增 n 至少給出 3 組運行數據，對比程序運行時間。設計程序接收訂單信息及工序時長，據此計算最短生產時間，即完成所有產品所需的最小時間。程序核心任務是依據輸入優化工序安排，使總生產時間最小化。

1.2 數據需求

1. 輸入：訂單信息：接收產品數量 n，代表工廠要生產的產品總數。

1. 輸入：工序時長信息：以二維矩陣或數組呈現，行對應產品，列對應工序，元素表示相應工序的時長。

1.3 功能需求

1. 錯誤情況處理：輸入訂單及工序時長后，判斷輸入是否無效。若出現無效產品數量、負數工序時長等錯誤輸入，進行錯誤提示或異常處理。

1. 優化加工時長：運用分支限界法，根據輸入的產品數量及各產品工序耗時，計算生產 n 件產品的最小總時長。

1. 確定輸出：依據輸入，程序返回最小總時長，即完成 n 件產品所需的最短時間。

1. 確定最優加工順序：借助動態規劃算法結果，確定使總時長最小的工序順序。

1.4 開發環境

采用 Code::Blocks 作為開發環境，它是用于 C 和 C++ 等編程語言的集成開發環境（IDE），支持多種編譯器，具備強大調試功能，可在開發中定位代碼錯誤，還能將相關文件組織于項目中，便于代碼管理、版本控制與共享，提高開發效率。

二、概要設計

2.1 抽象數據類型 ADT 的定義

ADT 結構體

• • 數據對象：包含多種類型數據項，如變量、數組、指針等。

• • 數據關系：數據項間存在相關性。

• • 基本操作

• • • 創建：使用 typedef struct Node 創建新結構體對象。

• • • 訪問：通過結構體對象和成員名訪問成員。

• • • 賦值：將一個結構體對象賦值給當前對象。

• • • 修改：修改結構體中成員的值。

ADT info

• • 數據對象：信息記錄，含整型成員和數組成員。

• • 數據關系：無特定關系描述。

• • 基本操作：無特定操作描述。

ADT 線性表

• • 數據對象：相同數據類型數據元素的集合。

• • 數據關系：數據元素間有前驅后繼關系。

• • 基本操作

• • • 創建：構造空順序表 L。

• • • 插入：向線性表 L 中插入元素 e。

• • • 刪除：獲取并刪除線性表 L 的首個元素。

ADT 堆

• • 數據對象：包含元素實際數據及在堆中的位置信息。

• • 數據關系：對于非葉子節點 i，滿足 data [i] >= data [2 * i + 1] 和 data [i] >= data [2 * i + 2]（或 data [i] <= data [2 * i + 1] 和 data [i] <= data [2 * i + 2]）；對于節點 i 和 j，當 i 是 j 的祖先節點時，data [j] <= data [i]（或 data [j] >= data [i]）。

• • 初始條件：給定順序表 L，起始位置 s 和結束位置 m。

• • 操作結果：在給定范圍內對順序表 L 進行操作。

2.2 系統的主要功能模塊

1. inlIst 函數：初始化順序表 L 為空。
2. linsert 函數：向順序表 L 插入元素。
3. GetElem 函數：獲取并刪除順序表 L 的首個元素。
4. heaps 函數：實現堆排序中的堆調整操作。
5. Creat 函數：構建大根堆。
6. Sort 函數：對數組進行堆排序。
7. Min1 函數：計算指定節點 k 與其他節點權重的最小值。
8. Min2 函數：計算指定節點 k 與其他節點路徑權重之和的最小值。
9. fenzhi 函數：使用分支限界法求解最優路徑問題。
10. main 函數：程序入口，接收用戶輸入產品數量和加工時間，調用 fenzhi 函數求解最優路徑。
11. 異常處理模塊：判斷輸入是否無效，對無效輸入（如無效產品數量、負數工序時長）進行錯誤處理并給出提示。

2.3 功能模塊聯系圖

三、詳細設計

3.1 數據結構設計

1. 結構體

typedef struct {int x;int Lw[100] = {0};int M[100] = {0};int g;} info;

線性表

typedef struct {info data[MAXSIZE];int length;} Sqlist;

堆

void heaps(Sqlist &L, int s, int m) { //堆的創建int j;info rc;memcpy(&rc, &L.data[s], sizeof(info));for (j = 2 * s; j <= m; j = j * 2) {if (j < m && L.data[j].x < L.data[j + 1].x)++j;if (rc.x >= L.data[j].x)break;memcpy(&L.data[s], &L.data[j], sizeof(info));s = j;}memcpy(&L.data[s], &rc, sizeof(info));}void Creat(Sqlist &L) { //對堆進行創建和調整int n, i;n = (L.length);for (i = n / 2; i > 0; --i)heaps(L, i, n);}void Sort(Sqlist &L) { //是對 L 中的數據進行排序。int i;info X;Creat(L);for (i = L.length; i > 1; --i) {memcpy(&X, &L.data[1], sizeof(info));memcpy(&L.data[1], &L.data[i], sizeof(info));memcpy(&L.data[i], &X, sizeof(info));heaps(L, 1, i - 1);}}

3.2 主要算法

1. Min1 函數

int Min1(int k, int n, int M[100]) {int j, min = 10000;for (j = 1; j <= n; j++) {if (M[j] == 0 && j != k && min > f[j][3])min = f[j][3];}if (min == 10000)min = f[k][3];return min;}

該函數用于獲取未被處理且工序時間最短的產品的工序時間，輔助求解最優路徑。通過不斷調用可在決策節點選擇最優路徑。

2. Min2 函數

int Min2(int k, int n, info p) {int j;int db, sumf = 0;for (j = 1; j <= n; j++) {if (p.M[j] == 0)sumf = sumf + f[j][2];}db = (max(Sum(1, p.g + 1, k, p), Sum(2, p.g, k, p)) + sumf + Min1(k, n, p.M));return db;}

該函數用于計算當前節點的最小值，輔助求解最優路徑。通過不斷調用可在決策節點選擇最優路徑。

3. 分支限界法求解最優路徑

void fenzhi(int n, Sqlist &L) {info p, pl, e;int down = 10000, up = 100000;int i, j, x, db, sumf = 0, min3 = 100000;for (i = 1; i <= n; i++) {for (j = 1; j <= n; j++) {sumf = sumf + f[j][2];}for (j = 1; j <= n; j++) {if (j != i && min3 > f[j][3])min3 = f[j][3];}db = f[i][1] + sumf + min3;if (down > db) {down = db;x = i;}}e.x = down;e.M[x] = 1;e.Lw[1] = x;e.g = 1;linsert(L, e);while (L.length != 0) {p = GetElem(L);if (p.Lw[n] != 0) {e = GetElem(L);printf("所需最短時間是:%d\n路徑是: ", p.x);for (i = 1; i <= n; i++) {printf("%d ", p.Lw[i]);}} else {for (i = 1; i <= n; i++) {pl = p;if (p.M[i] == 0) {pl.Lw[p.g + 1] = i;pl.M[i] = 1;pl.g = p.g + 1;pl.x = Min2(i, n, p);if (pl.x < up) {linsert(L, pl);Sort(L);if (pl.g == n) {up = pl.x;deleted(down, up, L);}}}}}}}

該函數實現分支限界法算法框架，通過生成新路徑節點并選擇最優路徑，最終找到最優路徑，輸出最短時間和路徑。

四、系統運行及結果分析

1. 用戶界面

2. 程序運行樣例

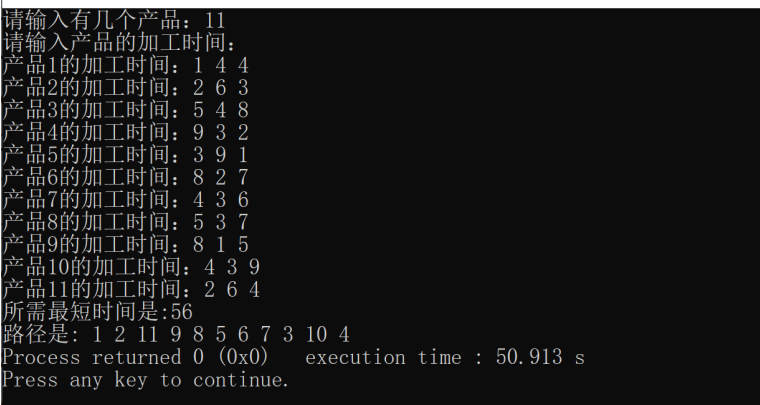
3. 程序結果分析

對比運行樣例輸出與手動計算結果，結果相似。同時記錄不同 n 值下程序的運行時間，分析隨著 n 增大，程序運行時間的變化趨勢。若運行時間增長過快，可能需進一步優化算法或數據結構。

五、總結與思考

完成此作業過程中，深入學習了分支限界法及其應用。分支限界法是求解最優化問題的常用算法，通過搜索和剪枝高效尋找最優解。在此問題中，定義數據結構和函數，利用分支限界法搜索解空間，剪去不必要路徑找到最優解。編寫代碼和運行程序過程中，深刻理解了分支限界法思想和實現。發現合理的排序和剪枝策略可大幅減少搜索空間、提高算法效率，且合理設計數據結構和算法能使代碼更清晰易理解。此外，認識到編程中錯誤處理和輸入驗證的重要性，添加對無效輸入的處理避免程序出錯。總之，通過解決此問題，掌握了分支限界法應用，加深了對算法設計和錯誤處理的認識，為今后學習和工作奠定了基礎。