


STL 中有哪些常見的容器
STL 中容器分為順序容器、關聯式容器、容器適配器三種類型,三種類型容器特性分別如下:
1. 順序容器 容器并非排序的,元素的插入位置同元素的值無關,包含 vector、deque、list?
- vector:動態數組 元素在內存連續存放。隨機存取任何元素都能在常數時間完成。在尾端增刪元素具有較佳的性能。
- deque:雙向隊列 元素在內存連續存放。隨機存取任何元素都能在常數時間完成(僅次于 vector )。在兩端增刪元素具有較佳的性能(大部分情況下是常數時間)。
- list:雙向鏈表 元素在內存不連續存放。在任何位置增刪元素都能在常數時間完成。不支持隨機存取。
2. 關聯式容器 元素是排序的;插入任何元素,都按相應的排序規則來確定其位置;在查找時具有非常好的性能;通常以平衡二叉樹的方式實現,包含set、map。
- set? set中不允許相同元素
- map map 與 set 的不同在于 map 中存放的元素有且僅有兩個成員變,一個名為 first,另一個名為 second,map 根據 first 值對元素從小到大排序,并可快速地根據 first 來檢索元素。
3. 容器適配器 封裝了一些基本的容器,使之具備了新的函數功能,包含 stack、queue。
- stack:棧 棧是項的有限序列,并滿足序列中被刪除、檢索和修改的項只能是最進插入序列的項(棧頂的項),后進先出。
- queue:隊列 插入只可以在尾部進行,刪除、檢索和修改只允許從頭部進行,先進先出。
STL 容器用過哪些,查找的時間復雜度是多少,為什么?
以下是其中一些常見容器的查找時間復雜度以及原因:
vector(向量):查找時間復雜度為O(n),因為vector是基于數組實現的,需要線性遍歷整個數組來查找元素。
deque(雙端隊列):在未排序狀態下,查找時間復雜度為O(n),類似于vector。但在有序狀態下,可以利用二分查找,降低查找時間復雜度為O(log n)。
list(鏈表):查找時間復雜度為O(n),因為鏈表是一種線性結構,需要從頭開始順序查找元素。
set(集合)和multiset(多重集合):查找時間復雜度為O(log n),底層通常使用紅黑樹實現,具有較好的平衡性能。
map(映射)和multimap(多重映射):查找時間復雜度為O(log n),底層通常使用紅黑樹實現,按鍵進行自動排序。
stack(棧)和queue(隊列):查找時間復雜度為O(n),因為它們是容器適配器,提供了先進先出(FIFO)或后進先出(LIFO)的接口,并不支持快速查找操作。
因此,對于不同的STL容器,其查找時間復雜度取決于底層數據結構的實現方式和算法設計。
vector 和 list 的區別,分別適用于什么場景?
vector 和 list 的區別:
底層數據結構:
- vector: 底層使用動態數組實現。
- list: 底層使用雙向鏈表實現。
插入和刪除操作:
- vector: 插入和刪除元素效率低。
- list: 插入和刪除元素效率高,因為只需要修改相鄰節點的指針。
隨機訪問:
- vector: 支持隨機訪問,可以通過下標快速訪問元素。
- list: 不支持隨機訪問,只能通過迭代器順序訪問元素。
空間和內存分配:
- vector: vector 一次性分配好內存,不夠時才進行擴容。
- list: list 每次插入新節點都會進行內存申請。
適用場景:
vector: 適用于連續存儲,支持隨機訪問,而不在乎插入和刪除的效率。
list: 適用于不連續的內存空間,如果需要高效的插入和刪除,而不關心隨機訪問。
簡述 vector 的實現原理
vector 是一種動態數組,在內存中具有連續的存儲空間,支持快速隨機訪問,由于具有連續的存儲空間,所以在插入和刪除操作方面,效率比較慢。
當 vector 的大小和容量相等(size==capacity)時,如果再向其添加元素,那么 vector 就需要擴容。vector 容器擴容的過程需要經歷以下 3 步:
- 重新在堆上創建更大的動態數組,大小是原來的2倍;
- 將舊內存空間中的數據,按原有順序移動到新的內存空間中;
- 最后將舊的內存空間釋放。
擴容以后它的內存地址會發生改變
迭代器失效原因,有哪些情況
迭代器失效是指迭代器在遍歷容器過程中,由于容器的結構發生改變而導致迭代器指向的元素不再有效。
以下是導致迭代器失效的常見情況:
- 插入和刪除操作: 當在容器中插入或刪除元素時,可能會導致容器內存重新分配或元素位置的改變,這可能會使迭代器失效。
- 清空容器: 清空容器會使容器內的所有元素被刪除,這樣迭代器指向的元素就會失效。
- 使用引起重新分配的操作: 例如,在
vector中使用push_back()添加元素時,如果超出了當前容量,可能會觸發重新分配操作,從而使所有迭代器失效。- 排序操作: 如果在排序過程中,容器的元素被移動了位置,迭代器可能會失效。
- 使用非常量迭代器遍歷過程中修改了容器: 如果在使用非常量迭代器遍歷容器的過程中,修改了容器的結構(例如插入或刪除元素),會使迭代器失效。
deque 的實現原理
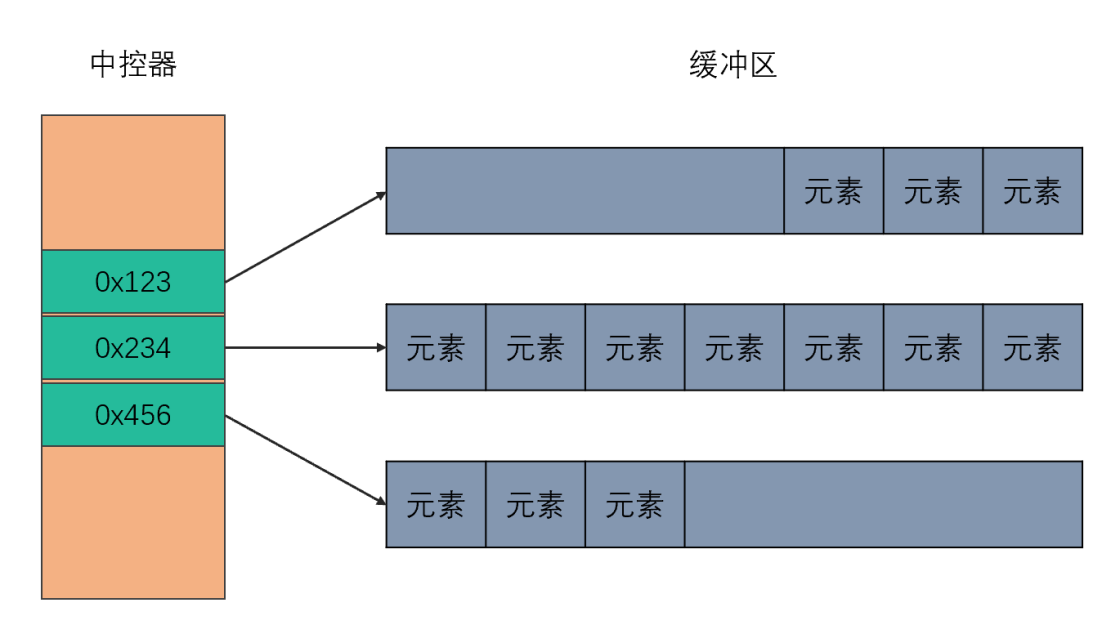
分段連續內存、中控器
deque 是由一段一段的連續空間構成。一旦有必要在 deque 前端或者尾端增加新的空間,便配置一段連續定量的空間,串接在 deque 的頭端或者尾端。
deque 采取一塊所謂的 map(不是 STL 的 map 容器)作為主控,這里所謂的 map 是一小塊連續的內存空間,其中的每個元素(此處成為一個結點)都是一個指針,指向另一段連續性內存空間,稱作緩沖區。緩沖區才是 deque的存儲空間的主體。
紅黑樹的特性,為什么要有紅黑樹
紅黑樹是一種自平衡的二叉搜索樹,它具有以下特性:
- 節點顏色: 每個節點要么是紅色,要么是黑色。
- 根節點和葉子節點: 根節點、葉子節點(NIL節點,即空節點)是黑色的
- 顏色相鄰節點規則: 不能有兩個相鄰的紅色節點。
- 從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。 這保證了紅黑樹的關鍵性質:最長路徑不超過最短路徑的兩倍。
2. 各操作的時間復雜度 插入: O(logN) 查看: O(logN) 刪除: O(logN)
map/Set 實現原理,各操作的時間復雜度是多少
1. map 實現原理 map 內部實現了一個紅黑樹,紅黑樹有自動排序的功能,因此 map 內部所有元素都是有序的,紅黑樹的每一個節點都代表著 map 的一個元素。因此,對于 map 進行的查找、刪除、添加等一系列的操作都相當于是對紅黑樹進行的操作。map 中的元素是按照二叉樹存儲的,特點就是左子樹上所有節點的鍵值都小于根節點的鍵值,右子樹所有節點的鍵值都大于根節點的鍵值,使用中序遍歷可將鍵值按照從小到大遍歷出來。
2. 各操作的時間復雜度 插入: O(logN) 查看: O(logN) 刪除: O(logN)
unordered_map 實現原理
unordered_map 容器和 map 容器一樣,以鍵值對(pair類型)的形式存儲數據,存儲的各個鍵值對的鍵互不相同且不允許被修改。但由于 unordered_map 容器底層采用的是哈希表存儲結構,該結構本身不具有對數據的排序功能,所以此容器內部不會自行對存儲的鍵值對進行排序。底層采用哈希表實現無序容器時,會將所有數據存儲到一整塊連續的內存空間中,并且當數據存儲位置發生沖突時,解決方法選用的是“鏈地址法”(又稱“開鏈法”).
map,unordered_map 的區別
- map是基于紅黑樹實現的,unordered_map是基于哈希表實現的
- map根據元素的鍵值會自動排序,而unordered_map是亂序的
- map的增刪改查時間復雜度是O(logN),而unordered_map的時間復雜度是最好情況是O(1),最壞情況是O(N)。






-基于RDKit描述符的分子從頭設計DOCK_D3N)








)
)

)
— 安裝運行Hello World)
