它只是一種手段，一種直觀而高效地表示復雜狀態的手段。

我們先來看一道比較基礎的：

直接DFS是肯定不行，我們發現對某一行，只要它前面放的位置都一樣，那么后面的結果也一樣。

因此我們考慮用DP，并且只有0/1，我們用二進制壓縮。

我們令f[i][st]表示前i行狀態為st的個數。

我們易得狀態轉移方程為：f[i][st]=(第i行放在第j列）

同時我們保證(st'&(1<<(j-1))==0&&st'+1<<(j-1)==st。

但是我們會遇到一個問題：怎么枚舉st?

其實，我們可以不用二維數組，從1二進制枚舉到1<<(n)-1，因為得到它的肯定比他小，肯定是計算過的，因此我們可以這么做，這里假設狀態為1101，那我們如何獲得1100,1001,0101呢？

用lowerbit操作，x&-x就得到了X中最低位的1及其后面的0，這樣子就ok了。

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,m,dp[1<<20],bu[25],x,y;
int lowerbit(int x){return (x&(-x));
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);bu[x]+=1<<(y-1);}int j,cnt;dp[0]=1;for(int i=1;i<=((1<<n)-1);i++){j=i;cnt=0;while(j!=0){j-=lowerbit(j);cnt++;}j=i;while(j!=0){int fk=lowerbit(j);if((fk&bu[cnt])==0){dp[i]+=dp[i^fk];}j-=fk;}}cout<<dp[(1<<n)-1];	
}

讓我們看看比較有意思的題吧：

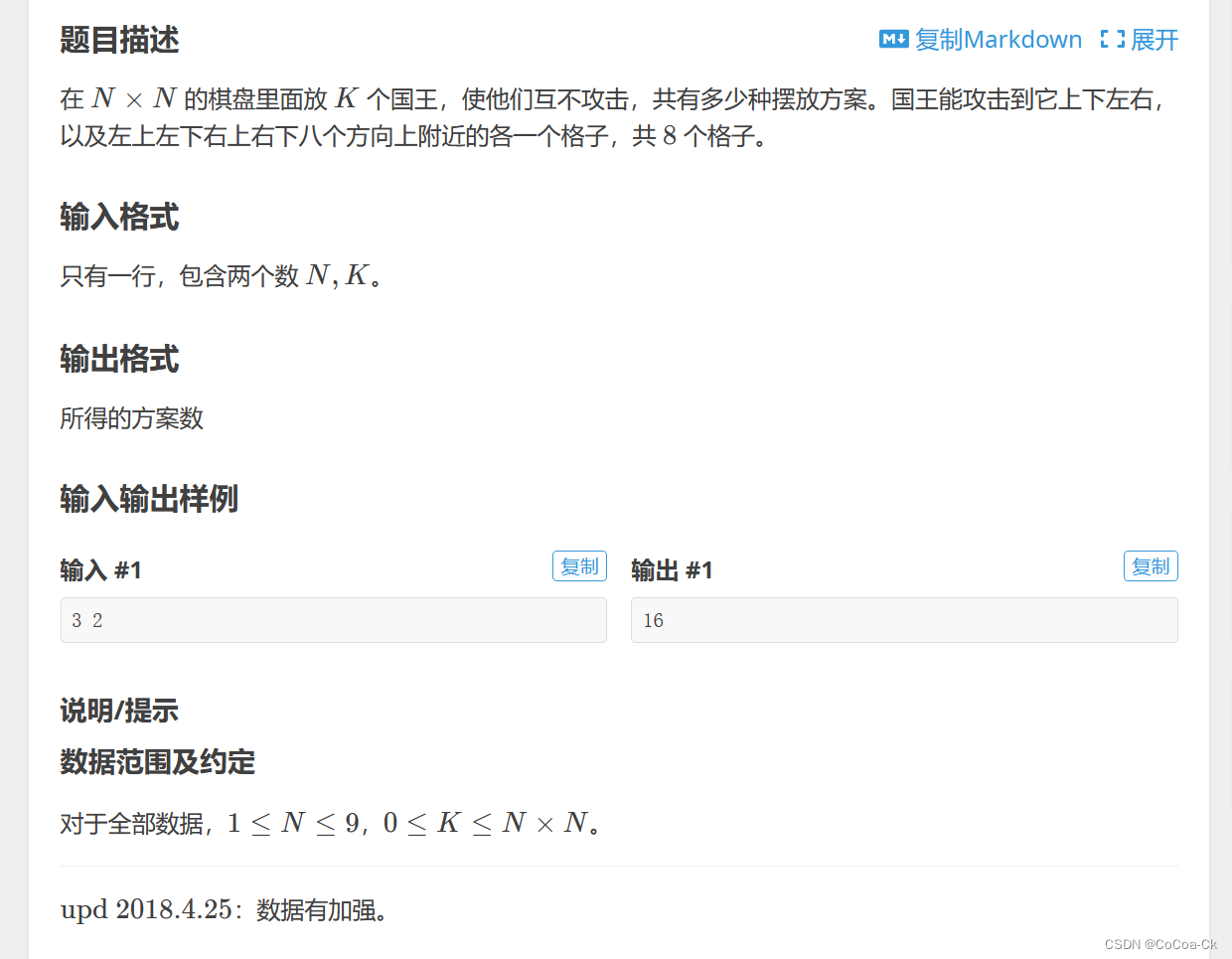
首先，如果我們一個一個看DFS的話，我們會發現第二個位置不像八皇后范圍很容易確認+81個格子，時間不允許，用一般的DP實現起來很麻煩，因為當我們要放一個國王時，我們還得知道能不能放，即不滿足無后效性。

于是我們可以換一種思路：

我們一行一行看，這樣子，當我們放當前行時，關注的只有上一行，而在這一行只要不相鄰即可。

我們令放了國王為1，沒放為0.

現在我們看是否合法：

1.同一行不相鄰：(x&(x<<1))==0(注意加括號）

2.如果上一行的狀態為x,當前為y，xy要滿足什么條件合法？

(x&y)==0 (x&(y<<1))==0 (x&(y>>1))==0

因此，我們令f[i][j][k]表示第i行，狀態為k時已經放了j個的方案數；

易得狀態轉移方程：

f[i][j][k]+=f[i-1][j-num(k)][p](k自己合法,p也合法,(k&p)==0 (k&(p<<1))==0 (k&(p>>1))==0)

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,k,num[1500];
long long dp[10][90][1000];
int calc(int num){int ans=0;while(num!=0){if((num&1)==1) ans++;num>>=1;}return ans;
}
int main(){cin>>n>>k;dp[0][0][0]=1;for(int i=0;i<(1<<n);i++){//打表num[i]=calc(i);}for(int i=1;i<=n;i++){for(int j=0;j<=k;j++){for(int st=0;st<(1<<n);st++){if((st&(st<<1))!=0) continue;if(num[st]>j) continue;for(int p=0;p<(1<<n);p++){if((p&(p<<1))!=0) continue;if((p&(st<<1))!=0) continue;if((p&(st>>1))!=0) continue;if((p&(st))!=0) continue;dp[i][j][st]+=dp[i-1][j-num[st]][p];}}}}long long ans=0;for(int st=0;st<(1<<n);st++){ans+=dp[n][k][st];}cout<<ans;
}