一、算法原理

表面法線是幾何表面的重要屬性，在許多領域（例如計算機圖形應用程序）中大量使用，以應用正確的光源來生成陰影和其他視覺效果。

給定一個幾何表面，通常很容易將表面上某個點的法線方向推斷為垂直于該點表面的向量。但是，由于我們獲取的點云數據集代表了真實表面上的一組點樣本，因此有兩種可能性：

• 從獲取的點云數據集中獲取底層表面，使用表面網格劃分技術，然后從網格計算表面法線；
• 使用近似值直接從點云數據集推斷表面法線。

1.理論入門

盡管存在許多不同的法線估計方法，但我們將在本教程中重點介紹的方法是最簡單的方法之一，其公式如下。確定表面上一點的法線的問題近似于估計與表面相切的平面的法線的問題，這反過來又變成了最小二乘平面擬合估計問題。

有關更多信息，包括最小二乘問題的數學方程，請參閱pclpy 最小二乘法擬合平面-CSDN博客。

因此，用于估計表面法線的解決方案簡化為對從查詢點的最近鄰居創建的協方差矩陣的特征向量和特征值（或 PCA – 主成分分析）進行分析。更具體地說，對于每個點pi，我們C按如下方式組裝協方差矩陣：

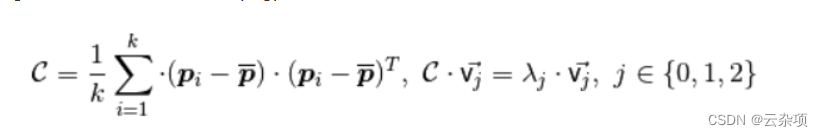
為考慮點鄰居的數目在附近 pi，p 表示3D質心最近的鄰居，入j是 j)協方差矩陣的特征值第，并且vj 在j個特征向量。

一般來說，因為沒有數學方法來求解法線的符號，如上所示通過主成分分析 (PCA) 計算的方向是不明確的，并且在整個點云數據集上的方向不一致。下圖展示了這些對代表廚房環境一部分的較大數據集的兩個部分的影響。圖的右半部分表示擴展高斯圖像 (EGI)，也稱為法線球體，它描述了點云中所有法線的方向。由于數據集是 2.5D，因此是從單個視點獲取的，因此法線應僅出現在 EGI 球體的一半上。然而，由于方向不一致，它們遍布整個球體。

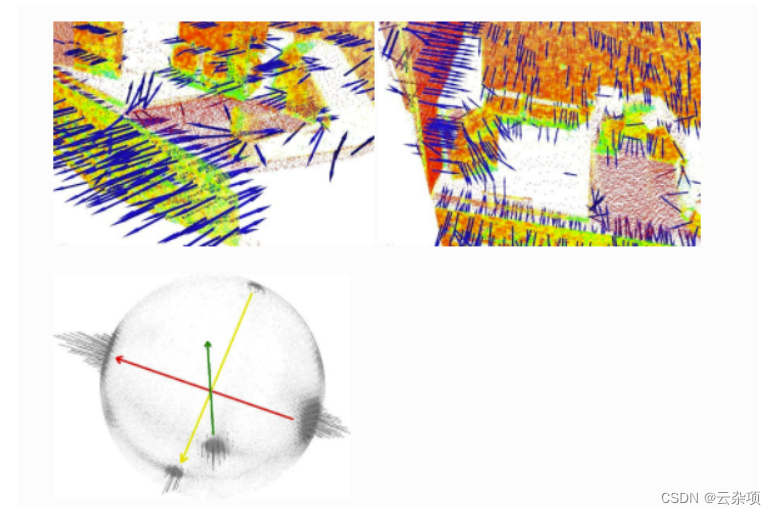
如果觀點vp 實際上是已知的，那么這個問題的解決方案是微不足道的。為了使所有法線ni 一致地朝向視點，它們需要滿足等式：

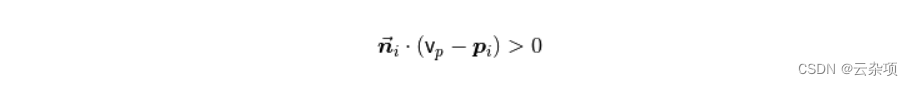
下圖顯示了上圖數據集中的所有法線一致指向視點后的結果。

2.選擇正確的比例

如前所述，一個點的表面法線需要從該點的周圍點鄰域支持（也稱為k-neighborhood）估計 。

最近鄰估計問題的細節提出了正確比例因子的問題：給定采樣點云數據集，正確的k（通過pcl::Feature::setKSearch給出）或r（通過pcl::Feature給出）是多少 ::setRadiusSearch ) 值應該用于確定一個點的最近鄰居集？

這個問題非常重要并且構成了點特征表示的自動估計（即，沒有用戶給定閾值）的限制因素。為了更好地說明這個問題，下圖展示了選擇較小尺度（即較小的r或k）與較大尺度（即較大的r或k ）的效果）。圖中的左側部分描繪了一個合理的精心選擇的比例因子，兩個平面的估計表面法線近似垂直，整個桌子上都可以看到小邊緣。然而，如果比例因子太大（右側部分），因此相鄰表面的鄰居集合更大，覆蓋來自相鄰表面的點，則估計的點特征表示會失真，在兩個平面的邊緣處具有旋轉的表面法線，并被涂抹邊緣和抑制細節。

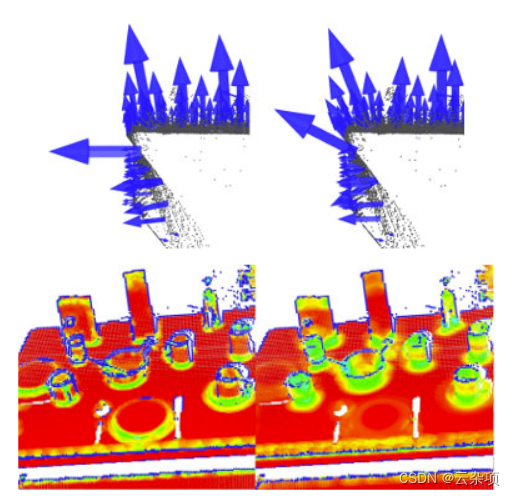
無需涉及太多細節，現在假設必須根據應用程序所需的詳細程度來選擇確定點鄰域的尺度就足夠了。簡而言之，如果杯子手柄和圓柱部分之間邊緣的曲率很重要，則比例因子需要足夠小以捕捉這些細節，否則就大。

二、代碼

from pclpy import pclif __name__ == '__main__':# 加載點云cloud = pcl.PointCloud.PointXYZ()reader = pcl.io.PCDReader()reader.read("res/bunny.pcd", cloud)print(cloud.size())  # 打印點云的數目# 構造法線估計類ne = pcl.features.NormalEstimation.PointXYZ_Normal()  # 法線對象ne.setInputCloud(cloud)  # 將cloud放入到ne中tree = pcl.search.KdTree.PointXYZ()  # 建立kd搜索樹ne.setSearchMethod(tree)cloud_normals = pcl.PointCloud.Normal() ne.setRadiusSearch(0.03)  # 設置半徑搜索領域0。03m# 計算法線ne.compute(cloud_normals)  # 計算法線print(cloud_normals.size())  # 打印法線的數目

三、結果

[output]
點云數目： 35947
法線數目： 35947

四、相關數據

法線估計官網：Normal Estimation Using Integral Images — Point Cloud Library 0.0 documentation (pcl.readthedocs.io)