線性規劃的用處非常的廣泛，這主要是因為很多類型的問題是可以通過轉化的方式轉化為線性規劃的問題。例如需要再圖論中尋找起始點到給定的點的最短路徑問題：

添加圖片注釋，不超過 140 字（可選）

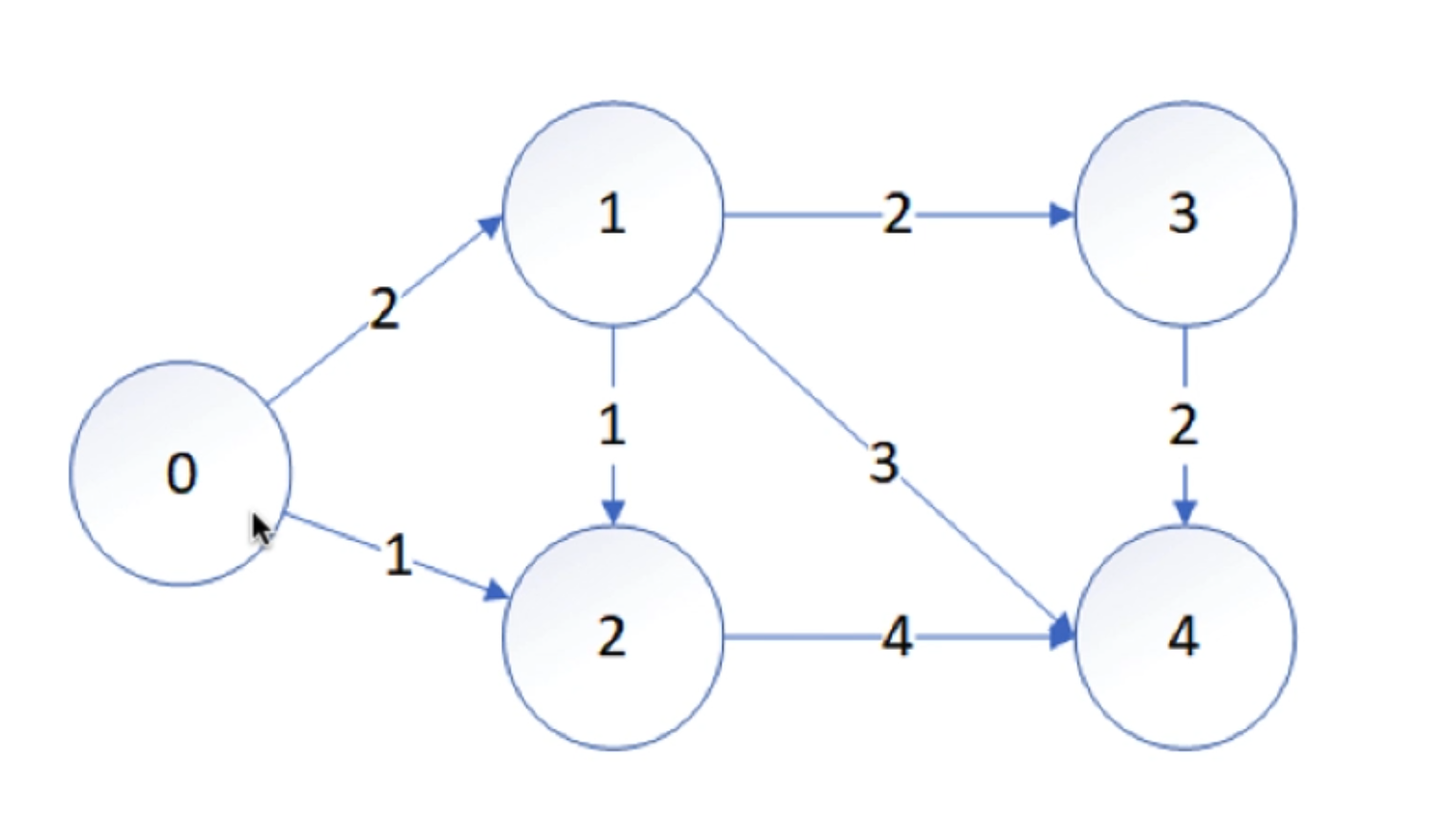
假設要計算從節點0到節點4的最短路徑，用變量d1到d4來表示節點0到節點1,2，3,4的最短路徑，那么解決這個問題的本質上是解決如下的一個線性規劃系統：

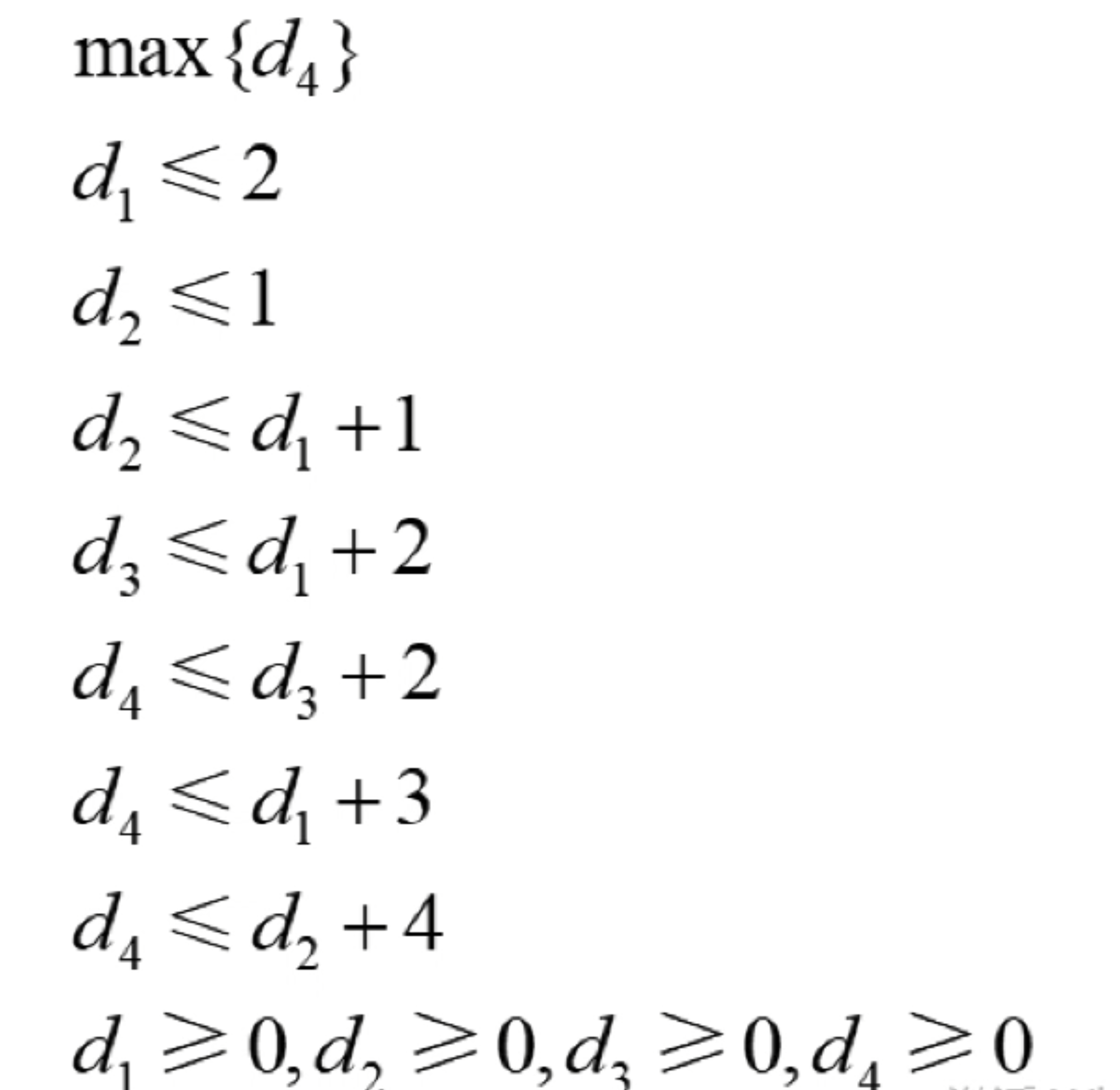
添加圖片注釋，不超過 140 字（可選）

而這里要注意的是問題所需要求的是最短路徑，按照目標函數應該是查找最小值才對，但是這里是查找的最大值，因為如果查找最小值，那么問題的答案就是將所有變量設置為0，而這就與所需要的目標是不相符的。

由于最短路徑肯定大于0，同時最短路徑一定能滿足上面線性系統的約束條件，且最大化可以讓我們找到一個非零解，因此它才能對應正確的最短路徑。

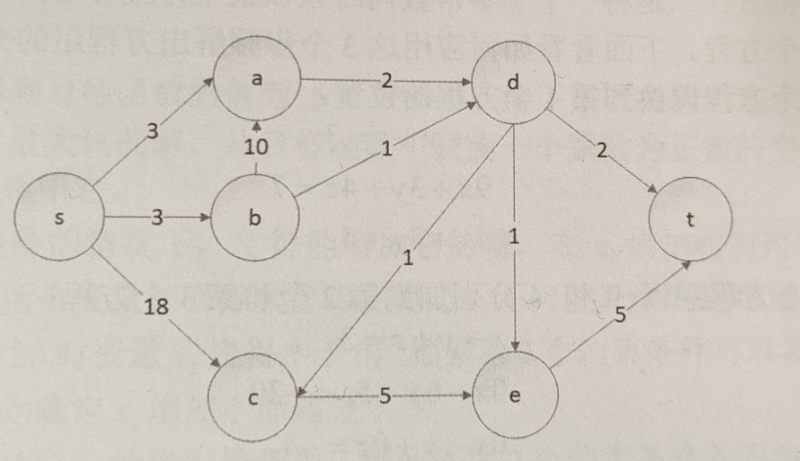
在圖論中還存在一種稱為極大流的問題，如果給定一個有向圖G，其中有一個起點和一個終點，在兩者之間存在很多中間點，同時點與點之間的連接存在一個容量上限，問題是從起點開始發出多少流量，這些流量分流到各個支路后，最終匯合到終點，試問起點能夠發出的流量最大是多少

添加圖片注釋，不超過 140 字（可選）

上圖中相互連接的節點其路徑上的數字表示能夠通過該路徑的最大流量，例如邊sa的值就是3，因此從節點s流向節點a的流量最大不能超過3，如果用c(u,v)來表示兩個連接節點間的最大容量，如c(s,a)=3，那么就有c(u,v)>0，同時用f(u,v)表示從s點出發的最大流量經過每一條管道時的流量，那么就可以制定出對應的線性規劃系統如下：

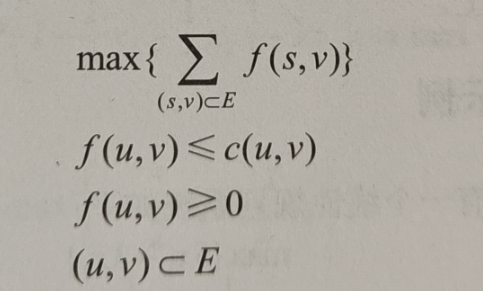
添加圖片注釋，不超過 140 字（可選）

這里的E表示所有邊的集合，所以有很多類型的問題是可以通過轉化成為線性規劃問題的。