梯度下降算法

在機器學習中，梯度下降算法常用于最小化代價函數（或損失函數），以此來優化模型的參數。代價函數衡量的是模型預測值與實際值之間的差異。通過最小化這個函數，我們可以找到模型預測最準確的參數。

代價函數

代價函數（Cost Function）或損失函數（Loss Function），是用來衡量模型預測值與真實值之間差異的一個函數。在回歸問題中，一個常見的代價函數是均方誤差

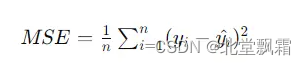
其中n是樣本數量，yi是樣本的真實值，被減去的則是預測值，這個值越小，說明預估越接近真實值。

實際案例：從簡單線性回歸理解梯度下降算法

假設我們有一組數據，表示房屋的大小與其價格的關系。我們想要構建一個簡單的線性回歸模型來預測房價，模型形式為
y=wx+b，其中 y 是房價，x 是房屋大小，w 是斜率，b 是截距。
第一步要做的是：初始化模型參數：隨機選擇w 和 b 的初始值，比如 w=0 和 b=0。計算代價函數的梯度：首先，我們需要定義代價函數，這里我們使用均方誤差。然后，計算代價函數關于每個參數的梯度。
我們隨意給出一組數據：
（1，2），（2，4），（3，6）
我們的目的是盡量用y=wx+b去擬合這些數據。w梯度計算公式是：

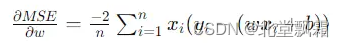
b的則是

w=0,b=0得出得梯度分別是： -56/3和 -8。
這個線性模型是一條 y=0的直線，顯然無法擬合這些數據.我們此時設置 w=0.1，b=0.1來擬合，又得到了兩個梯度，可能這次的線性模型擬合度會好一些，那么再設置w=0.2,b=0.2，會不會又好一點呢？我們每次選用w,b都會得到一個預測值，然后我們可以算出他的代價函數（誤差）值，我們就可以畫出這樣一張圖。

其中我們要找的點就是誤差最低的那一個點，我們可能會從任何地方出發，去找那個點，這個過程運用到的就是梯度下降算法

正式介紹

通過上面那個小例子，我們已經知道了，梯度下降算法常用于最小化代價函數（或損失函數），以此來優化模型的參數。代價函數衡量的是模型預測值與實際值之間的差異。通過最小化這個函數，我們可以找到模型預測最準確的參數。

抽象

我們可以抽象這個過程：想象一下，你在山頂，目標是以最快的速度下到山腳。因為你被蒙上了眼睛，看不見周圍的環境，所以你只能通過感覺腳下的坡度來判斷下一步該往哪個方向走。這個“感覺坡度”的過程，就有點像梯度下降算法的工作原理。

梯度的含義

“梯度”（Gradient）其實就是指函數在某一點上的斜率，或者說是這一點最陡的上升方向。梯度告訴你，如果你想讓函數值增加得最快，應該往哪個方向走。相應地，梯度的反方向就是函數值下降最快的方向。

梯度下降的工作原理

梯度下降算法的核心思想就是：在當前位置計算梯度（即斜率），然后沿著梯度的反方向走一小步，重復這個過程，直到到達山腳（即找到函數的最小值點）。

梯度下降–專屬案例

假設我們有一個函數
y=x^2這個求最小值，這個案例不是讓你使用高中數學去解答，你可以不假思索回答是0，但是不是我想要學習的。
讓我們以梯度下降的方式求解，初始化: 假設我們隨機選擇一個起點，x=2。計算梯度: 對f(x) 求導得到它的梯度 f(x)=2x。在x=2 處的梯度是4。此時我們更新x，我們假設我們走一小步，0.1那么此時x應該是：x = x - 學習率 * 梯度 = 2 - 0.1 * 4 = 1.6 計算此時的梯度，重復這個過程，直到x的更新值很小很小，無限趨近于0，此時實際上x的值(在y=x^2中)也無限趨近于0，y也趨近于0了。

注意事項

學習率的選擇：學習率太大可能導致“跨過”最低點，甚至發散；學習率太小又會導致收斂速度很慢。因此，選擇一個合適的學習率非常關鍵。收斂條件：通常會設置一個閾值，當連續兩次迭代的x值變化非常小（小于這個閾值）時，我們就認為算法已經收斂。

結束

我們計算房價，假設線性模型，求w,b，我們使用均方誤差（MSE）作為代價函數，來衡量模型預測值與實際值之間的差異，我們使用梯度下降模型計算w,b的梯度，得到了誤差，我們通過控制迭代次數和學習率，不斷的修改w,b，以使得誤差越來越小，誤差越來越小，即w，b的變化非常小或達到一個預設的迭代次數。這就是梯度下降算法。對于不同類型的機器學習問題，成本函數的選擇也會不同。例如：回歸問題：常用的成本函數是均方誤差（Mean Squared Error, MSE），它計算的是預測值與實際值之間差異的平方的平均值。這個值越小，表示模型的預測越準確。分類問題：對于二分類問題，一個常見的成本函數是交叉熵（Cross-Entropy），它量化的是實際標簽與預測概率之間的差異。
在梯度下降算法中，我們的目標是找到模型參數的值，這些參數值能使成本函數的值最小化。換句話說，我們希望找到的參數能讓模型的預測盡可能接近實際情況，從而最小化誤差。通過迭代地更新模型參數，梯度下降算法能夠逐步逼近這個最優參數組合，實現成本的最小化。