給你一棵二叉樹的根節點 root ，找出并返回滿足要求的節點數，要求節點的值等于其 子樹 中值的 平均值 。

注意：

n 個元素的平均值可以由 n 個元素 求和 然后再除以 n ，并 向下舍入 到最近的整數。
root 的 子樹 由 root 和它的所有后代組成。

示例 1：

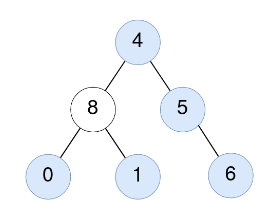
輸入：root = [4,8,5,0,1,null,6]
輸出：5
解釋：
對值為 4 的節點：子樹的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
對值為 5 的節點：子樹的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
對值為 0 的節點：子樹的平均值 0 / 1 = 0 。
對值為 1 的節點：子樹的平均值 1 / 1 = 1 。
對值為 6 的節點：子樹的平均值 6 / 1 = 6 。
示例 2：

輸入：root = [1]
輸出：1
解釋：對值為 1 的節點：子樹的平均值 1 / 1 = 1。

提示：

樹中節點數目在范圍 [1, 1000] 內
0 <= Node.val <= 1000

遞歸dfs后序遍歷模擬：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int averageOfSubtree(TreeNode* root) {int ans = 0;getNumAndSum(root, ans);return ans;}private:vector<int> getNumAndSum(TreeNode *node, int &ans){if (node == nullptr){return {0, 0};}vector<int> left = getNumAndSum(node->left, ans);vector<int> right = getNumAndSum(node->right, ans);ans += static_cast<int>((left[1] + right[1] + node->val) / (left[0] + right[0] + 1)) == node->val;return {left[0] + right[0] + 1, left[1] + right[1] + node->val};}
};

如果樹中有n個節點，則此算法時間復雜度為O(n)，空間復雜度為O(lgn)。