1. 串
1.1 串的定義
ADT String{
數據對象:D={ai|ai∈CharacterSet, i=1, 2, …, n, n≧0}
數據關系:R1={|ai-1, ai∈D, i=2, …, n}
基本操作:
生成一個值等于chars的串
復制一個串
判斷串是否空串
比較串的大小
返回串元素的個數
將串清空
將串合并
返回串的指定下標的元素之后指定長度的字串
在某個串中查找規定子串,并返回指定下標的字符后第一次出現的位置
在某個串中用規定字串替代不重疊的另一規定字串
在串的指定下標的字符前插入一個指定子串
在串中刪除一個規定下標開始指定長度的字串
銷毀串
}1.2 串的存儲結構
1.2.1 順序存儲
//----------串的定長順序存儲結構---------------
#define MAXLEN 255 //串的最大長度
typedef struct
{
char ch[MAXLEN+1]; //存儲串的一維數組,從下標為1開始存儲
int length; //串的當前長度
}SString;
//----------串的堆式順序存儲結構,按需分配長度----------------
typedef struct
{
char *ch; //如果是非空串,則按照串長分配存儲區,否則ch為null
int length; //串的當前長度
}HString;1.2.2 鏈式存儲
#define CHUNKSIZE 80
typedef struct Chunk
{
char ch[CHUNKSIZE]; //提高空間利用率(一個結點多個字符)
struct Chunk *next; //最后一個結點不滿用非串字符填滿
}Chunk;
typedef struct
{
Chunk *head, *tail; //尾指針便于操作
int length; //串的當前長度
}LString;1.3 模式匹配算法
1.3.1 BF算法
int Index_BF(SString S, SString T, int pos)
{//返回模式T在主串S中第pos個字符開始第一次出現的位置。若不存在,則返回值為0
//T非空,0int i=pos; int j=1; //初始化while (i<=S.length && j<=T.length) //如果兩個串均沒到串尾{if (S.ch[i]==T.ch[j]){++i; ++j;} //如果目前的字符匹配,則繼續比較下一個字符else{i=i-j+2; j=1;} //如果失配,則將i退回到主串開始比較的下一個字符,j退回到字串的開頭}if (j>T.length) return (i-T.length); //匹配成功else return 0; //匹配失敗 }1.3.2 KMP算法
設計思想
失配時,主串指示器i不用回溯,利用已經得到的部分匹配,將模式串指示器j向右滑動盡可能遠的距離后繼續比較
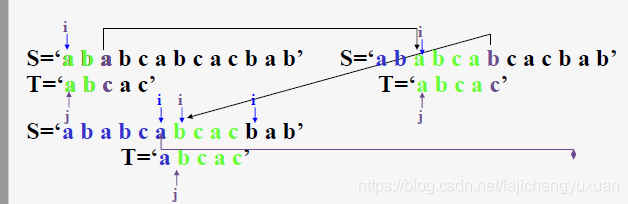


為此定義next函數,表示模式中第j個字符失配時,在模式串中需要重新與主串中該字符進行比較的字符的位置
故算法如下
int Index_KMP(SString S, SString T, int pos)
{ //利用模式串T的next函數求T在主串S中第pos個字符之后的位置
//其中T非空,1<=pos<=S.length
int i=pos; int j=1;
while (i<S.length && j<T.length) //兩個串均未到達串尾
{
if(j==0 || S.ch[i]==T.ch[j]){++i; ++j;} //如果j為0或者目前的字符匹配,則繼續比較下一個字符
else j=next[j]; //否則就將j置為next[j]
}
if (j>T.length) return (i-T.length); //匹配成功
else return 0; //匹配失敗
}next函數求法
遞推求值
由定義知,
next[1] = 0
設next[j]=k,表明有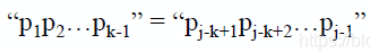
1k滿足上式,此時next[j+1]的值有以下兩種情況
(1)pk=pj,則有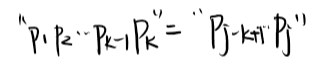
故
next[j+1]=k+1=next[j]+1
(2)pk≠pj
此時用把求next值的問題看成模式匹配的問題,模式串既是主串又是模式串
求next[j+1],第j+1個字符與主串失配,假設此時將k=next[j]及其前面的字符串滑過來與主串匹配,由于pk≠pj,此時第k個字母與主串失配,因此我們應當在它前面尋找k’=next[k]繼續與主串匹配,以此類推,直到某個字符匹配成功或p[k+1]=1
故
next[j+1]=next[k]+1
算法如下:
void get_next(SString T, int next[])
{//求模式串T的next函數值并存入數組next
int i=1;next[1]=0;int j=0;
while (i<T.length)
{
if(j==0||T.ch[i]==T.ch[j]){++i; ++j; next[i]=j;} //如果j是0(開頭)或者第i個字符等于第j個字符,則next[i+1]=j+1
else j=next[j]; //如果不等于,j回溯到next[j]
}
}但是,例如串"aaaab"與"aaabaaaab",第4個字母失配,但是還要將j=3,2,1依次與i=4比較,但由于j=1,2,3,4的字符都相等且i=4字符與j=4字符不等,因此可以直接比較i=5和j=1。
由此可見,當next[j]=k,而tj=tk時,不必比較,可以直接比較tj和tnext[k],以此類推
算法如下:
void get_nextval(SString T, int nextval[])
{//求模式串中next函數的修正值并存入數組nextval
int i=1;nextval[1]=0;int j=0;
while (i<T.length)
{
if(j==0||T.ch[i]==T.ch[j]){
++i;++j;
if(T.ch[i]!=T.ch[j]) nextval[i]=j;
else nextval[i]=nextval[j]; //如果第i個字符與第j個字符相等,j回溯到nextval[j]
}
else j=nextval[j];
}
}2. 數組
2.1 定義
ADT Array{
數據對象:ji = 0, …, bi-1, i=1,2,…,n
D = {aj?j?…jn | n>0 稱為數組的維數,bi是第i維的長度}
ji是數組元素第i維下標,aj?j?…jn∈ElemSet}
數據關系:R = {R1, R2, …, Rn}
Ri = {}}
0<=jk<=bk-1, 1<=k<=n 且k≠i
0<=ji<=bi-2
aj?…ji…jn, aj?…ji+1…jn∈D, i = 2, …, n}
基本操作:
構造數組
銷毀數組
賦值指定的元素
返回指定的元素值
}2.2 數組的順序存儲
位置下標:LOC(i,j)=LOC(0,0)+(n*i+j)L(可推廣至n維)
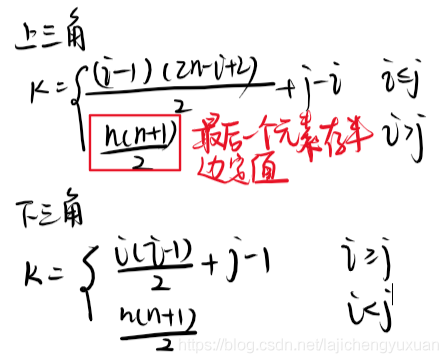
2.3 特殊矩陣的壓縮
對稱矩陣(aij = aji)
以sa[a(a+1)/2]存儲下三角,則對于下標k有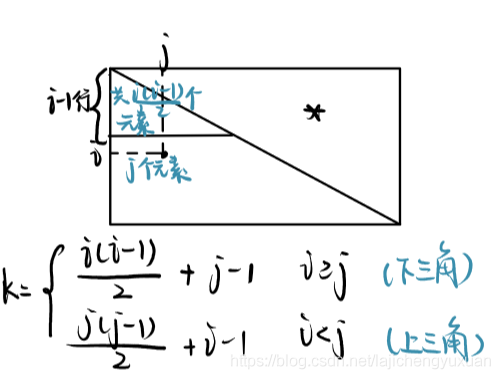
三角矩陣(只有半邊有元素,剩下半邊元素值相等)
其它矩陣
(1)對角矩陣:找規律,壓縮
(2)稀疏矩陣:三元組表(行下標,列下標,值)
3. 廣義表
3.1 定義
一些結論
(1)元素可以是原子或者子表
(2)可以為其它廣義表共享,可以共享其它廣義表
(3)廣義表是一個遞歸的表重要運算
(1)取表頭:取出非空廣義表的第一個元素,可以是單原子或者子表
(2)取表尾:取出除了第一個元素之外,其余元素構成的表
3.2 存儲結構
表結點由標志域(1表示表結點,0表示原子結點),表頭結點,表尾結點組成,原子由標志域和和值組成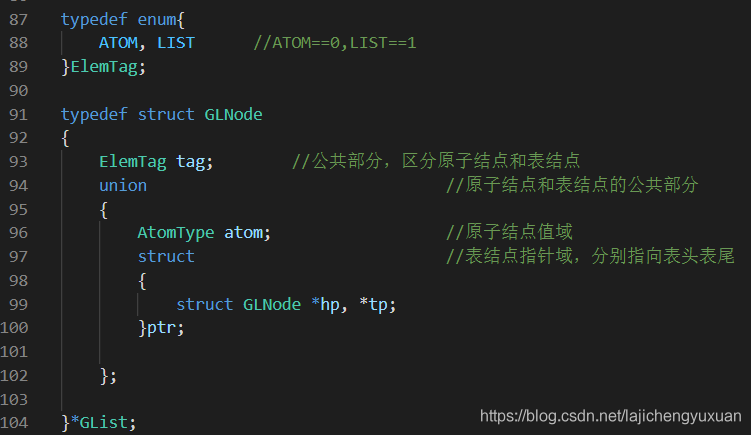
(a,(b,c,d))結構圖示如下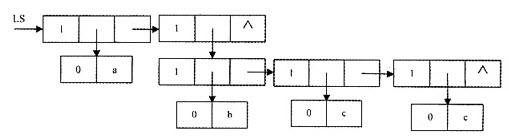

方法及示例)

方法與示例)
![[轉載] 中國象棋軟件-引擎實現(一)概述](http://pic.xiahunao.cn/[轉載] 中國象棋軟件-引擎實現(一)概述)
方法與示例)
)

方法與示例)


方法(帶示例))

方法(帶示例))

方法及示例)


方法及示例)
