本節書摘來自異步社區《精通Matlab數字圖像處理與識別》一書中的第6章,第6.2節,作者 張錚 , 倪紅霞 , 苑春苗 , 楊立紅,更多章節內容可以訪問云棲社區“異步社區”公眾號查看
6.2 傅立葉變換基礎知識
精通Matlab數字圖像處理與識別
要理解傅立葉變換,掌握頻率域濾波的思想,必要的數學知識是不能跳過的。為便于理解,我們將盡可能定性地去描述。其實傅立葉變換所必需的數學知識對于一個理工科大學二年級以上的學生來說是很有限的,高等數學中傅立葉級數的知識加上線性代數中基和向量空間的概念就足夠了。下面就從一維情況下的傅立葉級數開始進行介紹。
6.2.1 傅立葉級數
法國數學家傅立葉發現任何周期函數只要滿足一定條件(狄利赫里條件)都可以用正弦函數和余弦函數構成的無窮級數,即以不同頻率的正弦和余弦函數的加權和來表示,后世稱為傅立葉級數。
對于有限定義域的非周期函數,可以對其進行周期拓延,從而使其在整個擴展定義域上為周期函數,從而也可以展開為傅立葉級數。
1.傅立葉級數的三角形式
周期為T的函數f (t)的三角形式傅立葉級數展開為

a k和b k稱為傅立葉系數。稍后在學習傅立葉級數的復數形式時還將介紹傅立葉系數的另一種形式。事實上,傅立葉系數正是我們在6.2.2小節傅立葉變換中所關心的對象。
于是,周期函數f(t)就與下面的傅立葉序列產生了一一對應,即
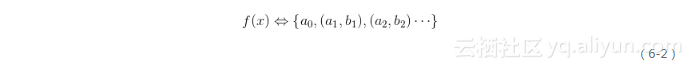
圖6.1所示形象地顯示出了這種頻率分解,左側的周期函數f(x)可以由右側函數的加權和來表示,即由不同頻率的正弦和余弦函數以不同的系數組合在一起。
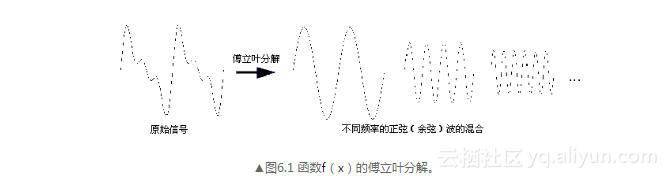
原函數f(x)(左),其傅立葉展開為一系列不同頻率的正弦、余弦函數的加權和(右)
從數學上已經證明了,傅立葉級數的前N項和是原函數f(t)在給定能量下的最佳逼近。
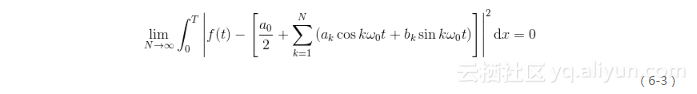
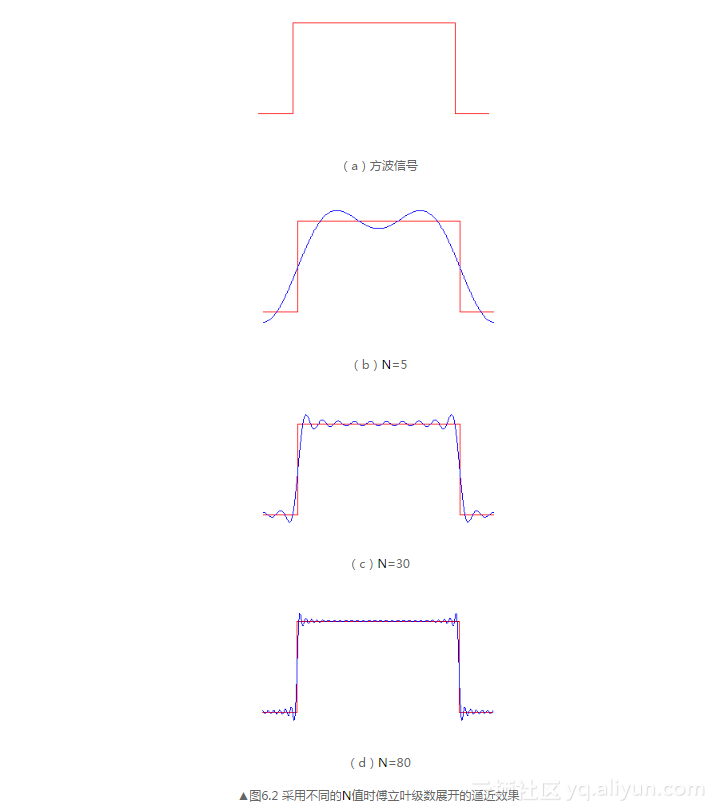
圖6.2為我們展示了對于一個方波信號函數采用不同的N值的逼近情況。隨著N的增大,逼近效果越來越好。但同時也注意到,在f (x)的不可導點上,如果只取式(6-1)右邊的無窮級數中的有限項之和作為hat f(x),那么hat f(x)在這些點上會有起伏,對于圖6.2(a)的方波信號尤為明顯,這就是著名的吉布斯現象。
2.傅立葉級數的復指數形式
除上面介紹的三角形式外,傅立葉級數還有其他兩種常用的表現形式,即余弦形式和復指數形式。借助歐拉公式,上述3種形式可以很方便地進行等價轉化,本質上它們都是一樣的。
復指數傅立葉級數即我們經常說的傅立葉級數的復數形式,因其具有簡潔的形式(只需一個統一的表達式計算傅立葉系數),在進行信號和系統分析時通常更易于使用;而余弦傅立葉級數可使周期信號的幅度譜和相位譜意義更加直觀,函數的余弦傅立葉級數展開可以解釋為f(x)可以由不同頻率和相位的余弦波以不同系數組合在一起來表示,而在三角形式中相位是隱藏在系數a n和b n中的。下面主要介紹復指數傅立葉級數,在后面的傅立葉變換中要用到的正是這種形式。關于余弦傅立葉級數的有關知識,感興趣的讀者請參考附錄Ⅲ。
傅立葉級數的復指數形式為
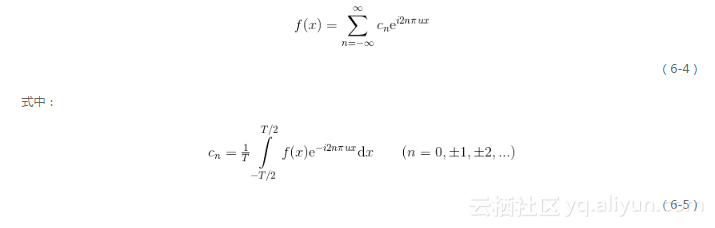
由式(6-4)和(6-5)可見,復指數傅立葉級數形式比較簡潔,級數和系數都可以采用一個統一的公式計算。有關如何由式(6-1)推導出傅立葉級數復指數形式(6-4)的過程,由于這里我們感興趣的并非傅立葉級數本身,就不在正文中給出了,詳細的內容可參考附錄Ⅱ,只要您相信不同的展開形式之間本質上是等價的,并對復指數形式的傅立葉級數展開建立了一個基本的形式上的認識就足以繼續閱讀和理解后面的內容了。
6.2.2 傅立葉變換
1.一維連續傅立葉變換
對于定義域為整個時間軸(-∞
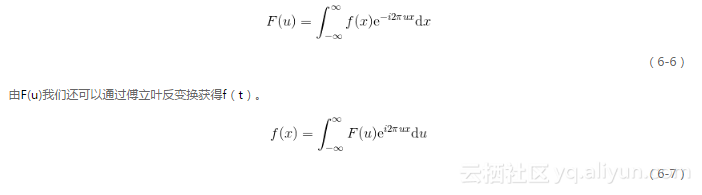
式(6-6)和式(6-7)即為我們通常所說的傅立葉變換對,6.1節中提到的函數可以從它的反變換進行重建正是基于上面的傅立葉變換對。
由于傅立葉變換與傅立葉級數涉及兩類不同的函數,在很多數字圖像處理的書中通常對它們分別進行處理,并沒有闡明它們之間存在的密切聯系,這給很多初學者帶來了困擾,實際上我們不妨認為周期函數的周期可以趨向無窮大,這樣可以將傅立葉變換看成是傅立葉級數的推廣。
仔細地觀察式(6-6)和式(6-7),對比復指數形式的傅立葉級數展開公式式(6-4),注意到在這里傅立葉變換的結果F(u)實際上相當于傅立葉級數展開中的傅立葉系數,而反變換公式式(6-7)則體現出不同頻率復指數函數的加權和的形式,相當于復指數形式的傅立葉級數展開公式,只不過這里的頻率u變為了連續的,所以加權和采用了積分的形式。這是因為隨著作為式(6-5)的積分上下限的T向整個實數定義域擴展,即T→∞,頻率u則趨近于du(因為u=1/T),導致原來離散變化的u的連續化。
2.一維離散傅立葉變換
一維函數f(x)(其中x=0, 1, 2 ,… , M-1)的傅立葉變換的離散形式為
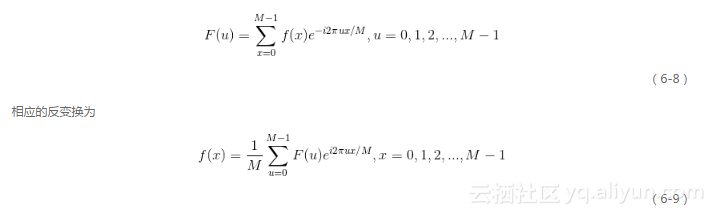
由于一維情況下很多性質更為直觀,我們更青睞于分析一維離散傅立葉變換,而由此得出的這些結論都可順利推廣至二維。一些有用的性質如下。
仔細觀察式(6-8)和式(6-9),注意到在頻域下變換F(u)也是離散的,且其定義域仍為0~M-1,這是因為F(u)的周期性,即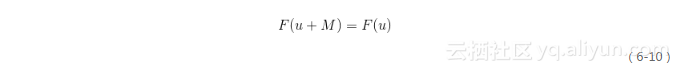
考慮式(6-9)中的系數1/M,在這里該系數被放在反變換之前,實際上它也可以位于式(6-8)的正變換公式中。更一般的情況是只要能夠保證正變換與反變換之前的系數乘積為1/M即可。例如,兩個公式的系數可以均為 1/sqrt M 。
為了求得每一個F(u)(u=0, 1, 2,…, M-1),都需要全部M個點的f(x)參與加權求和計算。對于M個u,則總共需要大約M2次計算。對于比較大M(在二維情況下對應著比較大的圖像),計算代價還是相當可觀的,我們會在下一節快速傅立葉變換中來研究如何提高計算效率的問題。
3.二維連續傅立葉變換
有了之前的基礎,下面我們將傅立葉變換及其反變換推廣至二維。對于二維連續函數,傅立葉變換為
F(u,v) = int_{ - infty }^infty {int_{ - infty }^infty {f(x,y)text{e}^{ - text{j}2pi (ux + vy)} dxdy} }
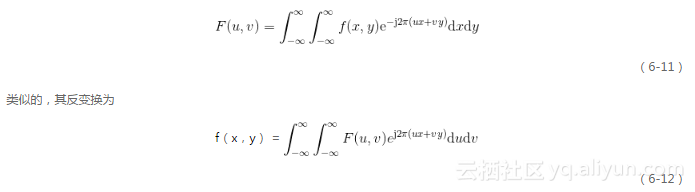
4.二維離散傅立葉變換
在數字圖像處理中,我們關心的自然是二維離散函數的傅立葉變換,下面直接給出二維離散傅立葉變換(Discrete Fourier Transform, DFT)公式。

顯然,這是f(x, y)各個像素的灰度之和。而如果將系數1/MN放在正變換之前,則F(0, 0)對應于原圖像f(x, y)的平均灰度。F(0, 0)有時被稱作頻譜的直流分量(DC)。
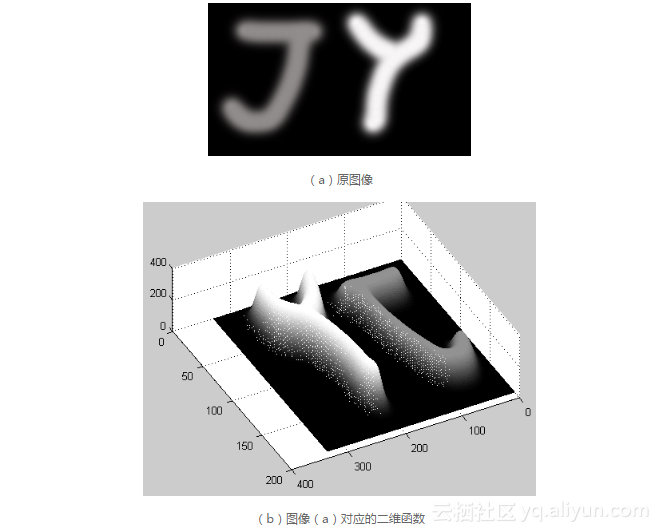
我們之前曾指出了一維函數可以表示為正弦(余弦)函數的加權和形式;類似的,二維函數f(x, y)可以分解為不同頻率的二維正弦(余弦)平面波的按比例疊加。圖6.3(a)中給出了一幅簡單的圖像,可將它視為以其灰度值作為幅值的二維函數,如圖6.3(b)所示,根據式(6-13),它可以分解為如圖6.3(c)所示的不同頻率和方向的正弦(余弦)平面波的按比例疊加(只給出了一部分)。比如圖6.3(c)中第一行中間的平面波為sin(Y),而第二行右面的平面波則為sin(X+2Y),而第三行最后的一個為sin(2X+2Y)。

6.2.3 幅度譜、相位譜和功率譜
下面,我們再來定義傅立葉變換的幅度譜、相位譜以及功率譜。

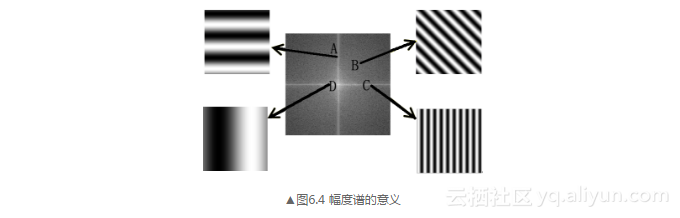
幅度譜又叫頻率譜,是圖像增強中關心的主要對象,頻域下每一點(u,v)的幅度|F(u, v)|可用來表示該頻率的正弦(余弦)平面波在疊加中所占的比例,如圖6.4所示。幅度譜直接反映頻率信息,是頻域濾波中的一個主要依據。
圖6.4所示幅度譜中的A、B、C、D四點的幅值分別為四周的4個正弦平面波在的加權求和中的權值(混合比例)。注意這4個正弦平面波的方向和頻率。
相位譜表面上看并不那么直觀,但它隱含著實部與虛部之間的某種比例關系,因此與圖像結構息息相關。
由于對于和空域等大的頻域空間下的每一點(u, v),均可計算一個對應的|F(u, v)|和φ(u, v),因此可以像顯示一幅圖像那樣顯示幅度譜和相位譜。圖6.5(b)、(c)分別給出了圖6.5(a)中圖像的幅度譜和相位譜,獲得它們的方法請參考6.3節中傅立葉變換實現的相關內容,關于幅度譜和相位譜的一個非常有趣的例子請參考例6.2。

▲圖6.5 circuit.tif幅度譜和相位譜。幅度譜和相位譜都將(0,0)點移到了中心
6.2.4 傅立葉變換的實質—基的轉換
無論是傅立葉變換、離散余弦變換還是小波變換,其本質都是基的變換。下面首先讓我們一起回顧一下線性代數中基和向量空間的相關知識。
1.基和向量空間
在三維歐氏向量空間中,某向量vec v 可以由3個復數{v_1 ,v_2 ,v_3 }來定義,常常記作vec v =(v_1 ,v_2 ,v_3 ),這3個復數與3個正交單位向量{vec e_1 ,vec e_2 ,vec e_3 }相聯系。實際上,有序集{ v_1 ,v_2 ,v_3 }表示向量 vec v 的3個標量分量,也就是系數;而3個正交單位向量{vec e_1 ,vec e_2 ,vec e_3 }即為該三維歐氏空間的基向量。我們稱該空間為這3個基向量所張成的空間,任何該空間中的向量vec v 均可由這3個基向量的線性組合(加權和)表示為

在上面的敘述中涉及了向量的正交,這是向量代數中一個非常重要的概念。為了說明正交的概念,讓我們首先回顧一下向量點積(數量積),兩個向量的點積定義為

此時,如果vec u bullet vec v = 0 ,則稱這兩個向量vec u 和vec v 互相正交。由式(6-22)可知,兩非零向量正交則cos theta = 0 ,說明其夾角為90(垂直)。
接下來,定義一個向量在另一個向量方向上的投影或分量為

式中:vec e_v 為向量vec v 單位化后的單位向量,模為1,方向與vec v 相同。式(6-23)說明如果需要得到某向量在給定方向上的分量,只需計算該向量與給定方向單位向量的點積。
圖6.6能夠幫助我們理解上述內容,圖6.6(a)中為一個三維空間中的向量vec v 以及3個單位正交基向量vec e_1 ,vec e_2 ,vec e_3 ;圖6.6(b)中給出了向量vec v 在vec e_2 方向的投影v_2 ;在圖6.6(c)中,根據矢量加法的平行四邊形法則,向量vec v 被分解為3個正交基向量vec e_1 ,vec e_2 ,vec e_3 線性組合,顯然可以表示為vec v =(v_1 ,v_2 ,v_3 )的形式。
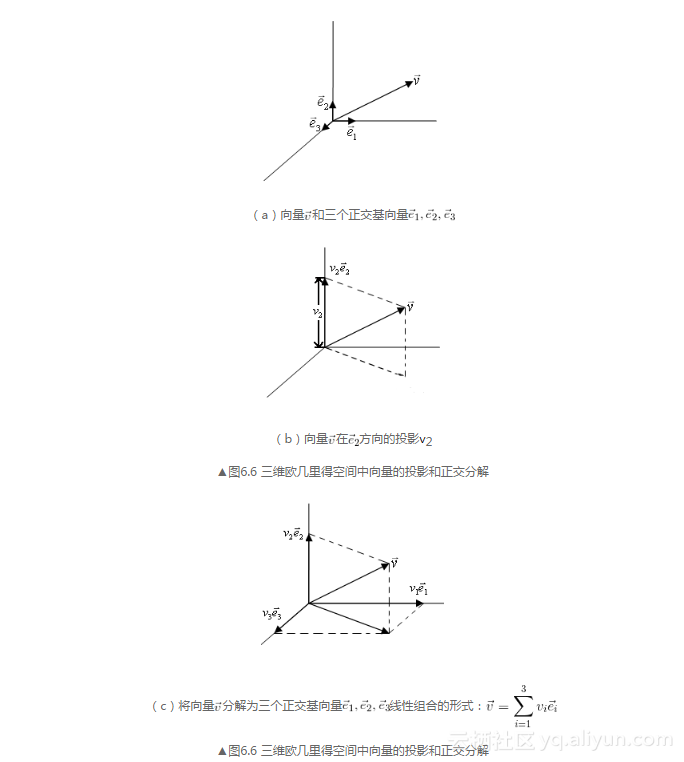
將三維向量空間中基與投影的概念推廣至N維向量空間。任何一個該空間中的N×1向量均可由N個基向量vec e_1 ,vec e_2 ,...,vec e_N 的線性組合來表示,記作

2.基函數和函數空間
盡管上面的向量分解與重構的問題比較基礎,但它與傅立葉變換與反變換之間的關系卻十分緊密。事實上,它們在形式上有著驚人的相似,唯一不同的是這里的向量空間變成了函數空間,向量vec v 變成了函數f(x),而基向量vec e 1,vec e 2,…,vec e n也相應地變成了基函數。對比式(6-24)~(6-25)和式(6-8)~(6-9)的形式不難看出,式(6-25)的分解過程即相當于傅立葉變換,而式(6-26)的重構過程則恰恰相當于傅立葉反變換。也就是說,相應函數空間中的任意函數均可以由該函數空間中的一組基函數的加權和來表示。觀察式(6-8)容易發現,這里的基函數的形式為text{e}^{ - i2pi ux} ,我們用下面的等式來表示函數的正交性。
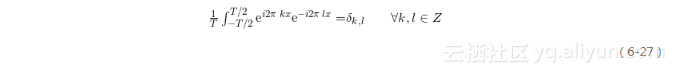
至此,讀者應該已經理解了傅立葉變換的實質——基的轉換。對于給定函數f(x),關鍵是選擇合適的基,使得f(x)在這組基下表現出我們需要的特性。當某一組基不滿足要求時,就需要通過變換將函數轉換到另一組基下表示,方可得到我們需要的函數表示。常用的變換有傅立葉變換(以正弦和余弦函數為基函數)、小波變換(以各種小波函數為基函數)、離散余弦變換以及Walsh變換等。實際上,我們在第12章中將指出,特征降維中常用的主成份分析法(K-L變換)本質上也是一種基的轉換。

:java內存分析工具-MAT和OQL)

![obj[]與obj._Ruby中帶有示例的Array.include?(obj)方法](http://pic.xiahunao.cn/obj[]與obj._Ruby中帶有示例的Array.include?(obj)方法)

方法)

...)
》——2.11節秘訣:構建星星滑塊)



用法及代碼示例)

》——導讀)




