注：本文比較硬核但是很值得大家花心思看完，看完你一定會有所收獲的
紅黑樹是面試中一個很經典也很有難度的知識點，網傳字節跳動面試官最喜歡問這個問題。很多人會覺得這個知識點太難，不想花太多功夫去了解，也有人會認為這個數據結構在日常開發中使用的很少，因此沒必要多做掌握。
在此我針對以上兩個觀點做出一些糾正：首先，紅黑樹這個數據結構確實復雜，但是還沒有到完全無法理解的地步。網上大多博客都不能夠清晰完整的描述出紅黑樹的整個體系，對于紅黑平衡調整的細節部分也沒有很詳盡的介紹，因此給學習帶來了較大的困難。
其次，諸如Java中HashMap的底層實現，在JDK1.8中為了解決過度哈希沖突帶來的長鏈表，會將鏈表轉為紅黑樹；Linux底層的CFS進程調度算法中，vruntime利用紅黑樹來進行存儲；多路復用技術的Epoll的核心結構也是紅黑樹+雙向鏈表。
我們不會直接去手寫一個可用的紅黑樹，但是了解紅黑樹的結構，有助于我們去理解一些底層具體實現。與此同時，紅黑樹也是對樹結構的一種高度綜合運用，涉及到多叉樹，樹平衡調整，節點旋轉等等，這些是對數據結構基本功的最佳歷練。

其實當面試官提出這個問題的時候，不參照答案，他大概率也無法清晰的給出具體的定義和操作。但是他希望從這個問題出發，看到你對于一個數據結構的理解，考察你知識面的廣度和深度。能否給出完整的定義，能否介紹自己對紅黑樹的認識，能否通過旋轉，染色等操作在給定的場景下對一顆紅黑樹進行調整使其符合定義......這些才是面試官希望從你的答案中得到的信息，問了一圈身邊大廠的面試官朋友，跟我這個說法出入不大。
讀完這篇文章，你將能夠從紅黑樹的概念模型2-3-4樹出發，理解紅黑樹五大定義背后的邏輯。你也可以深刻認識到紅黑節點顏色背后的意義，對于插入刪除引發的動態變化有一定的認識，而不再是去硬性的記憶某個場景下的調平操作（諸如：刪除某節點，當該節點的叔父節點為紅，而叔父節點的左右子節點都為黑的情況下，我們應該......）。你能夠掌握節點旋轉的具體操作，理解染色的目的。
最后，如果你足夠認真，配圖中有清晰的插入刪除全部步驟，你能夠真正的將紅黑樹變成自己的知識。先談平衡樹
做開發的朋友一定知道接口這個東西：定義接口，給出實現。一個接口可以有多種不同的實現，但是這些實現都會滿足接口中的聲明。
例如，我們定義手機是一個可用作通訊的工具，作為它的實現，三星，蘋果，華為推出了各式各樣的產品。
紅黑樹的本質其實也是對概念模型：2-3-4樹的一種實現，因此我們先來關注2-3-4樹。
2-3-4樹是階數為4的B樹，B樹，全名BalanceTree，平衡樹。這種結構主要用來做查找。
關于B樹（平衡多路查找樹）的定義，網上已經有很多介紹，在此不多贅述。它最重要的特性在于平衡，這使得我們能夠在最壞情況下也保持O(LogN)的時間復雜度實現查找（一個不具備平衡性的查找樹可能退化成單鏈表，時間復雜度會到O（N））。
“ 在此需要提醒大家一下，平衡的定義是說從空鏈接到根節點距離相等，此處一定要用心理解。（也就是說非葉子節點是不會存在空鏈接的）
由于2-3-4樹是一顆階數為4的B樹，所以它會存在以下節點：

• 2節點
• 3節點
• 4節點

2節點中存放著一個key[X]，兩個指針，分別指向小于X的子節點和大于X的子節點；3節點中存放在兩個key[X,Y],三個指針，分別指向小于X的子節點，介于X~Y之間的子節點和大于Y的子節點；4節點可依此類推。

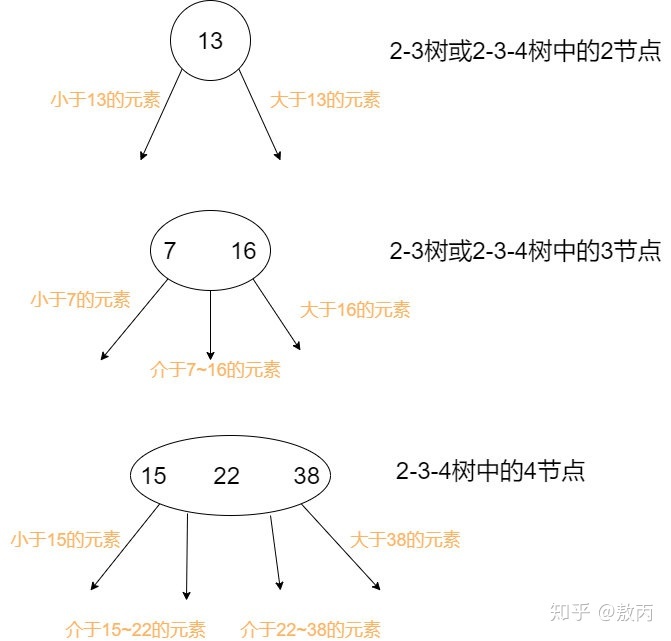
2-3-4樹到紅黑樹的轉化
紅黑樹是對概念模型2-3-4樹的一種實現，由于直接進行不同節點間的轉化會造成較大的開銷，所以選擇以二叉樹為基礎，在二叉樹的屬性中加入一個顏色屬性來表示2-3-4樹中不同的節點。
2-3-4樹中的2節點對應著紅黑樹中的黑色節點，而2-3-4樹中的非2節點是以紅節點+黑節點的方式存在，紅節點的意義是與黑色父節點結合，表達著2-3-4樹中的3，4節點。
（此處理解成紅節點也好，紅色鏈接也好，看個人喜好。很多書中會說是由黑色節點指出的紅色鏈接，鏈接指向的節點顏色為紅。）
我們先看2-3-4樹到紅黑樹的節點轉換。2節點直接轉化為黑色節點；3節點這里可以有兩種表現形式，左傾紅節點或者右傾紅節點。而4節點被強制要求轉化為一個黑父帶著左右兩個紅色兒子。

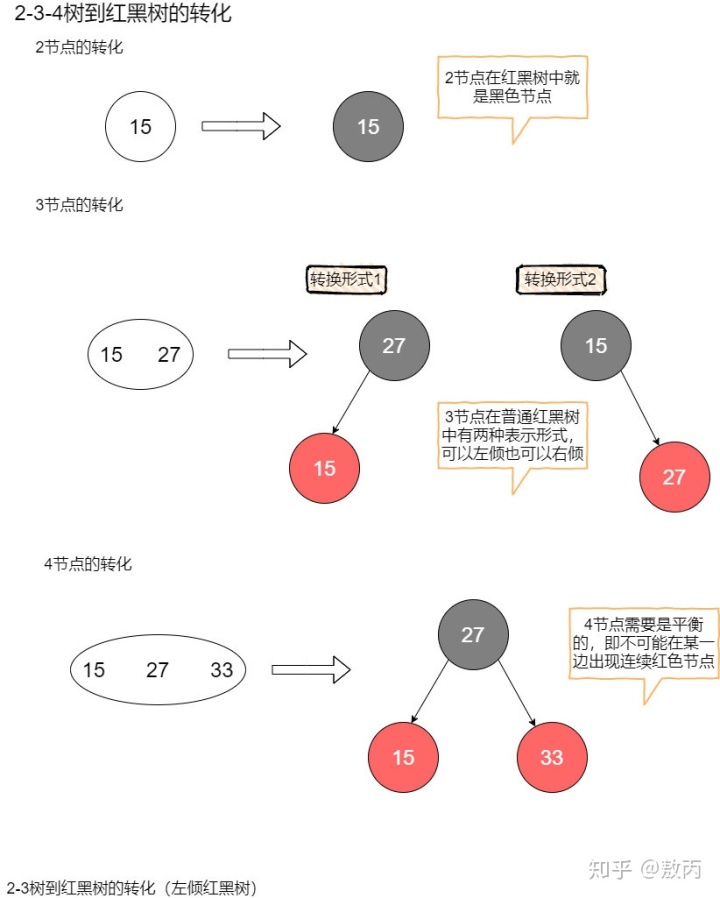
本文的研究主體是2-3樹（原因會在后文給出），并且是2-3樹中較為特殊的一種轉化--左傾紅黑樹。顧名思義，左傾紅黑樹限制了如果在樹中出現了紅色節點，那么這個節點必須是左兒子。
以下是它的轉化過程：

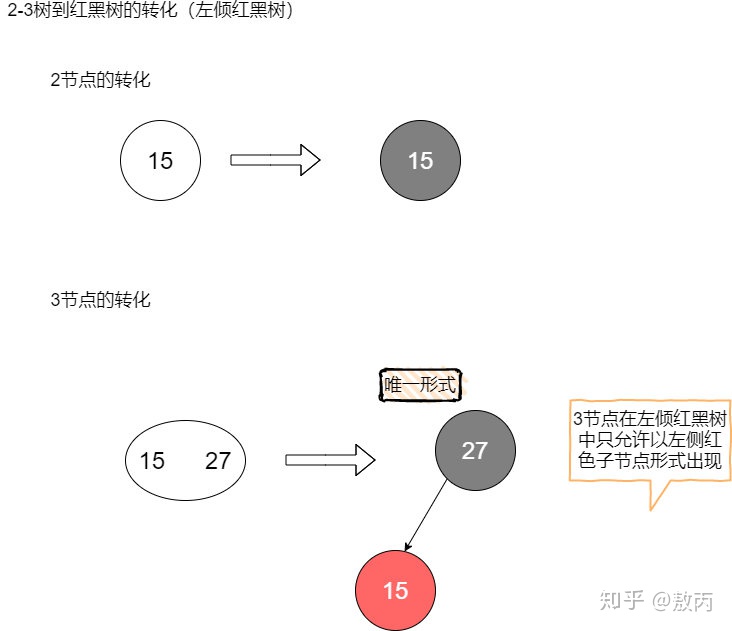
光看單個節點的轉化可能還不夠明顯，我制作了一張紅黑樹轉2-3樹的示意圖，很清晰地描繪了它們之間的關系。
只要把左傾紅黑樹中的紅色節點順時針方向旋轉45°使其與黑父平行，然后再將它們看作一個整體，你就會發現，這不就是一顆2-3樹嗎？

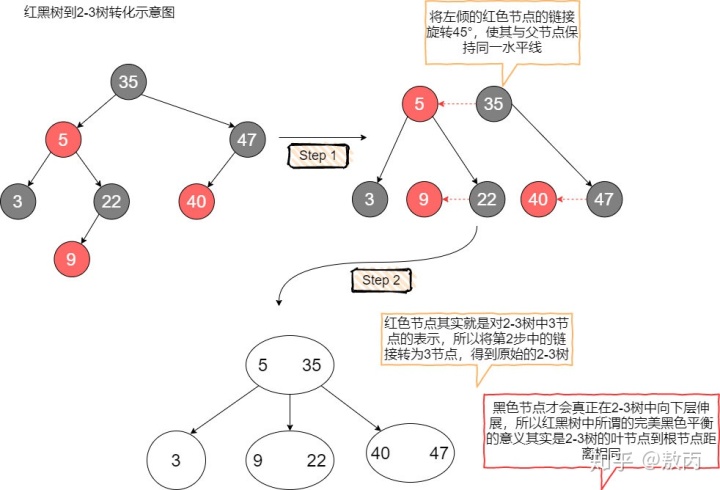
至此，我想大家已經明白，紅黑樹其實就是對概念模型2-3樹（或者2-3-4樹）的一種實現。
算法導論中給出的是紅黑樹基于2-3-4樹實現，其中4節點要求平衡（即4節點必須用黑色父親和左右兩個紅色兒子表示，紅色兒子不能出現在同一邊）。
算法4中給出的紅黑樹是基于2-3樹實現，而且這種實現的紅黑樹十分特殊，它要求概念模型中的3節點在紅黑樹中必須用左傾的紅色節點來表示。這種限定能夠很大的減少紅黑樹調整過程中的復雜性，我們將在接下來的內容中體會到這一點。
我將算法導論和算法4中的紅黑樹反復的看了幾遍，最終選擇算法4中的紅黑樹做演示主體。

• 首先，算法4中的紅黑樹基于2-3樹概念模型，不用考慮2-3-4樹中復雜的4節點分裂；
• 第二，算法4中的紅黑樹是左傾紅黑樹，進一步降低了調平的難度；
• 第三，算法導論中對于紅黑樹刪除場景的闡述并不夠具體，許多關鍵環節都用“經過一定的旋轉和變色處理”來帶過，不利于新手的學習。（我花了很長時間還原具體過程）。
  考慮到部分讀者有充足的精力研究以2-3-4樹為概念模型的紅黑樹，在介紹2-3樹的同時也會帶上2-3-4樹的基礎知識，幫助學有余力的讀者去理解算法導論中的紅黑樹。（所以如果沒有必要，只看2-3樹的部分就行）。

我們在了解紅黑樹的插入刪除操作之前，需要先了解2-3樹的插入刪除操作，這樣才能理解紅黑樹中染色和旋轉背后的意義。
讓我們來看一下對于2-3樹的插入。我們的插入操作需要遵循一個原則：先將這個元素嘗試性地放在已經存在的節點中，如果要存放的節點是2節點，那么插入后會變成3節點，如果要存放的節點是3節點，那么插入后會變成4節點（臨時）。然后，我們對可能生成的臨時4節點進行分裂處理，使得臨時4節點消失。

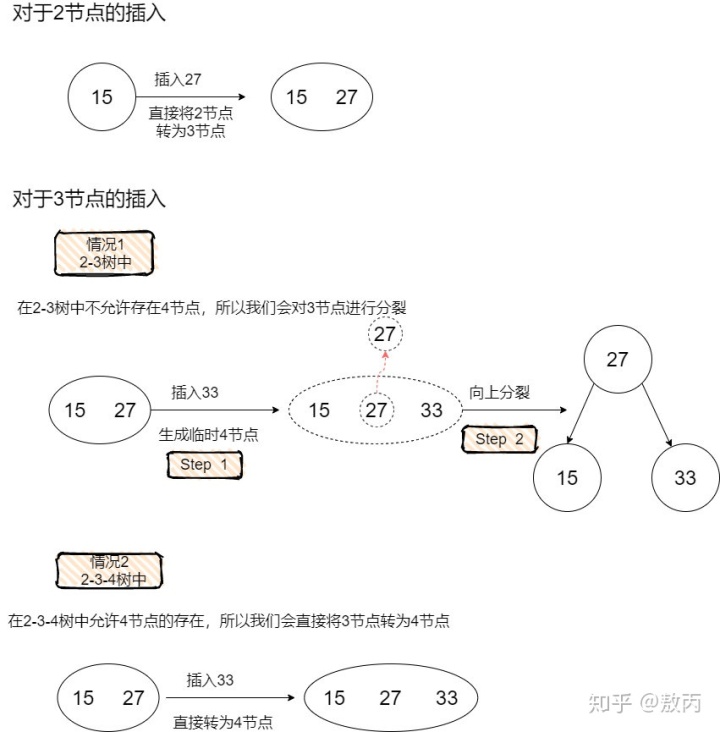
如果需要在2-3-4樹中向4節點內插入元素，那么會引發如下圖所示的分裂過程

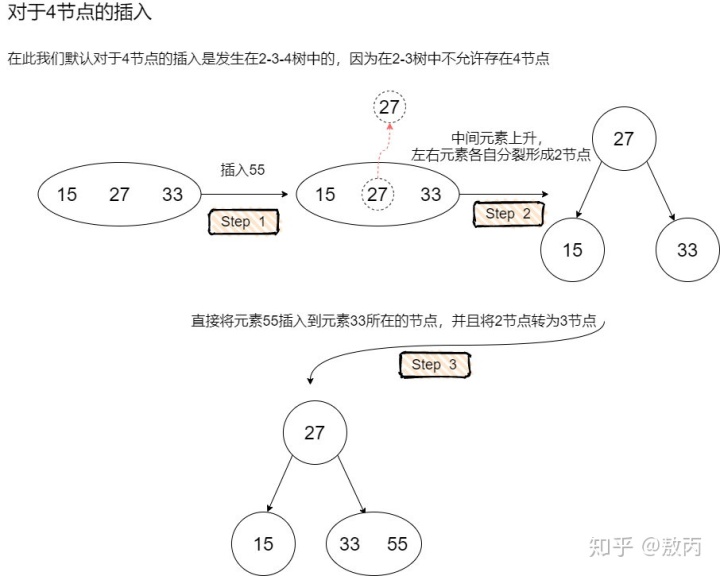
事實上，這正對應了紅黑樹在插入的時候一定會把待插入節點涂成紅色，因為紅色節點的意義是與父節點進行關聯，形成概念模型2-3樹中的3節點或者臨時4節點。
而紅黑樹之所以需要在插入后進行調整，正是因為可能存在著概念模型中的臨時4節點（反應在紅黑樹中是雙紅的情況）。
試想在2-3樹中如果待插入節點是個2節點，那么反應在紅黑樹中，不正好對應著黑色父節點嗎，在黑色父節點下面增加一個紅色兒子，確實不會違背紅黑樹的任何規則，這也對應著我們向2-3樹中的2節點插入一個元素，只需要簡單的把2節點變成3節點。
接下來讓我們來看一下對于2-3樹的刪除。對于2-3樹的刪除我們主要要考慮待刪除元素在2節點這種情況，因為如果待刪除元素在3節點，那么可以直接將這個元素刪除，而不會破壞2-3樹的任何性質（刪除這個元素不會引起高度的變化）。
當待刪除元素在2節點的時候，由于刪除這個元素會導致2節點失去自己唯一的元素，引發2節點自身的刪除，會使得樹中某條路徑的高度發生變化，樹變得不平衡。
因此我們有兩種方案去解決這個問題：

• 第一種方案，先刪除這個2節點，然后對樹進行平衡調整。
• 第二種方案，我們想辦法讓這個被刪除的元素不可能出現在2節點中。

本文選擇第二種方案，我們在搜索到這個節點的路徑中，不斷地判斷當前節點是否為2節點，如果是，就從它的兄弟節點或者它的父節點借一個元素，使得當前節點由2節點成為一個3節點或者一個臨時4節點（視具體情況而定，在后面的紅黑樹部分會詳細介紹）。
這種操作會產生一種結果：除非當前節點是根節點，否則當前節點的父節點一定是一個非2節點（因為搜索的路徑是自上而下，父節點已經進行過了這種操作，所以不可能是2節點），那么我們可以保證到達葉子節點的時候，也能順利的從父節點或者兄弟節點處借到元素，使得自己成為非2節點。從而能夠直接刪除某個元素（現在這個元素不在2節點中了）。

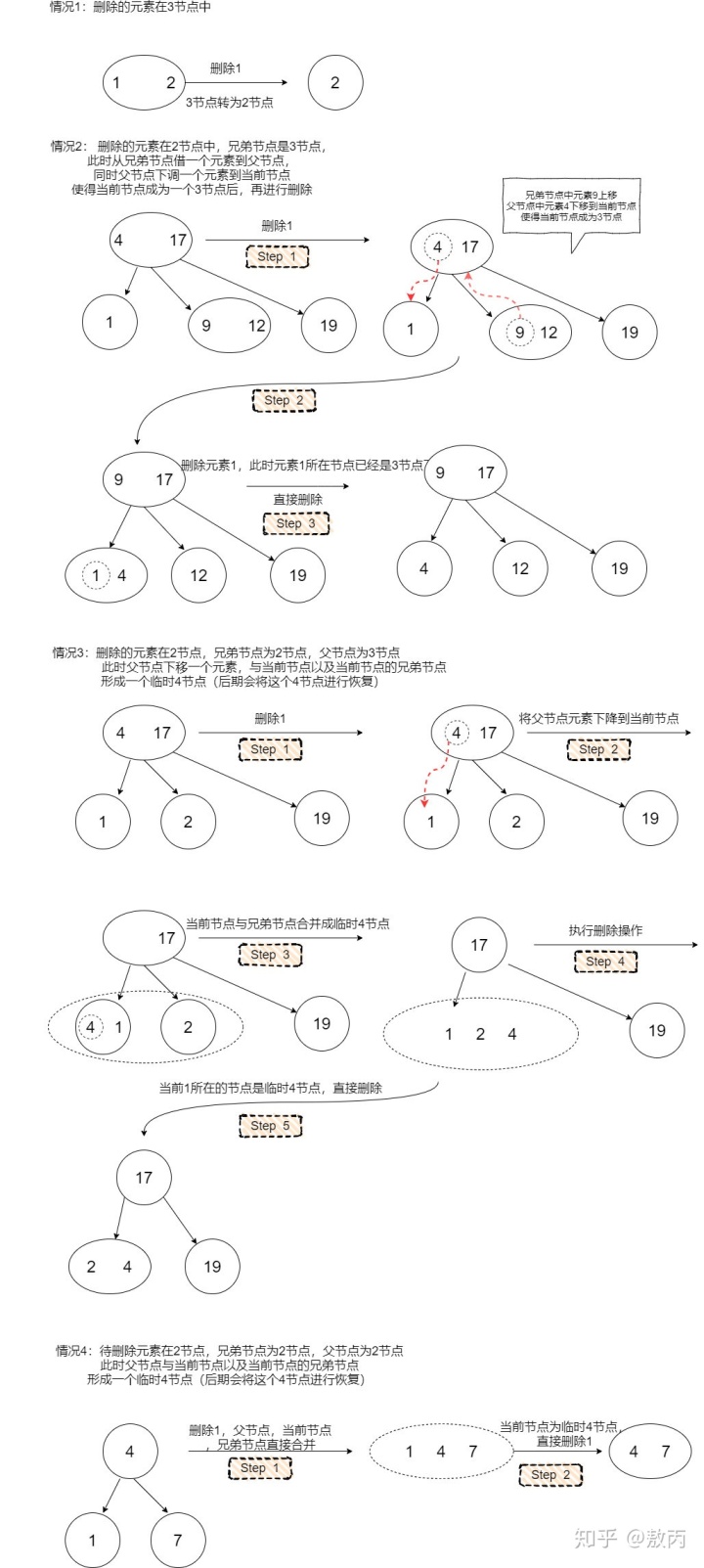
再看紅黑樹

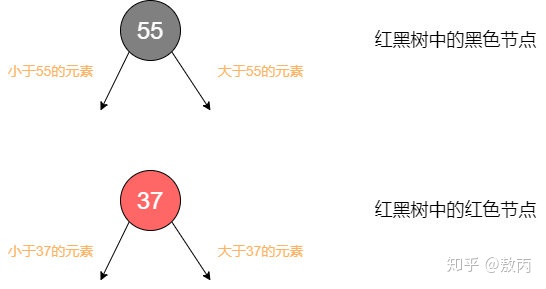
來看它的五條定義：1.節點顏色有紅色和黑色
【2-3樹到紅黑樹的轉化已經解釋過】2.根節點必為黑色
【2-3樹中如果根節點為2節點，那么它本來就對應紅黑樹中黑節點；如果根節點為3節點，也可以用黑色節點表示較大的那個元素，然后較小的元素作為左傾紅節點存在于紅黑樹中】3.所有葉子節點都是黑色
【此處提到的葉子其實是空鏈接，因篇幅問題不便全部畫出】
####4.任意節點到葉子節點經過的黑色節點數目相同
【紅黑樹中的紅節點是和黑色父節點綁定的，在2-3樹中本來就是同一層的，只有黑色節點才會在2-3樹中真正貢獻高度，由于2-3樹的任一節點到空鏈接距離相同，因此反應在紅黑樹中就是黑色完美平衡】5.不會有連續的紅色節點
【2-3樹中本來就規定沒有4節點，2-3-4樹中雖然有4節點，但是要求在紅黑樹中體現為一黑色節點帶兩紅色兒子，分布左右，所以也不會有連續紅節點】
相信在你的視角中，紅黑樹已經不再是這五條僵硬的定義了，它背后正浮現著一顆2-3樹概念模型。雖然你已經有了這樣的認識，但是紅黑樹作為真正的實現模型，我們還是要回到這個實現本身來探究它的一系列操作。在開始前，我準備了兩個基礎知識，希望能幫助到你。1.作為二叉查找樹
二叉查找樹的節點有一個元素X和兩個指針域，左指針指向小于X的元素，右指針指向大于X的元素。
假設我們的插入序列是1~10，那么這顆樹會演變成只有右鏈接的形式，樹高會增加到10層，這個時候已經不具備O(LogN)的查找時間復雜度，因為這顆樹退化成了鏈表。
因此對二叉樹進行平衡調整是很重要的一個環節，無論是AVL還是紅黑樹，它們本質上都是希望盡可能保證這顆二叉查找樹中的元素盡量均衡的分布在樹的兩側。
當我們向一顆二叉查找樹中插入一個元素Y的時候，我們會一直與樹中的節點進行大小比較，如果Y小于當前元素，就往左走，如果Y大于當前元素，就往右走，直到達到葉子節點，這個時候我們可以把Y插入這顆二叉查找樹了。
由于這次的插入動作，整棵樹可能會發生一些不平衡，因此我們需要在插入后進行一次平衡調整，使得整棵樹恢復到平衡的狀態（具體如何調整，要看樹是AVL還是紅黑樹亦或是其他的平衡樹）。
二叉查找樹的刪除是一個很有意思的問題，不同于插入的是，待刪除的元素并不能保證一定出現在樹中的葉子節點。這將帶來一個棘手的情景，即我們需要從樹的中間部分取走一個元素，而且在取走后還需要經過調整來使得整顆樹滿足平衡的性質。從樹的中間部分直接取走一個節點的場景實在是太多，也牽扯到了太多相關的節點，這種操作很難實現。
好在有人提出了一個觀點，我們對查找樹中一個節點的刪除，其實可以不必真的改動這個節點的位置。由于查找樹的特殊性質，將某個元素節點刪除后，它有兩個最佳替代者，分別是有序序列中的前驅元素和后繼元素。
我們還是以一個包含元素1~10的二叉查找樹為例，如果我們希望刪除5所在的節點，那么讓4或者6替代它的位置都是可行的。作為前驅元素的4，會存放在5所在節點的左子樹的最右側；作為后繼元素的6，會存放在5所在節點的右子樹的最左側。
關于這個結論，大家只需稍加思索便可以明白。
現在我們又讓問題簡化了，也就是說，刪除某個節點的時候，我們先找到它的前驅元素或者后繼元素（隨便選一個），將它的前驅元素直接填到待刪除的節點，然后再把它的前驅元素或者后繼元素刪除。
這個時候問題就轉化成了在二叉查找樹中刪除一個沒有左子樹的節點（或者是一個沒有右子樹的節點），我們只需要將這個節點刪除再進行對應的平衡調整即可（雖然還是需要調平，但是比直接在樹中層刪除一個同時具備左右兒子的節點要容易很多）。
注意，此處并沒有強調是針對紅黑樹的操作，因為紅黑樹和AVL都是二叉查找樹，它們都適用這個方法。介紹一下樹的旋轉
為了調平一顆二叉樹，使得其左右節點數目分布均勻，通常會選擇旋轉的手段。你可以把一顆二叉樹某節點的左右子樹想象成天平上待稱量的物品，如果哪邊重了，我們就從重的那邊拿出一部分，加到輕的那邊，以此保持相對的平均。
在二叉樹中這種調整的操作就是旋轉，下面給出了兩個示例，希望大家能夠仔細探究，旋轉是二叉樹調平的精髓。
介紹一下樹的旋轉

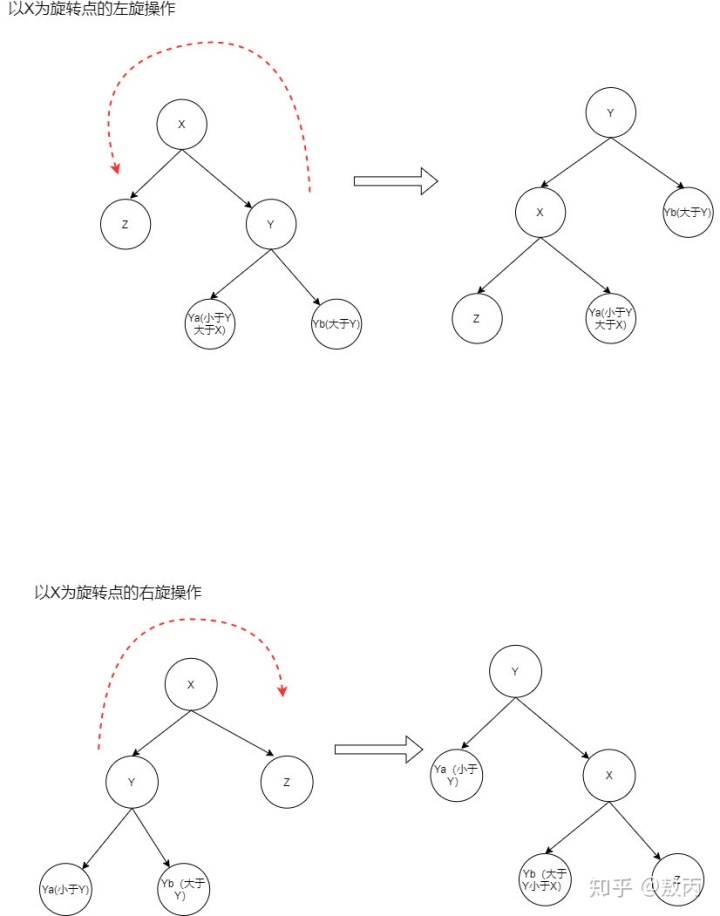
理解了這些之后，再去看紅黑樹的插入刪除，就能夠理解旋轉和染色背后的意義了。 我們選擇算法4中的左傾紅黑樹作演示：首先看插入

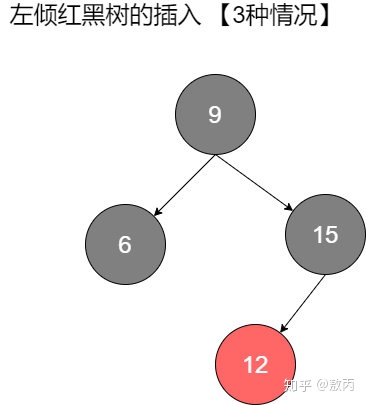
如圖所示，對于左傾紅黑樹的插入一共有三種可能的情況。

• 第一種，待插入元素比黑父大，插在了黑父的右邊，而黑父左邊是紅色兒子。這種情況會導致在紅黑樹中出現右傾紅節點。
  注意，這種情況對應著2-3樹中出現了臨時4節點，我們在2-3樹中的處理是將這個臨時4節點分裂，左右元素各自形成一個2節點，中間元素上升到上層跟父節點結合。所以，我們在紅黑樹中的動作是，將原本紅色的左右兒子染黑（左右分裂），將黑父染紅（等待上升結合）。

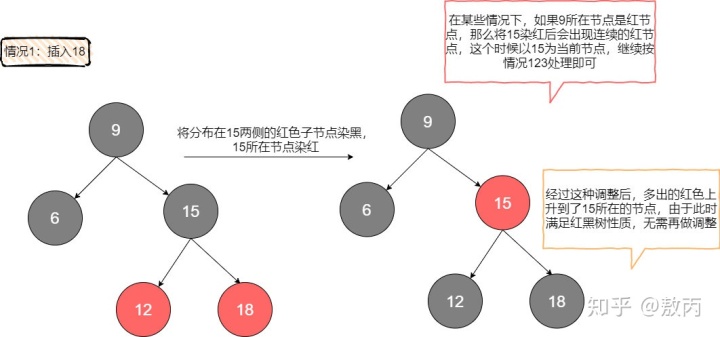
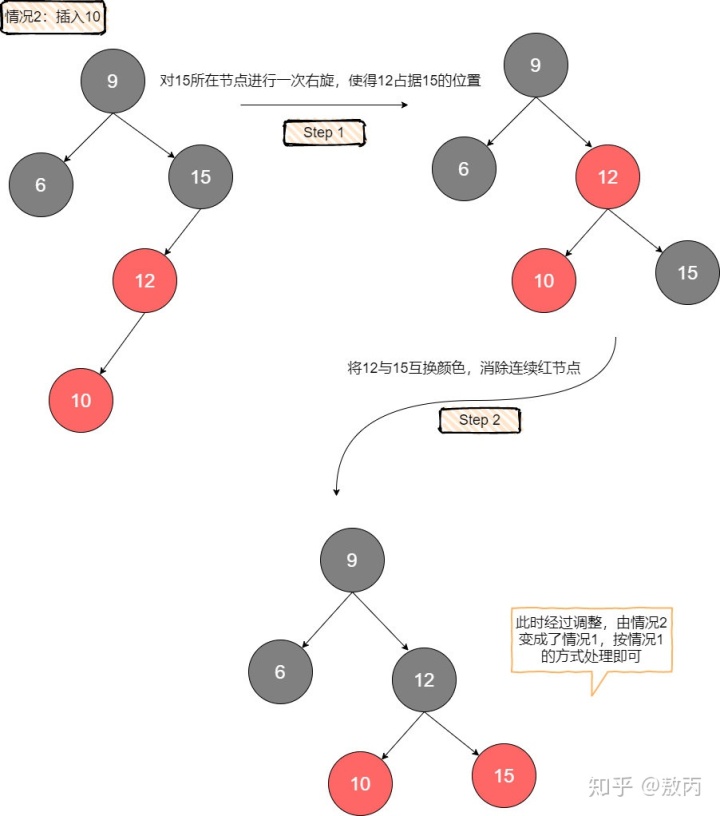
• 第二種情況，待插入元素比紅父小，且紅父自身就是左傾。聽起來有點繞，看圖就會明白，其實就是說紅父和待插入元素同時靠在了左邊，形成了連續的紅節點。
  這種情況我們需要用兩步來調整。由于我們插入的是紅色節點，其實不會破壞黑色完美平衡，所以要注意的是在旋轉和染色的過程種繼續保持這種完美黑色平衡。
  首先對紅父的父親進行一次右旋，這次右旋不會破壞黑色平衡，但是也沒有解決連續紅色的問題。
  接下來將12所在節點與15所在節點交換顏色，這樣的目的是為了消除連續紅色，并且這個操作依舊維持了黑色平衡。現在我們已經得到了情況1的場景，直接按情況1處理即可。

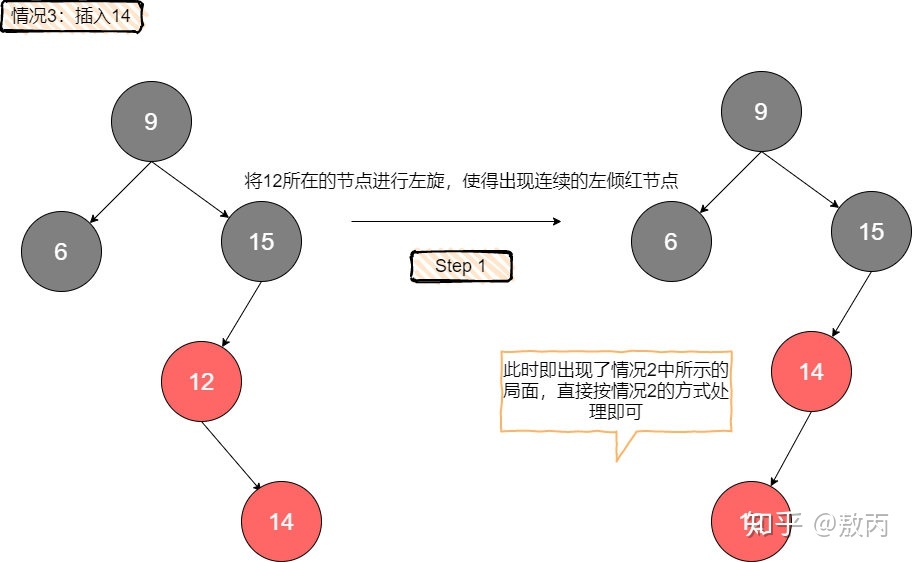
• 第三種情況，待插入元素比紅父大，且紅父自身就是左傾。
  也就是說插入的這個節點形成了一個右傾的紅色節點，對右傾的處理很簡單，將紅父進行一次左旋，就能使得右傾紅節點變為左傾，現在出現了連續的左傾紅節點，直接按情況2處理即可。

在插入時，可以體會到左傾紅黑樹對于左傾的限制帶來的好處，因為在原樹符合紅黑樹定義的情況下，如果父親是紅的，那么它一定左傾，同時也不用考慮可能存在的右傾兄弟（如果有，那說明原樹不滿足紅黑樹定義）。
這種限制消除了很多需要考慮的場景，讓插入變得更加簡單。左傾紅黑樹的刪除
左傾紅黑樹的刪除需要借鑒上文中提到的二叉查找樹通用的刪除策略，當我們要刪除某個節點的時候選擇它的前驅節點或者后繼節點元素來替代它，轉而刪除它的前驅/后繼節點。
在這個例子中，我選擇用后繼節點來替代被刪除節點。
假設我們需要刪除的節點它的右子樹如圖所示，那么對該節點的刪除實際上轉為了對2的刪除。
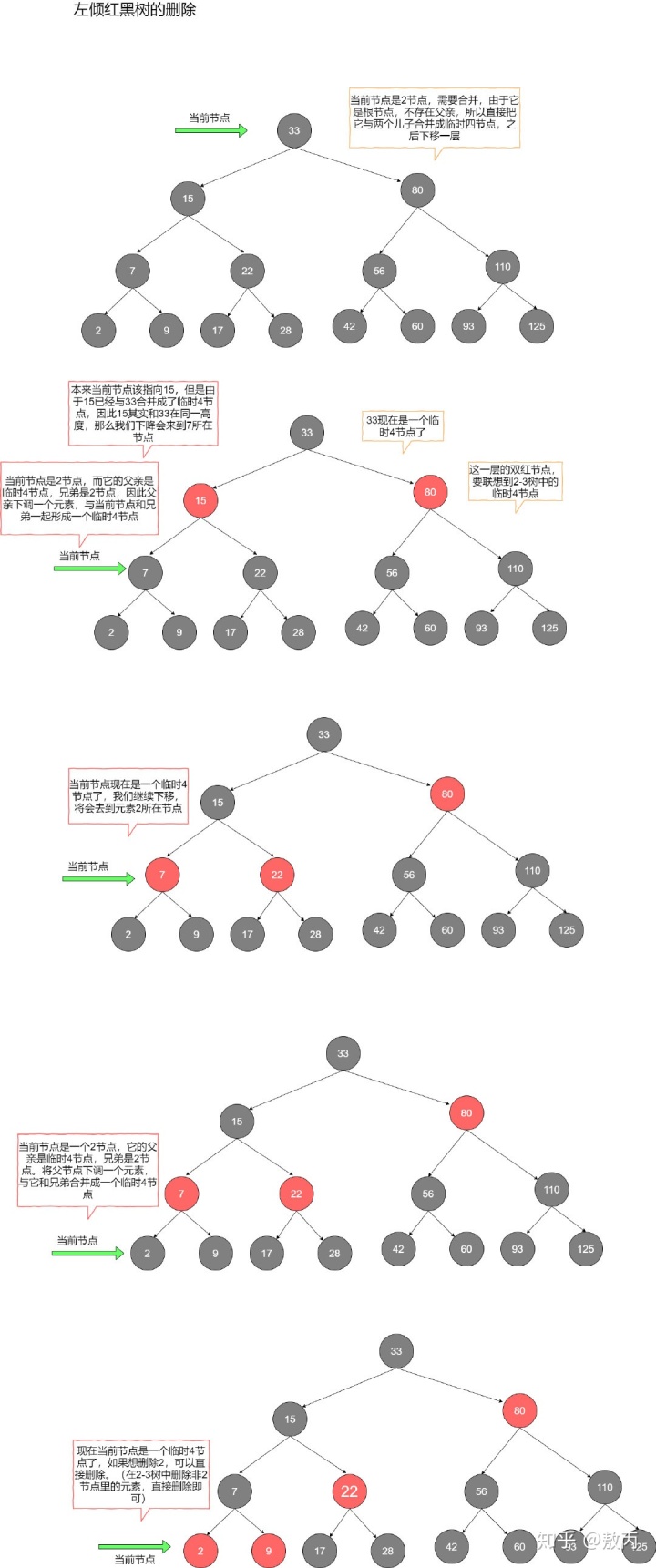
我們從當前的根節點出發，利于2-3樹中預合并的策略逐層對紅黑樹進行調整。具體的做法是，每次都保證當前的節點是2-3樹中的非2節點，如果當前節點已經是非2節點，那么直接跳過；如果當前節點是2節點，那么根據兄弟節點的狀況來進行調整：

• 如果兄弟是2節點，那么從父節點借一個元素給當前節點，然后與兄弟節點一起形成一個臨時4節點。
• 如果兄弟是非2節點，那么兄弟上升一個元素到父節點，同時父節點下降一個元素到當前節點，使得當前節點成為一個3節點。

這樣的策略能夠保證最后走到待刪除節點的時候，它一定是一個非2節點，我們可以直接將其元素刪除。

接下來要考慮的是修復工作，由于紅黑樹定義的限制，我們在調整的過程中出現了一些本不該存在的紅色右傾節點（因為生成了概念模型中的臨時4節點），于是我們順著搜索的方向向上回溯，如果遇到當前節點具備右傾的紅色兒子，那么對當前節點進行一次左旋，這時原本的右兒子會來到當前節點的位置，然后將右兒子與當前節點交換顏色，我們就將右傾紅節點修復成了左傾紅節點，同時我們并沒有破壞黑色節點的平衡。

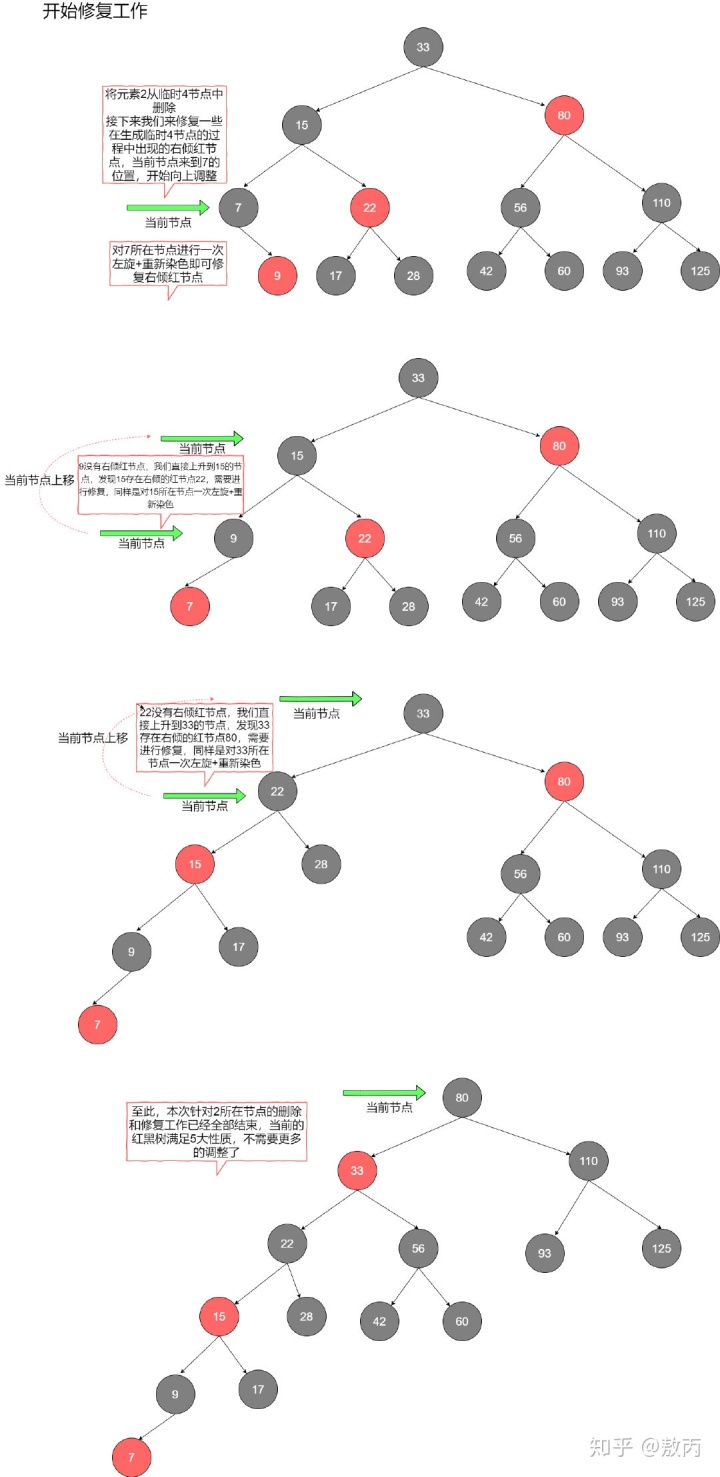
右傾轉左傾是一個很基本的操作，我們以35，44為例，你既可以將35作為黑節點，44作為右傾紅色兒子；也可以將44作為黑節點，35作為左傾紅兒子。事實上我們對于右傾的修復就是換了一種樹形而已。一路回溯到當前根節點，直至路徑中不再包含任何的紅色右傾節點，至此修復工作全部完成。總結
這篇文章的目的旨在從概念模型2-3樹出發介紹一顆紅黑樹的前世今生。希望大家能夠跳出枯燥的五條定義，更加本質地認識紅黑樹中的各種操作來源。
雖然本文只是介紹了相對簡單的左傾紅黑樹，但是如果能夠將左傾紅黑樹認識的很清楚，那么普通紅黑樹也只是多了一些情況而已。
對于還有精力閱讀算法導論的讀者，我給出一點自己的經驗：

• 插入階段與左傾紅黑樹比較相似
• 配圖中的部分節點標識不太清楚，要反復對照原文閱讀
• 刪除階段，算法導論中將刪除黑節點X帶來的黑色平衡破壞解釋為，給X的子節點添上額外的一層黑色，讓X的子節點變為【雙重黑】或者【既黑又紅】的。
  我其實不太接受這種解釋，經過考慮，我認為其實這個表達可以更直接一點：既然刪除了某個黑色節點，那么必然會破壞以這個黑色節點為路徑上的黑色平衡，表現為路徑中缺少一個黑。
  如果你仔細研究算法導論中的四個刪除場景，會發現它們在做的事情其實都是從兄弟節點的路徑想辦法移動一個黑色節點過來。
  因此，如果實在無法理解【雙重黑】，【既黑又紅】，那么直接按照“某條路徑欠黑，所以要想辦法補充一個黑色節點”這個思路來思考吧！
• 還是刪除階段，四個刪除場景該如何記憶？我們假設刪除的是某個左傾節點，其實決定場景變化的就是三個因素：這個節點的兄弟顏色；兄弟的左右兒子的顏色；這個節點的父節點的顏色。這樣子粗略估計有2x2x2x2共16種情況。實際上會少很多，我們從兄弟的顏色入手。請注意如果兄弟是紅色，那么當前節點的父親和兄弟的兒子其實都是黑色。而當兄弟是黑色的時候，我們只需要滿足兄弟的右兒子是紅色，就能通過一次調整來實現平衡（具體請參照算法導論）。
  另外提醒注意的是，一定要想好記憶的順序。算法導論中的刪除調平4種情況中，只有情況4是絕對終態，也就是說到達了這種狀態后只需要一次調整絕對能達到平衡。所以我們的出發點一定是從這種狀態開始，對于另外幾種情況，我們要想的不是怎么去達到最終平衡，而是怎么能讓它一步一步轉為情況4。這樣子你的思路就會清晰很多，記憶的壓力也會減小。如果細心的話，你可以回想一下本文是按照怎樣的順序介紹左傾紅黑樹的插入的，為什么是這樣的順序？
• 一個數據結構可視化網站，它的紅黑樹是基于2-3-4樹的，跟算法導論中基本一樣（除了刪除時候對前驅/后繼節點的選擇），可以用它當做檢驗。https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

寫在最后
最后，如果你被問到紅黑樹，也許你可以試著反問面試官一個問題：“您應該知道紅黑樹的五條定義，如果我構造一顆只有黑色節點的紅黑樹，這樣子可行嗎？因為這樣子沒有破壞任何一條紅黑樹的規則。”
如果他回答可行。
繼續問：“那么請問紅黑樹中要紅節點干什么呢？紅節點的真實意義是什么呢？”
你們的故事就開始了，而我和你的算法故事也才剛開始。