目錄
- 概括
- Sparse PCA Formulation
- 非常普遍的問題
- Optimality Conditions
- Eigenvalue Bounds
- 算法
- 代碼

概括
這篇論文,不像以往的那些論文,構造優化問題,然后再求解這個問題(一般都是凸化)。而是,直接選擇某些特征,自然,不是瞎選的,論文給了一些理論支撐。但是,說實話,對于這個算法,我不敢茍同,我覺得好麻煩的。
Sparse PCA Formulation
非常普遍的問題
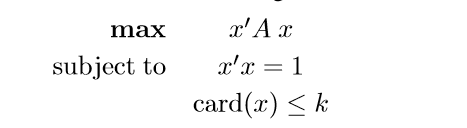
Optimality Conditions
這一小節,論文給出了,上述問題在取得最優的情況下應該符合條件。
條件1
如果\(x^{*} \quad \mathbf{Card}(x^{*})=k\)是上述問題的最優解,那么\(z^{*}\)(由\(x^{*}\)非零元組成)是子舉證\(A_k^{*}\)(\(x^{*}\)非零元所在位置,\(A\)的\(k\)行\(k\)列)的主特征向量。
這個條件是顯然的。
條件2
感覺和上面也沒差啊。
Eigenvalue Bounds
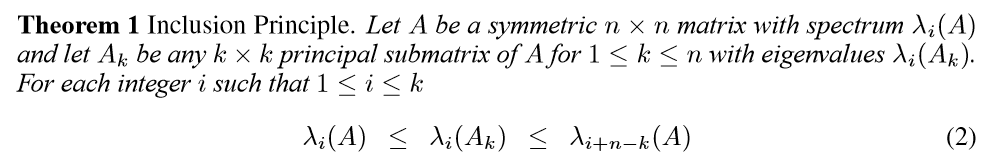
這個定理,可以由一個事實導出:
\(A \in \mathbb{R}^{n\times n}\)為一對稱矩陣,\(\lambda_i\)為其特征值,且降序排列。
\(A_{n-1}\)為\(A\)的任意\(n-1\)級主子式,\(\delta_i \quad i=1,2,\ldots,n-1\)為其特征值,那么有下面分隔:
\(\lambda_1 \leq \delta_1 \leq \lambda_2 \leq \ldots \leq \delta_{n-1} \leq \lambda_n\)
根據這個事實,再用歸納法就可以推出上面式子。
分隔定理的證明(《代數特征值問題》p98)
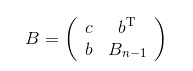
存在正交變換\(Q\),使得\(Q^{\mathrm{T}}BQ\)右下角變為對角陣。若正交矩陣\(S\)使得\(S^{\mathrm{T}}B_{n-1}S\)為對角陣,那么,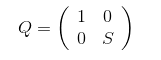
且右下角矩陣的特征值并沒有變化。
令: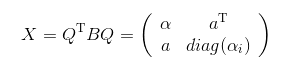
設\(a\)只有\(s\)個成分不為0,若\(a_j=0\),那么\(\alpha_j\)就是\(X\)的特征值。
經過一個適當的置換矩陣\(P\)變換,我們可以得到:
(注意,下面的\(b\)和上面的\(b\)不是一個\(b\),只是為了與書上的符號相一致)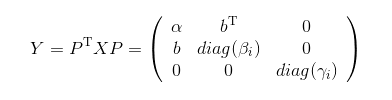
那么只需要考慮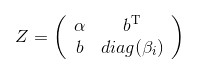
的特征值就行了,因為\(\gamma_i\)是矩陣\(A\)和\(A_{n-1}\)所共有的。
考慮\(Z\)的特征多項式:
\((\alpha-\lambda)\mathop{\prod}\limits_{i=1}^{s}(\beta_i-\lambda)- \mathop{\sum}\limits_{j=1}^{s}b_j^2\mathop{\prod}\limits_{i \neq j}(\beta_i-\lambda)=0\)
假定\(\beta_i\)中只有\(t\)個不同的值,不失一般性,可令它們為\(\beta_1,\beta_2,\ldots,\beta_t\),
且重數為\(r_1,r_2,\ldots,r_s \quad \mathop{\sum}\limits_{i}r_i=s\)
等式左端有因子:
\(\mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i-1}\)
因此,\(\beta_i\)為\(Z\)的特征值,重數為\(r_i-1\)
等式除以\(\mathop{\sum}\limits_{i=1}^{t}(\beta_i-\lambda)^{r_i}\)可得:
\(0=(\alpha-\lambda)- \mathop{\sum}\limits_{i=1}^{t}c_i^2(\beta_i-\lambda)^{-1} =a-f(\lambda)\)
\(Z\)的剩余的特征值是\(a-f(\lambda)=0\)的根。
根據正負的特點,和連續函數(實質上是分段的)根的存在性定理,可以知道
\(a-f(\lambda)\)的\(t+1\)個根\(\delta_i\)滿足:
\(\delta_1>\beta_1>\delta_2>\ldots>\beta_t>\delta_{t+1}\)
這樣所有根的序列就得到了,就是我們要證的。整理一下可以得到,
除了剛剛講的\(t+1\)個根,
還有\(s-t\)個\(\beta_i\)相同的特征值,以及
\(n-s-1\)個\(\gamma_i\).
另外一個性質
這個性質不想去弄明白了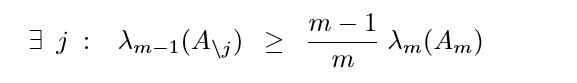
算法
我的理解這樣的:
step1.選第一個特征,就是對角元最大的那個
step2.在第一個的基礎上,再選一個,這次會形成一個\(2\times2\)的子矩陣,所以,需要選擇令這個矩陣首特征值最大的第二個特征。
step3.反復進行,直到k?
這是前向的,還有對應的后向的,一個個減。論文推薦是,倆種都進行,然后挑二者中比較好的一個。
未免太復雜了些?
代碼
只寫了前向的代碼:
import numpy as np
def You_eig_value(C): #冪法 只輸出特征值d = C.shape[1]x1 = np.random.random(d)while True:x2 = C @ x1x2 = x2 / np.sqrt(x2 @ x2)if np.sum(np.abs(x2-x1)) < 0.0001:breakelse:x1 = x2return x1 @ C @ x1def forward(C):n = C.shape[0]label1 = set(range(n))label = [np.argsort(np.diag(C))[-1]]label1 -= set(label)count = 0while len(label1) > 0:count += 1maxvalue = 0maxi = -1for i in label1:value = You_eig_value(C[label+[i],:][:,label + [i]])if value > maxvalue:maxvalue = valuemaxi = ilabel.append(maxi)label1 -= {maxi}return labelf = open('C:/Users/biiig/Desktop/pitprops.txt')
C = []
for i in f:C.append(list(map(float, i.split())))
f.close()
C = np.array(C)
forward(C) # [12, 6, 5, 9, 1, 0, 8, 7, 3, 2, 11, 4, 10]






)




 報錯1225)

)




)