1.何為KMP算法

? ? ?KMP算法是由Knuth、Morris和Pratt三位學者發明的，所以取了三位學者名字的首字母，叫作KMP算法。

2.KMP的用處

? ? ?KMP主要用于字符串匹配的問題，主要思想是當出現字符串不匹配時，我們可以知道一部分之前已經匹配過的的文本內容，利用這些信息從而避免從頭再開始匹配。

? ? ?但是如何才能知道之前已經匹配過的內容呢？這是KMP算法的核心，也是KMP算法里面的next數組的用處。

3.最長相等前后綴

? ? ?一個字符串的前綴是指不包含最后一個字符的所有以第一個字符開頭的連續字串

? ? ?后綴是指不包含第一個字符的所有以最后一個字符結尾的連續子串

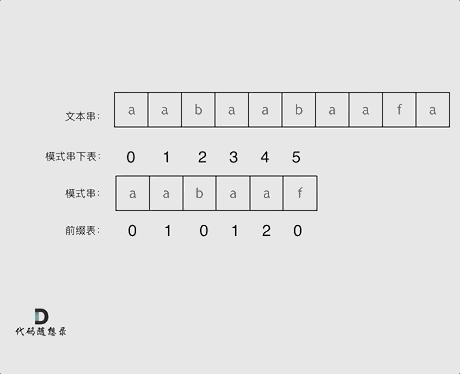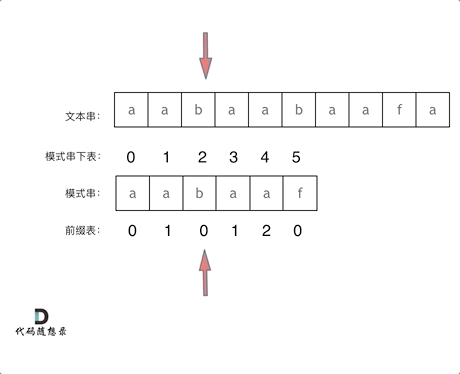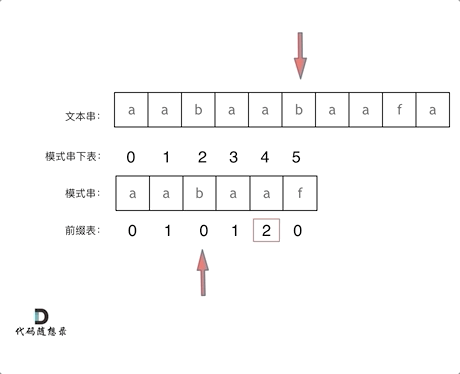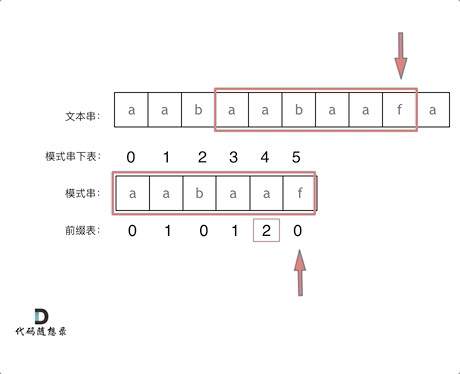
? ? ?前綴表也就是next數組要求的是最長相等前后綴的長度，例如a的最長相等前后綴為0，aaa得到最長相等前后綴為2，aaba的最長相等前后綴為1。

4.next數組(前綴表)

? ? ?KMP的核心就是next數組，當模板串和主串不匹配時，next數組是用來讓模板串知道應該從哪里再開始匹配。

? ? ?next數組記錄下標i之前(包括i)的字符串中，有多大長度的相等前后綴。

? ? ?這里借用了代碼隨想錄的圖片

? ? ?比如我們要在文本串aabaabaafa中尋找模板串aabaaf，在b和f之前發現匹配不了，如果用暴力算法，就要從頭開始匹配，文本串和模板串都需要進行回退，時間復雜度是很高的，但如果我們使用KMP算法，next數組記錄了f之前有多大長度的相等前后綴，也就是我們知道了之前匹配過的內容，就會從上次已經匹配的內容開始匹配，這里為什么能這樣呢？我是這樣理解的：

? ? ?文本串: aabaabaafa ?用i遍歷

? ? ?模板串：aabaaf ? ? ?用j遍歷

? ? ?在b和f時不相同了，這時候我們不想再匹配我們已經匹配過的，也就是說我們不想i回退，而是一直向前走，那我們就要j進行回退，回退到什么位置呢，前面已經匹配到了，說明已經匹配過的文本串aabaa中含有模板串一部分內容，又因為前后綴有相等的部分。所以我們回退到前后綴相等的前綴位置，因為和文本串是相同的，所以aabaa的后綴aa和文本串的aabaa的后綴aa是相等的，又有aabaa的前綴aa和后綴aa是相等前后綴，所以前綴aa和文本串aabaa的后綴aa相等，我們回退到aabaa的b即可避免再次匹配aabaa的前綴aa，這樣也可以保證模板串aabaa的前綴aa是已經匹配過的。

? ? ? f之前這部分的字符串（也就是字符串aabaa）的最長相等前后綴是aa ，因為找到了最長相等的前后綴，匹配失敗的位置是后綴的后面，那么我們找到與其相同的前綴的后面重新匹配就可以了。

5.如何計算next數組

?例如a a b a a f下標0 1 2 3 4 5next 0 1 0 1 2 0

? ? ?當下標為0時，長度為前1個字符的字串a，最長相等前后綴的長度為0

? ? ?當下標為1時，長度為前2個字符的字串aa，最長相等前后綴的長度為1

? ? ?依次類比，可以得到next數組，也就是前綴表

? ? ?可以看出模板串和next數組對應位置的數字表示的是下標i之前(包括i)的字符串中，有多大長度的最長相等前后綴。

? ? ? 當我們找到不匹配的位置時，就要看它前一個字符的next數組的值是多少，因為我們要找前面字符串的最長相等前后綴，所以要看前一位的next數組的值，前一個字符的next數組值為2，所以我們把下標j移動到2的位置繼續匹配，這樣就可以匹配到了。

6.next數組實現

? ? ?主要是處理前后綴相等和不相等的情況，我們首先定義一個getNext函數來構造next數組，參數為指向next數組的指針，和一個字符串

void getNext(int* next,string& s)

? ? ?接著我們對其進行初始化，定義兩個指針i和j，j指向前綴末尾，i指向后綴末尾，對next數組進行初始化賦值

int j=0;
next[0]=j;

? ? ?next[i]表示i(包括i)之前最長相等的前后綴長度，就是j，所以初始化next[0]=j

6.1前后綴不相同

? ? ?j=0，所以我們從i=1開始，遍歷文本串，就像這樣

for(int i=0;i<s.size();i++)

? ? ? j首先要保證是大于0的，因為下面j要回退，然后就是s[i]和s[j]的比較，如果s[i]和s[j]不相同，j就要找前一位對應的回退位置，因為這里j之前的前綴已經和i的后綴不相等了，所以我們就要j進行回退。

while(j>=0&&s[i]!=s[j])
{j=next[j-1];
}

?6.2前后綴相同

? ? ?如果是s[i]和s[j]相同，這時候只要同時移動i和j，這時候找到了相同的前后綴，我們要把j的值賦值給next[i]，因為next[i]記錄相同前后綴的長度

if(s[i]==s[j])
{j++;
}
next[i]=j;

? ? ? 完整代碼如下：?

void getNext(int* next, const string& s) 
{int j = 0;next[0] = 0;for(int i = 1; i < s.size(); i++) {while (j > 0 && s[i] != s[j]){ j = next[j - 1]; }if (s[i] == s[j]){j++;}next[i] = j;}
}

7.例題? ??

?

  void getNext(int* next,const string& s){int j=0;next[0]=0;for(int i=1;i<s.size();i++){while(j>0&&s[i]!=s[j]){j=next[j-1];}if(s[i]==s[j]){j++;}next[i]=j;}}int strStr(string haystack,string needle){if(needle.size()==0){return 0;}int next[needle.size()];getNext(next,needle);int j=0;for(int i=0;i<haystack.size();i++){while(j>0&&haystack[i]!=needle[j]){j=next[j-1];}if(haystack[i]==needle[j]){j++;}if(j==needle.size()){return (i-needle.size()+1) ;}}return -1;}

? ? ?這道題很明顯是字符串匹配的問題，所以我們使用KMP算法，首先是next數組的構建，這是模板，直接寫就行，然后就是模板串和文本串的匹配，如果不相同，那j就回退到next[j-1]，如果相同，j就直接向后移動即可，當j和模板串的長度相等時，此時i一定是大于等于模板串的長度的，因為i之前的文本串是包含模板串的，所以我們用i-模板串的長度+1就是第一個匹配項的下標了。