4. 稀疏自編碼
假設我們只有一個沒有類別標簽的訓練樣本集合{x(1),x(2)...},一個自編碼神經網絡就是一種非監督學習算法,它使用BP算法,并將目標值設為: y(i)=x(i)。
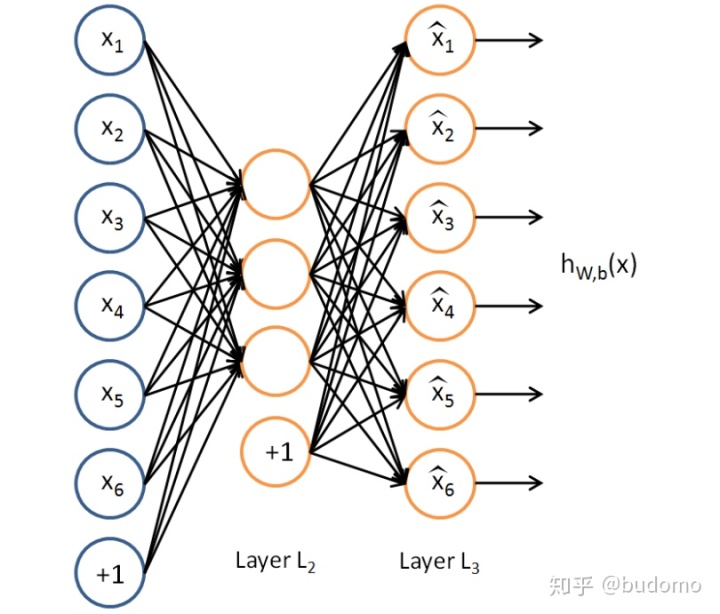
我們的目標是希望得到hW,b(X)≈x。用aj(2)(x)表示輸入向量x對隱藏層單元j的激活值。則j的平均激活值:
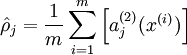
為了達到稀疏性,也即用最少(最稀疏)的隱藏單元來表示輸入層的特征(也即,對每一個輸入X, 其特征表示是稀疏的),我們希望所有隱藏層單元平均激活值接近于0.于是應用KL距離:
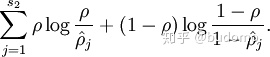
其中為了方便書寫:
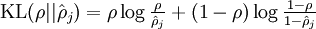
其中,
這樣,神經網絡整體代價函數就可以表示為:
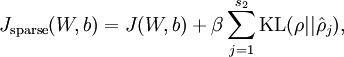
,其中J(W,b)是BP自身的損失函數,預測損失+參數L2正則(減小權重的幅度,防止過度擬合)
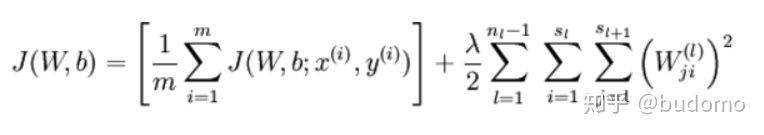
這樣,一個稀疏自編碼器就完成了。
代碼:
Sparse自編碼 Autoencoder, 基本按照標準公式實現##### 設置網絡參數 #####
p = 0.05 # 使大部分神經元的激活值(所有神經元的激活值的平均值)接近這個p值
beta = 3 # 控制KL散度所占的比重input_dim = 784
encoding_dim = 64
lambda_val = 0.001 # J(W,b)自帶的對W進行的L2正則,weight decayepochs = 50
batch_size = 1024# 自定義正則項函數, 計算KL散度
def sparse_reg(activity_matrix):activity_matrix = K.softmax(activity_matrix, axis=0) # 把激活值先用softmax歸一化p_hat = K.mean(activity_matrix, axis=0) # 將第j個神經元在batch_size個輸入下所有的輸出激活值取平均print('p_hat=', p_hat)KLD = p*(K.log(p/p_hat))+(1-p)*(K.log((1-p)/(1-p_hat))) # 計算KL散度print('KLD=', KLD)return beta*K.sum(KLD) # 所有神經元的KL散度相加并乘以betainput_img = Input(shape=(input_dim,))h = Dense(encoding_dim,activation='relu',kernel_regularizer=regularizers.l2(lambda_val/2),activity_regularizer=sparse_reg)(input_img)r = Dense(input_dim, activation='sigmoid',kernel_regularizer=regularizers.l2(lambda_val/2),activity_regularizer=sparse_reg)(h)# sparse AE模型
autoencoder = Model(inputs=input_img, outputs=r)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
#輸出模型結構
print(autoencoder.summary())# 注意:輸出是干凈的X_train
history = autoencoder.fit(X_train, X_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(X_test, X_test))#編碼過程: 取出編碼部分
conv_encoder = Model(input_img, h)
#在測試集上進行編碼輸出,輸出圖形的編碼形式(64維度)
encoded_imgs = conv_encoder.predict(X_test)n = 10
plt.figure(figsize=(20, 8))
for i in range(n):ax = plt.subplot(1, n, i+1)plt.imshow(encoded_imgs[i].reshape(4, 16).T)plt.gray()ax.get_xaxis().set_visible(False)ax.get_yaxis().set_visible(False)
plt.show()#解碼過程:
#Predict on the test set
decoded_imgs = autoencoder.predict(X_test)生成的編碼圖像(64維)
變稀疏了嗎?

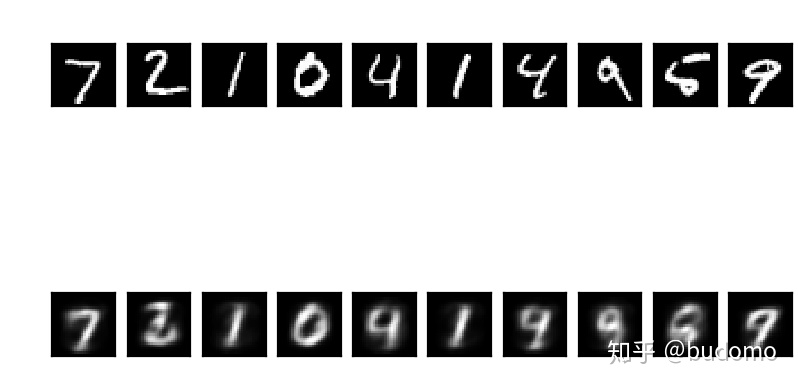
)










)



的操作)

![spark sql讀取hive底層_[大數據]spark sql讀寫Hive數據不一致](http://pic.xiahunao.cn/spark sql讀取hive底層_[大數據]spark sql讀寫Hive數據不一致)

