文章目錄
- 圖的認識
- 圖的概念
- 無向圖
- 有向圖
- 簡單圖
- 完全圖
- 子圖
- 連通、連通圖、連通分量
- 邊的權和網
- 加權圖
- 鄰接和關聯
- 路徑
- 簡單路徑、簡單回路
- 環
- 頂點的度、入度和出度
- 割點(關節點)
- 橋(割邊)
- 距離
- 有向樹
- 圖的表示
- 鄰接列表
- 鄰接矩陣
- 圖的遍歷
- 深度優先遍歷
- 廣度優先遍歷
- 生成樹
圖的認識
圖(Graph)是由頂點和連接頂點的邊構成的離散結構。一個圖就是一些頂點的集合,這些頂點通過一系列邊結對(連接)。頂點用圓圈表示,邊就是這些圓圈之間的連線。頂點之間通過邊連接。
注意:線性表可以是空表,樹可以是空樹,圖不可以是空圖,圖可以沒有邊,但是至少要有一個頂點。
圖是最靈活的數據結構之一,很多問題都可以使用圖模型進行建模求解。
樹可以說只是圖的特例,但樹比圖復雜很多
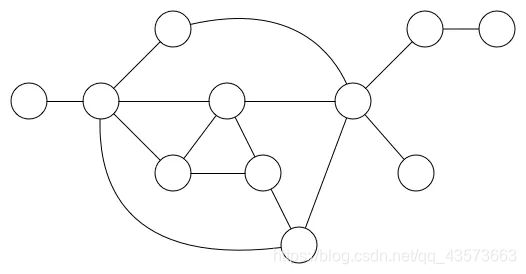
注意:頂點有時也稱為節點或者交點,邊有時也稱為鏈接。
圖有各種形狀和大小。邊可以有權重(weight),即每一條邊會被分配一個正數或者負數值。邊可以是有方向的。有方向的邊意味著是單方面的關系。從頂點 X 到 頂點 Y 的邊是將 X 聯向 Y,不是將 Y 聯向 X。
樹和鏈表,都可以被當成是樹,是一種更簡單的形式。他們都有頂點(節點)和邊(連接)。
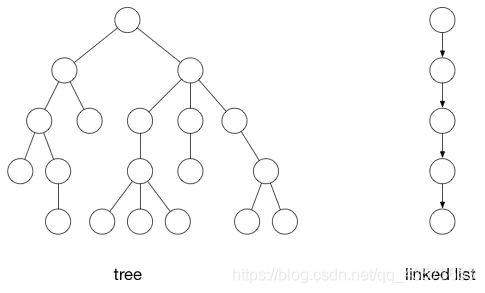
圖的概念
圖是由頂點集合以及頂點間的關系集合組成的一種數據結構。
由頂點 V 集和邊 E 集構成,因此圖可以表示成 Graph = (V,E)
V是頂點的有窮非空集合;E是頂點之間關系的有窮集合,也叫邊集合。
圖按照邊或弧的多少分稀疏圖和稠密圖
無向圖
無向圖:頂點對<x,y>是無序的。
無向邊:若頂點Vi到Vj之間的邊沒有方向,則稱這條邊為無向邊,用無序偶對(Vi,Vj)來表示
無向圖頂點的邊數叫做度。
無向圖中,頂點的度就是與頂點相關聯的邊的數目,沒有入度和出度。
如果圖中任意兩個頂點時間的邊都是無向邊,則稱該圖為無向圖:

上圖是無向圖,所以連接頂點A與D的邊,可以表示為無序對(A,D),也可以寫成(D,A)
對于如上無向圖來說,G=(V,{E}) 其中頂點集合V={A,B,C,D};邊集合E={(A,B),(B,C),(C,D),(D,A),(A,C)}
完全無向圖:若有n個頂點的無向圖有n(n-1)/2 條邊, 則此圖為完全無向圖。
有向圖
如果任意兩個頂點之間都存在邊叫完全圖,有向的叫有向圖。
有向圖:具有方向性,頂點 (u,v)之間的關系和頂點 (v,u)之間的關系不同,后者或許不存在。
有向圖:頂點對<x,y>是有序的;
有向邊:若從頂點Vi到Vj的邊有方向,則稱這條邊為有向邊,也稱為弧。
用有序偶<Vi,Vj>來表示,Vi稱為弧尾,Vj稱為弧頭。

連接頂點A到D的有向邊就是弧,A是弧尾,D是弧頭,<A,D>表示弧。注意不能寫成<D,A>。
對于如上有向圖來說,G=(V,{E})其中頂點集合V={A,B,C,D};弧集合E={<A,D>,<B,A>,<C,A>,<B,C>}
圖中頂點之間有鄰接點。有向圖頂點分為入度和出度。
簡單圖
若無重復的邊或頂點到自身的邊則叫簡單圖。
1)不存在重復邊
2)不存在頂點到自身的邊
所以上面的有向圖和無向圖都是簡單圖。與簡單圖相對的是多重圖,即:兩個結點直接邊數多于一條,又允許頂點通過同一條邊與自己關聯。
完全圖
無向圖中任意兩點之間都存在邊,稱為無向完全圖;
有向圖中任意兩點之間都存在方向向反的兩條弧,稱為有向完全圖
完全有向圖:有n個頂點的有向圖有n(n-1)條邊, 則此圖為完全有向圖。
子圖
若有兩個圖G=(V,E),G1=(V1,E2),若V1是V的子集且E2是E的子集,稱G1是G的子圖。
連通、連通圖、連通分量
1.連通
在無向圖中,兩頂點有路徑存在,就稱為連通的。
2.連通圖
若圖中任意兩頂點都連通,同此圖為連通圖。
如果對于任意兩個頂點都是連通的,則稱該圖是連通圖。
對于有向圖,如果圖中每一對頂點Vi和Vj是雙向連通的,則該圖是強連通圖。
連通:無向圖中每一對不同的頂點之間都有路徑。如果這個條件在有向圖里也成立,那么是強連通的。如果從頂點v到頂點v’有路徑或從頂點v’到頂點v有路徑,則稱頂點v和頂點v’是連通的。

有向圖的連通分支:將有向圖的方向忽略后,任何兩個頂點之間總是存在路徑,則該有向圖是弱連通的。有向圖的子圖是強連通的,且不包含在更大的連通子圖中,則可以稱為圖的強連通分支。
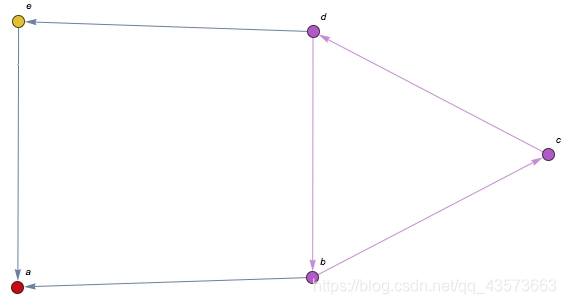
上圖, a 、e沒有到 { b , c , d } 中的頂點的路徑,所以各自是獨立的連通分支。因此,上圖有三個強連通分支,用集合寫出來就是: { { a } , { e } , { b , c , d } }
3.連通分量
無向圖中的極大連通子圖稱為連通分量。
雙連通圖:不含任何割點的圖。
邊的權和網
圖上的邊和弧上帶權則稱為網
圖中每條邊上標有某種含義的數值,該數值稱為該邊的權值。這種圖稱為帶樹圖,也稱作網。
加權圖
加權圖:與加權圖對應的就是無權圖,又叫等權圖。如果一張圖不含權重信息,我們認為邊與邊之間沒有差別。
鄰接和關聯
鄰接(adjacency):鄰接是兩個頂點之間的一種關系。如果圖包含 (u,v),則稱頂點v 與頂點u鄰接。在無向圖中,這也意味著頂點 u 與頂點 v 鄰接。
關聯(incidence):關聯是邊和頂點之間的關系。在有向圖中,邊 (u,v)從頂點 u開始關聯到 v,或者相反,從v關聯到u。在有向圖中,邊不一定是對稱的,有去無回是完全有可能的。
路徑
兩頂點之間的路徑指頂點之間經過的頂點序列,經過路徑上邊的數目稱為路徑長度。若有n個頂點,且邊數大于n-1,此圖一定有環。
路徑(path):依次遍歷頂點序列之間的邊所形成的軌跡。
樹中根節點到任意節點的路徑是唯一的,但是圖中頂點與頂點之間的路徑卻不是唯一的。
路徑的長度是路徑上的邊或弧的數目。
無權圖的路徑長是路徑包含的邊數。
有權圖的路徑長要乘以每條邊的權。
簡單路徑、簡單回路
簡單路徑:沒有重復頂點的路徑稱為簡單路徑。
除第一個頂點和最后一個頂點外,其余頂點不重復出現的回路稱為簡單回路。
環

環:包含相同的頂點兩次或者兩次以上。上圖序列 <1,2,4,3,1>,1出現了兩次,當然還有其它的環,比如<1,4,3,1>。
無環圖:沒有環的圖,其中,有向無環圖有特殊的名稱(DAG(Directed Acyline Graph)
頂點的度、入度和出度
頂點的度為以該頂點為一個端點的邊的數目。
對于無向圖,頂點的邊數為度,度數之和是頂點邊數的兩倍。
對于有向圖,入度是以頂點為終點,出度相反。有向圖的全部頂點入度之和等于出度之和且等于邊數。頂點的度等于入度與出度之和。
割點(關節點)
割點:如果移除某個頂點將使圖或者分支失去連通性,則稱該頂點為割點。某些特定的頂點對于保持圖或連通分支的連通性有特殊的重要意義。
割點的重要性不言而喻。如果你想要破壞互聯網,你就應該找到它的關節點。同樣,要防范敵人的攻擊,首要保護的也應該是關節點
橋(割邊)
橋(割邊):和割點類似,刪除一條邊,就產生比原圖更多的連通分支的子圖,這條邊就稱為割邊或者橋。
距離
若兩頂點存在路徑,其中最短路徑長度為距離。
有向樹
有一個頂點的入度為0,其余頂點的入度均為1的有向圖稱作有向樹。
圖的表示
鄰接列表
鄰接列表:在鄰接列表實現中,每一個頂點會存儲一個從它這里開始的邊的列表。比如,如果頂點A 有一條邊到B、C和D,那么A的列表中會有3條邊,鄰接列表只描述了指向外部的邊。A 有一條邊到B,但是B沒有邊到A,所以 A沒有出現在B的鄰接列表中。
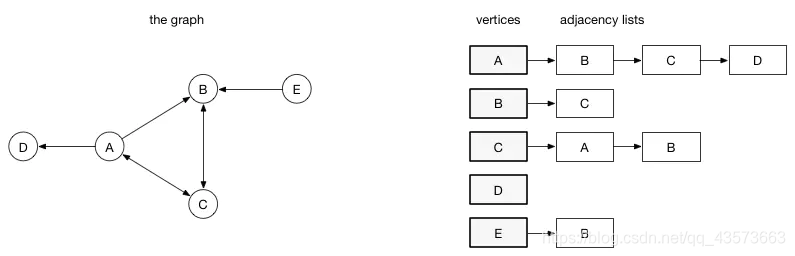
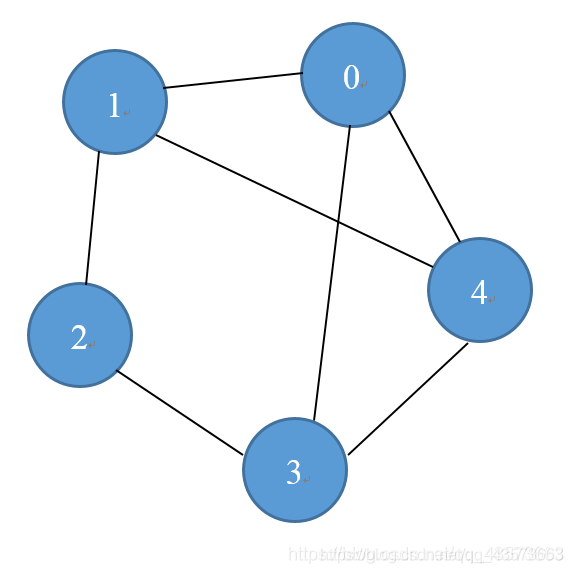
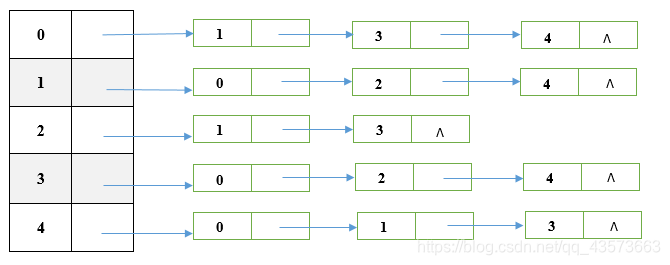
優點:
(1) 便于增加和刪除結點。
(2) 便于統計邊的數目,按頂點表順序掃描所有邊表可得到邊的數目,時間復雜度為O(n+e)。
(3)空間效率高。對于一個具有n個頂點e條邊的圖G,若圖G是無向圖,則在鄰接表表示中有n個頂點表結點和2n個邊表結點。若G是有向圖,則在它的鄰接表表示或逆鄰接表表示中均有n個頂點表結點和e個邊表結點。因此,鄰接表的空間復雜度為O(n+e)。
缺點:
(1) 不便于判斷頂點之間是否有邊,要判斷vi 和vj之間是否有邊,就需掃描第i個邊表,最換情況下要耗費O(n)時間。
(2) 不便于計算有向圖各個頂點的度。
鄰接矩陣
圖最常見的表示形式為鄰接鏈表和鄰接矩陣
特點:
⑴0表示這兩個頂點之間沒有邊,1表示有邊
⑵頂點的度是行內數組之和
⑶求頂點的鄰接點,遍歷行內元素即可
鄰接矩陣,一個存儲著邊的信息的矩陣,而頂點則用矩陣的下標表示。對于一個鄰接矩陣M,如果M(i,j)=1,則說明頂點i和頂點j之間存在一條邊,對于無向圖來說,M (j ,i) = M (i, j),所以其鄰接矩陣是一個對稱矩陣;對于有向圖來說,則未必是一個對稱矩陣。鄰接矩陣的對角線元素都為0。下圖是一個無向圖和對應的鄰接矩陣:
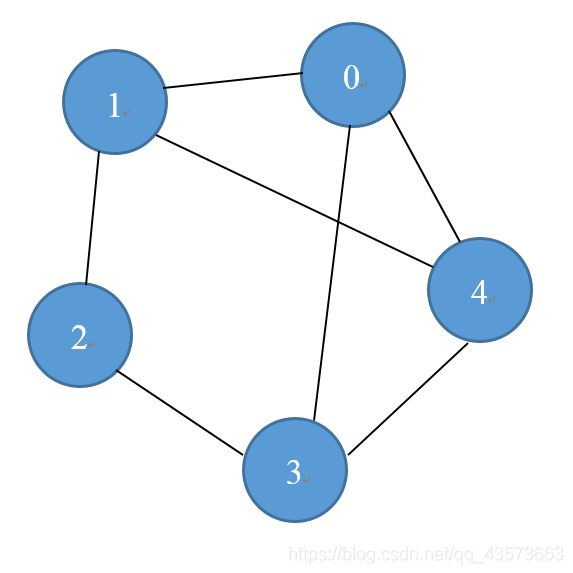

需要注意的是,當邊上有權值的時候,稱之為網圖,則鄰接矩陣中的元素不再僅是0和1了,鄰接矩陣M中的元素定義為:

鄰接矩陣:在鄰接矩陣實現中,由行和列都表示頂點,由兩個頂點所決定的矩陣對應元素表示這里兩個頂點是否相連、如果相連這個值表示的是相連邊的權重。例如,如果從頂點A到頂點B有一條權重為 5.6 的邊,那么矩陣中第A行第B列的位置的元素值應該是5.6:

優點:
(1) 便于判斷兩個頂點之間是否有 邊,即根據A[i][j] = 0或1來判斷。
(2) 便于計算各頂點的度。對于無向圖,鄰接矩陣的第i行元素之和就是頂點i的度。對于有向圖,第i行元素之和就是頂點i的出度,第i列元素之和就是頂點i的入度。
缺點:
(1) 不便于增加刪除頂點。
(2)空間復雜度高。如果是有向圖,n個頂點需要n*n個單元存儲邊。如果無向圖,其鄰接矩陣是對稱的,所以對規模較大的鄰接矩陣可以采用壓縮存儲的方法,僅存儲下三角元素,這樣需要n(n-1)/2個單元。無論哪種存儲方式,鄰接矩陣表示法的空間復雜度均為0(n*n)
區別:
鄰接列表在表示稀疏圖時非常緊湊而成為了通常的選擇,但稀疏圖表示時使用鄰接矩陣,會浪費很多內存空間,遍歷的時候也會增加開銷。
如果圖是稠密圖,可以選擇更加方便的鄰接矩陣。
還有,頂點之間有多種關系的時候,也不適合使用矩陣。因為表示的時候,矩陣中的每一個元素都會被當作一個表
圖的遍歷
深度優先遍歷
在深度優先搜索中,保存候補節點是棧,棧的性質就是先進后出,即最先進入該棧的候補節點就最后進行搜索。
深度優先遍歷,也有稱為深度優先搜索(Depth_First_Search),簡稱DFS。其實,就像是一棵樹的前序遍歷。
它從圖中某個結點v出發,訪問此頂點,然后從v的未被訪問的鄰接點出發深度優先遍歷圖,直至圖中所有和v有路徑相通的頂點都被訪問到。若圖中尚有頂點未被訪問,則另選圖中一個未曾被訪問的頂點作起始點,重復上述過程,直至圖中的所有頂點都被訪問到為止。
#include<iostream>
using namespace std;
int n,m,x,y,a[105][105],book[105][105]= {};
int minn = 999999;
void dfs(int starx,int stary,int step) {int nx,ny;if(starx==x&&stary==y) {if(minn > step) {minn = step;}return ;}int next[4][2]= {0,1,0,-1,1,0,-1,0};for(int i=0; i<4; i++) {nx = starx+next[i][0]; ny = stary+next[i][1];if(nx>n||nx<1||ny>m||ny<1)continue;if(a[nx][ny]==0&&book[nx][ny]==0) {book[nx][ny]=1;dfs(nx,ny,step+1);book[nx][ny]=0;}}return ;
}
int main() {cin>>n>>m>>x>>y;for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {cin>>a[i][j];}}book[1][1]=1;dfs(1,1,0);cout<<"最小值為=";cout<<minn<<endl;return 0;
}
/*
5 4 4 3
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
*/鄰接矩陣表達方式:
#define MAXVEX 100 //最大頂點數
typedef int Boolean; //Boolean 是布爾類型,其值是TRUE 或FALSE
Boolean visited[MAXVEX]; //訪問標志數組
#define TRUE 1
#define FALSE 0//鄰接矩陣的深度優先遞歸算法
void DFS(Graph g, int i)
{int j;visited[i] = TRUE;printf("%c ", g.vexs[i]); //打印頂點,也可以其他操作for(j = 0; j < g.numVertexes; j++){if(g.arc[i][j] == 1 && !visited[j]){DFS(g, j); //對為訪問的鄰接頂點遞歸調用}}
}//鄰接矩陣的深度遍歷操作
void DFSTraverse(Graph g)
{int i;for(i = 0; i < g.numVertexes; i++){visited[i] = FALSE; //初始化所有頂點狀態都是未訪問過狀態}for(i = 0; i < g.numVertexes; i++){if(!visited[i]) //對未訪問的頂點調用DFS,若是連通圖,只會執行一次{DFS(g,i);}}
}
鄰接表存儲結構:
//鄰接表的深度遞歸算法
void DFS(GraphList g, int i)
{EdgeNode *p;visited[i] = TRUE;printf("%c ", g->adjList[i].data); //打印頂點,也可以其他操作p = g->adjList[i].firstedge;while(p){if(!visited[p->adjvex]){DFS(g, p->adjvex); //對訪問的鄰接頂點遞歸調用}p = p->next;}
}//鄰接表的深度遍歷操作
void DFSTraverse(GraphList g)
{int i;for(i = 0; i < g.numVertexes; i++){visited[i] = FALSE;}for(i = 0; i < g.numVertexes; i++){if(!visited[i]){DFS(g, i);}}
}
對比兩個不同的存儲結構的深度優先遍歷算法,對于n個頂點e條邊的圖來說,鄰接矩陣由于是二維數組,要查找某個頂點的鄰接點需要訪問矩陣中的所有元素,因為需要O(n2)的時間。而鄰接表做存儲結構時,找鄰接點所需的時間取決于頂點和邊的數量,所以是O(n+e)。顯然對于點多邊少的稀疏圖來說,鄰接表結構使得算法在時間效率上大大提高。
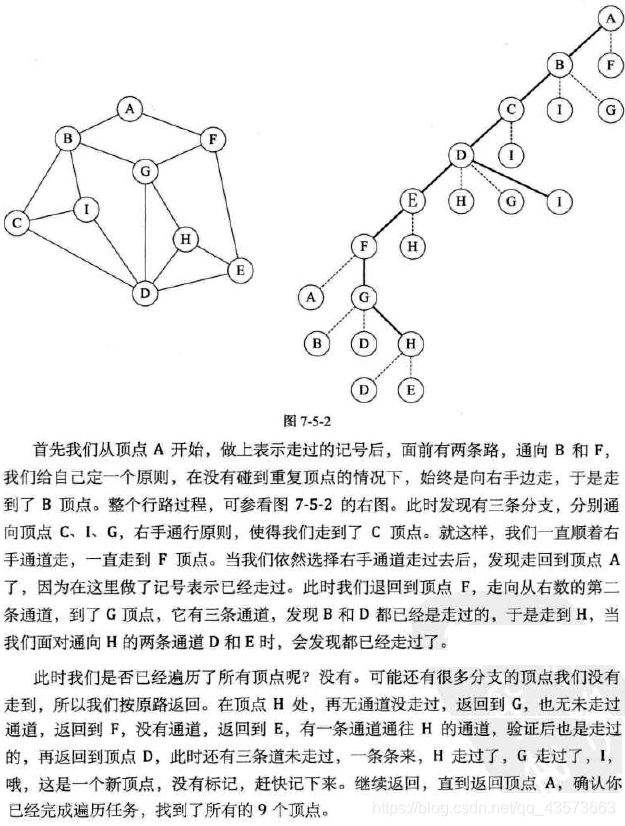
廣度優先遍歷
廣度優先搜索和深度優先搜索一樣,都是對圖進行搜索的算法,都是從起點開始順著邊搜索,此時并不知道圖的整體結構,直到找到指定節點(即終點)。在此過程中每走到一個節點,就會判斷一次它是否為終點。
廣度優先搜索會根據離起點的距離,按照從近到遠的順序對各節點進行搜索。而深度優先搜索會沿著一條路徑不斷往下搜索直到不能再繼續為止,然后再折返,開始搜索下一條路徑。
在廣度優先搜索中,有一個保存候補節點的隊列,隊列的性質就是先進先出,即先進入該隊列的候補節點就先進行搜索。
廣度優先搜索:將點存儲到隊列中
廣度優先遍歷(Breadth_First_Search),又稱為廣度優先搜索,簡稱BFS。
深度遍歷類似樹的前序遍歷,廣度優先遍歷類似于樹的層序遍歷。
鄰接矩陣的廣度遍歷算法:
void BFSTraverse(Graph g)
{int i, j;Queue q;for(i = 0; i < g.numVertexes; i++){visited[i] = FALSE;}InitQueue(&q);for(i = 0; i < g.numVertexes; i++)//對每個頂點做循環{if(!visited[i]) //若是未訪問過{visited[i] = TRUE;printf("%c ", g.vexs[i]); //打印結點,也可以其他操作EnQueue(&q, i); //將此結點入隊列while(!QueueEmpty(q)) //將隊中元素出隊列,賦值給{int m;DeQueue(&q, &m); for(j = 0; j < g.numVertexes; j++){//判斷其他頂點若與當前頂點存在邊且未訪問過if(g.arc[m][j] == 1 && !visited[j]){visited[j] = TRUE;printf("%c ", g.vexs[j]);EnQueue(&q, j);}}}}}
}
鄰接表的廣度優先遍歷:
void BFSTraverse(GraphList g)
{int i;EdgeNode *p;Queue q;for(i = 0; i < g.numVertexes; i++){visited[i] = FALSE;}InitQueue(&q);for(i = 0; i < g.numVertexes; i++){if(!visited[i]){visited[i] = TRUE;printf("%c ", g.adjList[i].data); //打印頂點,也可以其他操作EnQueue(&q, i);while(!QueueEmpty(q)){int m;DeQueue(&q, &m);p = g.adjList[m].firstedge; 找到當前頂點邊表鏈表頭指針while(p){if(!visited[p->adjvex]){visited[p->adjvex] = TRUE;printf("%c ", g.adjList[p->adjvex].data);EnQueue(&q, p->adjvex);}p = p->next;}}}}
}
對比圖的深度優先遍歷與廣度優先遍歷算法,會發現,它們在時間復雜度上是一樣的,不同之處僅僅在于對頂點的訪問順序不同。可見兩者在全圖遍歷上是沒有優劣之分的,只是不同的情況選擇不同的算法。

生成樹
生成樹的性質
一個有n個頂點的連通圖的生成樹有且僅有n-1條邊
一個連通圖的生成樹并不唯一
)


)


)
)






)

待更新)


