題目描述：

給定兩個字符串?text1?和?text2，返回這兩個字符串的最長?公共子序列?的長度。如果不存在?公共子序列?，返回?0?。

一個字符串的?子序列?是指這樣一個新的字符串：它是由原字符串在不改變字符的相對順序的情況下刪除某些字符（也可以不刪除任何字符）后組成的新字符串。

• 例如，"ace"?是?"abcde"?的子序列，但?"aec"?不是?"abcde"?的子序列。

兩個字符串的?公共子序列?是這兩個字符串所共同擁有的子序列。

示例 1：

輸入：text1 = "abcde", text2 = "ace" 
輸出：3  
解釋：最長公共子序列是 "ace" ，它的長度為 3 。

示例 2：

輸入：text1 = "abc", text2 = "abc"
輸出：3
解釋：最長公共子序列是 "abc" ，它的長度為 3 。

示例 3：

輸入：text1 = "abc", text2 = "def"
輸出：0
解釋：兩個字符串沒有公共子序列，返回 0 。

提示：

• 1 <= text1.length, text2.length <= 1000
• text1?和?text2?僅由小寫英文字符組成。

思路：

本題采用動態規劃的思想，是一道很經典的動態規劃問題，我們把查找公共子序列問題一步一步壓縮成最小子問題。創建dp表，寫出狀態轉移方程，本題難點在于如何求出狀態轉移方程。

首先，第一種情況當最后一個字符相同時，我們只要比較前n-1個字符，第二種情況，當最后一個字符不同時，我們將一個字符串的最后一位相前移動一個比較。

如圖：

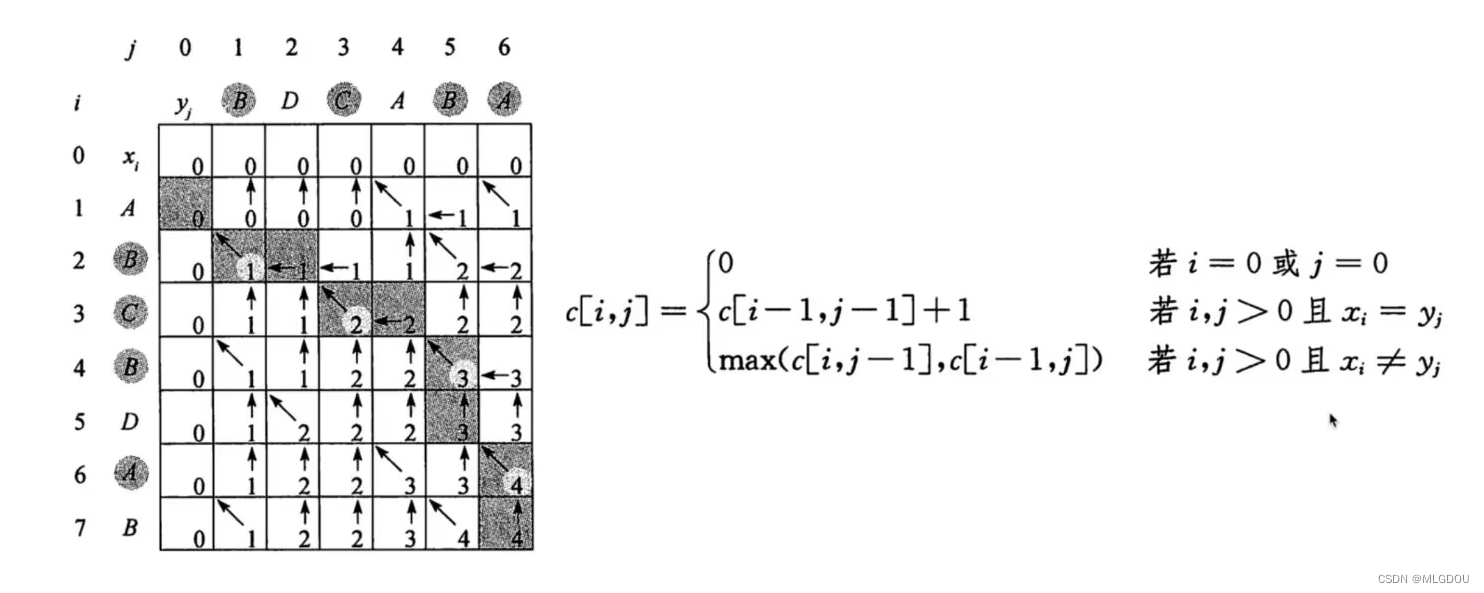
然后代碼實現時注意細節：我們dp表要創建的是m+1和n+1的大小，好進行初始化。

代碼實現

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m=text1.size();int n=text2.size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){if(text1[i-1]==text2[j-1])dp[i][j]=dp[i-1][j-1]+1;elsedp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};