k-means 和層次聚類都屬于劃分聚類,實際中最常用的是k-means,k-means效果不好的情況下才會采用其他聚類
K-means算法
K-means算法,也稱為K-平均或者K-均值,是一種使用廣泛的最基礎的聚類算法
假設輸入樣本為T=X1,X2,…,Xm;則算法步驟為(使用歐幾里得距離公式):
- Step1:隨機選擇初始化的k個類別中心a1,a2,…ak;
- Step2:對于每個樣本Xi,將其標記位距離類別中心aj最近的類別j
- 更新每個類別的中心點aj為隸屬該類別的所有樣本的均值,然后更新中心點
- 重復上面兩步操作,直到達到某個中止條件
中止條件:
迭代次數、最小平方誤差MSE(樣本到中心的距離平方和)、簇中心點變化率(結果相同)
算法執行過程圖:
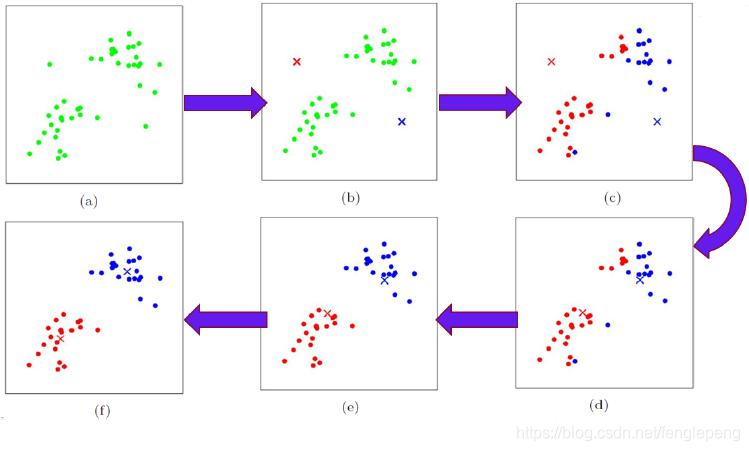
K-means算法:
記K個簇中心分別為???;每個簇的樣本數量為
;
使用平方誤差作為目標函數(使用歐幾里得距離),公式為:
要獲取最優解,也就是目標函數需要盡可能的小,對J函數求偏導數,可以得到簇中心點a更新的公式為:
K-means中的問題
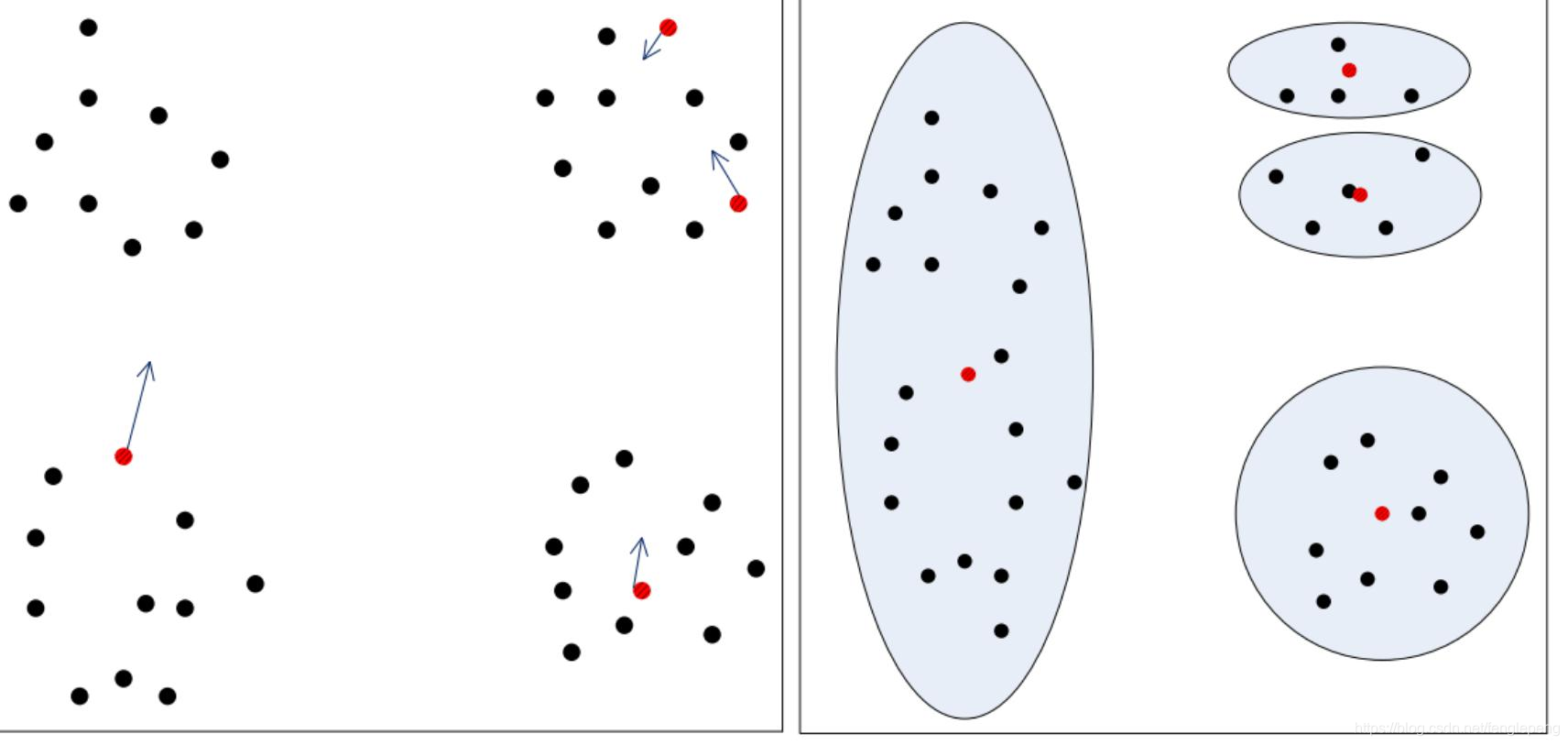
1、K-means算法在迭代的過程中使用所有點的均值作為新的質點(中心點),如果簇中存在異常點,將導致均值偏差比較嚴重
比如一個簇中有2、4、6、8、100五個數據,那么新的質點為24,顯然這個質點離絕大多數點都比較遠;在當前情況下,使用中位數6可能比使用均值的想法更好,使用中位數的聚類方式叫做K-Mediods聚類(K中值聚類)
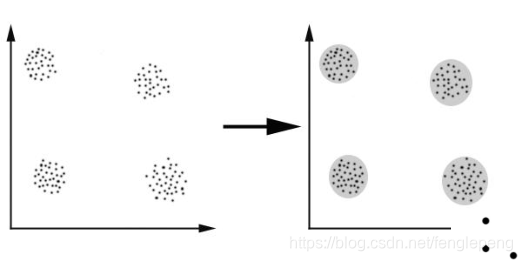
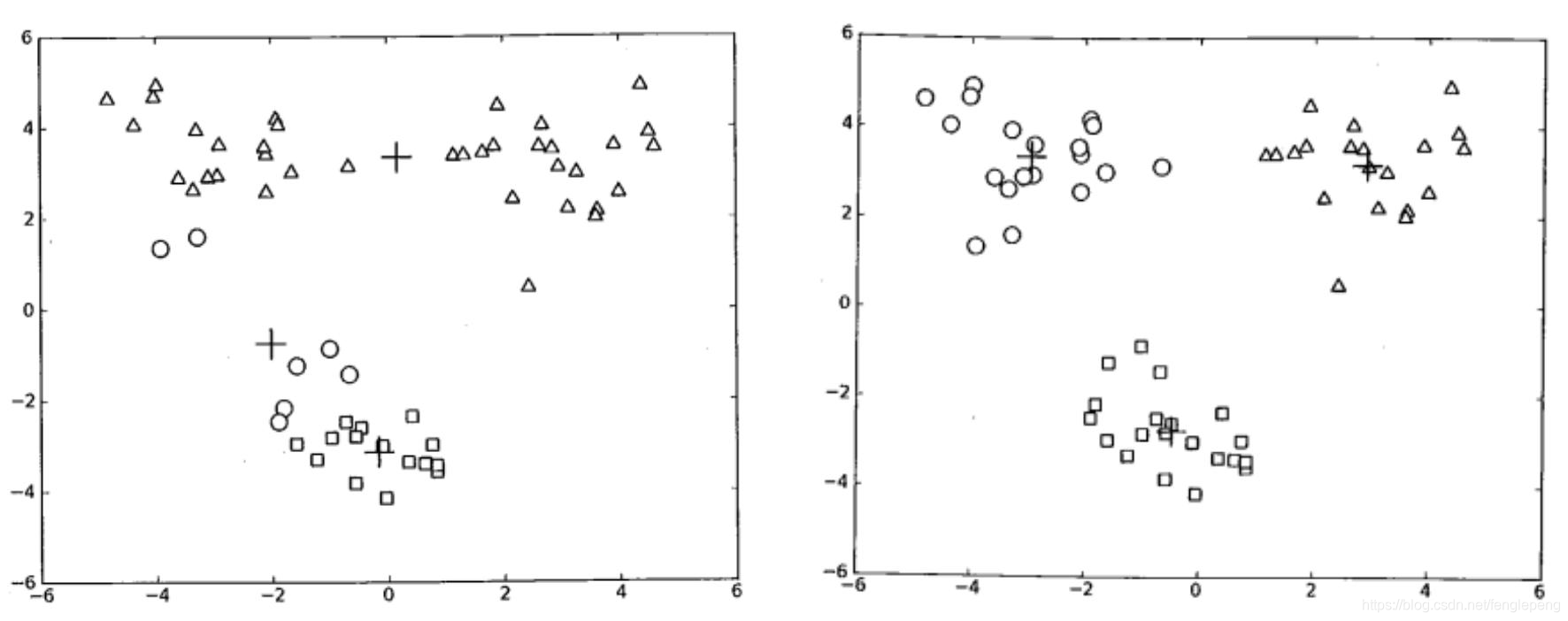
2、K-means算法是初值敏感(K值的給定和K個初始簇中心點的選擇)的,選擇不同的初始值可能導致不同的簇劃分規則
為了避免這種敏感性導致的最終結果異常性,可以采用初始化多套初始節點構造不同的分類規則,然后選擇最優的構造規則
K-means算法的初值敏感示意圖
K-means算法優缺點
缺點:
- K值是用戶給定的,在進行數據處理前,K值是未知的,不同的K值得到的結果也不一樣;
- 對初始簇中心點是敏感的
- 不適合發現非凸形狀的簇或者大小差別較大的簇
- 特殊值(離群值)對模型的影響比較大
優點:
- 理解容易,聚類效果不錯
- 處理大數據集的時候,該算法可以保證較好的伸縮性和高效率
- 當簇近似高斯分布的時候,效果非常不錯
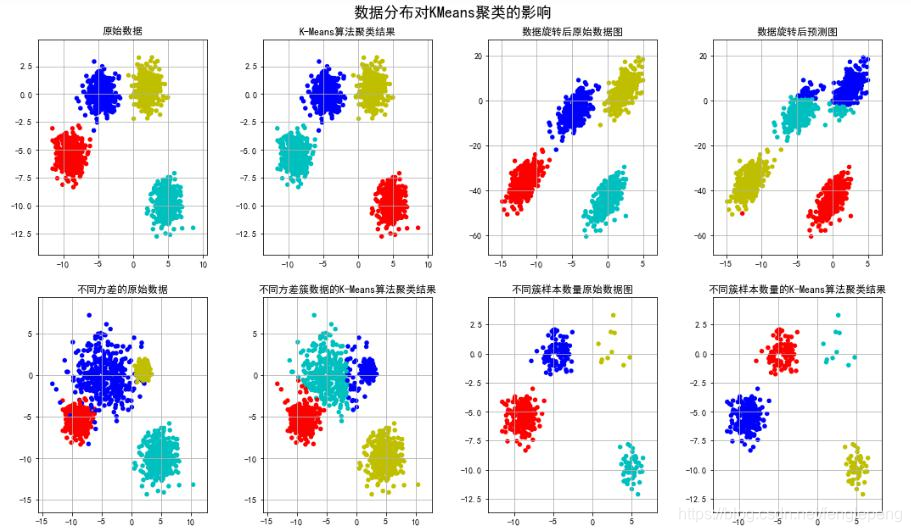
K-means案例
基于scikit包中的創建模擬數據的API創建聚類數據,使用K-means算法對數據進行分類操作,并獲得聚類中心點以及總的樣本簇中心點距離和值


二分K-Means
解決K-Means算法對初始簇心比較敏感的問題,二分K-Means算法是一種弱化初始質心的一種算法,具體思路步驟如下:
- 將所有樣本數據作為一個簇放到一個隊列中。
- 從隊列中選擇一個簇進行K-means算法劃分,劃分為兩個子簇,并將子簇添加到隊列中。
- 循環迭代第二步操作,直到中止條件達到(聚簇數量、最小平方誤差、迭代次數等)。
- 隊列中的簇就是最終的分類簇集合。
從隊列中選擇劃分聚簇的規則一般有兩種方式;分別如下:
- 對所有簇計算誤差和SSE(SSE也可以認為是距離函數的一種變種),選擇SSE最大的聚簇進行劃分操作(優選這種策略)。
- ?選擇樣本數據量最多的簇進行劃分操作。
K-Means++算法
解決K-Means算法對初始簇心比較敏感的問題,K-Means++算法和K-Means算法的區別主要在于初始的K個中心點的選擇方面,K-Means算法使用隨機給定的方式,K-Means++算法采用下列步驟給定K個初始質點:
- STEP1:從數據集中任選一個節點作為第一個聚類中心
- STEP2:對數據集中的每個點x,計算x到所有已有聚類中心點的距離和D(X),D(x)比較大的點作為下一個簇的中心。
- STEP3:重復2和3直到k個聚類中心被選出來
- STEP4:利用這k個初始的聚類中心來運行標準的k-means算法
缺點:由于聚類中心點選擇過程中的內在有序性,在擴展方面存在著性能方面的問題(第k個聚類中心點的選擇依賴前k-1個聚類中心點的值)
K-Means||算法
解決K-Means++算法缺點而產生的一種算法;主要思路是改變每次遍歷時候的取樣規則,并非按照K-Means++算法每次遍歷只獲取一個樣本,而是每次獲取K個樣本,重復該取樣操作O(logn)次,然后再將這些抽樣出來的樣本聚類出K個點,最后使用這K個點作為K-Means算法的初始聚簇中心點。實踐證明:一般5次重復采用就可以保證一個比較好的聚簇中心點。
Canopy算法
Canopy算法屬于一種“粗”聚類算法,執行速度較快,但精度較低,算法執行步驟如下:
- 給定樣本列表
以及先驗值?
??和?
- 從列表L中獲取一個節點P,計算P到所有聚簇中心點的距離(如果不存在聚簇中心,那么此時點P形成一個新的聚簇),并選擇出最小距離
- ?如果距離D小于
??,表示該節點屬于該聚簇,添加到該聚簇列表中
- 如果距離D小于
?,表示該節點不僅僅屬于該聚簇,還表示和當前聚簇中心點非常近,所以將該聚簇的中心點設置為該簇中所有樣本的中心點,并將P從列表L中刪除
- 如果距離D大于
,那么節點P形成一個新的聚簇,并將P從列表L中刪除
- 直到列表L中的元素數據不再有變化或者元素數量為0的時候,結束循環操作
Canopy算法得到的最終結果的值,聚簇之間是可能存在重疊的,但是不會存在某個對象不屬于任何聚簇的情況
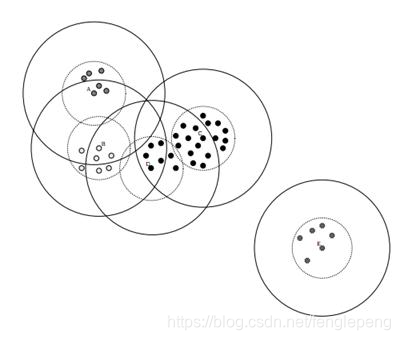
Canopy算法過程圖形說明
Canopy算法常用應用場景
由于K-Means算法存在初始聚簇中心點敏感的問題,常用使用Canopy+K-Means算法混合形式進行模型構建
先使用canopy算法進行“粗”聚類得到K個聚類中心點
K-Means算法使用Canopy算法得到的K個聚類中心點作為初始中心點,進行“細”聚類
優點:
- 執行速度快(先進行了一次聚簇中心點選擇的預處理)
- 不需要給定K值,應用場景多
- 能夠緩解K-Means算法對于初始聚類中心點敏感的問題
Mini Batch K-Means算法
Mini Batch K-Means算法是K-Means算法的一種優化變種,采用小規模的數據子集(每次訓練使用的數據集是在訓練算法的時候隨機抽取的數據子集)減少計算時間,同時試圖優化目標函數;Mini Batch K-Means算法可以減少K-Means算法的收斂時間,而且產生的結果效果只是略差于標準K-Means算法
算法步驟如下:
- 首先抽取部分數據集,使用K-Means算法構建出K個聚簇點的模型
- 繼續抽取訓練數據集中的部分數據集樣本數據,并將其添加到模型中,分配給距離最近的聚簇中心點
- 更新聚簇的中心點值(每次更新都只用抽取出來的部分數據集)
- 循環迭代第二步和第三步操作,直到中心點穩定或者達到迭代次數,停止計算操作
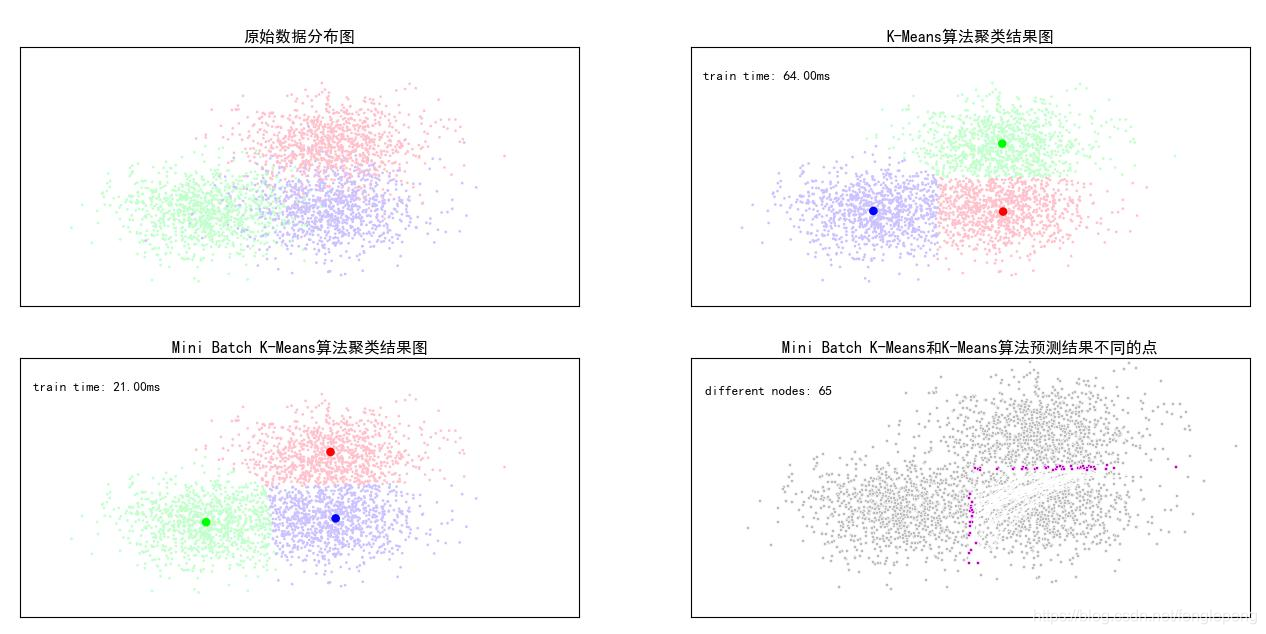
K-Means和Mini Batch K-Means算法比較案例
基于scikit包中的創建模擬數據的API創建聚類數據,使用K-means算法和MiniBatch K-Means算法對數據進行分類操作,比較這兩種算法的聚類效果以及聚類的消耗時間長度


聚類算法的衡量指標
均一性(類似正確率)
一個簇中只包含一個類別的樣本,則滿足均一性;其實也可以認為就是正確率(每個聚簇中正確分類的樣本數占該聚簇總樣本數的比例和)
完整性(類似召回率)
同類別樣本被歸類到相同簇中,則滿足完整性;每個聚簇中正確分類的樣本數占該類型的總樣本數比例的和。
V-measure均一性和完整性的加權平均
調整蘭德系數(ARI)
Rand index(蘭德指數)(RI),RI取值范圍為[0,1],值越大意味著聚類結果與真實情況越吻合。
其中C表示實際類別信息,K表示聚類結果,a表示在C與K中都是同類別的元素對數(也就是行),b表示在C與K中都是不同類別的元素對數(也就是列),表示數據集中可以組成的對數,即從樣本中取兩個.

調整蘭德系數(ARI,Adjusted Rnd Index),ARI取值范圍[-1,1],值越大,表示聚類結果和真實情況越吻合。從廣義的角度來將,ARI是衡量兩個數據分布的吻合程度的。
? ? E[RI]表示均值
調整互信息(AMI)
調整互信息(AMI,Adjusted Mutual Information),類似ARI,內部使用信息熵?? ?
?
S 表示整個數據集,U 表示整個預測的數據集,V?實際數據集(y值),C 表示原始的,R?表示預測的。一個樣本只屬于一個簇,所以?;一個樣本只能預測出一種結果,所以?
,
,表示實際和預測是相同的個數.
聚類算法的衡量指標-輪廓系數
簇內不相似度:計算樣本i到同簇其它樣本的平均距離為??;?
?越小,表示樣本i越應該被聚類到該簇,簇C中的所有樣本的?
?的均值被稱為簇C的簇不相似度。
簇間不相似度:計算樣本i到其它簇?? 的所有樣本的平均距離?
越大,表示樣本i越不屬于其它簇。
輪廓系數:??值越接近1表示樣本i聚類越合理,越接近-1,表示樣本i應該分類到另外的簇中,近似為0,表示樣本i應該在邊界上;所有樣本的?
的均值被稱為聚類結果的輪廓系數
?
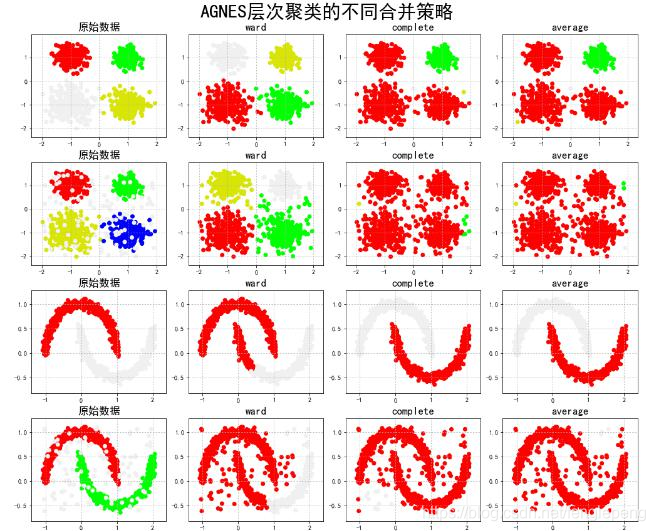
層次聚類方法
層次聚類方法對給定的數據集進行層次的分解或者合并,直到滿足某種條件為止,傳統的層次聚類算法主要分為兩大類算法:
凝聚的層次聚類:AGNES算法(AGglomerative NESting)—>采用自底向上的策略。最初將每個對象作為一個簇,然后這些簇根據某些準則被一步一步合并,兩個簇間的距離可以由這兩個不同簇中距離最近的數據點的相似度來確定,聚類的合并過程反復進行直到所有的對象滿足簇數目。
分裂的層次聚類:DIANA算法(DIvisive ANALysis)—>采用自頂向下的策略。首先將所有對象置于一個簇中,然后按照某種既定的規則逐漸細分為越來越小的簇(比如最大的歐式距離),直到達到某個終結條件(簇數目或者簇距離達到閾值)。
AGNES和DIANA算法優缺點
- 簡單,理解容易
- 合并點/分裂點選擇不太容易
- 合并/分裂的操作不能進行撤銷
- 大數據集不太適合(數據量大到內存中放不下)
- 執行效率較低O(t*n2),t為迭代次數,n為樣本點數
AGNES算法中簇間距離
最小距離(SL聚類)
? ? 兩個聚簇中最近的兩個樣本之間的距離(single/word-linkage聚類法)
? ? 最終得到模型容易形成鏈式結構
最大距離(CL聚類)
? ? 兩個聚簇中最遠的兩個樣本的距離(complete-linkage聚類法)
? ? 如果存在異常值,那么構建可能不太穩定
平均距離(AL聚類)
? ? 兩個聚簇中樣本間兩兩距離的平均值(average-linkage聚類法)
? ? 兩個聚簇中樣本間兩兩距離的中值(median-linkage聚類法)
層次聚類優化算法
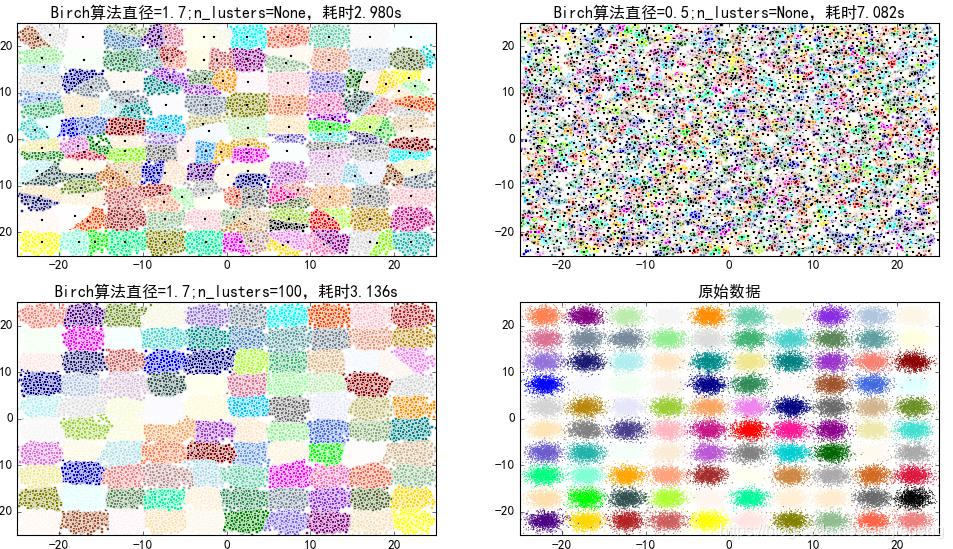
BIRCH算法(平衡迭代削減聚類法)(重要):聚類特征使用3元組進行一個簇的相關信息,通過構建滿足分枝因子和簇直徑限制的聚類特征樹來求聚類,聚類特征樹其實是一個具有兩個參數分枝因子和類直徑的高度平衡樹;分枝因子規定了樹的每個節點的子女的最多個數,而類直徑體現了對這一類點的距離范圍;非葉子節點為它子女的最大特征值;聚類特征樹的構建可以是動態過程的,可以隨時根據數據對模型進行更新操作。
優缺點:
- 適合大規模數據集,線性效率;
- 只適合分布呈凸形或者球形的數據集、需要給定聚類個數和簇之間的相關參數。
CURE算法(使用代表點的聚類法):該算法先把每個數據點看成一類,然后合并距離最近的類直至類個數為所要求的個數為止。但是和AGNES算法的區別是:取消了使用所有點或用中心點+距離來表示一個類,而是從每個類中抽取固定數量、分布較好的點作為此類的代表點,并將這些代表點乘以一個適當的收縮因子,使它們更加靠近類中心點。代表點的收縮特性可以調整模型可以匹配那些非球形的場景,而且收縮因子的使用可以減少噪音對聚類的影響。
優缺點:
- 能夠處理非球形分布的應用場景。
- 采用隨機抽樣和分區的方式可以提高算法的執行效率。
BRICH算法案例


密度聚類
密度聚類方法的指導思想: 只要樣本點的密度大于某個閾值,則將該樣本添加到最近的簇中。
這類算法可以克服基于距離的算法只能發現凸聚類的缺點,可以發現任意形狀的聚類,而且對噪聲數據不敏感。
計算復雜度高,計算量大。
常用算法:DBSCAN、密度最大值算法
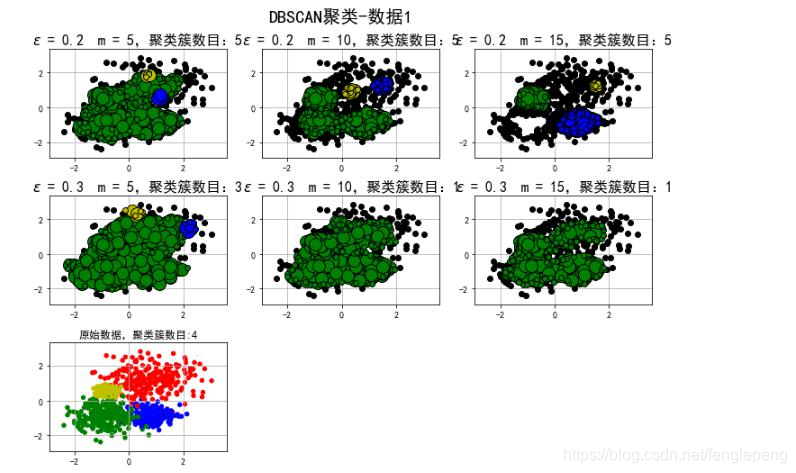
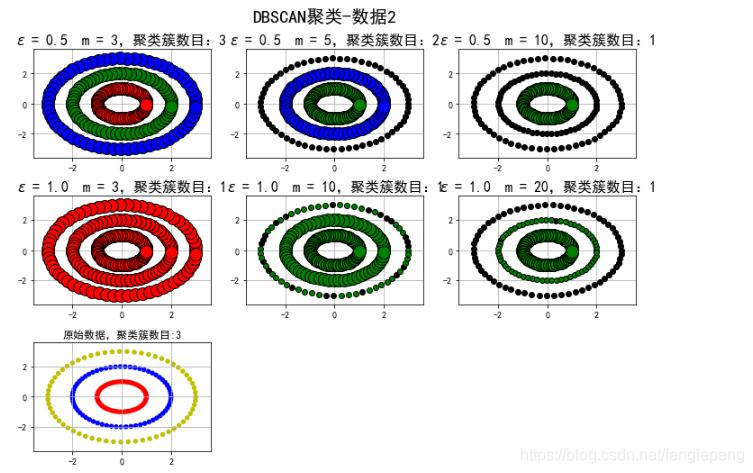
DBSCAN算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
一個比較有代表性的基于密度的聚類算法,相比于基于劃分的聚類方法和層次聚類方法,DBSCAN算法將簇定義為密度相連的點的最大集合,能夠將足夠高密度的區域劃分為簇,并且在具有噪聲的空間數據商能夠發現任意形狀的簇。
DBSCAN算法的核心思想是:用一個點的ε鄰域內的鄰居點數衡量該點所在空間的密度,該算法可以找出形狀不規則的cluster,而且聚類的時候事先不需要給定cluster的數量。
基本概念
ε鄰域(ε neighborhood,也稱為Eps):給定對象在半徑ε內的區域。
密度(density):ε鄰域中x的密度,是一個整數值,依賴于半徑ε。
MinPts定義核心點時的閾值,也簡記為M。
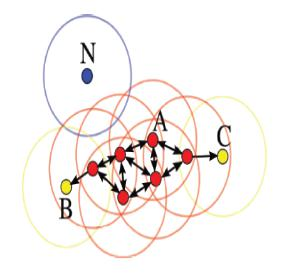
核心點(core point):如果 p(x)>=M ,那么稱 x 為 X 的核心點;記由X中所有核心點構成的集合為Xc,并記Xnc=X\Xc表示由X中所有非核心點構成的集合。直白來講,核心點對應于稠密區域內部的點。
邊界點(border point): 如果非核心點x的ε鄰域中存在核心點,那么認為x為X的邊界點。由X中所有的邊界點構成的集合為Xbd。邊界點對應稠密區域邊緣的點。
噪音點(noise point):集合中除了邊界點和核心點之外的點都是噪音點,所有噪音點組成的集合叫做Xnoi;,噪音點對應稀疏區域的點。
直接密度可達(directly density-reachable):給定一個對象集合X,如果y是在x的ε鄰域內,而且x是一個核心對象,可以說對象y從對象x出發是直接密度可達的。
密度可達(density-reachable):如果存在一個對象鏈p1,p2…pm,如果滿足pi+1是從pi直接密度可達的,那么稱p1是從p1密度可達的。
密度相連(density-connected):在集合X中,如果存在一個對象o,使得對象x和y是從o關于ε和m密度可達的,那么對象x和y是關于ε和m密度相連的。
簇(cluster):一個基于密度的簇是最大的密度相連對象的集合C;滿足以下兩個條件:
- Maximality:若x屬于C,而且y是從x密度可達的,那么y也屬于C。
- Connectivity:若x屬于C,y也屬于C,則x和y是密度相連的。
算法流程
- 如果一個點x的ε鄰域包含多余m個對象,則創建一個x作為核心對象的新簇;
- 尋找并合并核心對象直接密度可達的對象;
- 沒有新點可以更新簇的時候,算法結束。
算法特征描述:
- 每個簇至少包含一個核心對象。
- 非核心對象可以是簇的一部分,構成簇的邊緣。
- ·包含過少對象的簇被認為是噪聲。
DBSCAN算法總結
優點:
- 不需要事先給定cluster的數目
- 可以發現任意形狀的cluster
- 能夠找出數據中的噪音,且對噪音不敏感
- 算法只需要兩個輸入參數
- 聚類結果幾乎不依賴節點的遍歷順序
缺點:
- DBSCAN算法聚類效果依賴距離公式的選取,最常用的距離公式為歐幾里得距離。但是對于高維數據,由于維數太多,距離的度量已變得不是那么重要。
- DBSCAN算法不適合數據集中密度差異很小的情況。
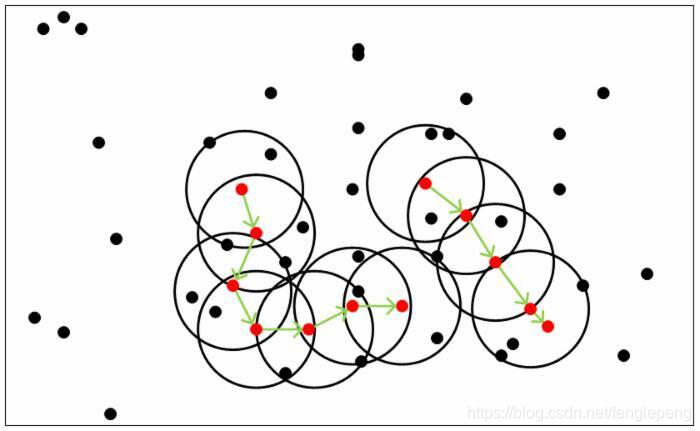
密度最大值聚類算法(MDCA)
MDCA(Maximum Density Clustering Application)算法基于密度的思想引入劃分聚類中,使用密度而不是初始點作為考察簇歸屬情況的依據,能夠自動確定簇數量并發現任意形狀的簇;另外MDCA一般不保留噪聲,因此也避免了閾值選擇不當情況下造成的對象丟棄情況。
MDCA算法的基本思路是尋找最高密度的對象和它所在的稠密區域;MDCA算法在原理上來講,和密度的定義沒有關系,采用任意一種密度定義公式均可,一般情況下采用DBSCAN算法中的密度定義方式。
MDCA相關概念
最大密度點: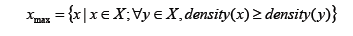
有序序列: 根據所有對象與pmax的距離對數據重新排序: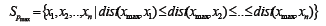
密度閾值density0;當節點的密度值大于密度閾值的時候,認為該節點屬于一個比較固定的簇,在第一次構建基本簇的時候,就將這些節點添加到對應簇中,如果小于這個值的時候,暫時認為該節點為噪聲節點。
簇間距離:對于兩個簇C1和C2之間的距離,采用兩個簇中最近兩個節點之間的距離作為簇間距離。
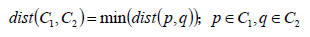
聚簇距離閾值dist0:當兩個簇的簇間距離小于給定閾值的時候,這兩個簇的結果數據會進行合并操作。
M值:初始簇中最多數據樣本個數。
算法流程
MDCA算法聚類過程步驟如下:
將數據集劃分為基本簇;
- 對數據集X選取最大密度點Pmax,形成以最大密度點為核心的新簇Ci,按照距離排序計算出序列Spmax,對序列的前M個樣本數據進行循環判斷,如果節點的密度大于等于density0,那么將當前節點添加Ci中;
- 循環處理剩下的數據集X,選擇最大密度點Pmax,并構建基本簇Ci+1,直到X中剩余的樣本數據的密度均小于density0。
使用凝聚層次聚類的思想,合并較近的基本簇,得到最終的簇劃分;
- 在所有簇中選擇距離最近的兩個簇進行合并,合并要求是:簇間距小于等于dist0,如果所有簇中沒有簇間距小于dist0的時候,結束合并操作
處理剩余節點,歸入最近的簇。
- 最常用、最簡單的方式是:將剩余樣本對象歸入到最近的簇。
密度聚類算法案例
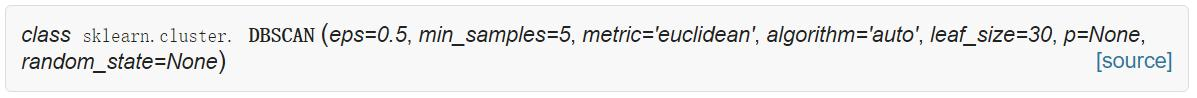
譜聚類
譜聚類是基于譜圖理論基礎上的一種聚類方法,與傳統的聚類方法相比:具有在任意形狀的樣本空間上聚類并且收斂于全局最優解的優點。
通過對樣本數據的拉普拉斯矩陣的特征向量進行聚類,從而達到對樣本數據進行聚類的目的;其本質是將聚類問題轉換為圖的最優劃分問題,是一種點對聚類算法。
譜聚類算法將數據集中的每個對象看做圖的頂點V,將頂點間的相似度量化為相應頂點連接邊E的權值w,這樣就構成了一個基于相似度的無向加權圖G(V,E),于是聚類問題就轉換為圖的劃分問題。基于圖的最優劃分規則就是子圖內的相似度最大,子圖間的相似度最小。
譜聚類的構建
譜聚類的構建過程主要包含以下幾個步驟:
- 構建表示對象相似度的矩陣W。
- 構建度矩陣D(對角矩陣)。
- 構建拉普拉斯矩陣L。
- 計算矩陣L的前k個特征值的特征向量(k個列向量)。
- 將k個列向量組成矩陣U。
- 對矩陣U中的n行數據利用K-means或其它經典聚類算法進行聚類得出最終結果。
應用場景及存在的問題
應用場景:圖形聚類、計算機視覺、非凸球形數據聚類等。
存在的問題:
- 相似度矩陣的構建問題:業界一般使用高斯相似函數或者k近鄰來作為相似度量,一般建議 使用k近鄰的方式來計算相似度權值。
- 聚類數目的給定。
- 如何選擇特征向量。
- 如何提高譜聚類的執行效率。
譜聚類應用案例

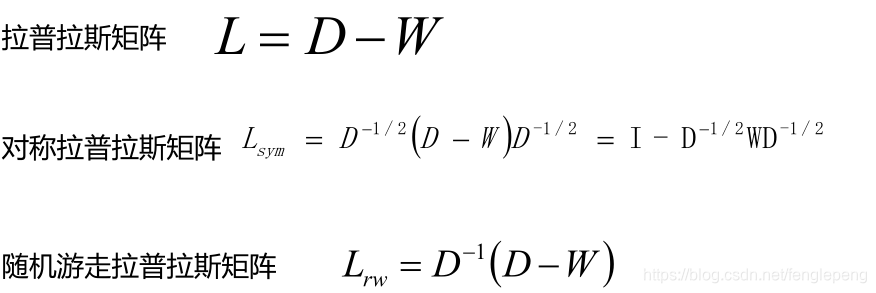




和坐標軸下降法(CD))










)



