又要考試了，推導一下方差最大化與均方差最小化，老師上課講了一些均方差最小化，推導的過程很詳細不過自己沒有記下來，復習的時候再推一遍加深印象。感謝 @耳東陳 老師的精彩課件！

一、方差的定義

去除均值，方便計算

將均值為0后，方差就可以表示成元素平方和除以個數，即

二、協方差的定義

由于均值為 0，所以我們的協方差公式可以表示為：

三、協方差矩陣

將和變量拼成一個矩陣

那么計算協方差矩陣

順便說一下,的期望也就是它與它自身的協方差，記為

四、方差最大化

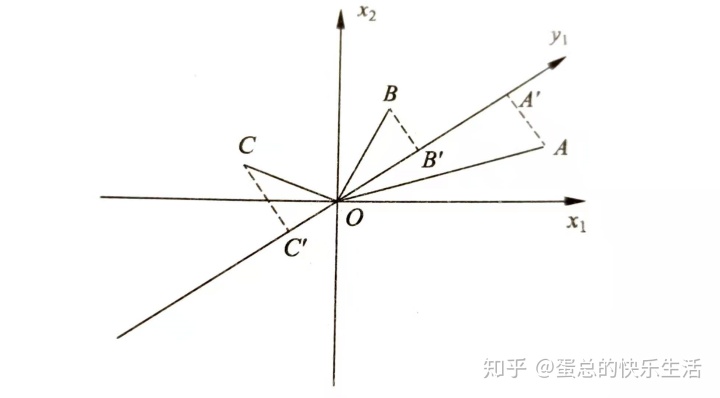
• 假設原來有兩個變量x1,x2,三個樣本點分別為ABC，樣本分布在由軸x1x2組成的坐標系中。
• 對坐標系進行旋轉變換，得到新的坐標軸y1，表示新的變量y1
• 樣本點ABC在y1軸上投影，得到軸的坐標值為
• 坐標軸的平方和
  為表示樣本在變量y1上的方差和
• 主成分分析旨在選取正交變換中方差最大的變量，作為第一主成分，也就是旋轉變換中坐標值平方和最大的軸
• 而我們知道，對于樣本而言，本身的
  為固有值，不變
• 因此可以通過勾股定理知道，方差最大
  最大等價于樣本點到軸的距離
  最小

基于PCA的線性結合的第一個主成分為

那么最大化方差為

而經過了去掉均值化后，期望為0

去均值化期望為0的具體步驟如下，假設為未去除均值的情況，均值為

那么回到(9)式，繼續計算這個方差，有兩種理解辦法，過程是一樣的

• 第一種根據方差與期望的關系，通過(10)(11)算式推得到從而最大化方差等價于最大化
• 第二種根據(2)的算式，期望為0，得到以下形式，結果是相同的

最后得到的最優化問題是

五、均方誤差最小化(MSE)

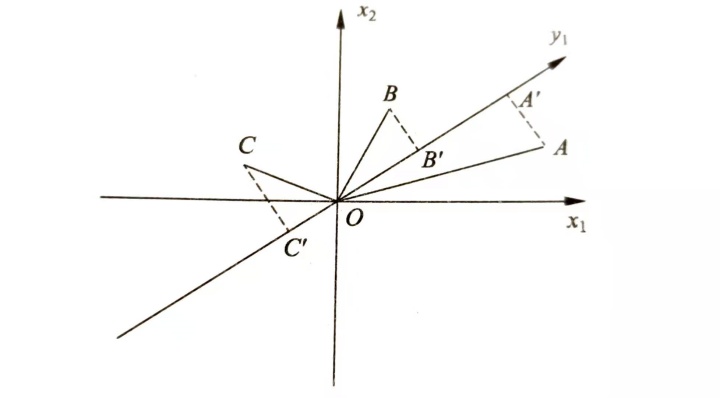
在方差最大化的圖中，(勾股定理)可以知道Variance+MSE=定值，因此二者是等價的，換一種思路通過均方誤差最小化進行推導。

向量的投影

以該圖的B點為例，設B點的坐標為x1,x2,其所代表的向量為

,由于

,那么可以同樣表示出直線的

,（注：由于該直線過原點就沒有寫截距項1）那么先算向量和向量的夾角

.

由于

,即

,可以繼續化簡為：

那么OB'的長度為

OB'的方向為

因此OB'的向量為

在這個部分，我們的目標是最小化均方誤差，也就是

下一步就是表示出

,由向量的知識，（方向換一下沒事，因為還要平方）可以得到

因此目標為

由于協方差

是定值，因此

越大，均方誤差越小。

即得到的最優化問題為：

六、求解最優化問題

根據拉格朗日方程：

那么對w求導可以得到

因此代入后有

即尋找最大的特征值即為所求。

那么從大到小排列

，便得到了各個主成分。

高維小樣本數據集的PCA方法預降維度方法及相關公式

• 例如:
• 這意味著在n很大的情況下，
  ，協方差矩陣太大并且不可逆很難分解
• 因此要采用預處理降維度的辦法