HDU 3572 Task Schedule

傳送門

作業調度，這道題還真沒想到能用網絡流。。。。乍一看跟背包問題差不多。
有N個作業，M個機器，每個作業給你一個耗費時間（時間段）以及最早開始時間和最晚完成時間（這兩個是時間點），單位是天。一個作業同時只能被一個機器做，一個機器同時也只能做一個作業，但是，可以只做一部分，之后可以切換別的機器做。一部分指的是整數天。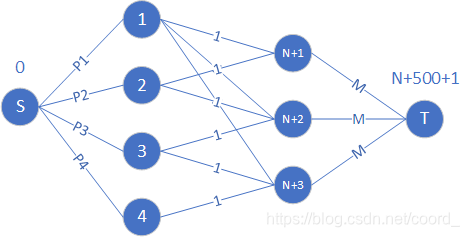

畫個圖。把數據處理成上面這個圖，然后按照最大流求解就ojbk了，看看最后的最大流是不是P1+P2+P3+...+PN（最大流必然小于等于這個，因為從源點輸出就這么些）
源點輸出到每個作業，權值等于這個作業的耗費時間P，代表你這個作業要處理P次（每次1天）；然后的N+1,N+2這些代表具體的某一天（整體上不一定連續每天都有，要根據每個作業的上下限來定），比如第一個作業的上下限是[N+1,N+3]，那么就把這個作業和這個上下限內的每一天都連上一條邊，權值是1（此時不用關心這個作業的花費時間，因為前面從源點連的邊已限制這一點），權值是1表示某一天內只能處理這個作業1天的完成量（這不是廢話么）；然后，代表某一天的每個點都要和匯點連上一條權值為M的邊，代表這一天最多能同時處理M個作業（因為機器只有M個）。
這個圖并不關心某個作業被具體哪些機器處理，因為這個不重要。只關心某個作業必須在哪些天內被處理，以及某一天最多同時處理多少個作業。

這個題還有個問題，就是他沒說清楚P<=E-S還是P<=E-S+1。這關系到在上面的圖中某個作業要連接E-S個點還是E-S+1個點。
當然，在樣例中的第二個輸出為Yes說明了是后者。但是真的夠sb的。

【19.3.18 想法】今天結合HDU 2883這個題，突然想到一個問題：該方法怎么保證某機器某一天一定處理某任務1天的工作量？而不是0.5個工作量？（也就是說從某任務點到某天數點的流量會不會大于0小于1？）
答案是不會的，因為P_N、M這些值都是整數且大于等于1，考慮最大流算法尋找增廣路的過程，權值為1的邊肯定是整條路上權值最小的邊，這條路的流量不可能比1再小了。

dinic

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <queue>
using namespace std;const int MAX = 500 + 500 + 2 + 10;
const int INF = 1e9;
int N, M, T;
int flow;
int sum;struct Edge
{int f, t, flow, cap;
};
vector<Edge> ve;
vector<int> v[MAX];int P, S, E;
bool vis[MAX];
int level[MAX];
int cur[MAX];void addEdge(int from, int to, int weight)
{ve.push_back(Edge{ from,to,0,weight });ve.push_back(Edge{ to,from,0,0 });v[from].push_back(ve.size() - 2);v[to].push_back(ve.size() - 1);
}void init()
{ve.clear();for (int i = 0; i <= N + 500 + 1; i++)v[i].clear();flow = sum = 0;memset(vis, 0, sizeof vis);
}bool bfs(int t)
{memset(level, -1, sizeof level);queue<int> q;q.push(0);level[0] = 0;for (; !q.empty();){int x = q.front();q.pop();for (int i = 0; i < v[x].size(); i++){Edge &e = ve[v[x][i]];if (level[e.t] < 0 && e.flow < e.cap){level[e.t] = level[x] + 1;q.push(e.t);}}}return level[t] >= 0;
}int dfs(int n, int t, int f)
{if(n == t || f == 0) return f;                   //for (int& i = cur[n]; i < v[n].size(); i++){Edge& e = ve[v[n][i]];int f0;if (level[e.t] == level[n] + 1 && (f0 = dfs(e.t, t, min(f, e.cap - e.flow))) > 0){e.flow += f0;ve[v[n][i] ^ 1].flow -= f0;return f0;}}return 0;
}int main()
{scanf("%d", &T);for (int cnt = 1; cnt <= T; cnt++){scanf("%d%d", &N, &M);init();for (int i = 1; i <= N; i++){scanf("%d%d%d", &P, &S, &E);if (P > E - S + 1)                      //{printf("Case %d: No\n\n", cnt);return 0;}addEdge(0, i, P);for (int j = S; j <= E; j++){addEdge(i, j + N, 1);//addEdge(j + N, 500 + N + 1, M);vis[j + N] = true;}sum += P;}for (int i = N + 1; i <= N + 500; i++)if (vis[i])addEdge(i, N + 500 + 1, M);for (; bfs(N + 500 + 1);){memset(cur, 0, sizeof cur);int temp;for (; temp = dfs(0, N + 500 + 1, INF);)flow += temp;//cout << flow;}printf("Case %d: %s\n\n", cnt, flow == sum ? "Yes" : "No");}return 0;
}