y,X1,X2,X3 分別表示第 t 年各項稅收收入(億元),某國生產總值GDP(億元),財政支出(億元)和商品零售價格指數(%).
(1) 建立線性模型: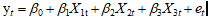
?① 自己編寫函數: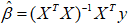
> library(openxlsx)
> data = read.xlsx("22_data.xlsx",sheet = 1)
> x = data[,-c(1,2)]
> x = cbind(rep(1,17),x)
> x_mat = as.matrix(x)
> y =matrix(data[,2],ncol = 1)
> res = solve(t(x_mat)%*%x_mat)%*%t(x_mat)%*%y
> res[,1]
rep(1, 17) 19412.8597818
X1 0.2679605
X2 -0.2874013
X3 -297.3653736
?所以各參數的估計值分別為?
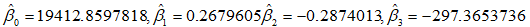
?② lm函數
> lm(y~x_mat)Call:
lm(formula = y ~ x_mat)Coefficients:(Intercept) x_matrep(1, 17) x_matX1
19412.859781545 NA 0.267960511 x_matX2 x_matX3 -0.287401287 -297.365373557
?于是各參數的估計值分別為

這兩個方法的結果是一樣的。
?
(2)要求實驗報告中畫出矩陣散點圖,給出參數的點估計、區間估計、t檢驗值、判定系數和模型F檢驗的方差分析表
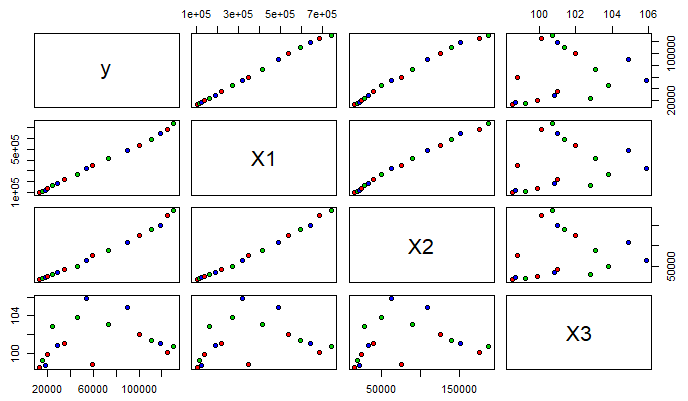
繪制矩陣散點圖。
library(graphics)
pairs(data[,-1]pch = 21,bg = c('red','green3','blue'))
# pch參數是控制點的形狀,bg是控制點的顏色
?
下面代碼給出參數的點估計,t檢驗值,判定系數
> summary(lm(y~x_mat+1))Call: lm(formula = y ~ x_mat + 1) #調用Residuals: #殘差統計量,殘差第一四分位數(1Q)和第三分位數(3Q)有大約相同的幅度,意味著有較對稱的鐘形分布Min 1Q Median 3Q Max -4397.9 -1102.4 153.8 1184.4 2934.6 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 1.941e+04 3.524e+04 0.551 0.591 x_matrep(1, 17) NA NA NA NA x_matX1 2.680e-01 4.466e-02 6.000 4.45e-05 *** x_matX2 -2.874e-01 1.668e-01 -1.723 0.109 x_matX3 -2.974e+02 3.688e+02 -0.806 0.435 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#標記為Estimate的列包含由最小二乘法計算出來的估計回歸系數。
#標記為Std.Error的列是估計的回歸系數的標準誤差。
#從理論上說,如果一個變量的系數是0,那么該變量將毫無貢獻。然而,這里顯示的系數只是估計,它們不會正好為0.
#因此,我們不禁會問:從統計的角度而言,真正的系數為0的可能性有多大?這是t統計量和P值的目的,在匯總中被標記為t value和Pr(>|t|) #P值估計系數不顯著的可能性,有較大P值的變量是可以從模型中移除的候選變量
Residual standard error: 2013 on 13 degrees of freedom Multiple R-squared: 0.9982, Adjusted R-squared: 0.9977 F-statistic: 2348 on 3 and 13 DF, p-value: < 2.2e-16
#Residual standard error 表示殘差的標準差,F-statistic 表示F的統計量
區間估計?方差分析表?
?
(3)保留模型中線性關系顯著的預測變量確定最后的模型,并利用R軟件中的"predict"語句預測2017年的稅收收入
?根據回歸分析結果,只有變量X1具有顯著性。所以模型中僅保留變量X1。
構造模型:
x_mat = cbind(rep(1,17),data[,3]) y = data[,2] res = lm(y~x_mat) res > resCall: lm(formula = y ~ x_mat)Coefficients: (Intercept) x_mat1 x_mat2 -6213.0189 NA 0.1915
?
?該模型為:Y = -6213.0189 + 0.1915 X1
接下來預測2017年的稅收收入,先根據數據data對 t 和 y 之間的關系進行回歸分析
t = data[,1] y = data[,2] res = lm(y~t) res> resCall: lm(formula = y ~ t)Coefficients: (Intercept) t -16428607 8213
?所以 t 與 y 的關系為:y? = -16428607 + 8213 t
?預測 2017 年的稅收收入:
> newdata = data.frame(t = 2017) > pre = predict(res,newdata,interval = "prediction",level = 0.95) > prefit lwr upr 1 136337.8 116018.1 156657.4
?



)














工具類,代碼高效復用)
