基于ECC算法的衍生算法

• ECDH(ECC+DH)
• RSA
• ECDHE(ECC+DHE)

ECDH密鑰協商（ECC+DH）

• 橢圓曲線密碼學是屬于非對稱密碼學的，其私鑰的計算公式如下：

1. 私鑰是一個隨機數d，取值范圍在1……n-1,其中n是子群的階
2. 公鑰是點H=dG，G是子群的基點

• 如果知道私鑰d 和橢圓曲線參數G，求公鑰H是很容易的，但是只知道公鑰H和橢圓曲線參數G，求解私鑰d是非常困難的，需要解決離散對數難題，橢圓曲線的安全性保證有賴于此。
• ECDH密鑰協商算法基于橢圓曲線密碼系統（ECC），使用較短的密鑰長度可提供與RSA或DH算法同等的安全等級，密鑰長度有160 ~ 256位比特的橢圓曲線算法與密鑰長度1024 ~ 3072位比特的非ECC算法安全強度相同。

常用有限域上的橢圓曲線

橢圓曲線由以下參數組成

T=(p,a,b,G,n,h)

• p 有限域中的大素數，長度一般224比特、256比特、384比特
• a 整數，橢圓方程系數
• b整數，橢圓方程系數
• G，橢圓曲線上某點，生成元
• n，為一個素數，表示橢圓曲線的階
• h，余因數
• 其中G包含Gx和Gy一共2個參數，非壓縮模式以04開始，壓縮模式以03開始，實際使用中一般采用非壓縮模式
• 通過模數p和系數a，b構成橢圓曲線方程y^2=x^3+ax+b mod p
• TLS支持很多橢圓曲線，常用的有2個secp256r1和secp284r1 : secp256r1大素數p長度256比特（32字節）和secp384r1大素數p長度384比特（48字節）

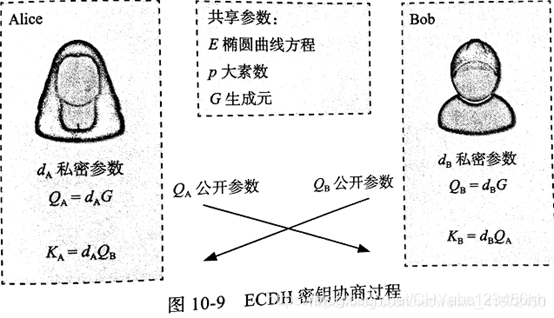
ECDH密鑰協商步驟

• ECDH其實和DH思想是一樣的，只不過這是基于橢圓曲線離散對數實現的。

ECDH共享參數

• Alice和Bob進行ECDH密鑰協商之前雙方要有共同的ECDH共享參數，即必須選擇相同的橢圓曲線方程、大素數p、生成源G，實際中這些橢圓曲線已經被相關組織批準，比如上邊的secp256r1和secp384r1，通過這個雙方就確定了這些共享參數

ECHD密鑰協商

1. Alice選擇一個比橢圓曲線階小的隨機數HA作為私密參數,計算公鑰HA=dAG發送給Bob
2. Bob選擇一個比橢圓曲線階小的隨機數HB作為私密參數,計算公鑰HB=dBG發送給Alice
3. Bob收到HA并計算得到共享密鑰參數S=dBHA
4. Alice收到HB并計算得到共享密鑰參數S=dAHB

• 根據橢圓曲線結合律S=dAHB=dAdBG=dBdAG=dBHA。目前Alice和Bob就得到了相同的S，但是第三方即使知道橢圓曲線和HA、HB的前提下，是無法獲取S的，因為在推導S的時候是需要知道其中一個私鑰，這必須破解橢圓曲線離散對數難題，這個是很難破解的。 應用上，一般先利用ECDH協商共享密鑰，再利用共享密鑰計算出對稱密鑰等其他需要的密鑰，通信雙發對數據進行對稱加密安全通信。

問題

• 如果采用靜態的 DH 算法和 ECC 結合就是 ECDH 算法。這種方式每次都使用的相同的 G 基點，它的優點在于可以避免每次在初始化連接時服務器頻繁生成 G。這個過程比較消耗 CPU。但是它帶來的缺點是，一旦隨機數 a、b 被泄露了，那么在這之前的所有會話都將會被解密。
• 為了解決這個問題，于是出現了 DHE 算法(Diffie-Hellman Ephemeral ，短暫臨時的 DH 算法)，結合 ECC 后形成了 ECDHE 算法。它可以保證每次通信使用的共享密鑰都是不同的，DH 密鑰對僅僅保存在內存中，不像 RSA 的私鑰保存在磁盤上，攻擊者即使從內存中破解了私鑰，也僅僅影響本次通信，所以無需擔心在此之前的通信內容會被解密，這樣的特征成為前向安全性(Forward Secrecy，FS)或者完全前向安全性(Perfect Forward Secrecy，PFS)。更安全的是，協商出會話密鑰后，a 和 b 兩個私鑰可以丟棄，進一步提升了安全性，在有限的時間、有效的空間生成了密鑰對。在 TLS 握手中使用的 ECDHE_ECDSA 和 ECDHE_RSA 密鑰交換算法。

如下圖

?

參考鏈接

• ECDH密鑰協商??https://blog.csdn.net/weixin_41572450/article/details/103207724
• ECDH密鑰交換?https://blog.csdn.net/s_lisheng/article/details/90712333