基本知識點

• 隨機試驗:1.不確定性2.可預知性3.可重復性
• 基本事件:包含一個樣本點
  必然事件:全集
  不可能事件:空集
  子集2^n-1-1(減去空集與真集)

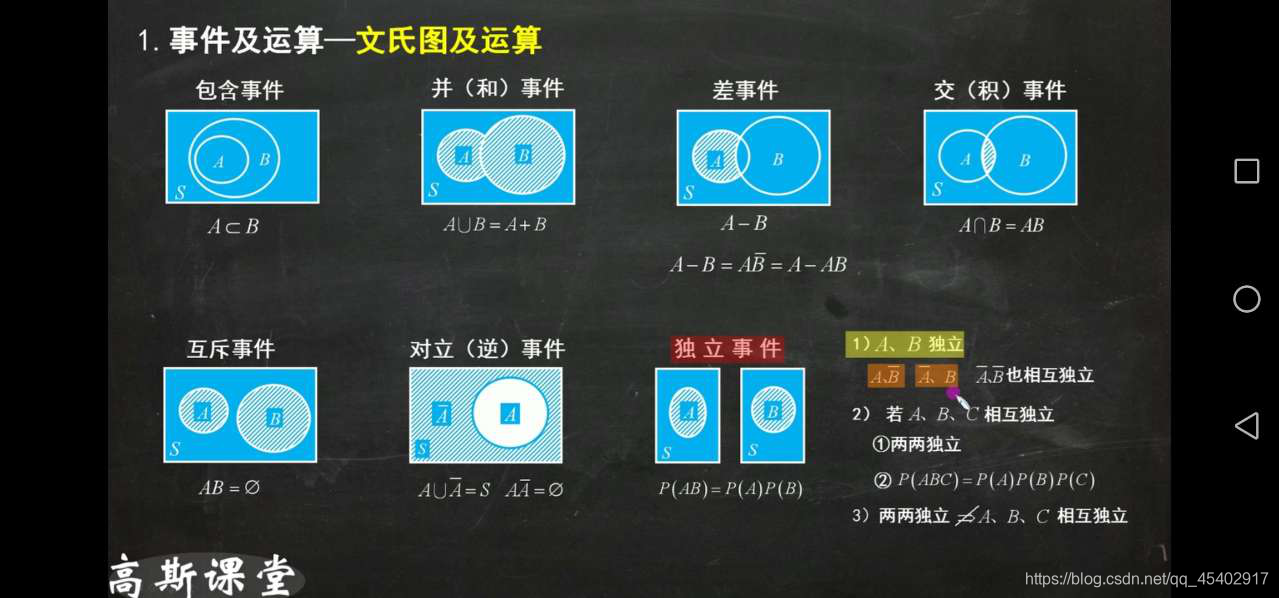
事件間的關系

1.包含關系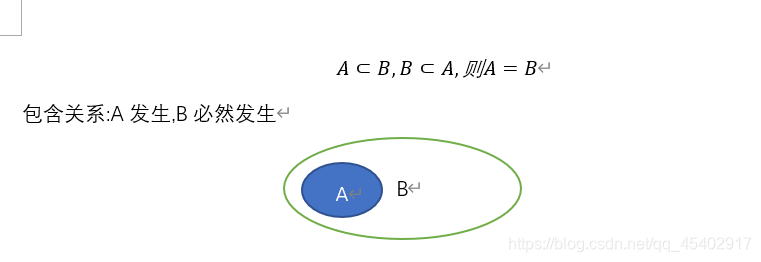
2.和運算AUB=A+B,A與B至少有一個發生
3.積事件A∩B=AB,AB同時發生
4.差事件A-B=AB ?=A-AB,A發生但B不發生
5.互不相容或互斥AB=?,兩個事件不能同時發生
6.對立事件或逆事件A+B=1,AB=?,其中必有一個發生的互斥事件
7.獨立事件:PAB=PA*PB

獨立事件

1.若A與B獨立,A與B-獨立,A-與B獨立,A-與B-獨立
2.兩個事件發生互不影響,PA|B=PA;PB|A=PB
3.A,B兩兩獨立不能保證A,B,C相互獨立

n重伯努利事件(二項分布)

只有兩個可能的結果:A發生或不發生,將這個試驗獨立地進行n次
p=Cn^kp^k
*(1-p)^n-k

公式與重點

1.常見逆事件
兩個事件至少有一個發生---->兩個事件都不發生

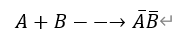
兩個事件同時發生—>至少有一個事件不發生

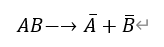
2.單調性

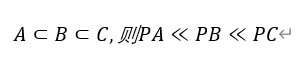
3.逆事件的概率

等可能概型(古典概型)

不放回抽樣

不放回抽樣是一種抽樣方法，它是在逐個抽取個體時，每次被抽到的個體不放回總體中參加下一次抽取的方法。采用不重復抽樣方法時，總體單位數在抽樣過程中逐漸減小，總體中各單位被抽中的概率先后不同。不放回抽樣也指整個樣本一次同時抽取的抽樣方法 .

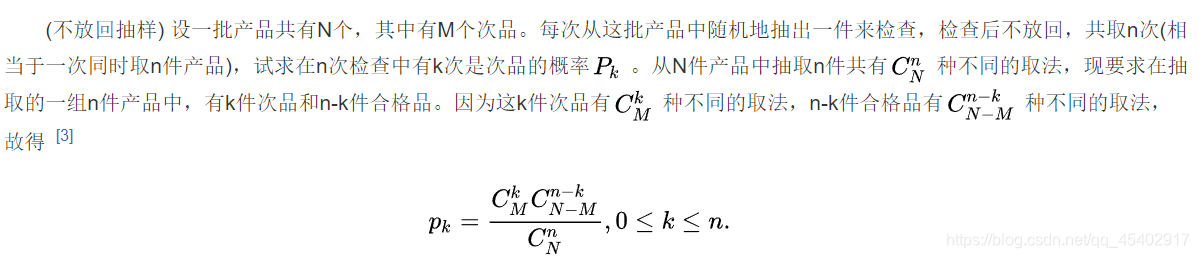
有放回抽樣

有放回抽樣是簡單隨機抽樣的操作方式之一。把總體中的抽樣單位從 1 至 N 編號， 每抽取一個號碼后再將它放回總體。對于任意一次抽取而言，由于總體容量不變，所以 N 個號碼被抽中的機會均等,1/n
抽獎:

幾何概型

常用計算知識點

1.一元二次方程的通式為：ax2+bx+c=0（a>0），并且判別式Δ=b2-4ac

2、若Δ＞0,一元二次方程有兩個不等實根

3、若Δ=0,一元二次方程有兩個相等實根，實際上就是一個實根

4、若Δ＜0,一元二次方程沒有實根

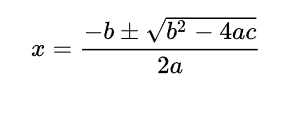
參考B站高斯課堂