---

容斥原理

容斥原理的簡介

容斥原理是組合數學中的一個重要原理，討論了滿足某些條件的元素個數問題。

對于 $n$ 個集合 $A_1,A_2,...A_n$，定義他們的并集包含的元素個數為 $|A_1\cup A_2\cup ...\cup A_n|$，那么根據容斥原理，有：

$|A_1\cup A_2\cup ?\cup A_n|$
$=|A_1|+|A_2|+?+|A_n|$
$?|A_1\cap A_2|???|A_{n?1}\cap A_n|$
$+|A_1\cap A_2\cap A_3|+?+(?1{)}^{n+1}|A_1\cap A_2\cap ?\cap A_n|$

（奇數項為正 偶數項為負）

例如：

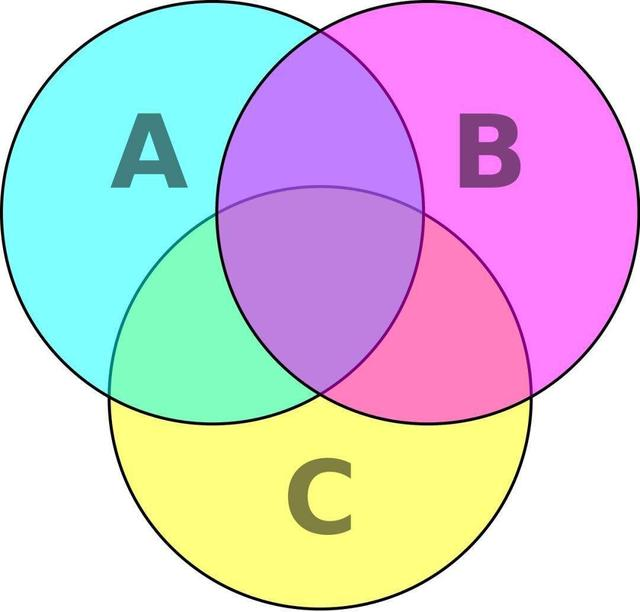
根據上圖可得
$|A\cup B\cup C|=|A|+|B|+|C|?|A\cap B|?|B\cap C|?|A\cap C|+|A\cap B\cap C|$

對于 $n$ 個集合 $A_1,A_2,...A_n$，其項數可以表示為 $C_n^1+C_n^2+?+C_n^n$ 通過數學計算可得 $C_n^1+C_n^2+?+C_n^n=2^n?1$，用此再乘以每項的時間復雜度便可以得到整體時間復雜度。

另外也可以通過數學計算得到 $C_n^1?C_n^2+?+(?1{)}^{n?1}{C}_n^n=1$。

能被整除的數（典型例題）

給定一個整數 $n$ 和 $m$ 個不同的質數 $p_1,p_2,\dots ,p_m$。

請你求出 $1$ ~ $n$ 中能被 $p_1,p_2,\dots ,p_m$ 中的至少一個數整除的整數有多少個。

輸入格式：
第一行包含整數 $n$ 和 $m$。

第二行包含 $m$ 個質數

輸出格式：
輸出一個整數，表示滿足條件的整數的個數。

數據范圍：
$1\le m\le 16$
$1\le n,p_i\le 10^9$

輸入樣例：

10 2
2 3

輸出樣例：

7

實現思路

計算 $1$ ~ $n$ 中能被 $p_i$ 一個數整除的整數的方法為 $?\frac{n}{p_i}?$。

由于不同質數間存在相同的可被整除的整數情況，這時候直接計算就會導致重疊部分計算多次，因此需要將重復的部分剔除出去，這里使用容斥原理來進行剔除操作。

計算 $1$ ~ $n$ 中能被 $p_i,p_j,p_k$ 多個數整除的整數（類似于重疊部分）的方法為 $?\frac{n}{p_i?p_j?p_k}?$。

將 $m$ 個質數看作 $m$ 個集合， 由于 $m$ 較小，我們可以使用int類型的二進制形式（32 bit）的變量來表示對每個集合的選取情況，1代表選用，0代表未選用。

比如：1110 可看作為選用集合 1 2 3，而集合 0 未選用，這樣便可以通過一個int類型遍歷來表示當前的集合選用情況。

通過二進制數模擬所有集合選用情況，再利用遍歷對二進制數進行解碼操作，而后進行正負性相加減便可以得到最終結果。

代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;const int N = 20;
int p[N];int main()
{int n, m, res = 0;cin >> n >> m;for (int i = 0; i < m; ++i) cin >> p[i];// 模擬對所有集合的每一種選用情況for (int i = 1; i < 1 << m; ++i) // 從1開始模擬{int t = 1, cnt = 0;for (int j = 0; j < m; ++j) // 將二進制數所表示的選用情況提取出來（解碼）{if (!(i >> j & 1)) continue;if ((long long)t * p[j] > n)// 當質數間的乘積大于n時，對應的質數重疊情況只有0個{t = -1;break;}t *= p[j];cnt++;}if (t != -1){int sign = (cnt & 1) ? 1 : -1; // 判斷奇偶性res = res + n / t * sign;}}cout << res << endl;return 0;
}

時間復雜度：$O(2^m?m)$

通過公式 $C_n^1+C_n^2+?+C_n^n=2^n?1$ 可得遍歷所有項的時間復雜度為 $O(2^m)$， 對單獨一項的時間復雜度為 $O(m)$，這是因為使用二進制數來表示情況，所以需要時間復雜度為 $O(m)$ 的遍歷來進行解碼操作，提取其中的選取信息。

擴展：用DPS實現

const int N = 20;
int n, m, p[N], res;// num-代表當前質數乘積 
// cur-代表指向質數數組的指針
// cnt-代表所選用集合的總數
void dfs(int num, int cur, int cnt)
{if (cur == m) // 當cur把質數數組都遍歷一遍之后代表該種選用情況的結束{if (cnt) // 排除一個質數都不選的選用情況{if (cnt % 2) res += n / num;else res -= n / num;}return;}dfs(num, cur + 1, cnt); // 不選用當前質數的集合dfs(num * p[cur], cur + 1, cnt + 1); // 選用當前質數的集合
}
int main()
{cin >> n >> m;for (int i = 0; i < m; ++i) cin >> p[i];dfs(1, 0, 0);cout << res << endl;return 0;
}

時間復雜度：$O(2^m)$

由于不用二進制數來模擬選取情況，所以也就不需要時間復雜度為 $O(m)$ 的遍歷來從二進制數中提取出選取情況的解碼操作。

博弈論

博弈論(Game Theory) 是研究 多方參與者 在某種競爭或合作情況下進行的策略選擇和相互作用的一門數學理論。它主要研究參與者如何通過各種策略最大化自己的收益。

博弈論中的相關性質

公平組合游戲(Impartial Combinatorial Game, ICG)是組合博弈論中的一個重要概念。

所謂公平組合游戲，是指具有以下特征：

1. 游戲中只有兩個玩家，分先手和后手。
2. 兩者地位完全對等，有同樣的可選行動。
3. 每個位置要么先手必勝，要么后手必勝，不存在平局。
4. 參與者都會采取最優策略。

注：城建棋類游戲，比如圍棋，就不是公平組合游戲。因為圍棋交戰雙方分別只能落黑子和白子，勝負判定也比較復雜，不符合公平組合游戲。

一些典型的公平組合游戲包括：

• Nim游戲：從幾堆物品中拿走任意數量的游戲。
• 威佐夫游戲：在圖上移動棋子吃掉對方的游戲。
• 沒有后效應的游戲：當前行動不會對之后可行動產生影響。

通過對這類游戲規律的研究，發展出了一套完整的理論體系，建立了組合博弈論這一獨立的學科分支。公平組合游戲抽象化地反映了很多現實世界的競爭情況。

博弈論的相關結論

先手必勝狀態：

• 在這個游戲狀態下，先手玩家有一個必勝策略，可以通過采取相應的游戲行動最終獲勝，不論對手如何行動。
• 即先手玩家可以保證自己贏得游戲。這個游戲狀態對先手玩家有利。

先手必敗狀態：

• 在這個游戲狀態下，先手玩家無論采取何種行動最終都會輸，后手玩家存在必勝策略。
• 即該狀態下無論先手玩家如何行動，后手玩家都可以通過相應的行動獲取最終的勝利。這個狀態對后手玩家有利。
• 后手玩家可以保證自己贏得游戲。

對于NIM游戲，在兩名選手都足夠聰明，每一步都是最優解的情況下：

$a_1\oplus a_2\oplus ?\oplus a_n=0$ 先手必敗

$a_1\oplus a_2\oplus ?\oplus a_n\ne 0$ 先手必勝

就是把所有堆的石子個數異或起來，結果是零，先手必敗，不是零，先手必勝。

先手必敗必勝的證明

①當 $a_1\oplus a_2\oplus ?\oplus a_n=0$ 時，先手必敗：

這個結論實際上是基于一個性質，即對于任意一個非負整數 $x$，有 $x\oplus x=0$。基于這個性質，我們可以證明在這種情況下，先手必敗。

假設初始狀態下，有 $a_1\oplus a_2\oplus ?\oplus a_n=0$。考慮以下情況：

• 如果先手選擇 $a_1$，那么剩下的異或和就變為 $(a_2\oplus ?\oplus a_n)$。
• 如果先手選擇 $a_2$，那么剩下的異或和就變為 $(a_1\oplus a_3\oplus ?\oplus a_n)$。
• 以此類推，如果先手選擇 $a_i$，剩下的異或和就變為 $(a_1\oplus ?\oplus a_{i?1}\oplus a_{i+1}\oplus ?\oplus a_n)$。

在這些情況下，無論先手如何選擇，剩下的異或和都會變成一個非零值。由于異或滿足交換律和結合律，這些選擇的結果最終都會導致剩余的異或和為一個非零值。因此，無論先手如何操作，最終的游戲狀態都會變為一個不滿足條件的狀態。

②當 $a_1\oplus a_2\oplus ?\oplus a_n\ne 0$ 時，先手必勝：

在這種情況下，異或和不為零。證明先手必勝需要使用歸納法。對于$n=1$的情況，只有一個數，先手直接取走即可。

假設對于 $n=k$，當 $a_1\oplus a_2\oplus ?\oplus a_k\ne 0$ 時，先手必勝。現在考慮 $n=k+1$ 的情況。

將 $a_1\oplus a_2\oplus ?\oplus a_{k+1}$ 分成兩部分：$x=a_1\oplus a_2\oplus ?\oplus a_k$ 和 $a_{k+1}$。根據歸納假設，當 $x\ne 0$ 時，先手必勝。此時，先手可以執行以下操作：

• 如果先手選擇取走 $a_{k+1}$，那么剩下的異或和變為 $x$，根據歸納假設，先手必勝。
• 如果先手選擇取走 $a_i$（$1\le i\le k$），剩下的異或和變為 $x\oplus a_i$。由于 $x\ne 0$，$x\oplus a_i$ 也不為零，那么根據歸納假設，先手也必勝。

因此，無論哪種情況，先手都有必勝策略。綜上所述，當 $a_1\oplus a_2\oplus ?\oplus a_n\ne 0$ 時，先手必勝。

Nim游戲（典型例題）

題目描述：
給定 $n$ 堆石子，兩位玩家輪流操作，每次操作可以從任意一堆石子中拿走任意數量的石子（可以拿完，但不能不拿），最后無法進行操作的人視為失敗。

問如果兩人都采用最優策略，先手是否必勝。

輸入格式：
第一行包含整數 $n$。

第二行包含 $n$ 個數字，其中第 $i$ 個數字表示第 $i$ 堆石子的數量。

輸出格式：
如果先手方必勝，則輸出 Yes。

否則，輸出 No。

數據范圍：
$1\le n\le 10^5,1\le$每堆石子數$\le 10^9$

輸入樣例：

2
2 3

輸出樣例：

Yes

代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;int main()
{int n, res = 0;cin >> n;for (int i = 0; i < n; ++i){int tmp;cin >> tmp;res ^= tmp;}if (res) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}

臺階-Nim游戲（典型例題）

題目描述：
現在，有一個 $n$ 級臺階的樓梯，每級臺階上都有若干個石子，其中第 $i$ 級臺階上有 $a_i$ 個石子（$i\ge 1$）。

兩位玩家輪流操作，每次操作可以從任意一級臺階上拿若干個石子放到下一級臺階中（不能不拿）。

已經拿到地面上的石子不能再拿，最后無法進行操作的人視為失敗。

問如果兩人都采用最優策略，先手是否必勝。

輸入格式：
第一行包含整數 $n$。

第二行包含 $n$ 個整數，其中第 $i$ 個整數表示第 $i$ 級臺階上的石子數 $a_i$。

輸出格式：
如果先手方必勝，則輸出 Yes。

否則，輸出 No。

數據范圍：
$1\le n\le 10^5,1\le a_i\le 10^9$

輸入樣例：

3
2 1 3

輸出樣例：

Yes

實現思路

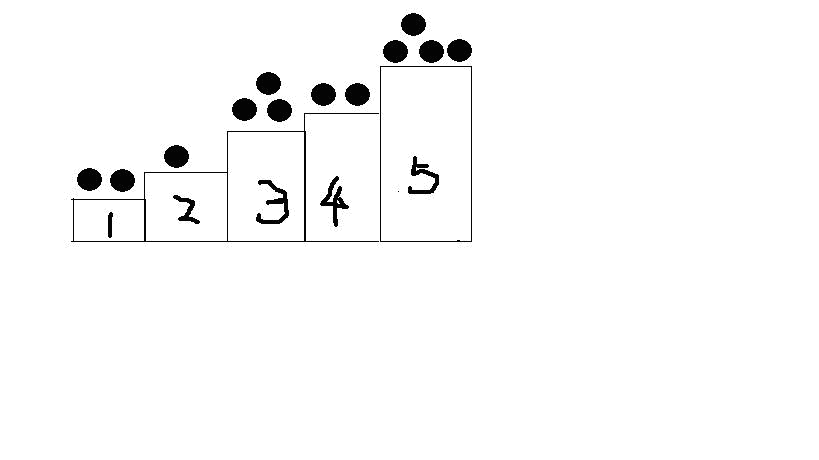
模擬每次只能向下挪動至下一級臺階的行動，我的想法是將高于臺階1的堆分成多個堆，例如圖中臺階5的堆，將這個堆分為5份石子數量相等的臺階1的堆，模擬需要至少5次才能將臺階5的堆拿至地面。

因此可以得到： $$\underset{臺階1}{\underbrace{2}}\oplus \underset{臺階2}{\underbrace{1\oplus 1}}\oplus \underset{臺階3}{\underbrace{3\oplus 3\oplus 3}}\oplus \underset{臺階4}{\underbrace{2\oplus 2\oplus 2\oplus 2}}\oplus \underset{臺階5}{\underbrace{4\oplus 4\oplus 4\oplus 4\oplus 4}}$$

由于異或(xor)的特性，相同的數異或等于0，便可以進行優化，當階數為偶數時，異或結果必定為0，奇數時，異或結果直接就等于臺階上的石子數。

從而可以推導出結論：

• 如果 奇數 階臺階的石子個數 異或值不是零，則 先手必勝。

• 如果 奇數 階臺階的石子個數 異或值是零， 則 先手必敗。

代碼實現

未利用異或特性優化前：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;int main()
{int n, res = 0;cin >> n;for (int i = 1; i <= n; ++i){int tmp, cnt = i;cin >> tmp;while (cnt--)	res ^= tmp; // 由臺階數分堆}if (res) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}

利用異或特性優化后：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;int main()
{int n, res = 0;cin >> n;for (int i = 1; i <= n; ++i){int tmp;cin >> tmp;if (i & 1) res ^= tmp; // 利用異或特性優化}if (res) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}

Mex函數與SG函數

有向圖游戲的概念：

• 節點和邊：有向圖游戲由一組節點和連接節點的有向邊組成。每個節點表示游戲的一個狀態，而有向邊表示從一個狀態到另一個狀態的合法轉移。

• 玩家輪流移動：在有向圖游戲中，玩家輪流進行移動。每一步玩家可以從當前狀態轉移到某個后繼狀態，選擇的后繼狀態必須遵循游戲的規則。

• 游戲終止狀態：每個有向圖游戲都有終止狀態，到達終止狀態后游戲結束。終止狀態可能是獲勝狀態或失敗狀態，這取決于游戲的規則。

• SG 函數和 Mex 函數：SG 函數（Sprague-Grundy 函數）和 Mex 函數是解決有向圖游戲的關鍵工具。SG 函數為每個節點賦予一個非負整數值，表示該節點的狀態價值。Mex 函數返回集合中沒有出現的最小非負整數。通過 SG 函數和 Mex 函數，可以計算出游戲的最佳策略。

• 必勝策略（先手必勝）和必敗策略（先手必敗）：在有向圖游戲中，存在必勝策略和必敗策略。如果一個玩家始終能夠采取最佳策略，并且可以確保在有限步內獲勝，那么該玩家有必勝策略。相反，如果玩家無論如何都無法避免失敗，那么該玩家有必敗策略。

• Nim 游戲和其他變體：Nim 游戲是有向圖游戲的一個著名例子，它涉及在堆中取石子。還有許多其他變體的有向圖游戲，如拈游戲、Grundy’s Game 等。

Mex(Minimum Excluded value)函數，是一個常見的組合游戲和集合論中的概念。它通常用來解決一類博弈問題，其中兩個玩家輪流從一個集合中取元素，每次取一個元素，并且不能重復取已經被取走的元素。當某一玩家無法繼續操作時，該玩家輸掉游戲。

Mex 函數的定義：對于一個給定的非負整數集合，它返回一個非負整數，表示在這個集合中，不屬于集合的最小非負整數。

mex ( S ) = min ? { x ∣ x ∈ N 0 , x ? S } \text{mex}(S) = \min \{ x \mid x \in \mathbb{N}_0, x \notin S \} mex(S)=min{x∣x∈N0?,x∈/S}

例如：

S = { 0 , 1 , 2 , 4 } ? m e x ( S ) = 3 S=\{0,1,2,4\} ? mex(S)=3 S={0,1,2,4}?mex(S)=3

$mex$函數和$sg$函數用于計算有向圖游戲的答案，主要思路是:

• $mex$函數返回集合 $S$ 中沒有出現的最小非負整數。
• $sg$函數定義為 $sg(n)=mex(sg(i_1),sg(i_2)...)$，其中 $i_1,i_2...$ 是節點 $n$ 的后繼節點。
• 對于圖 $G$，定義$sg(G)=sg(head)$，其中head是G的頭節點。
• 對于 $n$ 個圖 $G_1,G_2,...G_n$，它們的$sg$函數值的異或和就是這個有向圖游戲的答案。

假設有 $n$ 個獨立局面，它們的 $SG$ 值分別為 $sg(G1),sg(G2),...,sg(Gn)$，其中 $G_i$ 表示第 $i$ 個局面。那么整個組合游戲的 $SG$ 值 $sg(G)$ 可以表示為這些局面 $SG$ 值的異或和：

$$sg(G)=sg(G_1)\oplus sg(G_2)\oplus ...\oplus sg(G_n)$$

例如：

以NIM游戲為例，數量為7個石子的一堆，每人抽取輪流只能抽取2或5個石子，不能不抽取，判斷先手必勝還是先手必敗。

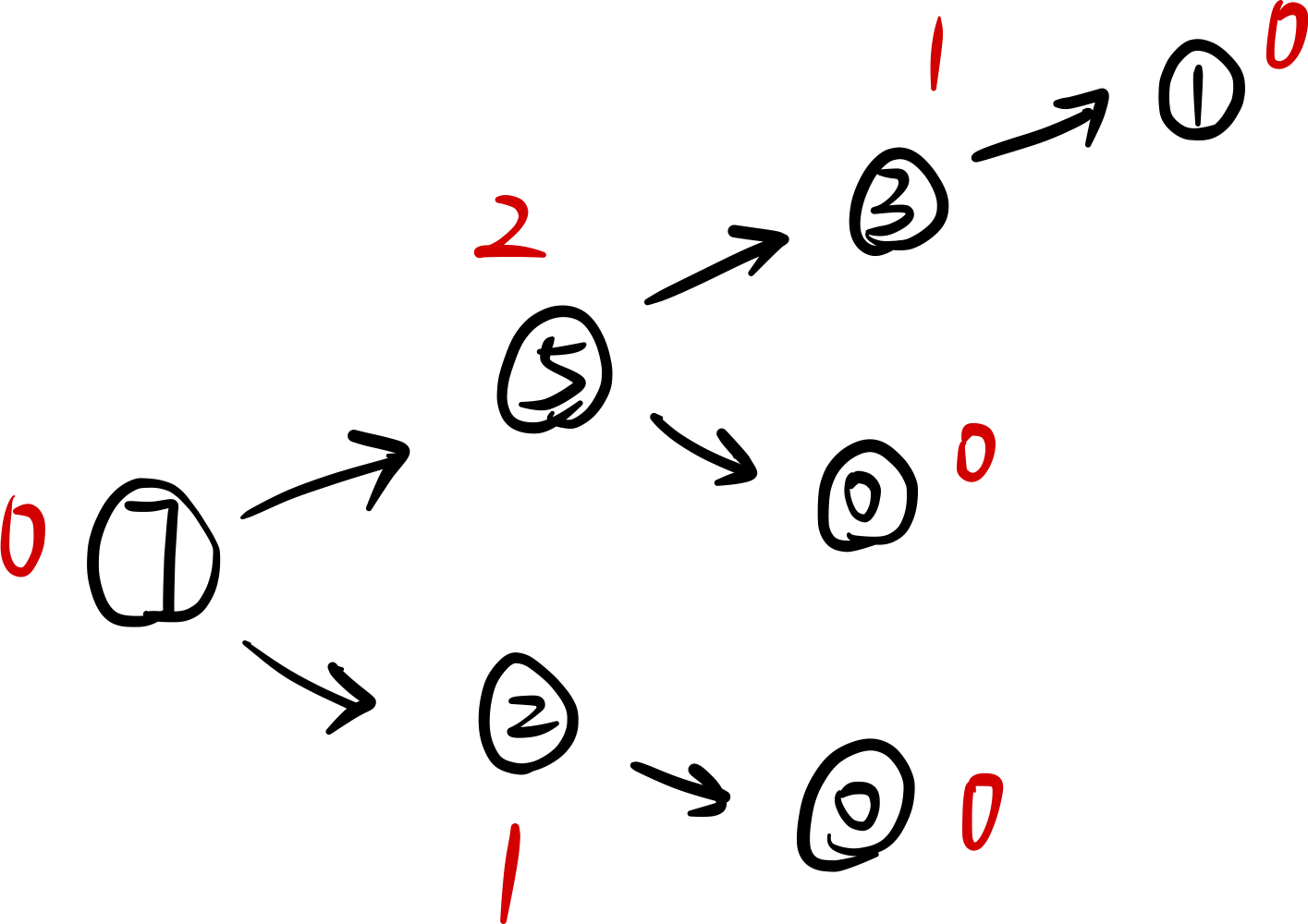
從末尾開始計算，可以得到$sg(head)=0$，由于此時只有一堆，即只存在一個有向圖，所以 $sg(head)=0$ 得到結果先手必敗。

對多個有向圖的情況（例如多個堆的情況），將每個有向圖的sg(head)異或到一起，再根據先手必勝必敗的條件，得出對應的結論。

對$G_1,G_2,G_3,\dots ,G_n$的 $n$ 個有向圖，結論為：

先手必敗：
$$sg(G_1)\oplus sg(G_2)\oplus sg(G_3)\oplus ?\oplus sg(G_n)=0$$
先手必勝：
$$sg(G_1)\oplus sg(G_2)\oplus sg(G_3)\oplus ?\oplus sg(G_n)\ne 0$$

集合-Nim游戲（典型例題）

題目描述：
給定 $n$ 堆石子以及一個由 $k$ 個不同正整數構成的數字集合 $S$。

現在有兩位玩家輪流操作，每次操作可以從任意一堆石子中拿取石子，每次拿取的石子數量必須包含于集合 $S$，最后無法進行操作的人視為失敗。

問如果兩人都采用最優策略，先手是否必勝。

輸入格式：
第一行包含整數 $k$，表示數字集合 $S$ 中數字的個數。

第二行包含 $k$ 個整數，其中第 $i$ 個整數表示數字集合 $S$ 中的第 $i$ 個數 $s_i$。

第三行包含整數 $n$。

第四行包含 $n$ 個整數，其中第 $i$ 個整數表示第 $i$ 堆石子的數量 $h_i$。

輸出格式：
如果先手方必勝，則輸出 Yes。

否則，輸出 No。

數據范圍：
$1\le n,k\le 100,1\le s_i,h_i\le 10000$

輸入樣例：

2
2 3

輸出樣例：

Yes

代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<unordered_set>
using namespace std;const int N = 110, M = 10010;
int a[N], f[M], k, n;int sg(int x)
{if (~f[x]) return f[x]; // 記憶化搜索：保證每種狀態只會被算一次unordered_set<int> s; // 用哈希表存儲當前節點的集合所存有的非負數的元素for (int i = 0; i < k; ++i){int num = a[i];if (x >= num) s.insert(sg(x - num)); // 將新的狀態加進來}for (int i = 0;; i++) if (!s.count(i)) return f[x] = i; // 找出不存在集合當中的最小值并返回
}
int main()
{int res = 0;memset(f, -1, sizeof f);cin >> k;for (int i = 0; i < k; ++i) cin >> a[i];cin >> n;for (int i = 0; i < n; ++i){int x;cin >> x;res ^= sg(x); // 求出每堆石子的SG值將其異或}if (res) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}

拆分-Nim游戲（典型例題）

題目描述：
給定 $n$ 堆石子，兩位玩家輪流操作，每次操作可以取走其中的一堆石子，然后放入兩堆 規模更小 的石子（新堆規模可以為 $0$，且兩個新堆的石子總數可以大于取走的那堆石子數），最后無法進行操作的人視為失敗。

問如果兩人都采用最優策略，先手是否必勝。

輸入格式：
第一行包含整數 $n$。

第二行包含 $n$ 個整數，其中第 $i$ 個整數表示第 $i$ 堆石子的數量 $a_i$。

輸出格式：
如果先手方必勝，則輸出 Yes。

否則，輸出 No。

數據范圍：
$1\le n,a_i\le 100$

輸入樣例：

2
2 3

輸出樣例：

Yes

實現思路

取走其中的一堆石子，然后放入兩堆 規模更小 的石子，相當于將一個局面拆分成了兩個局面，由SG函數理論：多個獨立局面的SG值，等于這些局面SG值的 異或和。

$$sg(G)=sg(G_1)\oplus sg(G_2)\oplus ...\oplus sg(G_n)$$

代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<unordered_set>
using namespace std;const int N = 110, M = 10010;
int f[N], n;int sg(int x)
{if (~f[x]) return f[x];unordered_set<int> s;for (int i = 0; i < x; ++i){for (int j = 0; j <= i; ++j)s.insert(sg(i) ^ sg(j));}for (int i = 0;; i++) if (!s.count(i)) return f[x] = i;
}
int main()
{memset(f, -1, sizeof f);cin >> n;int res = 0;while (n--){int x;cin >> x;res ^= sg(x);}if (res) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}